Dake L.P. Fundamentals of reservoir engineering

Подождите немного. Документ загружается.

IMMISCIBLE DISPLACEMENT 381

complex displacement problems using the assumption of segregated flow, these

include gravity drainage and bottom water coning.

In this section a great deal of attention has been focussed on the presentation of

approximate analytical methods for predicting oil recovery resulting from segregated

displacement. In reading the remainder of this chapter, however, the main point to

keep in mind is that the description of segregated flow in one dimension necessitates

the use of linear, averaged relative permeability functions, irrespective of whether the

displacement is stable or not. It is this fact which facilitated the derivation of such

simple recovery formulae.

10.7 ALLOWANCE FOR THE EFFECT OF A FINITE CAPILLARY TRANSITION ZONE IN

DISPLACEMENT CALCULATIONS

For the displacement of oil by water, exercises 10.2 and 10.3 clearly demonstrate the

sensitivity of the calculated oil recovery, as a function of time, to the assumed water

saturation distribution in the dip-normal direction. So far, too extreme notions of this

distribution have been considered; the uniform distribution (diffuse flow) and that due to

fluid segregation. From the information provided in the two exercises it is not possible

for the engineer to decide which, if either, of the assumed saturation distributions is

appropriate to describe the displacement. One vital piece of data has been omitted and

that is the capillary pressure curve and, in particular, the thickness of the capillary

transition zone.

If h is the reservoir thickness and H the thickness of the capillary transition zone then

the water saturation distribution can be approximated as uniform or segregated

depending on whether

H >> h (uniform)

H << h (segregated)

If the reservoir is very thin in comparison to the capillary transition zone the saturation

in the advancing water flood will appear to be uniformly distributed with respect to

thickness, fig. 10.7. On the other hand, if the transition zone is of negligible thickness

compared to the reservoir then it will appear that the oil and water are segregated.

Linear relative permeability curves can be used to describe such displacement.

The question then arises of how to describe oil displacement in a homogeneous

reservoir when the capillary transition zone is of the same order of magnitude as the

reservoir thickness (H ≈ h). Consider, for instance, the capillary pressure curve shown

in fig. 10.27(a) in which the capillary pressure difference across the transition zone is

3 psi.

IMMISCIBLE DISPLACEMENT 382

P (psi)

.2 .4

.6 .8 1.0

z (ft)

1.0

.2 .4

.6 .8 1.0

OIL

WATER

Fig. 10.27 (a) Imbibition capillary pressure curve, and (b) laboratory measured relative

permeabilities (rock curves,- table 10.1)

If oil displacement in the horizontal reservoir described in exercises 10.2 and 10.3 is re-

examined using this capillary pressure curve, then, since γ

= 1.04 and γ

= 0.81; the

capillary pressure versus capillary rise equation, (10.6), applied in the differential form

= .4335 ∆γ dz

gives the relationship

= .4335 (1.04−.81) dz = 0.1 dz (10.62)

Thus for dP

= 3 psi the height of the capillary transition zone is 30 ft which, since the

reservoir is 40 ft thick, means that neither diffuse nor segregated flow conditions can

be assumed to govern the displacement. Instead, it is necessary to generate averaged

relative permeability curves, which are functions of the thickness averaged water

saturation, and use these in the oil recovery calculations.

The manner in which this is done is illustrated graphically in fig. 10.28. Consider first of

all fig. 10.28(a). This represents the water saturation distribution, at any point in the

displacement path, as a function of thickness. For this initial case the maximum water

saturation, S

= 1−S

= 0), is assumed to be at the base of the reservoir, above

which the saturation is distributed in accordance with the saturation-capillary rise

function, fig. 10.27(a). Since the reservoir is homogeneous, the thickness averaged

water saturation can be expressed mathematically as

S(z)dz

(10.63)

IMMISCIBLE DISPLACEMENT 383

.2 .4

.6 .8 1.0

= .357

(ft)

.2 .4

.6 .8 1.0

= .047; k

= .481

(ft)

(z)

Fig. 10.28 (a) Water saturation, and (b) relative permeability distributions, with

respect to thickness when the saturation at the base of the reservoir is

= 1 −

−−

− S

=0)

which can be evaluated graphically by measuring the shaded area to the left and

beneath the saturation-thickness function, fig. 10.28(a), and dividing this by the total

height, h = 40 ft. For this initial saturation distribution S

= 0.357.

The rock relative permeabilities presented in table 10.1, which have been used in

exercises 10.2 and 10.3, are plotted as fig. 10.27(b). As already mentioned, these

represent point relative permeabilities in the reservoir and are dependent on the water

saturation at the point in question. Therefore, since there is a defined water saturation

distribution in the reservoir, fig. 10.28(a), there must also be a relative permeability

distribution, with respect to thickness, for both oil and water. These distributions can be

determined by selecting a particular height in the reservoir and reading the water

saturation at that point from fig. 10.28(a). For this saturation the corresponding point

relative permeabilities are read from fig. 10.27 (b). These relative permeability

distributions are listed in table 10.9 and plotted in fig. 10.28(b).

Mathematically, the thickness averaged relative permeabilities are

rw w

k(S(z))dz

k(S)

(10.64)

and

ro w

k(S(z))dz

k(S)

(10.65)

IMMISCIBLE DISPLACEMENT 384

fig.10.28(a)

fig.10.28(b)

0 .800 .300 0

5 .650 .170 .055

10 .470 .060 .195

15 .350 .020 .370

20 .275 .006 .540

25 .225 .002 .690

30 .200 0 .800

40 .200 0 .800

TABLE 10.9

Water saturation and point relative permeability distributions as functions

of the reservoir thickness; fig.10.28(a) and (b).

Graphically these values can be determined by measuring the area to the left of each

curve in fig. 10.28(b) and dividing by the total thickness. For this initial saturation

distribution,

k(S)= 0.047 and

k(S)= 0.481

After all this work all that has been obtained is one value of the thickness averaged

saturation

S and the corresponding values of thickness averaged water and oil

relative permeabilities

k(S) and

k(S). These three values are only relevant for

the initial assumption that the maximum water saturation has reached the base of the

reservoir at the point in question.

The next stage in generating averaged relative permeability curves is to allow the

maximum water saturation, S

= 1−S

, to rise by an arbitrary amount and recalculate

the new thickness averaged water saturation and relative permeabilities corresponding

to the new water saturation distribution. This process is illustrated in fig. 10.29 in which

the maximum water saturation is allowed to rise in 10 foot increments. Physically this

corresponds to a series of saturation distributions observed at a fixed point in the

reservoir as the flood passes that point. The main assumption which permits the

drawing of the saturation distributions, shown in fig.10.29 (a)−(h), is that of vertical

equilibrium described in sec. 10.2. This implies that as the average water saturation at

the point of observation increases, the water and oil are instantaneously distributed in

accordance with capillary-gravity equilibrium. Thus in fig. 10.29(a), above the height of

10 feet, the capillary pressure curve, fig. 10.27(a), is retraced to give the appropriate

water saturation distribution.

For each height rise of the saturation, S

= 1−S

, relative permeability distributions

have also been plotted in fig. 10.29 and in each case values of S

,k

and

k(S)have been calculated by graphical integration, as described previously. These

average values are listed in table 10.10 and plotted in fig. 10.30 as the circled points.

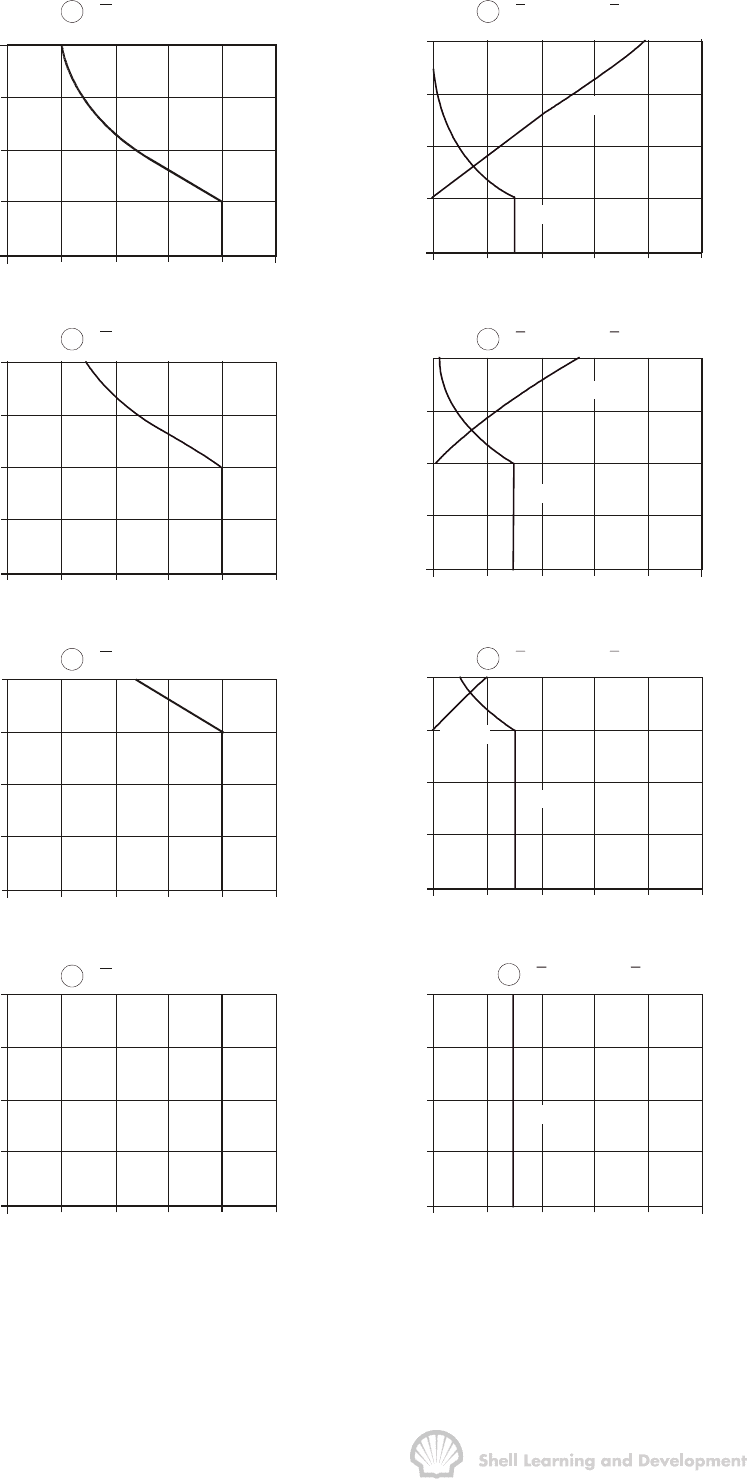
IMMISCIBLE DISPLACEMENT 385

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.

= .504

= .648

= .756

= .800

(ft)

= .130 ; k

= .280

rw ro

= .203 ; = .120

rw ro

= .300 ; = 0

k (z)

rw ro

= .269 ; = .025

k (z)

Fig. 10.29 Water saturation and relative permeability distributions, as functions of

thickness, as the maximum saturation, S

= 1 −

−−

− S

, is allowed to rise in 10

foot increments in the reservoir

IMMISCIBLE DISPLACEMENT 386

k(S)

P(psi)

.20 (S

) 0 .8 5.0

.357 .047 .481 2.0

.504 .130 .280 1.0

.648 .203 .120 0

.756 .269 .025 -1.0

.800 .300 0 -2.0

TABLE 10.10

Thickness averaged saturations, relative permeabilities and pseudo capillary

pressures corresponding to figs. 10.28 and 10.29

The

k(S)and

k(S)relationships are the thickness averaged relative permeabilities

and will be referred to as such in the remainder of this chapter. In the literature they are

frequently called pseudo relative permeabilities, or simply "pseudo-curves". This author

feels, however, that there are already a sufficient number of "pseudos" in reservoir

engineering without introducing another to describe parameters derived from a simple

averaging process.

As might be expected the averaged relative permeability curves are intermediate

between the rock curves (H >> h) and the linear relations for segregated flow (H << h).

Using the averaged curves in effect reduces the description of the displacement

process from two to one dimension, along the centre line of the reservoir. The curves

can therefore be used in conjunction with the one dimensional Buckley Leverett theory

by drawing the corresponding fractional flow curve and applying the practical graphical

technique of Welge, described in sec. 10.5 and illustrated in exercise 10.2, to

determine oil recovery as a function of cumulative water injected and time. The results

obtained from such calculations, for the same linear reservoir model described in

exercises 10.2 and 10.3 and at the same injection rate of 1000 rb/d

(

= 5 cp;

= .5 cp), are shown in fig. 10.32 and again are intermediate between

those obtained assuming the diffuse flow condition (table 10.5; fig. 10.17) and

segregated flow (table 10.6; fig. 10.24).

The graphical technique for determining averaged relative permeabilities is rather

laborious and has only been included in this section for illustrative purposes. In practice

it is very easy to compute the functions using a simple computer program for which the

necessary input data include rock relative permeabilities and the capillary pressure

function. Average saturations and permeabilities can then be obtained by numerically

evaluating the integrals equs. (10.63-65) for different elevations of the maximum

saturation S

= 1−S

Also listed in table 10.10 are values of

the pseudo capillary pressure (a real

"pseudo"!). This is simply the phase pressure difference between the oil and water at

the centre of the reservoir and the relationship between pseudo capillary pressure and

thickness averaged water saturation, fig. 10.31, is called the pseudo capillary pressure

curve.

IMMISCIBLE DISPLACEMENT 387

DIFFUSE FLOW (ROCK CURVES)

SEGREGATED FLOW

INTERMEDIATE (FINITE CAPILLARY

TRANSITION ZONE)

1.0

0 .1 .2.3.4 .5.6 .7.8.91.0

Fig. 10.30 Averaged relative permeability curves for a homogeneous reservoir, for

diffuse and segregated flow; together with the intermediate case when the

capillary transition zone is comparable to the reservoir thickness

PSEUDO CAPILLARY

PRESSURE

LABORATORY

MEASURED CURVE

-1

-2

.6 1.0.8

P°

(psi)

05101

20 2

time

)

q; = 1000 rb / d

DIFFUSE FLOW (EX. 10.2)

SEGREGATED FLOW (EX. 10.3)

INTERMEDIATE (H h)

(PV)

W (PV)

Fig. 10.31 Capillary and pseudo capillary

pressure curves.

Fig. 10.32 Comparison of oil recoveries for

different assumed water saturation

distributions during displacement.

Let p

and p

be the oil and water pressures at any point in a horizontal reservoir at an

elevation z above the base. If

and

are the corresponding pressures referred to

the centre line of the reservoir then, if the reservoir has a total thickness h, the relations

between p

and

, and p

and,

, under conditions of hydrostatic equilibrium, are

pp z (Darcyunits)

21.013310

æö

=−−

ç÷

èø

and

IMMISCIBLE DISPLACEMENT 388

pp z ("")

21.013310

æö

=−−

ç÷

èø

Subtraction of these equations gives

owcc

pp PP z (atm)

21.0133 10

°° °

∆

æö

−==+ −

ç÷

èø

(10.66)

or, converting to field units

owcc

p p P P 0.4335 z (psi)

°° °

æö

−==+ ∆ −

ç÷

èø

(10.67)

It is convenient to choose the value of z to coincide with the position of the maximum

water saturation, S

= 1−S

, in the reservoir (i.e.

−

). At this point p

−p

= P

= 0

and equations (10.66) and (10.67) can be reduced to

c1S

21.0133 10

−

∆

æö

=−

ç÷

èø

(10.68)

and

c1S

P0.4335 z

−

æö

=∆−

ç÷

èø

(10.69)

respectively. Thus, in the reservoir being currently described (∆

= 0.230; h = 40 ft.)

equ. (10.69) becomes

()

c1S

P0.120z

−

=− (10.70)

From equ. (10.70) it can be seen that the pseudo capillary pressure will vary between

2.0 psi and -2.0 psi as z, the position of the saturation S

= 1 − S

varies between

0 and 40 feet, as shown in fig. 10.33.

Pressure Pressure Pressure

Z = 0

1 -S

P = 2 psi

P = -2 psi

P = 0

water

oil water

oil

wateroil

Z = 20ft

1 -S

Z = 40f

Z = 20ft

Z = 0

Z = 40ft

1 -S

Fig. 10.33 Variation in the pseudo capillary pressure between +2 and -2 psi as the

maximum water saturation S

= 1−

−−

−S

rises from the base to the top of the

reservoir

IMMISCIBLE DISPLACEMENT 389

Values of

as a function ofS

are listed in table 10.10, and the relationship plotted in

fig. 10.31. In particular, the maximum value of

is included for S

= S

= .2, the

connate water saturation. In this case, the water saturation is also 0.2 at the base of

reservoir which, as shown in fig. 27(a), corresponds to a capillary pressure of at least

3 psi. Therefore the phase pressure difference at the centre of the reservoir must be, at

least,

= 5 psi.

Using the combination of averaged relative permeabilities and pseudo capillary

pressure a one dimensional fractional flow equation, representing the average flow

along the centre line of the reservoir, can be developed which is analogous to

equ. (10.9). The only difference will be that the rock relative permeabilities will be

replaced by averaged permeabilities and the capillary pressure gradient term

∂

. And, just as the capillary pressure gradient was neglected in the oil

recovery calculations described in sec. 10.5, so too, the

∂

term is neglected when

drawing the fractional flow curve for the present recovery calculations. The pseudo

capillary pressure-saturation relationship, however, plays an important role in

numerical reservoir simulation which will be described in sec. 10.10.

The methods presented in this section can also be applied in a dipping reservoir. The

averaging is again carried out in the dip normal direction with the result that the

capillary pressures, evaluated in this section as

∝ dz

are replaced throughout by expressions of the form

∝ cos

where z is measured vertically upwards and y in the dip-normal direction from the base

of the reservoir.

10.8 DISPLACEMENT IN STRATIFIED RESERVOIRS

So far, displacement has only been considered in homogeneous, linear reservoirs. In

stratified reservoirs in which there is a defined variation in reservoir parameters with

thickness, in the dip-normal direction, the description of displacement is necessarily

more complex. Nevertheless, the same basic method is used, as described in the

previous section, namely, to generate thickness averaged relative permeabilities as

functions of the thickness averaged water saturation. This will again reduce the

mathematical description to one dimension permitting the use of the Buckley Leverett

theory and the Welge graphical technique (sec. 10.5) for approximate calculations of

the oil recovery.

Two cases can be distinguished, which will both be dealt with in this section. Firstly,

when there is pressure communication between the individual sand layers and vertical

equilibrium pertains across the entire formation thickness and, secondly, when the

IMMISCIBLE DISPLACEMENT 390

individual sands are isolated from one another by impermeable shale layers so that

there is a total lack of pressure communication.

a) With pressure communication between the layers

Consider the case of a 40 ft. thick horizontal reservoir which can be subdivided into

three homogeneous layers each with different thickness, porosity and permeability, as

shown in fig.10.34.

layer 3

layer 2

layer 1

k = 200mD;

k = 100mD;

k = 50mD;

= 0.20;

= 0.17;

= 0.15;

h = 10 ft.

= 20 ft.

= 10 ft.

h = 40 ft

Fig. 10.34 Example of a stratified, linear reservoir for which pressure communication

between the layers is assumed

If the water and oil again have specific gravities of 1.04 and 0.81, respectively then the

capillary pressure is related to capillary rise by the equation

= 0.1 dz (psi) (10.62)

Similarly, the pseudo capillary pressure equation for calculating the phase pressure

difference at the centre of the reservoir is still

c1S

P0.1(20z )

−

=− (10.70)

where

−

is the elevation of the maximum water saturation, S

= 1 − S

, in the

reservoir, at which point the phase pressure P

is always zero. Laboratory measured

relative permeabilities and capillary pressures for the three layers are shown in

fig. 10.35.