Dake L.P. Fundamentals of reservoir engineering

Подождите немного. Документ загружается.

NATURAL WATER INFLUX 321

which on substituting in the inflow equation (9.18) gives

iei

Jp t / W

J(p p)e

−

=−

(9.23)

Finally, integrating equ. (9.23) for the stated initial conditions yields the following

expression for the cumulative water influx

iei

Jp t / W

W(pp)(1e )

−

=−−

(9.24)

What can be observed immediately from this expression is that as t tends to infinity,

then

W(pp)

cW (p p)

−

=−

which is the maximum amount of water influx that could occur once the pressure drop

- p has been transmitted throughout the aquifer.

As it stands, equ. (9.24) is not particularly useful since it was derived for a constant

inner boundary pressure. To use this solution in the practical case, in which the

boundary pressure is varying continuously as a function of time, it should again be

necessary to apply the superposition theorem. Fetkovitch has shown, however, that a

difference form of equ. (9.24) can be used which eliminates the need for superposition.

That is, for the influx during the first time step ∆t

, equ. (9.24) can be expressed as

()

i1 ei

Jp t / W

Wpp(1e )

−∆

∆= − −

(9.25)

where

p is the average reservoir boundary pressure during the first time interval. For

the second interval ∆t

()

i2 ei

Jp t / W

Wpp(1e )

−∆

∆= − −

(9.26)

where

p is the average aquifer pressure at the end of the first time interval and is

evaluated using equ. (9.20) as

pp1

æö

∆

=−

ç÷

èø

(9.27)

In general for the n

time period,

()

n1n

in ei

Jp t / W

Wpp(1e )

−

−∆

∆= − −

(9.28)

where

NATURAL WATER INFLUX 322

pp1

−

æö

∆

ç÷

=−

ç÷

èø

(9.29)

The values of

p , the average reservoir boundary pressure, are calculated, as

described in section 9.3, as

n1 n

−

(9.15)

Fetkovitch has demonstrated that using equs. (9.28) and (9.29), in a stepwise fashion,

the water influx calculated for a variety of different aquifer geometries matches closely

the results obtained using the unsteady state influx theory of Hurst and van Everdingen

for finite aquifers.

Values of the aquifer productivity index J, which depend both on the geometry and

flowing conditions, are listed in table 9.8, in Darcy units. Multiplying the radial Pl

functions by 7.08×10

-3

and the linear by 1.127×10

-3

will convert these expressions to

field units. The radial values of J for semi-steady state and steady state influx will be

recognised as identical in form to the productivity indices listed in Chapter 6, table 6.1,

for the flow of a liquid into a wellbore. The only difference is that r

, the reservoir radius,

now replaces r

, the wellbore radius. Note also that, while semi-steady state

expressions for J, equs. (9.30), are used in conjunction with the Fetkovitch

equations (9.28) and (9.29), the steady state expressions, (9.31), are used in a

different manner. In applying these values it is assumed that the water influx from the

aquifer into the reservoir is replaced by water from an external source, such as an

artesian water supply, so that the pressure

Flowing Condition Radial Aquifers

J (cc/sec/atm)

Linear Aquifers

J (cc/sec/atm)

Semi-steady state

(used with drawdown

expressed as

pp− )

2fkh

æö

−

ç÷

èø

khw

(9.30)

Semi-steady state

(used with drawdown

expressed as

pp− )

2fkh

khw

(9.31)

TABLE 9.8

at the external boundary of the aquifer remains constant at its initial value p

. In this

case it is unnecessary to keep evaluating the average pressure in the aquifer since it

remains unchanged. The J values expressed in equ. (9.31) are now used in

conjunction with the drawdown measured as p

- p. Referring to equ. (9.23),

NATURAL WATER INFLUX 323

iei

Jp t / W

qJ(pp)e

−

==−

(9.23)

the steady state case implies that W

, the encroachable water, is infinite and therefore

qJ(pp)

==−

(9.32)

which, upon integration, gives the cumulative water influx as

WJ(pp)dt=−

(9.33)

Equs. (9.32) and (9.33), which are a special case of Fetkovitch's theory, were first

presented in 1936 by Schilthuis

and described as steady state influx equations.

Equation (9.33) can be evaluated in stepwise fashion in which values of

p , the inner

boundary pressure during the n

time period, are calculated using equ. (9.15).

The reader should also be aware that the PI expressions presented in table 9.8 were

derived in similar form in Chapter 6, sec. 2, under the assumption that (r

)

was

approximately zero. For small radial aquifers, the equivalent assumption that (r

)

negligible may not always be applicable and the correct PI expression should then be

obtained by solving the radial diffusivity equation, using exactly the same steps as

shown in Chapter 6 but, without neglecting such terms. Considering the inherent

uncertainties in aquifer fitting this approach is generally unnecessary and, in fact,

Fetkovitch has demonstrated an almost perfect match between his results and those of

Hurst and van Everdingen for values of r

as small as three.

For the case of a reservoir asymmetrically situated within a non-circular shaped aquifer

it should, with tolerable accuracy, be possible to use the Dietz shape factors presented

in fig. 6.4, and described in Chapter 7, sec. 7, to modify the semi-steady state PI

expressions. Thus the radial PI in equ. (9.30) can be generalised as

2fkh

2Cr

which has precisely the same form as equ. (6.22).

For very large aquifers, the initial flow of water into the reservoir will be governed by

transient flow conditions. In this case, it takes a finite time for the initial pressure

disturbance at the reservoir-aquifer boundary to feel the effect of the outer boundary of

the aquifer. Unfortunately, during this transient flow period it is no longer possible, in

analogy with wellbore equations, to derive a simple expression for the productivity

index J. This is because for inflow into a reservoir it is incorrect to use the approximate

line source solution of the radial diffusivity equation, in an attempt to evaluate a PI

under transient conditions, since r

is always finite and the boundary conditions for this

type of solution, expressed in equ. (7.1), can no longer be justified. Therefore, the

method of Fetkovitch cannot be used for the description of influx from an infinite aquifer

NATURAL WATER INFLUX 324

and, when dealing with very large, finite aquifers, it is initially still necessary to apply

the unsteady state influx theory of Hurst and van Everdingen for the first few time

steps. The following example will illustrate the speed and accuracy in using the method

of Fetkovitch in comparison to that of Hurst and van Everdingen. In addition, it will

demonstrate how the two methods can be combined when dealing with a large aquifer,

= 10, in which, for the first few years, the influx occurs under transient flow

conditions.

EXERCISE 9.3 WATER INFLUX CALCULATIONS USING THE METHOD OF

FETKOVITCH

Recalculate the cumulative water influx as a function of time, using all the reservoir and

aquifer data presented in exercise 9.2, but applying the method of Fetkovitch. Perform

the calculations for both r

= 5 and 10.

EXERCISE 9.3 SOLUTION

Using the method of Fetkovitch the following two equations are required

pp1

−

æö

∆

ç÷

=−

ç÷

èø

(9.29)

and

n1n

in ei

Jp t / W

W(pp)(1e )

−

−∆

∆= − −

(9.28)

where

n-1

p is the average pressure in the aquifer at the end of the (n - 1)

time

interval

and

p is the average reservoir-aquifer boundary pressure during the n

time

interval.

Since in this present application a history match is being sought for available reservoir

pressures, that is, values of

p which are listed in column 3 of table 9.2 in the previous

exercise, the manner of solving the above equations, to explicitly calculate the

cumulative water influx, is as follows

- having obtained ∆W

n-1

1for the n - 1

time step

then W

n-1

−

∆

- using equ. (9.29), evaluate

−

- insert

−

in equ. (9.28) and solve for ∆W

NATURAL WATER INFLUX 325

For the first time step

n-1

p = p

, the initial reservoir and aquifer pressure.

The constant terms in equs. (9.28) and (9.29) can be evaluated (in field units), for the

correct aquifer size, i.e. r

= 5, as follows:

()

ei i i

eo i

WcWp

cf r r h p / 5.615 rb

7 10 .3889 (2116 85) 10 100 .25 2740

5.615

W 211.9 MMrb

πφ

−

=−

× × × −××××

For a finite radial aquifer

7.08 10 fkh

7.08 10 .3889 200 100

116.5b / d / psi

.55(In5 .75)

−

æö

−

ç÷

èø

×× ××

−

(9.30)

Therefore, Jp

= 116.5×2740/211.9×10

= 1.506×10

-3

/day

Since the ∆t in equ. (9.28) is in days, then for time steps of one year

iei

Jp t / W

1.506 10 365 0.4229

1e 1e

−

−∆

−××=

−=−

Equ. (9.28) can therefore be reduced to

()

nn1

ean

211.9 10

Wpp0.4229

2740

W 32705 p p rb

−

∆= −×

∆= −

NATURAL WATER INFLUX 326

The calculation of the water influx is as shown in table 9.9.

Time

(years)

(psia)

−

(psi)

W∆

(MMrb)

(psia)

0 2740(p

)

1 2620 120 3.925 3.925 2689

2 2395 294 9.615 13.540 2565

3 2199 366 11.970 25.510 2410

4 2029 381 12.461 37.971 2249

5 1883 366 11.970 49.941 2094

6 1760 334 10.924 60.865 1953

7 1655 298 9.746 70.611 1827

8 1571 256 8.373 78.984 1719

9 1507 212 6.934 85.918 1629

10 1460 169 5.527 91.445 1558

TABLE 9.9

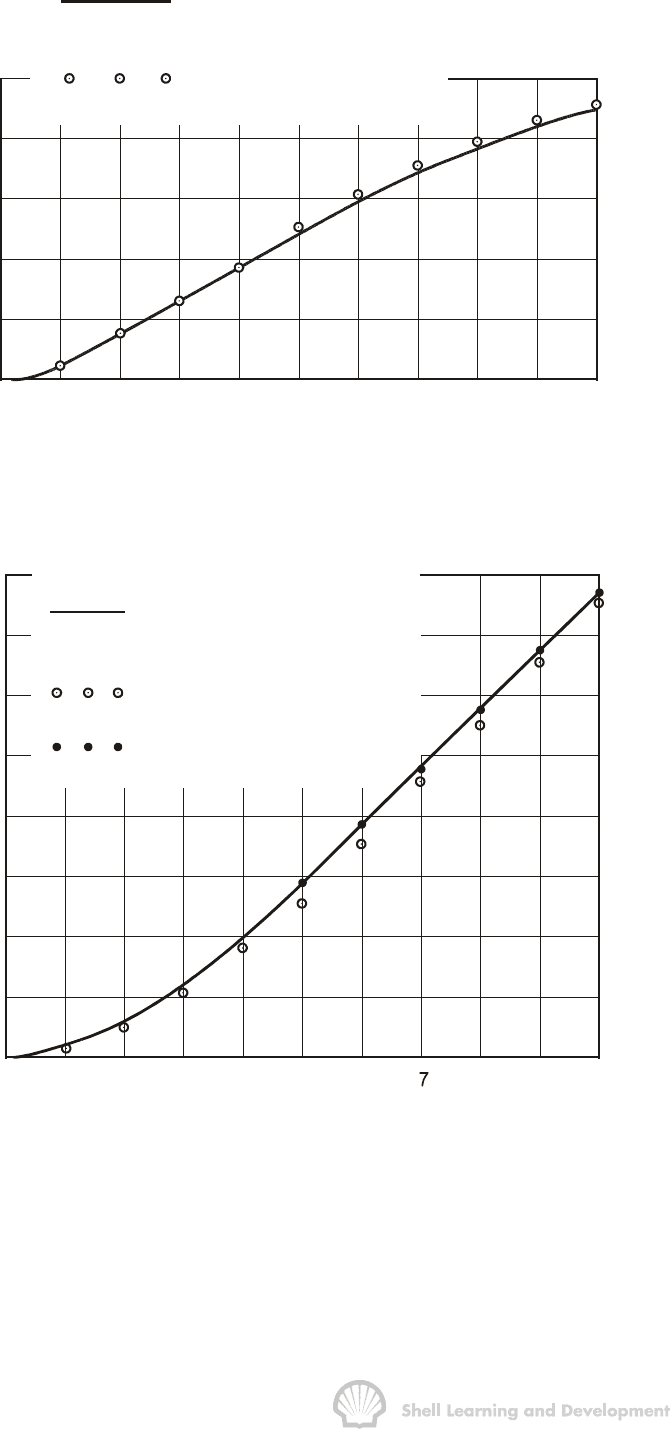
The cumulative water influx is shown in fig. 9.16, in comparison to that calculated in

exercise 9.2, for r

= 5, (table 9.7). As can be seen, the agreement between the two is

excellent.

The water influx has been recalculated, using the method of Fetkovitch, for r

= 10, in

which case: W

= 874.2 MMrb; J = 64.5 b/ d/psi and the influx equation becomes

∆W

= 22685

−

− This influx, as a function of time, is shown in fig. 9.17, in which

it can be seen that there is a disparity between this and the unsteady state influx

calculated in table 9.5. This is because the method of Fetkovitch cannot correctly

model the early, transient influx from a large aquifer. The figures can be improved by

applying the Hurst and van Everdingen method for the first few years, which is

computationally simple, and then switching to Fetkovitch's method. This procedure is

illustrated in table 9.10, using values of W

from table 9.5, for the first four years.

NATURAL WATER INFLUX 327

(MMrb)

100

Hurst, van Everdingen

(table 9.7)

891

Fetkovitch

(table 9.9)

Time (years)

Fig. 9.16 Comparison between Hurst and van Everdingen and Fetkovitch for r

= 5

160

120

100

140

(MMrb)

r= 10

Hurst, van Everdingen

(table 9.5)

Fetkovitch

Fetkovitch (modified)

(table 9.10)

Time

ears

)

Fig. 9.17 Comparison between Hurst and van Everdingen and Fetkovitch for r

= 10

NATURAL WATER INFLUX 328

Time

(years)

(psia)

n-1

p-p

(psi)

∆W

(MMrb)

(psia)

0 2740 2740

1 2620 3.829 2728

2 2395 13.460 2698

3 2199 26.462 2657

4 2029 41.935 2609

5 1883 726 16.469 58.404 2557

6 1760 797 18.080 76.484 2500

7 1655 845 19.169 95.653 2440

8 1571 869 19.713 115.366 2378

9 1507 871 19.759 135.125 2316

10 1460 856 19.418 154.543 2256

TABLE 9.10

Using this combined method (Fetkovitch-modified) it can be seen that the results are

almost identical with those obtained using the unsteady state influx theory throughout,

as shown in fig. 9.17.

9.5 PREDICTING THE AMOUNT OF WATER INFLUX

Sections 9.2 through 9.4 considered the ways in which a mathematical aquifer model is

constructed and matched to the reservoir production and pressure history. If it is felt

confident that the model so developed is satisfactory in matching the history, then the

next step is to use it in predicting the future reservoir performance. The aim here is

usually to determine how the reservoir pressure will decline for a given offtake rate of

reservoir fluids. A knowledge of this decline will assist in calculating the recovery factor,

consistent with production engineering and economic constraints. All the mathematical

tools necessary to perform such an exercise have already been presented; all that is

necessary to consider is how to solve the various equations to explicitly determine the

pressure.

The basic equations are the reservoir material balance and the water influx equation.

These can be solved simultaneously, by an iterative process, to give the reservoir

pressure. To illustrate the method of solution the case of water influx into a gas

reservoir will be considered for which the material balance is very simple and, as

shown in Chapter 1, sec. 7, can be expressed as

eii

WEp

ZZ G G

æö

=− −

ç÷

èø

(1.41)

NATURAL WATER INFLUX 329

in which the cumulative gas production G

is constrained to meet a fixed market offtake

rate. The methods of Hurst and van Everdingen and Fetkovitch will be described

separately.

a) Hurst and van Everdingen

pressure

n-2

n-1

n-2 n-1 n

time

Fig. 9.18 Predicting the pressure decline in a water drive gas reservoir

Fig. 9.18 illustrates the situation. Up to time level n - 1 everything has been determined

and the water influx up to this point has been correctly included in the material balance.

The next step is the determination of p

, the current reservoir pressure at the end of the

time interval, that is at time T. The water influx is then

()

ejDDD

WUpWTt

−

=∆ −

(9.17)

which may be expanded as

()

njn1

ejDDDn1DDD

WUpWTt UpWTt

−

=∆ −+∆ −

(9.34)

and, using equ. (9.16)

n2 n

−

∆=

equ. (9.34) may be written as

()

nj n1

e jDD D n2 n DD D

WUpWTt p pWTt

−

=∆ −+ − −

(9.35)

In this equation there are only two unknowns

W and

p . These two are also related

through the material balance

pei

GWE

ZZ G G

æöæ ö

æö

=− −

ç÷ç ÷

ç÷

èø

èøè ø

(9.36)

A convenient way of solving equs. (9.35) and (9.36) is by the iterative method shown in

fig. 9.19. The sequence of steps during any time period may be described as follows.

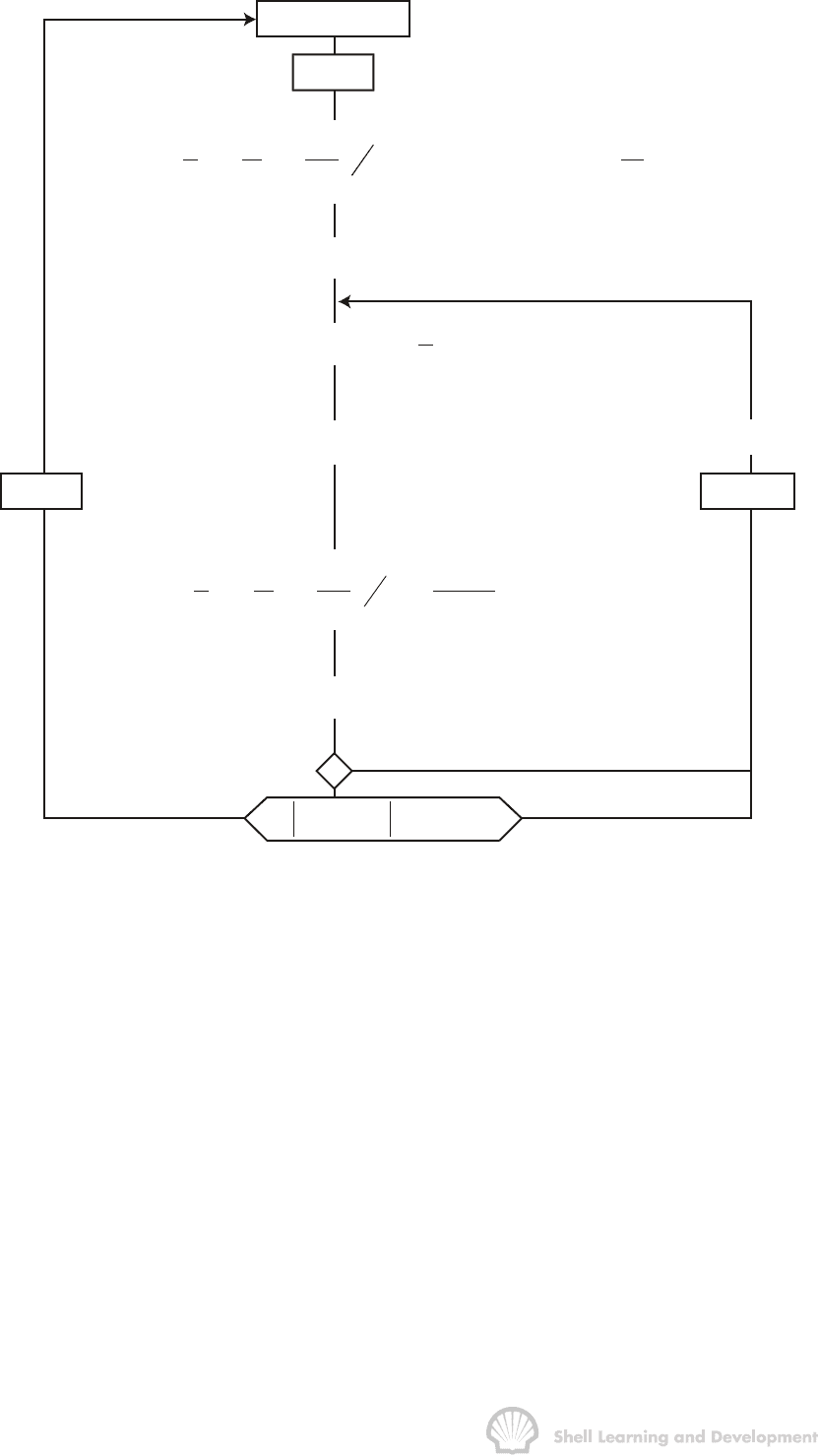
NATURAL WATER INFLUX 330

k = 1

Time step = n

jD D D

11UpW(Tt)

ZZ G G

−

=α

ç÷

=− − ∆ −

ç÷

nj n1

e jDD D n2 n DD D

WU pW(Tt) (p p)W(Tt)

−

=∆ −+ − −

-1

n=n+1

pei

GWE

ZZ G G

æö

ç÷

=− −

ç÷

èø

k =

pp TOL

−

−−

= iteration counter

TOL = tolerance pressure

difference

(

psi

)

Fig. 9.19 Prediction of gas reservoir pressures resulting from fluid withdrawal and

water influx (Hurst and van Everdingen)

Make an initial estimate of the reservoir pressure p

= p

at the end of time step n by

evaluating the material balance equation with the water influx initially set equal to

()

ejDDD

WUpWTt

−

=∆ −

(9.37)

i.e. neglecting the final term U∆p

n-1

– t

n-1

) in equ. (9-35).

Note: one could also use the value of

−

, the water influx after time step n-1, in the

material balance but equ. (9.37) is usually closer to the actual influx and will lead to a

smaller number of iterations.