Dake L.P. Fundamentals of reservoir engineering
Подождите немного. Документ загружается.


NATURAL WATER INFLUX 301
Darcy Units Field Units
D
2
kt
t
cL
φµ
=
(t-sec) t
D
= constant ×
2
kt
cL
φµ
(9.9)
constant, same as for equ. (9.7)
U = wLh
φ
c (cc/atm) U = .1781 wLh
φ
c (bbl/psi) (9.10)
Other characteristic features of the plots of W
D
(t
D
) versus t
D
depend upon whether the
aquifer is bounded or infinite in extent.
Bounded Aquifers
Irrespective of the geometry there is a value of t
D
for which the dimensionless water
influx reaches a constant maximum value. This value is, however, dependent upon the
geometry as follows
()
()
2
1
2
DeD
Radial W max r 1=− (9.11)
()
D
Linear W max 1= (9.12)
Note that if W
D
in equ. (9.11) is used in equ. (9.4), for a full radial aquifer (f = 1), the
result is
22
2
e0
1
2
e0
2
0
22
e0
(r r )
W2hcrp
r
(r r )h c p
πφ
πφ
−
=×∆×
=− ∆
But this latter expression is also equivalent to the total influx occurring, assuming that
the ∆p is instantaneously transmitted throughout the aquifer. A similar result can be
obtained using equ. (9.12) for linear geometry. Therefore, once the plateau level of
W
D
(t
D
) has been reached, it means that the minimum value of t
D
at which this occurs
has been sufficiently large for the instantaneous pressure drop ∆p to be felt throughout
the aquifer. The plateau level of W
D
(t
D
) is then the maximum dimensionless water influx
resulting from such a pressure drop.
Infinite Aquifer
Naturally, no maximum value of W
D
(t
D
) is reached in this case since the water influx is
always governed by transient flow conditions. For radial geometry, values of W
D
(t
D
)
can be obtained from the graphs for r
eD
= ∞. There is no plot of W
D
(t
D
) for an infinite
linear aquifer. Instead, the cumulative water influx can be calculated directly using the
following equation
e
kct
W2hw p(ccs)
φ
πµ
=×∆ (9.13)
NATURAL WATER INFLUX 302
which is expressed in Darcy units. The corresponding equation in field units, with t
measured in hours, is
3
e
kct
W3.2610hw xp (bbls)
φ
πµ
−
=× ∆ (9.14)
Note that dimensionless time is not used in the above equations.
r= 1.5
eD
r= 2.0
eD
r= 2.5
eD
r
=
3
.
0
e
D
r
=
3
.
5
e
D
r
=
4
.
0
e
D
r
=
e
D
7.06.05.04.03.02.01.00
0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.
0
W
D
t
D
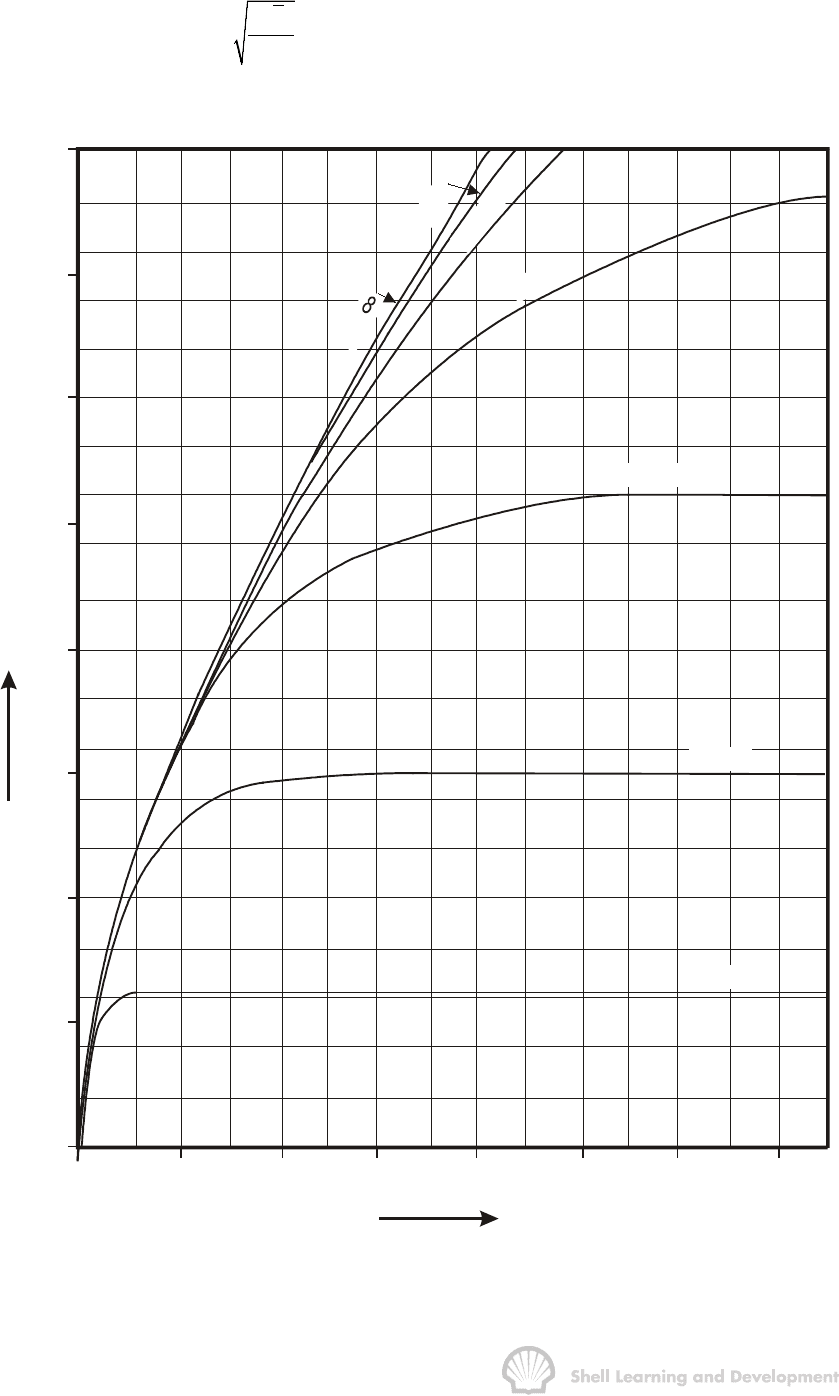
Fig. 9.3 Dimensioniess water influx, constant terminal pressure case, radial flow.
(After Hurst and van Everdingen, ref. 1)
NATURAL WATER INFLUX 303
0
0
2
4
6
8
10
12
14
16
18
20
10 20 30 40 50 60 70
r= 3.0
eD
r= 3.5
eD
r =5.0
D
e
r
=
6
.
0
=
7
.
0
r
=
8
.
0
r = 4.5
D e
r=4.0
eD
r
=
8
e
D
e
D
e
D
r
e
D
W
D
t
D
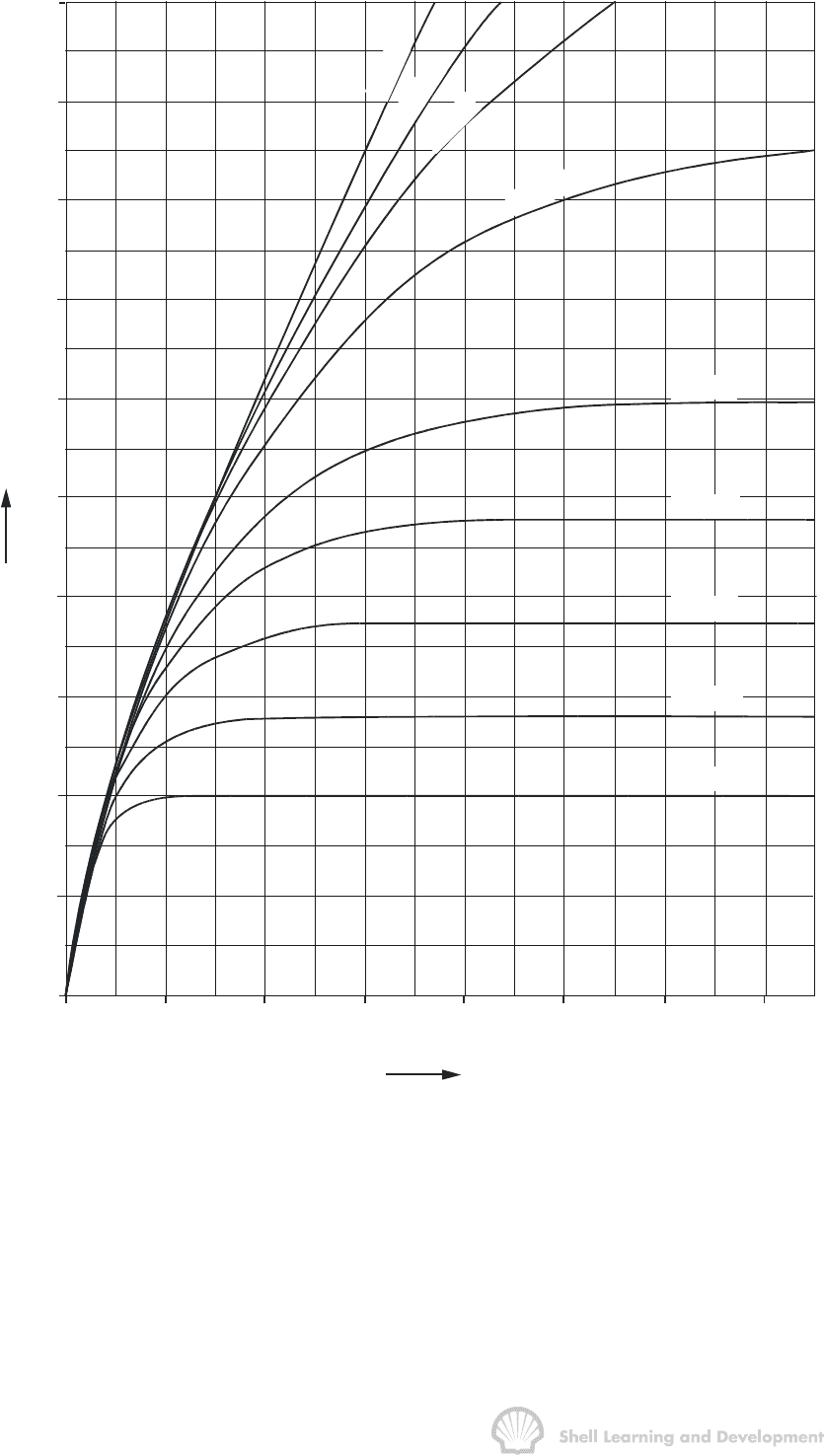
Fig. 9.4 Dimensionless water influx, constant terminal pressure case, radial flow
(After Hurst and van Everdingen, ref. 1)
NATURAL WATER INFLUX 304
110
100
90
70
80
60
50
40
30
20
10
0
0 20 40 60 80 100 120 140 160 180 200
r=5.0
eD
r=6.0
eD
r
=
7
.
0
e
D
r
=8
.0
e
D
r
=
9
.
0
e
D
r
=
1
0
.
0
e
D
r
=
e
D
8
W
D
t
D
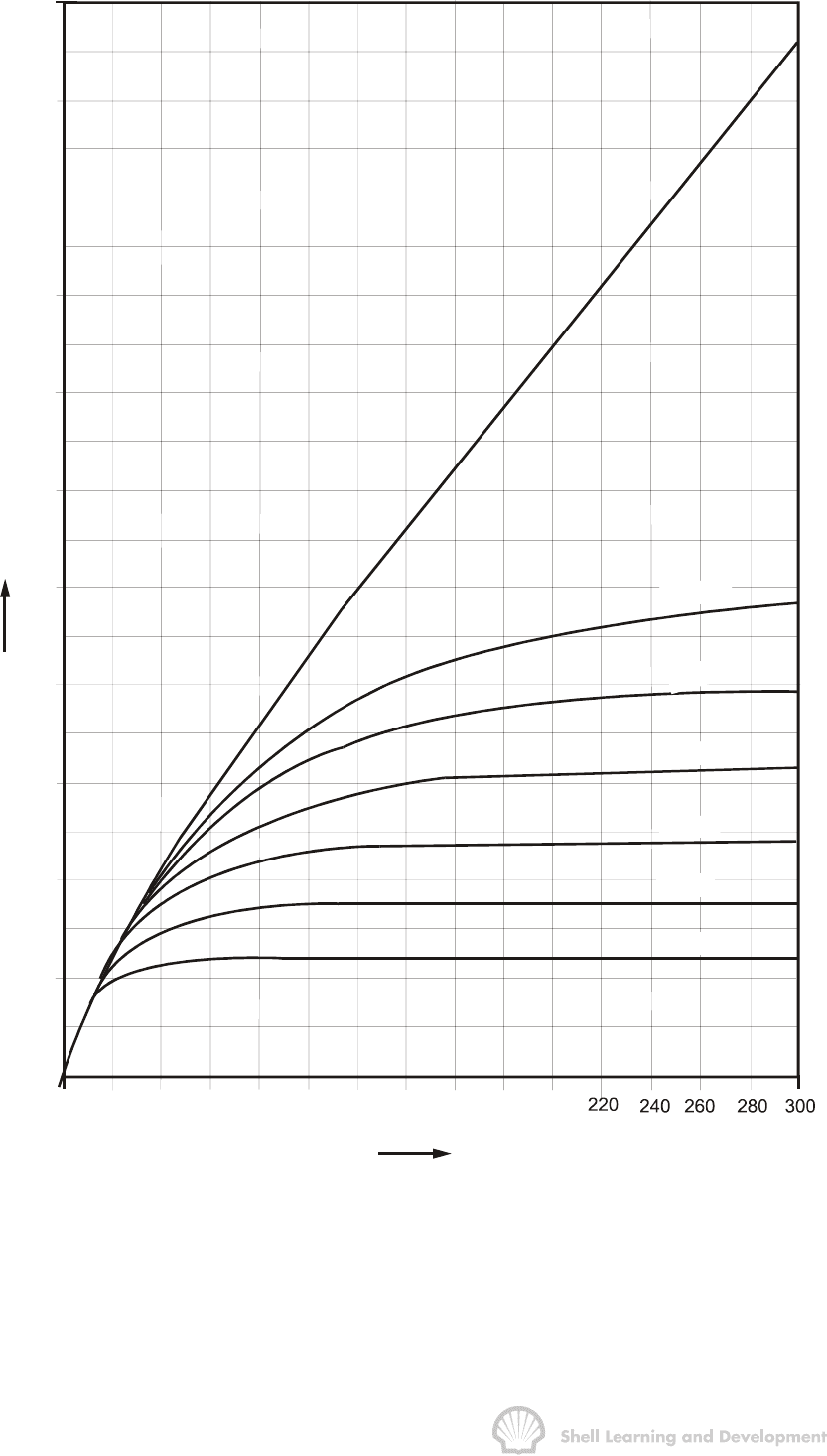
Fig. 9.5 Dimensionless water influx, constant terminal pressure case, radial flow
(After Hurst and van Everdingen, ref. 1)
NATURAL WATER INFLUX 305
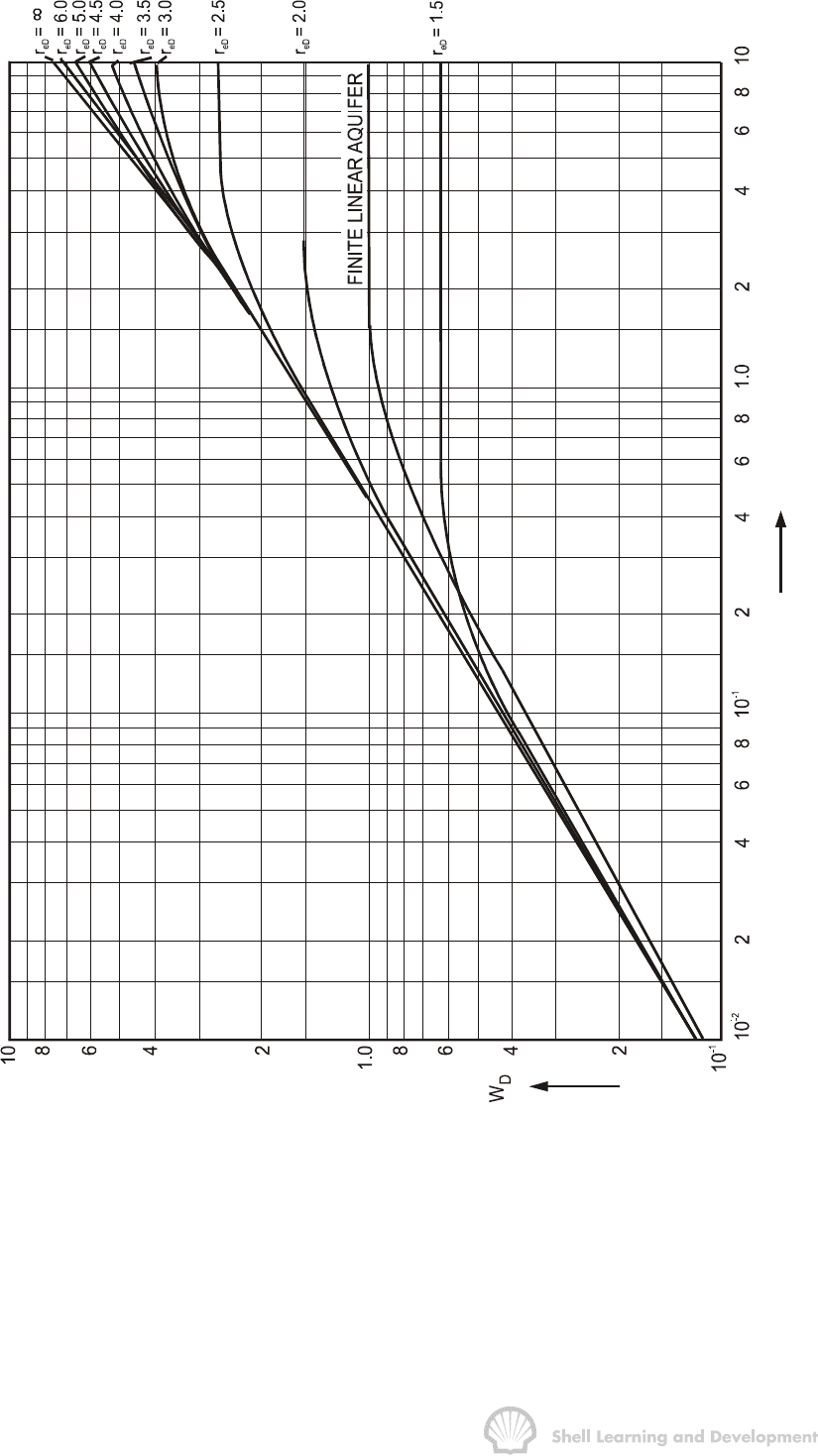
t
D
Fig. 9.6 Dimensionless water influx, constant terminal pressure case, radial and
linear flow (After Hurst and van Everdingen, ref.1)

NATURAL WATER INFLUX 306
USE THIS SCALE FOR LINE reD = (CON’T) ONLY
8
10
2
8
6
4
2
10
8
6
4
2
1
10 2468
10
2
4682
10
3
2468
10
4
10
10
2
10
3
r =15.0
eD
r
=
e
D
(
c
o
n
t
’
d
)
8
r
=
e
D
8
r=2.5
eD
r=3.0
eD
r=3.5
eD
r=4.0
eD
r=4.5
eD
r=5.0
eD
r=7.0
eD
r=7.0
eD
r=8.0
eD
r=9.0
eD
r=10.0
eD
r=6.0
eD
W
D
t
D
Fig. 9.7 Dimensionless water influx, constant terminal pressure case, radial and
linear flow (After Hurst and van Everdingen, ref.1)
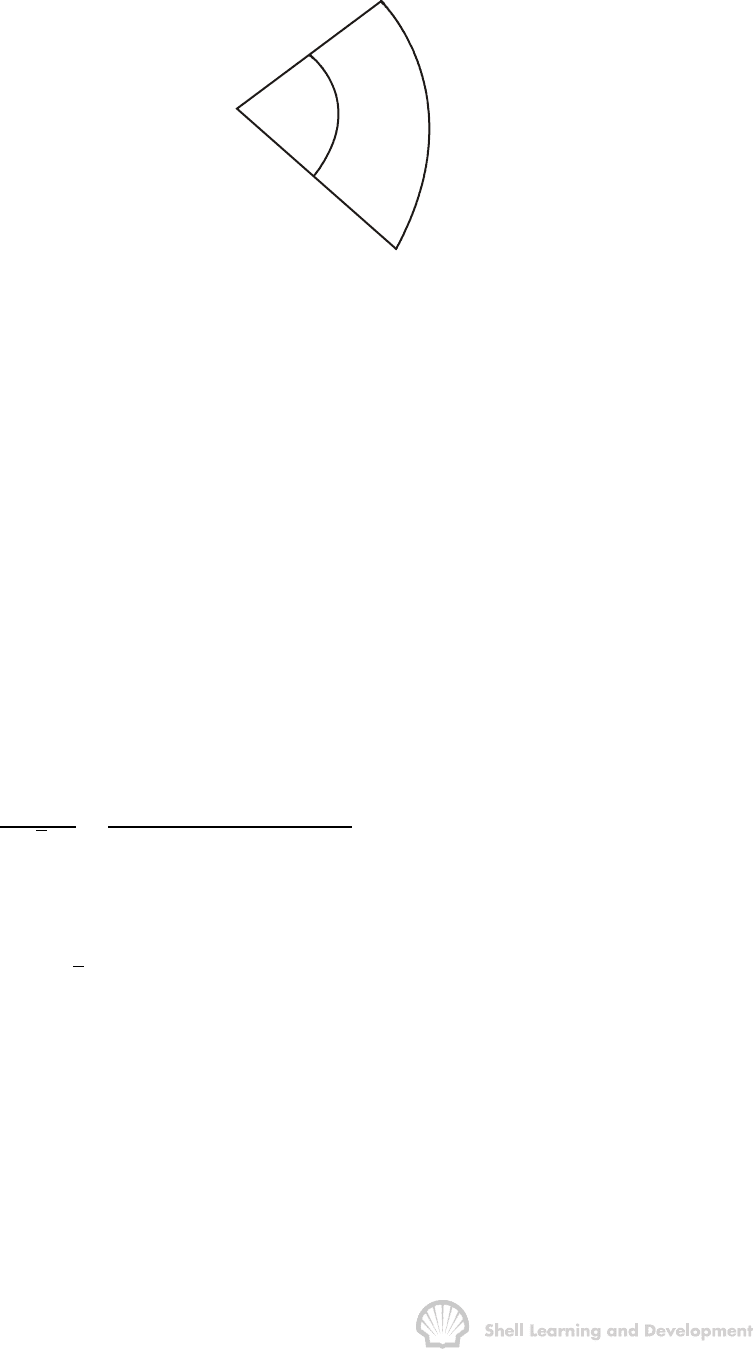
NATURAL WATER INFLUX 307
EXERCISE 9.1 APPLICATION OF THE CONSTANT TERMINAL PRESSURE
SOLUTION
A reservoir-aquifer system has the geometry and dimensions as shown in fig. 9.8.
r = 5000’
o
r = 15000’
e
Oil
80
O
Water
Fig. 9.8 Water influx from a segment of a radial aquifer
If the aquifer properties are as follows
h = 50 ft µ = 0.4 cp
φ
=0.25 c
w
=3.0×10
-6
/psi
k = 50 mD c
f
=6.0×10
-6
/psi
1) Calculate the water influx at times t = 0.5, 1, 1.5, 2 and 3 years after an instantaneous
pressure drop of ∆p = 100 psi, at the oil water contact, at time t=0.
2) What would be the corresponding water influx if it is assumed that the same pressure
drop is transmitted instantaneously throughout the aquifer?
EXERCISE 9.1 SOLUTION
1) Since t is measured in years, then
D
62
2
0
D
2.309kt 2.309 50 t
t
.25 .4x9 10 (5000)
cr
t5.131t
φµ
−
××
==
×××
=
The encroachment angle is 80°, therefore f = 80°/360° = 0.222 and
W
e
= 1.119 f
φ
h
2
0
cr ∆pW
D
(t
D
)
= 1.119×.222×.25×50×9×10
-6
×(5000)
2
×100W
D
(t
D
)
W
e
= 69868 W
D
(t
D
) bbls

NATURAL WATER INFLUX 308
Using figs. 9.3 and 9.4 to obtain values of W
D
(t
D
); W
e
can be calculated as follows:
t
(years)
t
D
W
D
(t
D
)
(r
eD
= 3.00)
W
e
(bbls)
.5 2.6 2.7 188644
1.0 5.1 3.5 244538
1.5 7.7 3.8 265498
2.0 10.3 3.9 272485
3.0 15.4 4.0 279472
TABLE 9.1
For dimensionless times greater than t
D
=15, W
D
(t
D
) = 4 and remains constant at this
value indicating that the maximum amount of water influx due to the 100 psi pressure
drop is 279500 bbl.
2) If the pressure drop is transmitted instantaneously throughout the aquifer, then
W
e
=
()
22
eo
cf r -r
π
h
φ
∆p/5.615 bbls
= 9 × 10
-6
× .222 × π (15000
2
− 5000
2
) × 50 × .25 × 100/5.615
W
e
= 279500 bbls
which again is the maximum water influx due to the 100 psi pressure drop. In using the
constant terminal pressure solution, a time scale has been attached to the water influx.
9.3 APPLICATION OF THE HURST, VAN EVERDINGEN WATER INFLUX THEORY IN
HISTORY MATCHING
In the previous section the cumulative water influx into a reservoir, due to an
instantaneous pressure drop applied at the outer boundary, was expressed as
()
eDD
WUpWt=∆ (9.5)
In the more practical case of history matching the observed reservoir pressure, it is
necessary to extend the theory to calculate the cumulative water influx corresponding
to a continuous pressure decline at the reservoir-aquifer boundary. In order to perform
such calculations it is conventional to divide the continuous decline into a series of
discrete pressure steps. For the pressure drop between each step, ∆p, the
corresponding water influx can be calculated using equ. (9.5). Superposition of the
separate influxes, with respect to time, will give the cumulative water influx.
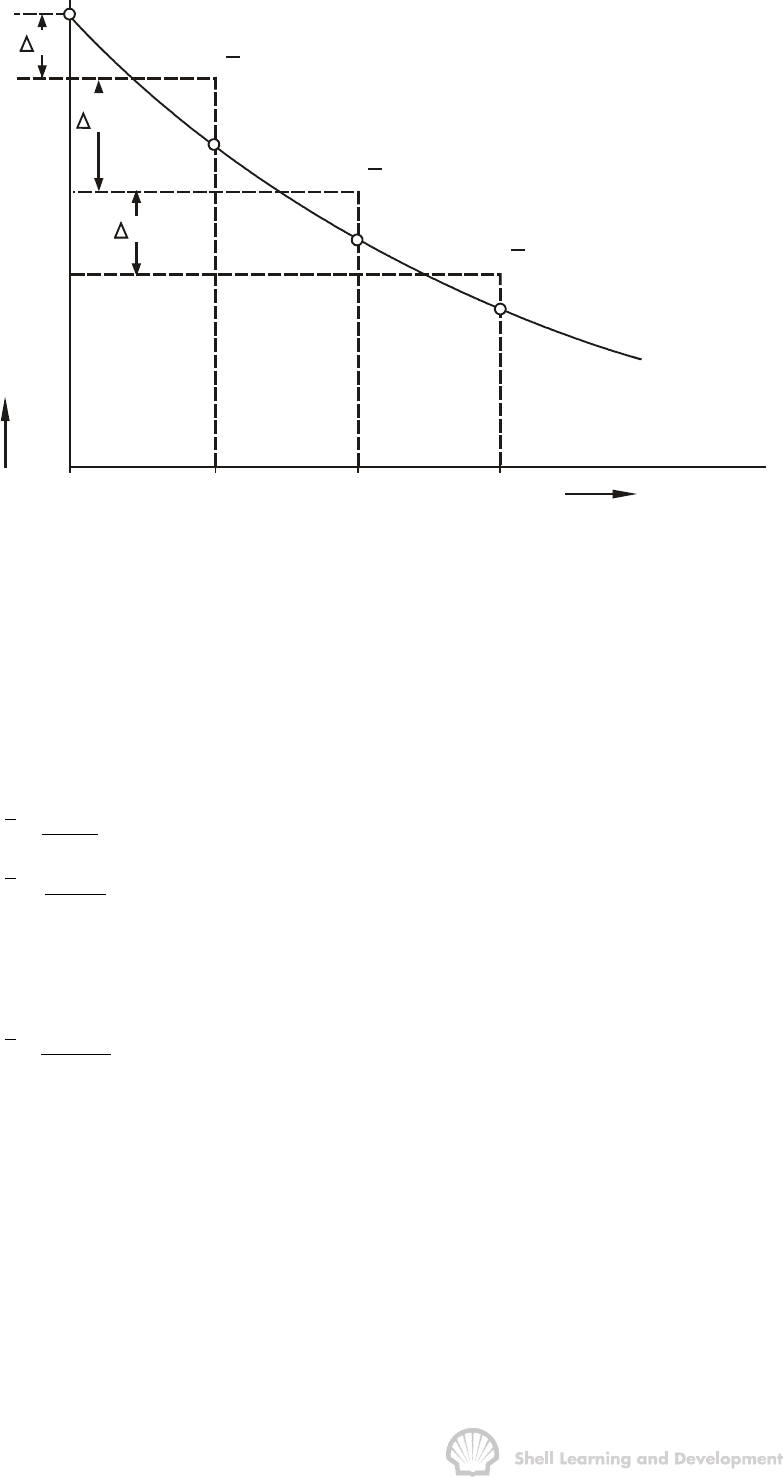
The recommended method of approximating the continuous pressure decline, by a
series of pressure steps, is that suggested by van Everdingen, Timmerman and
McMahon
3
, which is illustrated in fig. 9.9.
NATURAL WATER INFLUX 309
PRESSURE
TIME
p
2
p
1
p
0
p
1
p
1
p
i
p
2
0t
1
t
2
t
3
p
2
p
3
p
3
Fig. 9.9 Matching a continuous pressure decline at the reservoir-aquifer boundary by
a series of discrete pressure steps
Suppose that the observed reservoir pressures, which are assumed to be equal to the
pressures at the original hydrocarbon-water contact, are p
i
, p
1
, p
2
, p
3
.... etc., at times 0,
t
1
, t
2
, t
3
.... etc. Then the average pressure levels during the time intervals should be
drawn in such a way that
i1
1
12
2
j
1j
j
pp
p
2
pp
p
2
pp
p
2
−
+
=
+
=
+
=
C
C
C
(9.15)
The pressure drops occurring at times 0, t
1
, t
2
. . . etc. are then
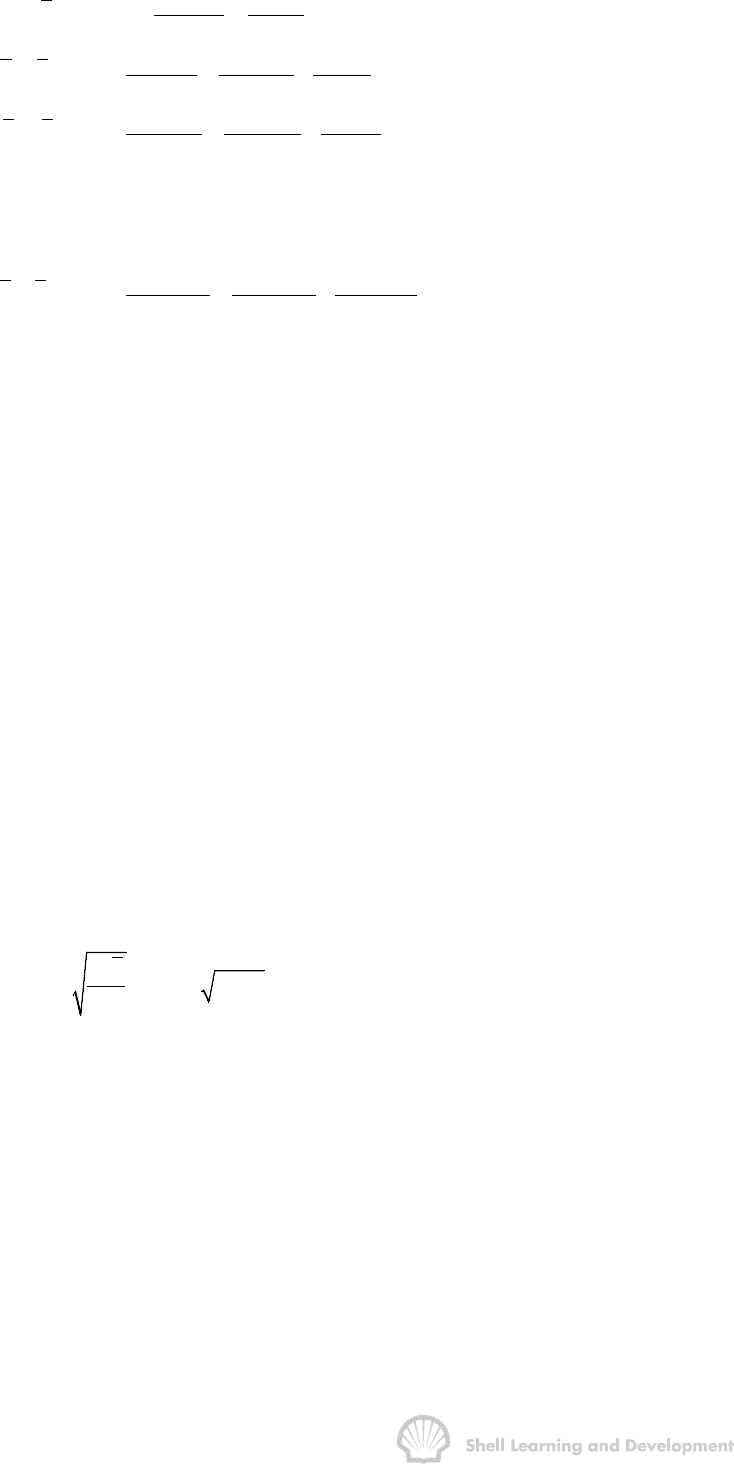
NATURAL WATER INFLUX 310
i1 i1
10i i
i1 12 i2
121
23 1312
232
j
1j j j1 j1j1
jj1j
(p p ) p p
ppp p
22
(p p ) (p p ) p p
ppp
222
(p p ) p p
(p p )
ppp
222
(p p ) (p p ) p p
ppp
222
−
−+−+
+
+−
∆=− = =
++−
∆=− = − =
+−
+
∆=− = − =
++ −
∆=− = − =
C
C
C
(9.16)
Therefore, to calculate the cumulative water influx W
e
at some arbitrary time T, which
corresponds to the end of the n
th
time step, requires the superposition of solutions of
type, equ. (9.5), to give
W
e
(T) = U [∆p
o
W
D
(T
D
)+∆p
1
W
D
(T
D
- t
D1
)+ ∆p
2
W
D
(T
D
- t
D
2
)
+………….∆p
j
W
D
(T
D
- t
D
j
)+…∆p
n-1
W
D
(T
D
- t
D
n-1
)]
where ∆p
j
is the pressure drop at time t
j
, given by equ. (9.16), and W
D
(T
D
- t
D
j
) is the
dimensionless cumulative water influx, obtained from figs. 9.3 - 9.7, for the
dimensionless time T
D
- t
D
j
during which the effect of the pressure drop is felt. Summing
the terms in the latter equation gives
()
j
n1
ejDDD
j0
WT U pW(T T)
−
=
=∆ −
å
(9.17)
In the special case of an infinite, linear aquifer for which, as noted in sec. 9.2, there is
no W
D
function included in figs. 9.3 - 9.7, the cumulative water influx at time T due to a
step-like pressure decline at the aquifer-reservoir boundary can be calculated using
equ. (9.13) as
()
n1
ejj
j0
kc
WT 2hw p T t
φ
πµ
−
=
=∆−
å
which, when expressed in field units has the same constant, 3.26×10
-3
, as equ. (9.14).
The following exercise will illustrate the application of the method of superposition in
history matching.
EXERCISE 9.2 AQUIFER FITTING USING THE UNSTEADY STATE THEORY OF
HURST AND VAN EVERDINGEN
A wedge shaped reservoir is suspected of having a fairly strong natural water drive.
The geometry of the reservoir-aquifer system is shown in fig. 9.10.
