Dake L.P. Fundamentals of reservoir engineering

Подождите немного. Документ загружается.

IMMISCIBLE DISPLACEMENT 341

owc

pp P gH

−==∆ (10.2)

where ∆

. Furthermore, considering in detail the geometry at the interface in

the capillary tube, fig. 10.4. If the curvature is approximately spherical with radius R,

then in applying the Laplace equation, (10.1), r

= r

= R at all points on the interface.

Also if r is the radius of the capillary tube, then r = RcosΘ and therefore

owc

2cos

pp P gh

−== =∆

(10.3)

This equation is frequently used to draw a comparison between simple capillary rise

experiments, as described above, and capillary rise in the reservoir, the porous tracts

in the latter being likened to a collection of capillary tubes with different radii. In this

comparison it can be seen that the capillary rise of water will be greater for small r,

equ. (10.3), and will decrease as r increases. The decrease in capillary rise will be

apparently a continuous function due to the continuous range of pore capillaries in the

reservoir and will define, in fact, the capillary pressure-saturation relation. This

argument is frequently applied to consider the static case of water distribution above

the 100% water saturation level in the reservoir, under initial conditions, for which the

drainage capillary pressure curve is required. There will generally be no sharp interface

between the water and oil but, rather, a zone in which saturations decrease with height

above the 100% water saturation level, at which P

= 0, in accordance with the capillary

pressure (capillary rise)-saturation relationship. The vertical distance between the point

at which S

= 100%, P

= 0 and S

= S

is called the capillary transition zone and is

denoted by H.

This chapter is more concerned with the effect of capillary pressure on the

displacement of oil by water, for which the imbibition capillary pressure curve is

relevant (P

= 0 at S

= 1 − S

). Consider the static situation during a water drive

shown in fig. 10.5.

WATER

S = 1 - S

wor

z = y cos

1 - S

∆ρ

OIL

Fig. 10.5 Determination of water saturation as a function of reservoir thickness above

the maximum water saturation plane, S

= 1−

−−

−S

, of an advancing waterflood

IMMISCIBLE DISPLACEMENT 342

By static it is meant that the downdip water injection is stopped when the maximum

water saturation plane, S

= 1 − S

, at which P

= 0, has just reached point X in the

linear displacement path. If the imbibition capillary pressure curve has a distinct

capillary transition zone, as shown on the right hand side of the diagram, then above

point X the water saturation will be distributed in accordance with the capillary pressure

(capillary rise)-saturation relationship. In particular, the capillary pressure at point A, a

distance y above the base of the reservoir, in the dip-normal direction (normal to the

flow direction), can be calculated as

cw o w

P (S ) = p p = g cos

ργ

−∆ (10.4)

from which the saturation at point A can be determined from the capillary pressure

curve, as shown in fig. 10.5.

Equation (10.4) is referred to, in this text, as the capillary pressure equation expressed,

in this case, in absolute units. In Darcy units, which are used in this chapter to develop

theoretical arguments, the general equation becomes

gycos

P(S ) (atm)

1.0133 10

ρθ

∆

(10.5)

while in the field units defined in table 4.1, which are employed in the exercises

()

P S 0.4335 y cos (psi)

γθ

=∆ (10.6)

where ∆

is the difference between the water and oil specific gravities in the reservoir.

Allowing the S

= 1 − S

plane to rise incrementally in fig. 10.5 will result in a different

water saturation distribution, in the dip-normal direction, at point X in the displacement

path. This concept is applied in sec. 10.7 in which dynamic displacement is viewed as

a series of static positions of the S

= 1 − S

plane as the flood moves through the

reservoir, each position leading to a new water saturation distribution dictated by the

capillary pressure-saturation relationship.

b) Displacement generally occurs under conditions of vertical equilibrium

Coats

has qualitatively explained the concept of vertical equilibrium by drawing an

analogy with a simple problem in heat conduction. If one were trying to mathematically

describe heat conduction in a thin metal plate, say, 1/8th of an inch thick and with an

area of several square feet, no allowance would be made for the heat distribution

across the thickness of the metal, in which direction thermal equilibrium would be

assumed. Since reservoirs, typically, have dimensions in proportion to those described

for the metal plate, displacement problems can be frequently tackled in a similar

manner. In this case, however, the assumption made is that of fluid potential

equilibrium across the thickness of the reservoir.

The condition for fluid potential equilibrium is simply that of hydrostatic equilibrium,

discussed previously, for which the saturation distribution can be determined as a

function of capillary pressure and, therefore, height, as

IMMISCIBLE DISPLACEMENT 343

()

gycos

1.0133 10

∆

(10.5)

that is, the fluids are distributed in accordance with capillary-gravity equilibrium. The

vertical equilibrium condition can therefore be interpreted in the following manner.

When, during the displacement of oil by water, the water saturation at any point in the

reservoir increases by a small amount, the new water saturation is instantaneously

redistributed as indicated by equ. (10.5). This means that the vertical velocities of oil

and water, as the two are redistributed in accordance with capillary-gravity equilibrium,

appear to be infinite in comparison with the velocity of fluid movement parallel to the

reservoir bedding planes resulting from the Darcy or viscous forces.

The condition of vertical equilibrium will be promoted by

- a large vertical permeability (k

)

- small reservoir thickness (h)

- large density difference between the fluids (∆

)

- high capillary forces (large capillary transition zone H)

- low fluid viscosities

- low injection rates.

Coats

5,6

has presented two dimensionless groups, relating the above terms, the

magnitudes of which can be used as "rough rules of thumb" for deciding whether

vertical equilibrium conditions prevail in the reservoir. The two cases considered can

be applied when the capillary transition zone is large and also when it is negligible.

These dimensionless groups are not presented in this text since, irrespective of their

magnitude, the only way to check the validity of the vertical equilibrium is by using the

numerical simulation techniques described in sec. 10.10. In any case, when applying

simple, analytical techniques to describe the displacement process one is obliged to

assume that either vertical equilibrium is valid or else the complete opposite, that there

is a total lack of vertical equilibrium. The latter case will apply when, for instance, the

injection rate is so high that the water and oil velocities, parallel to the bedding planes

are much greater than their velocity components in the dip-normal direction. Under

these circumstances the water saturation will be uniformly distributed with respect to

thickness. These two extremes both represent conditions under which the saturation

profile in the dip-normal direction is definable and this facilitates the application of the

analytical techniques described in this chapter. For in-between cases the engineer

must resort to numerical simulation techniques (refer sec. 10.10). It has been found

that the vertical equilibrium condition is approximately satisfied in a great many

reservoirs. Nevertheless, it will be repeatedly stated throughout the remainder of the

chapter precisely when this condition is being assumed, and when not.

IMMISCIBLE DISPLACEMENT 344

c) The displacement is considered as incompressible

This assumption implies that steady state conditions prevail in the reservoir with the

pressure at any point remaining constant. There must, of course, be a pressure

differential between injection and production wells but the variation in the pressure

dependent variables, viscosities and densities, resulting from this differential is ignored.

This type of displacement will occur if

towi

qqq q=+= (10.7)

where

= total flow rate (r.vol/time)

= oil"""

= water"""

= water injection rate

The assumption is quite realistic since the engineer has control over the displacement

process to a much greater extent than, say, during the volumetric depletion of a

reservoir. Therefore, the wells and surface facilities are usually designed for constant

rate injection/production for it makes little sense to do otherwise. In addition, from a

reservoir engineering point of view, there are definite advantages in maintaining the

pressure at a constant level above that at which the solution gas first becomes mobile

(refer Chapter 3, sec. 5). Because of this assumption the methods described in this

chapter will be equally appropriate for the description of the displacement of oil by gas

at constant pressure with no mass transfer between the phases.

d) The displacement is considered to be linear

Throughout the chapter displacement will be considered exclusively in a linear

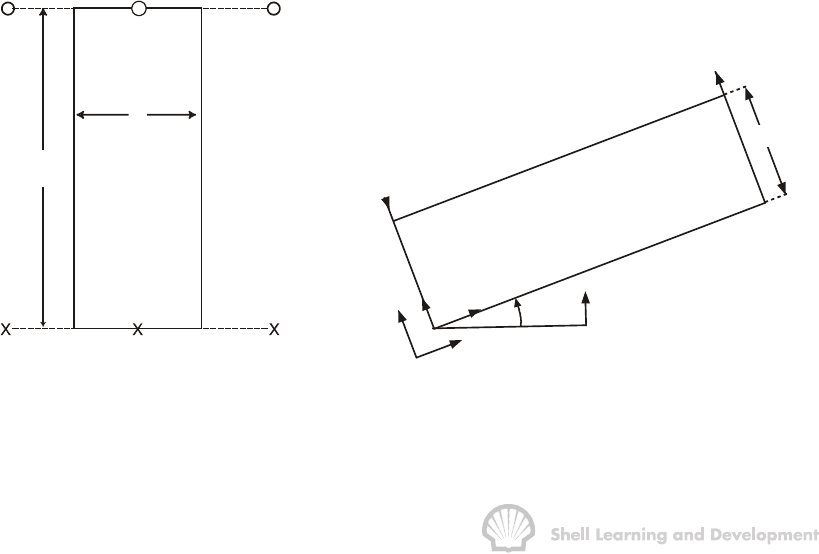
prototype reservoir model, as shown in fig. 10.6.

Injection

Production

(a) (b)

Fig. 10.6 Linear prototype reservoir model, (a) plan view; (b) cross section

IMMISCIBLE DISPLACEMENT 345

The model represents a symmetry element taken from a line drive pattern. The co-

ordinates used in describing displacement in the linear cross section are shown in

fig. 10.6(b). Both the injection and production wells are considered to be perforated

across the entire formation thickness, in the dip-normal direction. No account is taken

of the distortion of the linear flow streamlines (lines of constant fluid potential) in the

vicinity of the wells and saturations are assumed to be uniformly distributed across the

entire width of the block, that is, normal to plane shown in fig. 10.6(b).

The main concern in this chapter is, therefore, to account for the fluid saturation

distributions in the dip-normal direction (y-direction) as the flood moves through the

linear reservoir block. No analytical methods are presented to account for the areal

distribution of saturations in the reservoir. Such methods do exist for regular grid

spacings of injection and production wells and are described in the Craig monograph

For irregular well spacing, however, the analytical methods are extremely complex and

have largely been superseded by numerical simulation techniques. In fact, one of the

main purposes in using simulators is to determine the areal distribution of oil and water

(or displacing fluid in general) resulting from a flood. This knowledge enables the

engineer to place injection and production wells to gain the maximum recovery. To

provide such results, however, it is necessary that the simulator be informed of what

can be expected to occur in the dip-normal direction, that is, how the fluids will be

distributed in this direction. This information is generally provided as input to the

simulation.

The whole intent of this chapter is, therefore, to describe the physics governing

displacement, as viewed through a linear cross section of the reservoir, which is of vital

concern if the areal distributions of fluids are to be correctly modelled. The chapter

describes, in the first place, displacement in a homogeneous linear section,

secs. 10.3-7, and subsequently extends the methods developed to the description of

displacement in inhomogeneous (layered) reservoirs.

10.3 THE FRACTIONAL FLOW EQUATION

In this, and the following two sections, oil displacement will be assumed to take place

under the so-called diffuse flow condition. This means that fluid saturations at any point

in the linear displacement path are uniformly distributed with respect to thickness. The

sole reason for making this assumption is that it permits the displacement to be

described, mathematically, in one dimension and this provides the simplest possible

model of the displacement process. The one dimensional description follows from the

fact that since the water saturation is uniformly distributed in the dip-normal direction

then so too are the relative permeabilities to oil and water, which are themselves

functions of the water saturation at any point. This means that the simultaneous flow of

oil and water can be modelled using thickness averaged relative permeabilities, along

the centre line of the reservoir, which are also equivalent to relative permeabilities at

any point throughout the thickness.

IMMISCIBLE DISPLACEMENT 346

The diffuse flow condition can be encountered under two extreme physical conditions:

a) when displacement occurs at very high injection rates so that, as described in

sec. 10.2, the condition of vertical equilibrium is not satisfied and the effects of

the capillary and gravity forces are negligible, and

b) for displacement at low injection rates in reservoirs for which the measured

capillary transition zone greatly exceeds the reservoir thickness (H >> h) and the

vertical equilibrium condition applies.

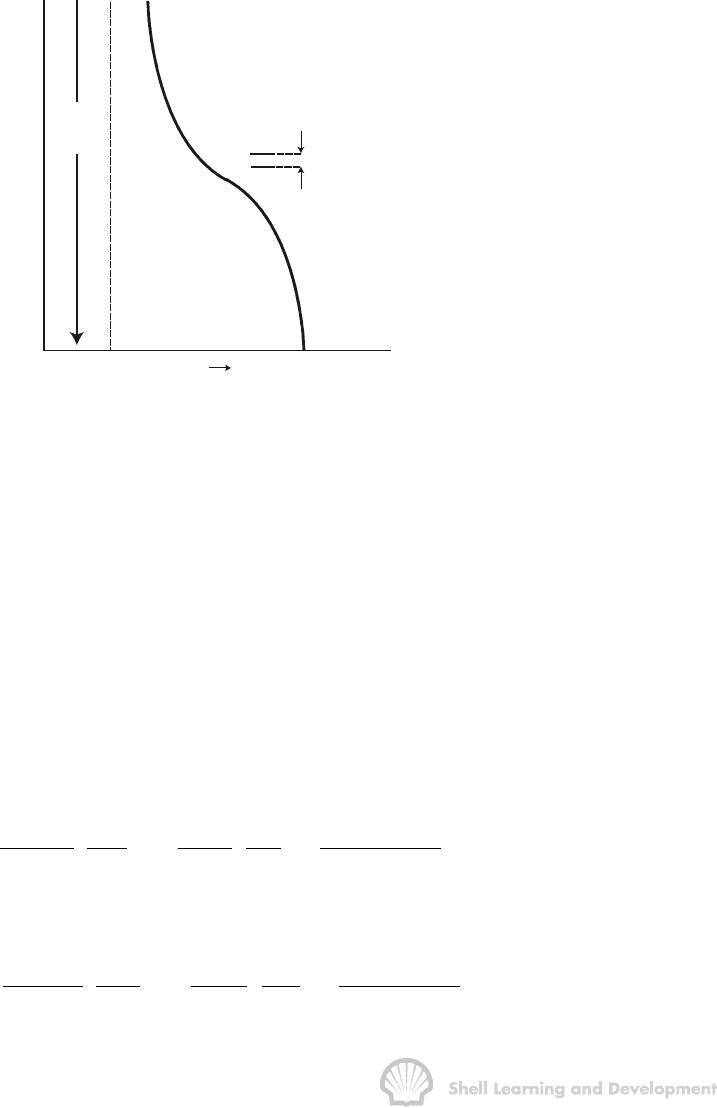
The latter case can be visualized by considering the capillary pressure curve, fig. 10.7.

Since, H >> h then it will appear that the water saturation is, to a first approximation,

uniformly distributed with respect to thickness in the reservoir.

1 - S

RESERVOIR THICKNESS h

Fig. 10.7 Approximation to the diffuse flow condition for H>> h

It should also be noted that relative permeabilities are measured in the laboratory

under the diffuse flow condition. This normally results from displacing one fluid by

another, in thin core plugs, at high flow rates

. As such, the laboratory, or rock relative

permeabilities, must be regarded as point relative permeabilities which are functions of

the point water saturation in the reservoir. It is, therefore, only when describing

displacement, under the diffuse flow condition, that rock relative permeabilities can be

used directly in calculations since, in this case, they also represent the thickness

averaged relative permeabilities.

Consider then, oil displacement in a tilted reservoir block, as shown in fig. 10.6(b),

which has a uniform cross sectional area A. Applying Darcy's law, for linear flow, the

one dimensional equations for the simultaneous flow of oil and water are

ro o o ro o o

kk A kk A p g sin

1.0133 10

ρρθ

µµ

∂Φ ∂

æö

=− =− +

ç÷

∂∂

èø

and

rw w w rw w w

kk A kk A p g sin

1.0133 10

ρρ

µµ

∂Φ ∂

æö

=− =− +

ç÷

∂∂

èø

IMMISCIBLE DISPLACEMENT 347

By expressing the oil rate as

= q

- q

the subtraction of the above equations gives

oto crw

rw ro ro

gsin

kk kk kk x 1.0133 10

µµµ

æö

∂

∆

æö

=− + = + −

ç÷

∂×

èø

(10.8)

in which

xx x

∂∂

∂

=−

∂∂ ∂

the capillary pressure gradient in the direction of flow, and

∆

The fractional flow of water, at any point in the reservoir, is defined as

ow t

qq q

and substitution of this in equ. (10.8) gives

ro c

row

rw o

kk A P

gsin

1.0133 10

∂

∆

æö

+−

ç÷

∂

èø

+⋅

(10.9)

while, by analogy with equ. (4.18), this equation can be expressed in field units as

ro c

row

rw o

kk A P

1 1.127 10 .4335 sin

−

∂

æö

+× − ∆

ç÷

∂

èø

+⋅

(10.10)

both of these being fractional flow equations for the displacement of oil by water, in one

dimension.

It is worthwhile considering the influence of the various component parts of this

expression. According to the convention adopted in this text

is the angle measured

from the horizontal to the line indicating the direction of flow. Therefore, the gravity

term ∆

g sin

/1.0133×10

will be positive for oil displacement in the updip direction

(0 <

), as shown in fig. 10.6(b), and negative for displacement downdip

(

< 2

). As a result, provided all the other terms in equ. (10.9) are the same, the

fractional flow of water for displacement updip is lower than for displacement downdip

since in the former case gravity tends to suppress the flow of water.

IMMISCIBLE DISPLACEMENT 348

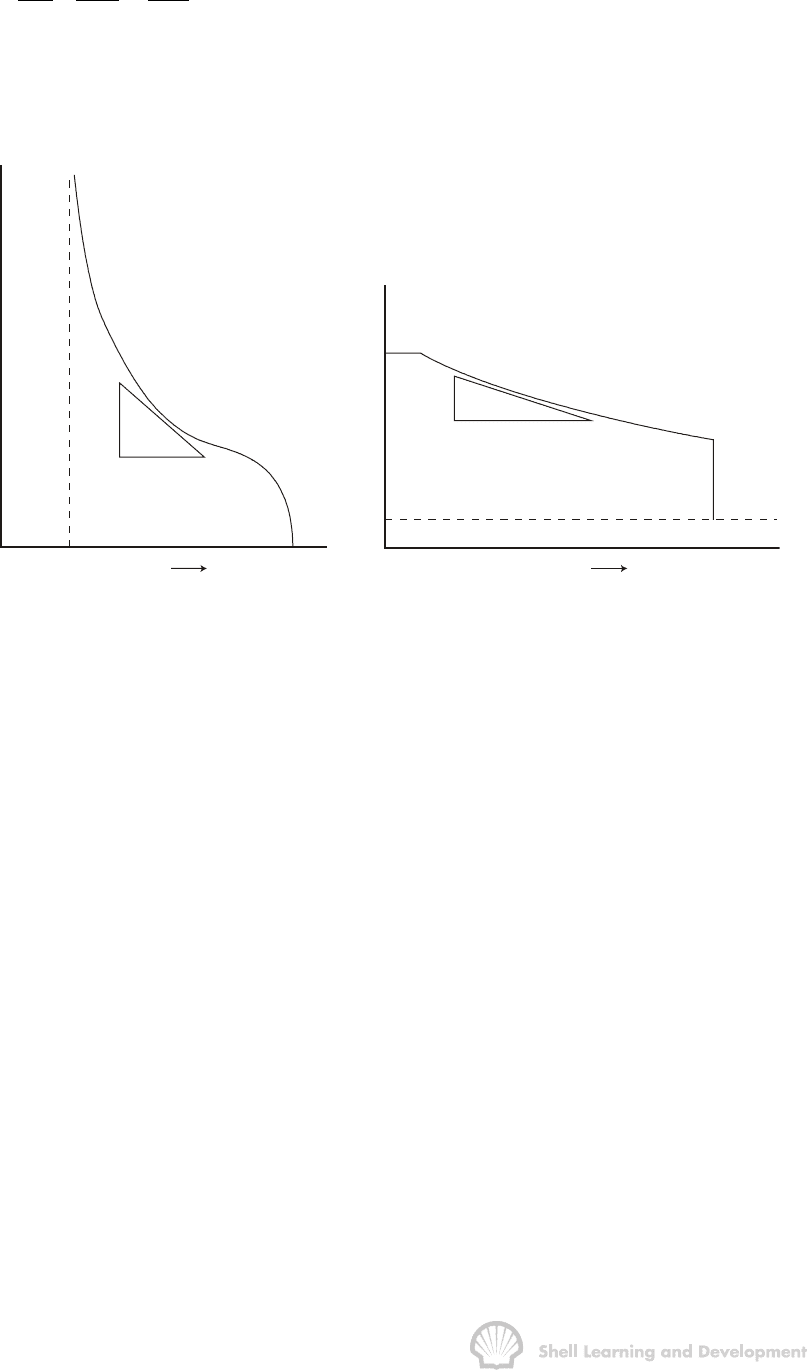
The effect of the capillary pressure gradient term is less obvious but can be

qualitatively understood by expressing the gradient as

cc w

PdP S

xdS x

∂∂

=⋅

∂∂

(10.11)

The first term on the right hand side is the slope of the capillary pressure curve,

fig. 10.8(a), and is always negative. The second term is the slope of the water

saturation profile in the direction of flow, a typical profile being shown in fig. 10.8(b).

1 - S

+dS

-dP

(a)

-dS

+dx

(b)

Fig. 10.8 (a) Capillary pressure function and; (b) water saturation distribution as a

function of distance in the displacement path

From this it can be seen that ∂S

/∂x is also negative. Therefore ∂P

/∂x is always

positive and consequently the presence of the capillary pressure gradient term tends to

increase the fractional flow of water. Quantitatively, it is difficult to allow for the capillary

pressure gradient for, although the capillary pressure curve may be available, the water

saturation profile, fig. 10.8(b), is unknown and, as will be shown presently, is the

required result of displacement calculations.

The water saturation distribution shown in fig. 10.8(b), corresponding to the situation

after injecting a given volume of water, may be regarded as typical for the

displacement of oil by water. The diagram shows that there is a distinct flood front, or

shock front, at which point there is a discontinuity in the water saturation which

increases abruptly from S

to S

, the flood front saturation. It is at this shock front

where both derivatives on the right hand side of equ. (10.11) have their maximum

value, which is evident by inspection of fig. 10.8(a) and (b), and therefore ∂P

/∂x is also

maximum. behind the flood front there is gradual increase in saturations from S

up to

the maximum value 1 - S

. In this region it is normally considered that both dP

/dS

and ∂S

/∂x are small and therefore ∂P

/∂x can be neglected in the fractional flow

equation.

For displacement in a horizontal reservoir (sin

= 0), and neglecting, for the moment,

the capillary pressure gradient, the fractional flow equation is reduced to

IMMISCIBLE DISPLACEMENT 349

rw o

+⋅

(10.12)

Provided the oil displacement occurs at a constant temperature then the oil and water

viscosities have fixed values and equ. (10.12) is strictly a function of the water

saturation, as related through the relative permeabilities. For a typical set of relative

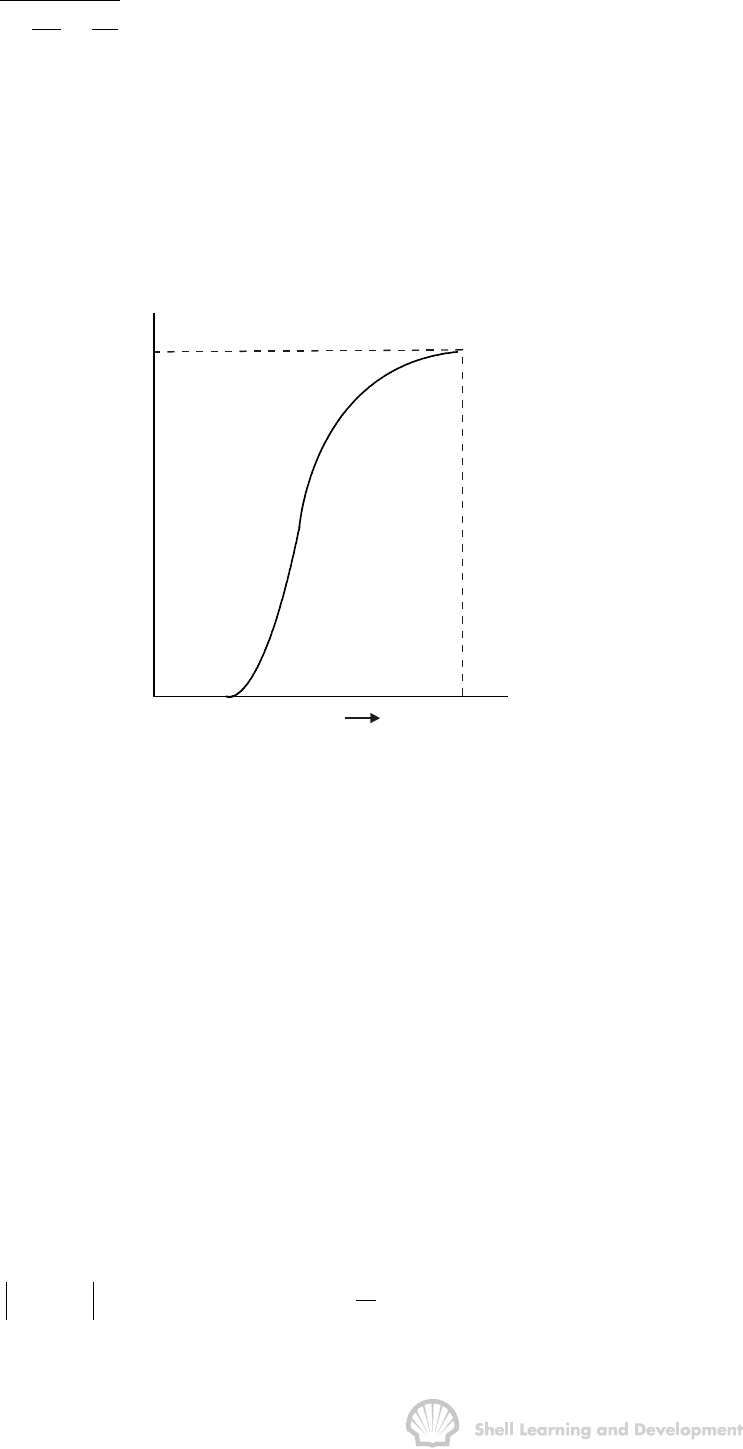
permeabilities, as shown in fig. 4.8, the fractional flow equation, (10.12), usually has

the shape indicated in fig. 10.9, with saturation limits S

and 1 − S

, between which

the fractional flow increases from zero to unity. The manner in which the shape of this

curve is influenced by the viscosity ratio of oil to water will be studied in exercise 10.1.

1 - S

f= 1

Fig. 10.9 Typical fractional flow curve as a function of water saturation, equ. (10.12)

The fractional flow equation is used to calculate the fraction of the total flow which is

water, at any point in the reservoir, assuming the water saturation at that point is

known. Precisely how to determine when a given water saturation plane reaches a

particular point in the linear system requires the application of the displacement theory

presented in the following section.

10.4 BUCKLEY-LEVERETT ONE DIMENSIONAL DISPLACEMENT

In 1942 Buckley and Leverett presented what is recognised as the basic equation for

describing immiscible displacement in one dimension

. For water displacing oil, the

equation determines the velocity of a plane of constant water saturation travelling

through a linear system. Assuming the diffuse flow condition, the conservation of mass

of water flowing through volume element

Adx,

fig. 10.10, may be expressed as

Mass flow rate = Rate of increase of mass

In - Out in the volume element

ww ww ww

xdx

qq Adx(S)

ρρ φρ

∂

−=

∂

(10.13)

IMMISCIBLE DISPLACEMENT 350

q |

x+dx

Fig. 10.10 Mass flow rate of water through a linear volume element Adx

ww ww ww ww

qq (q)dxAdx(S)

ρρ ρφρ

∂∂

æö

−+ =

ç÷

∂∂

èø

which can be reduced to

ww ww

(q ) A ( S )

ρφρ

∂∂

=−

∂∂

(10.14)

and for the assumption of incompressible displacement (

≈ constant)

∂∂

=−

∂∂

(10.15)

The full differential of the water saturation is

dS dx dt

∂∂

and since it is the intention to study the movement of a plane of constant water

saturation, that is, dS

= 0, then

xtS

SSdx

txdt

∂∂

=−

∂∂

(10.16)

Furthermore,

www

qqS

xSx

æö

∂∂∂

=⋅

ç÷

∂∂∂

èø

(10.17)

and substituting equs. (10.16) and (10.17) in equ. (10.15) gives

qdx

Sdt

∂

(10.18)

Again, for incompressible displacement, q

is constant and, since q

= q

, equ. (10.18)

may be expressed as