Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

339

Mechanical Pr

7. Mechanical Properties

Materials used in engineering applications as

structural components are subject to loads,de-

ﬁned by the application purpose. The mechanical

properties of materials characterize the response

of a material to loading.

The mechanical loading action on materials

in engineering applications may be static or dy-

namic and can basically be categorized as tension,

compression, bending, shear, and torsion. In ad-

dition, thermomechanical loading effects can occur

(Chap. 8). There may also be gas loads from the

environment, leading to gas/materials interac-

tions (Chap. 6) and to transport phenomena such

as permeation and diffusion.

The mechanical loading action and the corre-

sponding response of materials can be illustrated

by the well-known stress–strain curve (for def-

inition see Sect. 7.1.2). Its different regimes and

characteristic data points characterize the me-

chanical behavior of materials treated in this

chapter in terms of elasticity (Sect. 7.1), plasticity

(Sect. 7.2), hardness (Sect. 7.3), strength (Sect. 7.4),

and fracture (Sect. 7.5). Methods for the determi-

nation of permeation and diffusion are compiled

in Sect. 7.6.

7.1 Elasticity.............................................. 340

7.1.1 Development of Elasticity Theory.... 340

7.1.2 Deﬁnition of Stress and Strain,

and Relationships Between Them .. 341

7.1.3 Measurement of Elastic Constants

in Static Experiments .................... 344

7.1.4 Dynamic Methods

of Determining Elastic Constants .... 349

7.1.5 Instrumented Indentation

as a Method of Determining

Elastic Constants .......................... 352

7.2 Plasticity.............................................. 355

7.2.1 Fundamentals of Plasticity ............ 355

7.2.2 Mechanical Loading Modes Causing

Plastic Deformation ...................... 357

7.2.3 Standard Methods

of Measuring Plastic Properties ...... 358

7.2.4 Novel Test Developments

for Plasticity ................................ 365

7.3 Hardness ............................................. 366

7.3.1 Conventional Hardness Test

Methods (Brinell, Rockwell, Vickers

and Knoop) ................................. 368

7.3.2 Selecting a Conventional Hardness

Test Method and Hardness Scale .... 374

7.3.3 Measurement Uncertainty in

Hardness Testing (HR, HBW, HV, HK) 376

7.3.4 Instrumented Indentation Test (IIT) 378

7.4 Strength .............................................. 388

7.4.1 Quasistatic Loading ...................... 389

7.4.2 Dynamic Loading ......................... 398

7.4.3 Temperature

and Strain-Rate Effects ................. 401

7.4.4 Strengthening Mechanisms

for Crystalline Materials ................ 402

7.4.5 Environmental Effects................... 404

7.4.6 Interface Strength:

Adhesion Measurement Methods ... 405

7.5 Fracture Mechanics ............................... 408

7.5.1 Fundamentals

of Fracture Mechanics ................... 408

7.5.2 Fracture Toughness....................... 410

7.5.3 Fatigue Crack Propagation Rate...... 419

7.5.4 Fractography ............................... 424

7.6 Permeation and Diffusion ..................... 426

7.6.1 Gas Transport:

Steady-State Permeation .............. 427

7.6.2 Kinetic Measurement.................... 429

7.6.3 Experimental Measurement

of Permeability ............................ 431

7.6.4 Gas Flux Measurement .................. 433

7.6.5 Experimental Measurement

of Gas and Vapor Sorption............. 436

7.6.6 Method Evaluations...................... 440

7.6.7 Future Projections ........................ 442

References .................................................. 442

Part C 7

340 Part C Materials Properties Measurement

7.1 Elasticity

Elastic properties of materials must be obtained by ex-

periment methods. Materials are too complicated and

theories of solids insufﬁciently sophisticated to obtain

accurate theoretic determinations of elastic constants.

Usually, simple static mechanical tests are used to eval-

uate the elastic constants. Specimens are either pulled

in tension, squeezed in compression, bent in ﬂexure or

twisted in torsion and the strains measured by a variety

of techniques. The elastic constants are then calculated

from the elasticity equation relating stress to strain.

From these measurements, Young’s modulus, Poisson’s

ratio and the shear modulus are determined. These

are the moduli commonly used for the calculation of

stresses or strains in structural applications. More ac-

curate than the static method of determining the elastic

constants are the dynamic techniques that have been de-

veloped for this purpose. In these techniques a bar is set

into vibration and the resonant frequencies of the bar are

measured. A solution of the elastic equations for the vi-

bration of a bar yields a relationship between the elastic

constants, the resonant frequencies and the dimensions

of the bar. These techniques are about ﬁve times as

accurate as the static techniques for determining the

elastic constants. Elastic constants can also be meas-

ured by determining the time of ﬂight of an elastic wave

through a plate of given thickness. Because there are

two kinds of waves that can traverse the plate (longitu-

dinal waves and shear waves), the two elastic constants

required for structural calculations can be determined

independently. Finally, the newest advances in tech-

niques for measuring the elastic constants of materials

have their origins in the need to measure these con-

stants in thin ﬁlms, or parts too small to be determined

independently. The development of nanoindentation de-

vices proves to be ideal for the measurement of elastic

constants in these kinds of materials. Each of these

techniques is discussed in terms of standard American

Society for Testing and Materials (ASTM) and inter-

national test methods that were developed to assure

repeatability and reliability of testing. This discussion

serves as a primer for engineers and scientists wanting

to determine the elastic constants of materials.

7.1.1 Development of Elasticity Theory

The design of new components for structural applica-

tions usually includes an analysis of stress and strain to

assure structural reliability. Two general kinds of prac-

tical problems are encountered: the ﬁrst in which all

of the forces on the surface of a body and the body

forces are known; the second in which the surface dis-

placements on the body are prescribed and the body

forces are known [7.1]. In both cases, calculation of the

stresses and displacements throughout the body and at

the body surface is the objective. Within the limits of

an elastic material, i. e., a material in which the dis-

placements and stresses completely disappear once all

of the constraints are removed, the theory for solving

such problems was completely developed by the end

of the 19th century. There are many methods of solv-

ing such problems, especially with the development of

ﬁnite element analysis. All such problems require the

elastic constants of the material of interest as an input

in order to obtain a solution. The description of experi-

mental techniques of measuring the elastic constants of

engineering materials are the main subject of this chap-

ter, but before describing the experimental techniques,

we ﬁrst give a brief history of the development of the

theory of elasticity. We then go on to describe the theory

of elasticity in order to put our later discussion of exper-

imental techniques into context. There are several good

books or chapters in books that give a history of the the-

ory of elasticity [7.1–3], and there are many excellent

texts that describe the theory [7.1, 4]. The discussion

given below rests heavily on [7.1–4].

The ﬁrst scientist to consider the strength of mater-

ials was Galileo in 1638 with his investigation of the

strength of a rigid cantilever beam under its own weight,

the beam being imbedded in a wall at one end [7.5]. He

treated the beam as a rigid solid and tried to determine

the condition of failure for such a beam. The concepts

of stress and strain were not yet developed, nor was it

known that the neutral axis should be in the middle of

the beam. The solution he obtained was not correct; nev-

ertheless, his worked stimulated other scientists to work

on the same problem.

The next important contributor to the theory of elas-

ticity was Hooke in 1678, when he discovered the law

that has been subsequently named after him [7.6]. He

found that the extension of a wide variety of springs

and spring-like materials was proportional to the forces

applied to the springs. This ﬁnding forms the basis of

the theory of elasticity, but Hooke did not apply the dis-

covery to material problems. A few years later (1680),

Mariotte announced the same law and used it to under-

stand the deformation of the cantilever beam [7.7]. He

argued that the resistance of a beam to ﬂexural forces

should result from some of the ﬁlaments of the beam

Part C 7.1

Mechanical Properties 7.1 Elasticity 341

being put into tension, the rest being put into compres-

sion. He assigned the neutral axis to one-half the height

of the beam and used this assumption to correctly solve

the force distribution in the cantilever beam. Young fur-

ther developed Hooke’s law in 1807 by introducing the

idea of a modulus of elasticity [7.8,9]. Young’s modulus

was not expressed simply as a proportionality constant

between tensile stress and tensile strain. Instead, he de-

ﬁned the modulus as the relative diminution of the length

of a solid at the base of a long column of the solid. Nev-

ertheless, his contribution was used in the development

of general equations of the theory of elasticity.

The ﬁrst attempt to develop general equations of

elastic equilibrium was by Navier, whose model was

based on central-force interactions between molecules

of a solid [7.10]. He developed a set of differen-

tial equations that could be used to calculate internal

displacements in an isotropic body. The form of the

equations was correct, but because of an oversimpliﬁca-

tion of the force law, the equations contained only one

elastic constant.

Stimulated by the work of Navier, Cauchy in 1822

developed a theory of elasticity that contained two elas-

tic constants and is essentially the one we use today

for isotropic solids (presented to the French Academy

of Sciences on Sept. 30, 1822; Cauchy published the

work in his Excercices de mathématique, 1827 and

1828. See footnote 32 in the ﬁrst chapter of [7.3]). For

nonisotropic solids, many more elastic constants are

needed, and for a long time an argument raged over

whether the number of constants for the most general

type of anisotropic material should be 15 or 21. The

controversy was settled by experiments that were car-

ried out on single crystals with pronounced anisotropy,

which showed that 21 is the correct number of constants

in the most anisotropic elastic case. This number is also

supported by crystal symmetry theory.

Once the theory of elasticity was completely devel-

oped, equations could then be derived for experimental

measurement of the elastic constants. This has now

been done quite generally so that the techniques that

have been developed have a good scientiﬁc basis in the

theory of elasticity. Elastic constants can be measured

statically (tension, compression, torsion or ﬂexure), or

dynamically through the study of vibrating bars, or by

measuring the velocity of sound through the material.

Most of these measurements are made on materials that

are isotropic, so that only two constants are determined;

however, with the development of composite materials

for structural members, isotropy is lost and other con-

stants have to be considered.

7.1.2 Deﬁnition of Stress and Strain,

and Relationships Between Them

The theory of linear elasticity begins by deﬁning stress

and strain [7.1, 3, 4]. Stress gives the intensity of the

mechanical forces that pass through the body, whereas

strain gives the relative displacement of points within

the body. In the theory of linear elasticity, stress and

strain are related by the elastic constants, which are ma-

terial properties. In this section we deﬁne and discuss

stress and strain and show how they are related through

the elastic constants. It is these elastic constants that

must be determined in order to evaluate stress distribu-

tions in structural components.

Stresses

When a body is under load by external forces, internal

forces are set up between different parts of the body.

The intensities of these forces are usually described by

the force per unit area on the test surface through which

they act. One can imagine cutting a small test surface

within a material and replacing the material on one side

of the surface by forces that would maintain the posi-

tion of the surface in exactly the same position as it was

before the cut was made. As the size of the test surface

is diminished to zero, the sum of the forces on the sur-

face divided by the area of the surface is deﬁned as the

magnitude of the stress on the surface. The direction of

the stress is given by the direction of the force on the

surface and need not be normal to the surface.

From the deﬁnition of stress, it is clear that the stress

on a surface will vary with orientation and position of the

surface within the solid. It is also usual to break down

the components of stress into stresses normal and paral-

lel to the surface. The stresses parallel to the surface are

called shear stresses. Because stress depends on both the

orientation of the surface, and the direction of the forces

on the surface, the symbol indicating stress will have two

subscripts attached to it, the ﬁrst indicating the surface

normal, the second indicating the direction of the forces

on the surface. Consider a Cartesian coordinate system

with three mutually perpendicular axes, x

, x

,andx

Atestsurfacenormaltothe x

-axiswillhavestresses,σ

,andσ

, where σ is the symbol for stress. The force

indicated by the stress σ

is on the x

-surface,and its ori-

entation is parallel to the x

-axis. The stress σ

is either

a tensile stress (positive sign by convention), or a com-

pressive stress (negative sign). The stresses, σ

and σ

are shear stresses: σ

beingonthex

-surface and ori-

entedinthex

-direction; σ

being on the x

-surface and

oriented in the x

-direction.

Part C 7.1

342 Part C Materials Properties Measurement

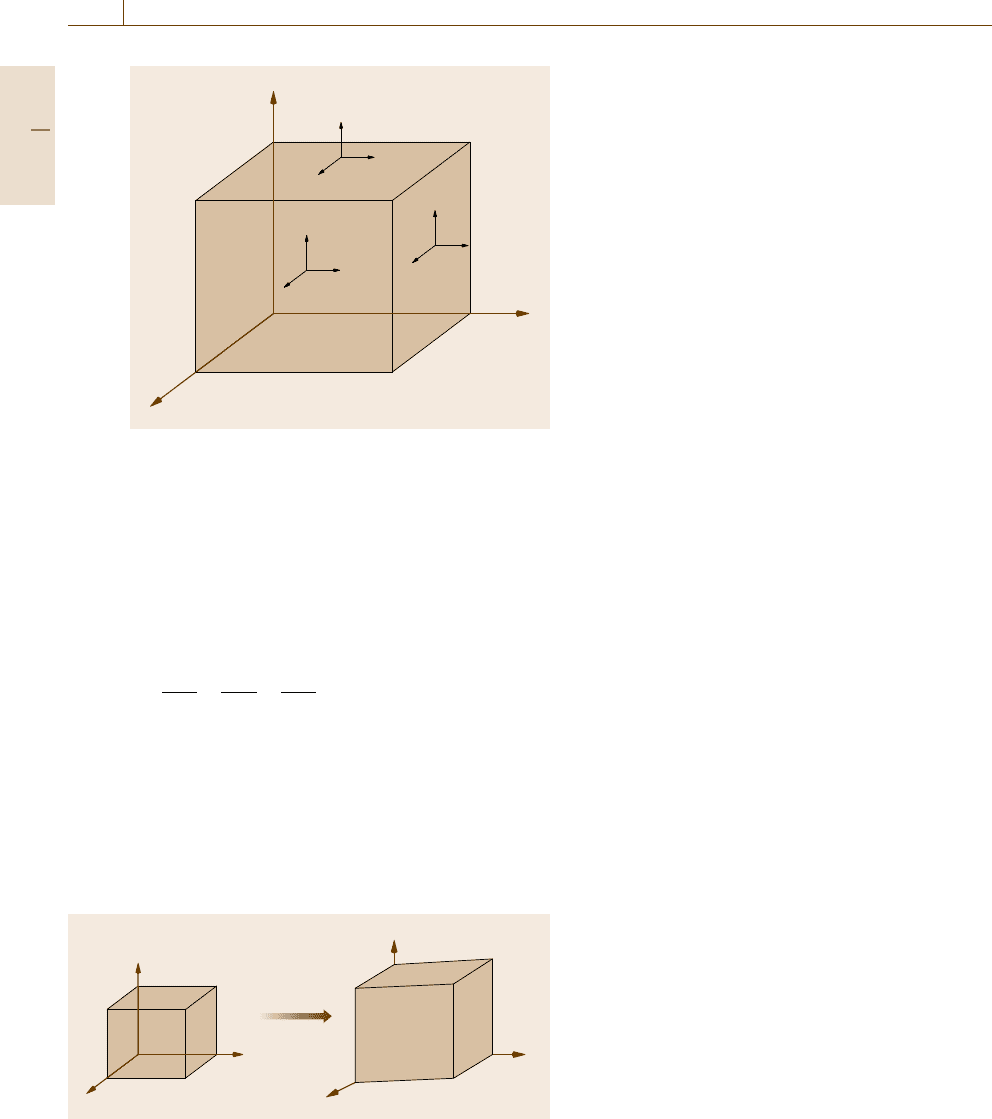
Fig. 7.1 Illustration of the two-index notation of stress.

Stresses on the negative side of the cube have the opposite

direction to those on the front side. Stresses in the ﬁgure

are all positive

An example of the stresses oriented around a small

cube is shown in Fig. 7.1. From the fact that the cube is

in equilibrium, the equation of equilibrium can be deter-

mined. Summing up the forces in the x

-direction, the

following equation is obtained

∂σ

∂x

∂σ

∂x

∂σ

∂x

=0 , (7.1)

where F

are the body forces in the x

-direction. Similar

equations are found for the x

-andx

-axes.

A convenient shorthand representation has been de-

veloped for equations similar to (7.1). The subscripts

of (7.1) are indicated by lower-case letters, usually i, j,

and k. A partial derivative is indicated by a comma; a re-

peated index indicates a summation. Thus, (7.1) can be

Fig. 7.2 On deformation, the size of the box has increased and the

angles between the sides are no longer right angles, indicating both

a tensile and a shear strain

represented by

ij, j

=0 . (7.2)

Assignment of the value of 1, 2 and 3 for i yields three

independent equations for equilibrium. The body forces

may be constant, or a function of space and time.

The state of equilibrium for the cube in Fig. 7.1 can

also be used to prove that σ

= σ

.Takingthemo-

ment of the forces about a cube corner parallel to the

-axis, σ

σ dx

(dx

) =σ

σ dx

(dx

), which

yields σ

=σ

. Similar equations are obtained around

the x

-andx

-axis, proving the assertion that σ

=σ

Therefore, of the nine possible stress components at any

point within a body that is subjected to external forces,

only six of them are independent.

Strains

Strains are determined by the relative displacements of

points within a body that has been subjected to exter-

nal forces. Imagine a volume within the body that was

a cube prior to deformation, but has now been deformed

into a general hexahedron, the axes of which may not be

of equal length, or the angles between them right angles

(Fig. 7.2). Two types of strain can be deﬁned from this

ﬁgure: tensile strain, in which the length of the axes of

the cube have been changed by deformation, and a shear

strain, in which the angle between the axes of the cube

have been changed by the deformation. If u represents

the displacement in the x

-direction of any point within

the body due to the application of a set of forces, then

the displacement of an adjacent point a distance dx

away from the ﬁrst in a direction deﬁned by the x

axis is given by u +(∂u/∂x

)dx

. The relative change

between the two points in the x

-direction is ∂u/∂x

which is deﬁned as the tensile strain in the x

-direction,

. Similar deﬁnitions are used for the tensile strain

in the x

-andx

-directions: ε

and ε

. In this case,

v and w are the displacements in the y-andz-directions,

respectively.

The shear strains are deﬁned by the change in angle

of the cube corners. Projecting the cube onto an x

–x

plane (Fig. 7.3), the change in the angle of the cube

is given by ∂v/∂x

+∂w/∂x

, where v and w are the

displacements in the x

-andx

-direction, respectively.

The strain ε

is deﬁned by ε

=(∂v/∂x

+∂w/∂x

)/2.

Similar equations are obtained for ε

and ε

. As with

the shear components of the stress tensor ε

= ε

,as

can be seen from the deﬁnition of shear strain.

Some other properties of stress and strain are com-

mented on without proof. Both stress and strain are

tensor quantities and transform as tensors with the rota-

Part C 7.1

Mechanical Properties 7.1 Elasticity 343

tion of system axes. Consider a transformation of axes

from x

, x

to x

, x

, then the stresses will

transform according to the following equation

αβ

αi

β j

, (7.3)

where l

αi

and l

β j

are the cosines of the angles between

and x

,andx

and x

, respectively. Once the σ

are obtained at a point for a given set of axes, they can

be obtained for any other set of axes using this simple

transformation.

Stress–Strain Relations

Finally we arrive at the set of equations that relate stress

and strain. Since there are six independent components

to the stress tensor and six independent components to

the strain tensor, there will be 36 constants of propor-

tionality connecting the two

ijkl

. (7.4)

The coefﬁcients C

ijkl

are the elastic stiffness constants.

The repeat of the index kl in the subscripts on the

right-hand side of this equation indicate by convention

a summation over these subscripts for k =1, 2 and 3 and

similarly for l. Thus, for each of the six stress compo-

nents on the left-hand side of the equation, there are six

terms on the right-hand side and six coefﬁcients C

ijkl

Of the 36 constants, it can be shown by strain-energy

considerations that only 21 are independent. This num-

ber is reduced further by the symmetry of the solid. For

a cubic material, the number of elastic constants is re-

duced from 21 to three. For an isotropic material, the

v + dv/dx

w + dw/dx

Fig. 7.3 As can be seen from the ﬁgure, the angle between

the x

-andthex



-axes is 1/2(dw/ dx

+ dv/ dx

), as for

the x

- and x



-axes. This angle is deﬁned as the shear strain

=ε

(after [7.2])

number of elastic constants is two. Equation (7.4)may

be rewritten so that strain is expressed as a function

of stress, in which case the two tensors are related by

a set of constants S

ijkl

known as the elastic compliances.

The stiffness C

ijkl

and the compliance S

ijkl

are both

fourth-order tensors that depend on the axis orientation

for their values. They both transform as fourth-order

tensors

αβγδ

αi

β j

γ k

δl

ijkl

(7.5)

with a similar equation for the compliances.

Since most engineering materials are isotropic, it

is worth expanding the stress–strain equation (7.4)into

a form that has more practical signiﬁcance. The elastic

constants that are most commonly used are the Young’s

modulus E (the ratio of the tensile stress to the tensile

strain), the shear modulus μ (the ratio of the shear stress

to the shear strain), and the Poisson’s ratio ν (the ratio of

the strain parallel to the tensile axis to the strain normal

to the tensile axis). Since only two of these are indepen-

dent for an isotropic material, it can be shown that the

following relationship between the three exists

μ =

2(1+ν)

. (7.6)

Strain can be expressed in terms of stress for an

isotropic material, by the following equation

1+ν

−

Θ, (7.7)

where δ

is the Kronecker delta; it equals one for i = j

and zero otherwise. The term Θ is equal to σ

,which

indicates the sum over the subscript (σ

=σ

+σ

). When expanded (7.7) yields six equations, one for

each of the strain terms.

A similar equation can be written for stresses in

terms of strains; in which case, the most appropriate

elastic constants are the shear modulus μ and the Lamé

constant λ

=λε

·δ

+2με

. (7.8)

The Lamé constant can be expressed in terms of the

other elastic constants by

λ =

Eν

(1 +ν)(1 −2ν)

. (7.9)

Most of this article deals with the evaluation of Young’s

modulus, the shear modulus, and Poisson’s ratio, since

these are the ones most often used in practical applica-

tions, and hence, are the ones for which the standards

are written.

Part C 7.1

344 Part C Materials Properties Measurement

Linear elastic solutions of boundary problems can

be obtained using the relationships between stress and

strain (7.7) or its inverse (7.8) and the equations of

equilibrium (7.2) subject to the conditions at the bound-

ary. The solutions must satisfy a set of six equations

known as the compatibility relations. These equations

assure that solutions obtained yield valid displacement

ﬁelds, i.e. ﬁelds in which the body contains no voids or

overlapping regions after deformation.

The experimental conﬁgurations normally used to

determine the elastic constants are cylinders of cir-

cular or rectangular cross sections, which are loaded

in tension, ﬂexure or torsion. Under static loading,

elastic moduli are calculated from the load on the spec-

imen, a measurement of specimen displacement and an

elastic solution for the particular specimen. Measure-

ments can also be made by dynamic techniques that

involve resonance, or the time of ﬂight of an elastic

pulse through the material. In general, the static tech-

nique yielded results that are not as accurate as those

obtained dynamically, differing by about −5to+7%

of the mean value of the dynamic technique [7.11].

The difference may be due to a combination of ef-

fects (adiabatic versus isotropic conditions, dislocation

bowing, other sources of inelasticity, and different

levels of accuracy and precision). This is discussed

in Sect. 7.1.4.

In the remainder of this chapter, the techniques for

determining the elastic constants for isotropic materials

are discussed. The most recent ASTM recommended

tests will form the basis of the discussion. The standards

that are currently in use will be described and their ap-

plication to a given material will be discussed. Since

materials have a wide range of values for their elas-

tic properties, given standards are not suitable for all

materials. So, in the course of the discussion, the stan-

dards will be discussed with reference to the different

classes of materials (polymers, ceramics, and metals)

and recommendations will be made as to which tech-

nique is preferred for a given material. The relative error

of each standard measurement will also be discussed

with reference to the various materials.

Although ASTM tests are used in our discussions,

we recognize that these standards are not universal.

Other countries use different sets of standards. Never-

theless, the standards for elastic constants are all based

on the same set of elastic equations and the same physi-

cal principals. So, regardless of which standard is used,

the investigator should obtain identical results within

experimental scatter. Furthermore, the same material

considerations have to be taken into account in es-

tablishing a standard measurement technique. So here

too, the standard tests will have to be similar to ob-

tain a given accuracy. A list of European standards is

given in the appendix for those readers who prefer to

use standards other than ASTM.

Five general tests are used to determine the elas-

tic constants of materials. Tensile testing employing

a static load is used to measure Young’s modulus, and

Poisson’s ratio. Torsion testing of tubes or rods is used

to determine the shear modulus. Flexural testing under

a static load is used to determine Young’s modulus. Var-

ious geometries are used for the ﬂexural tests. Finally,

resonant vibration of long thin plates and the time of

ﬂight of sonic pulses are both used to measure Young’s

modulus and the shear modulus.

7.1.3 Measurement of Elastic Constants

in Static Experiments

In principal the simplest test geometry for determin-

ing elastic constants is the tensile test. A ﬁxed load is

placed on the ends of the specimen and the displace-

ment over a ﬁxed portion of gage section is measured.

The load divided by the cross-sectional area gives the

stress and the displacement divided by the length over

which displacement was measured gives the strain. The

Young’s modulus is then given by the stress divided by

the strain. Often, the Young’s modulus is measured as

part of a test carried out to determine the plastic prop-

erties of the metal. In such a test, a stress–strain curve

is obtained on the metal, and the linear portion of the

curve at the beginning of the test is used to calculate

the Young’s modulus. At the same time, if the lateral di-

mensions of the specimen are measured during the test,

the test results can be used to determine Poisson’s ratio

as a function of strain.

Test Specimens

Tensile tests are generally carried out on a universal

test machine. The precautions needed to achieve high

measurement accuracy include alignment of the test ma-

chine, calibration of the load cell, ﬁrm attachment of

the extensometers used to measure strain, and accu-

rate measurement of the dimensions of the specimen

cross section. Examples of specimen types and shapes,

and methods of gripping used in these machines are

showninFig.7.4 [7.12]. The type of specimen depends

on the stock from which the specimen is taken. Sheet

materials are usually tested in the form of ﬂat speci-

mens that are clamped with wedge grips on their ends.

The ﬂat specimens may also be pinned as well as be-

Part C 7.1

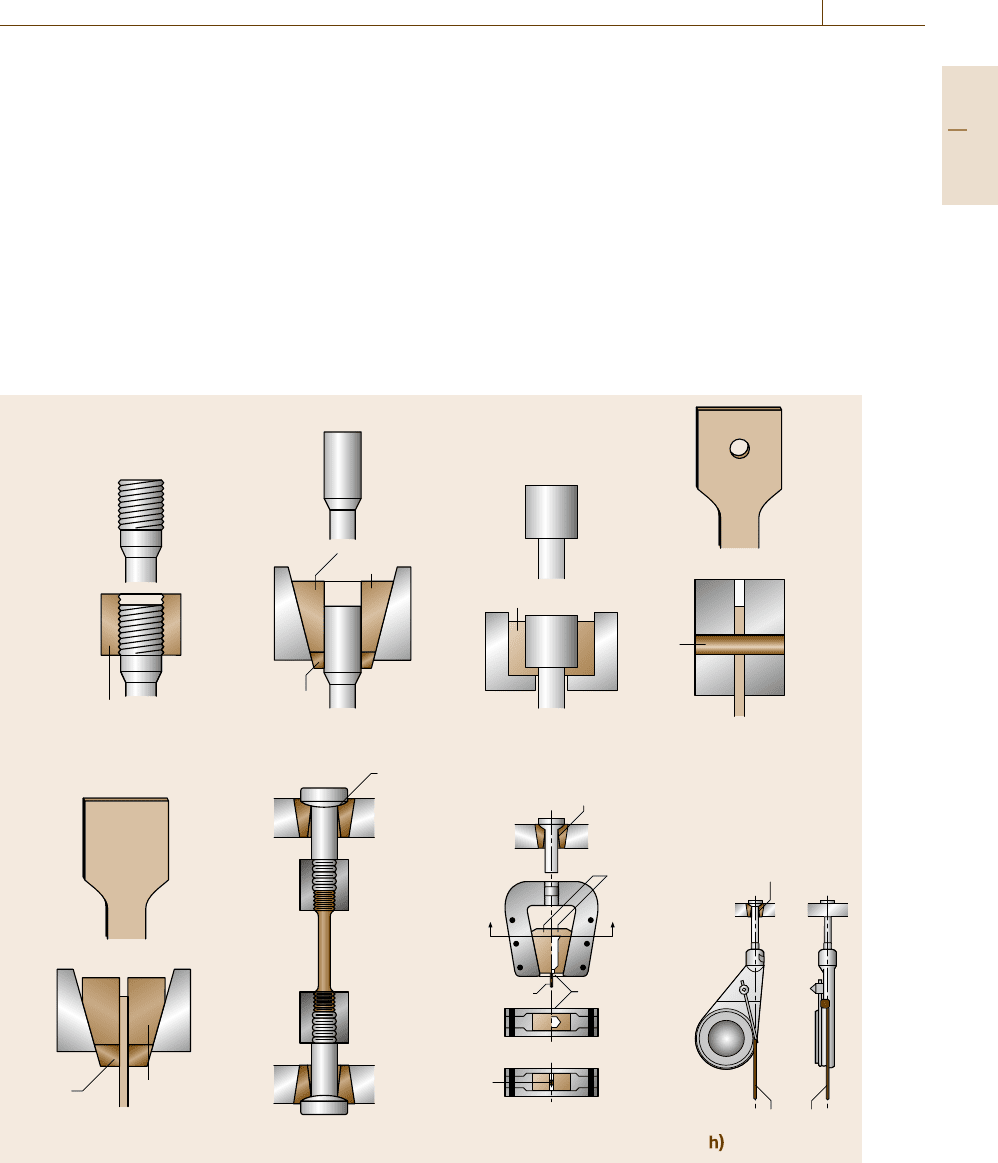
Mechanical Properties 7.1 Elasticity 345

ing clamped. Round stock is tested with threaded-end

or shoulder-end specimens that have matching shoul-

ders or threads on the gripping device. Wires are tested

using special snubbing devices in which the wire is

wound around a mandrel to add the load gradually

to the wire and thus prevent stress concentrations that

will reduce the measured strength (in a strength test).

In all specimens but the wires, the gage section is re-

duced to decrease the stress at the gripping points.

Finally, the grips are usually attached to the testing

machine through universal joints that prevent bending

of the specimen during loading. Speciﬁc criteria for

specimen dimensions and shapes are given in ASTM

E8[7.12].

Thread grip

Note:

Bad practice

Note:

Bad practice

Serrated

wedges

Outer

holding

ring

Split

collar

Spherical bearing

Specimen

Specimen with

threaded ends

Upper head

of testing

machine

Specimen

Section A–A for wire

Section A–A for sheet and strip

Cylindrical seat

Serrated faces

on grips

Cross-head of

testing machine

Spherical

bearing

Spherical

bearing

Serrated

wedges

e) f) g)

b) c) d)

Fig. 7.4a–h Specimen types and shapes, and methods of gripping specimens in a universal testing machine (after [7.12])

Test Forces

Forces are determined by electronic load cells that at-

tach to the testing machine and these can be calibrated

through dead-weight testing through the use of elastic

proving rings, or by the use of calibration strain-gage

load cells following the recommendations of ASTM

E74[7.13]. To assure that the load cell is operating cor-

rectly calibrations should be done periodically. Proving

rings and load cells are both portable, however the lat-

ter tend to be smaller, especially for large-scale loads

and so are often preferred. Regardless which device is

used, they in turn should be calibrated according to the

procedures in ASTM E 74. The calibration of load cells

on universal test machines should be checked each time

Part C 7.1

346 Part C Materials Properties Measurement

the machine is run, and periodic veriﬁcations of the load

system should be carried out using ASTM E4[7.14].

The required practice is to verify the test system one

year after the ﬁrst calibration and after that a minimum

of once every 18 months.

Strain Measurement

Strain on tensile specimens can be measured by the use

of extensometers that attach directly to the gage sec-

tion of the test specimen, by the use of strain gages

that are mounted directly to the specimen, or by the use

of optical systems, which directly sense the motion of

marks on the gage section or ﬂags attached to the gage

section of the tensile specimen. Clip-on extensometers

have knife-edges that press into the specimen surface

and clearly deﬁne the length of the gage section. They

are inherently more accurate than other techniques and

hence are used in standard methods for determining the

elastic constants [7.18].

Two basic kinds of clip-on extensometers are used

to detect strain. One contains a linear variable differ-

ential transformer (LVDT) that moves as a consequence

of specimen deformation and produces an electrical sig-

nal that is proportional to the motion. These are small,

lightweight instruments that have knife-edges to de-

ﬁne the exact points of contact. They can be used over

a wide range of gage lengths (10–2500 mm) and can be

modiﬁed to operate over a wide range of temperatures,

−75 to 1205

◦

C[7.18].

The second type of extensometer uses strain gages

to measure the deformation. The strain gage is usually

mounted on a beam within the extensometer that de-

forms elastically as the tensile specimen is deformed.

The strain gage is a wire grid that changes its resis-

tance as the beam is deformed elastically. To detect the

Table 7.1 Standard quasistatic tests for elastic constants

Speciﬁcation

number

Speciﬁcation title

ASTM E 111-04

[7.15]

Standard Test Method

for Young’s Modulus,

Tangent Modulus, and Chord

Modulus

ASTM E 132-04

[7.16]

Standard Test Method for

Poisson’s Ratio at Room

Temperature

ASTM E 143-02

[7.17]

Standard Test Method for

Shear Modulus at Room

Temperature

strain, the gage is connected to a bridge that measures

the resistance of the gage. The signal from the bridge is

conditioned and ampliﬁed before going to a digital read

out device. Using strain-gage extensometers, the ampli-

ﬁcation of the original displacement can be as high as

10 000 to 1 [7.18]. Strain gage extensometers are also

light and are easily attached onto the gage sections with

knife-edge clips.

Strain gages may be attached directly to the gage

section of the test specimen, in which case the strain

measured over a nominal gage length rather than the

more precise length typical of extensometers. Since the

calibration of individual strain gages and the integrity of

their attachment are often deduced by measuring a ma-

terial with a known elastic modulus, strain gages cannot

be used to certify a measurement of elastic modulus.

For noncritical applications, however, they are often the

simplest approach to acquiring elastic properties and

usually provide satisfactory results.

In ASTM E83[7.19], strain extensometers are clas-

siﬁed into six classes according to their accuracy. Only

the three most accurate classes, class A, class B1 and

sometimes class B2, can be used for evaluation of the

Young’s modulus of materials. To evaluate the perfor-

mance of a strain extensometer, veriﬁcation procedures

have been put forth by various standards organiza-

tions [7.18]. Class A extensometers show the highest

accuracy for strain measurements, but are generally not

available commercially [7.18]. Class B1 extensometers

are available commercially and are the ones most com-

monly used for elastic constant measurement. Class B2

can also be used for elastic constant determination on

plastics, which are high-compliance materials.

Test Procedures

Quasistatic tests to evaluate the elastic constants should

be carried out according to the procedures outlined in

the standard shown in Table 7.1.

These tests vary according to the materials tested

and the constant being determined. For metals the

Young’s modulus is determined by applying a tensile

load to the specimen following the procedure given in

ASTM E 111. The specimen is loaded uniaxially and

strain is obtained as a function of load. Stress is cal-

culated from the load; the linear portion of a plot of

stress versus strain is used to determine the Young’s

modulus. The linear section of the plot is ﬁtted by the

method of least squares and the Young’s modulus is

given by the slope of the plot. The coefﬁcient of de-

termination r

and the coefﬁcient of variation V

are

reported to give a measure of the goodness of the ﬁt.

Part C 7.1

Mechanical Properties 7.1 Elasticity 347

The test can be carried out either with calibrated dead

weights or, more often, by using a universal test ma-

chine. Class B1 extensometers are speciﬁed for the

test, and an averaging extensometer, or the average

of at least two extensometers arranged at equal an-

gles around the test specimen are recommended. The

standard points out that for many materials, Young’s

modulus determined in tension and compression are

not the same, so that separate determinations for each

mode of loading are recommended. Finally, the standard

notes that some materials loaded in the elastic range

exhibit some curvature and so should not be ﬁtted by

a straight line. For these materials, a tangent modu-

lus or a chord modulus are recommended for practical

applications.

The determination of Poisson’s ratio at room tem-

perature is described in ASTM E 132. Tests are carried

out on a universal test machine using the same sort of

specimens described in ASTM E 111. Average longi-

tudinal and transverse strains ε

and ε

are measured as

a function of applied load P. Two plots of strain versus

load are obtained. The data are ﬁtted to a linear equa-

tion by the method of least squares and the slopes of the

data are determined. Poisson’s ratio ν is calculated from

the ratio of the two slopes

ν =−(dε

/dP)/(dε

/dP) . (7.10)

As with the standard for determining Young’s modulus,

class B1 extensometers are speciﬁed for this test.

The determination of Young’s modulus and Pois-

son’s ratio on polymeric materials differs somewhat

from the same tests carried out on metals. Because

the Young’s modulus of polymers is only one hun-

dredth that of metals, strains are much higher than

those for metals. Hence, class B2 extensometers are

adequate for the determination of elastic constants of

polymers. Also, because of the high degree of sen-

sitivity of many plastics to the rate of straining and

to environment conditions these parameters must be

controlled and speciﬁed for each test. Furthermore,

according to statements in ASTM D 638 [7.21], the

standard test method for tensile properties of plastics,

data obtained by this test method cannot be consid-

ered valid for applications involving load time scales

or environments widely different from those of this test

method. In ASTM D 638, tests are carried out on

dumbbell-shaped specimens or on tubes speciﬁed. The

test speeds and the test conditions are speciﬁed and

the specimen is loaded in a universal test machine.

For polymers that exhibit an elastic region of behav-

ior, calculations for determining Young’s modulus and

Poisson’s ratio are the same as for metals. In case the

material exhibits no elastic behavior, a secant modulus

is suggested to approximate the elastic behavior of the

polymer.

Polymeric sheets are tested in tension according to

the procedures given in ASTM D 882 [7.22]. The mod-

ulus of elasticity determined by this test is an index

of stiffness of the plastic sheet. Specimens are sheets

of polymers at least 5 mm wide, but no greater than

25.4 mm wide. A length of 250 mm is considered stan-

dard. Because of the sensitivity of polymeric sheets

to environment, the sheets have to be conditioned to

the laboratory test environment prior to testing. Strain

rates are speciﬁed within the test procedure. The elas-

tic modulus is determined from the linear portion of

the stress–strain curve, or where the curve is nonlinear,

a secant modulus is determined as in ASTM D 638.

The Young’s moduli of ceramic materials, concretes

or stones are not determined in tension. Because of

the high value of the elastic constants and the weak-

ness of these materials in tension, the kinds of loads

needed for accurate strain measurements cannot be ap-

plied without rupture of these materials. The exception

to this statement is the testing of high-strength glass or

ceramic ﬁbers, which tend to be very strong and so,

can be subjected to sufﬁciently high loads for accu-

rate measurement of displacements. The tensile strength

and Young’s modulus of the ﬁber are calculated from

load-elongation and cross-sectional-area measurements

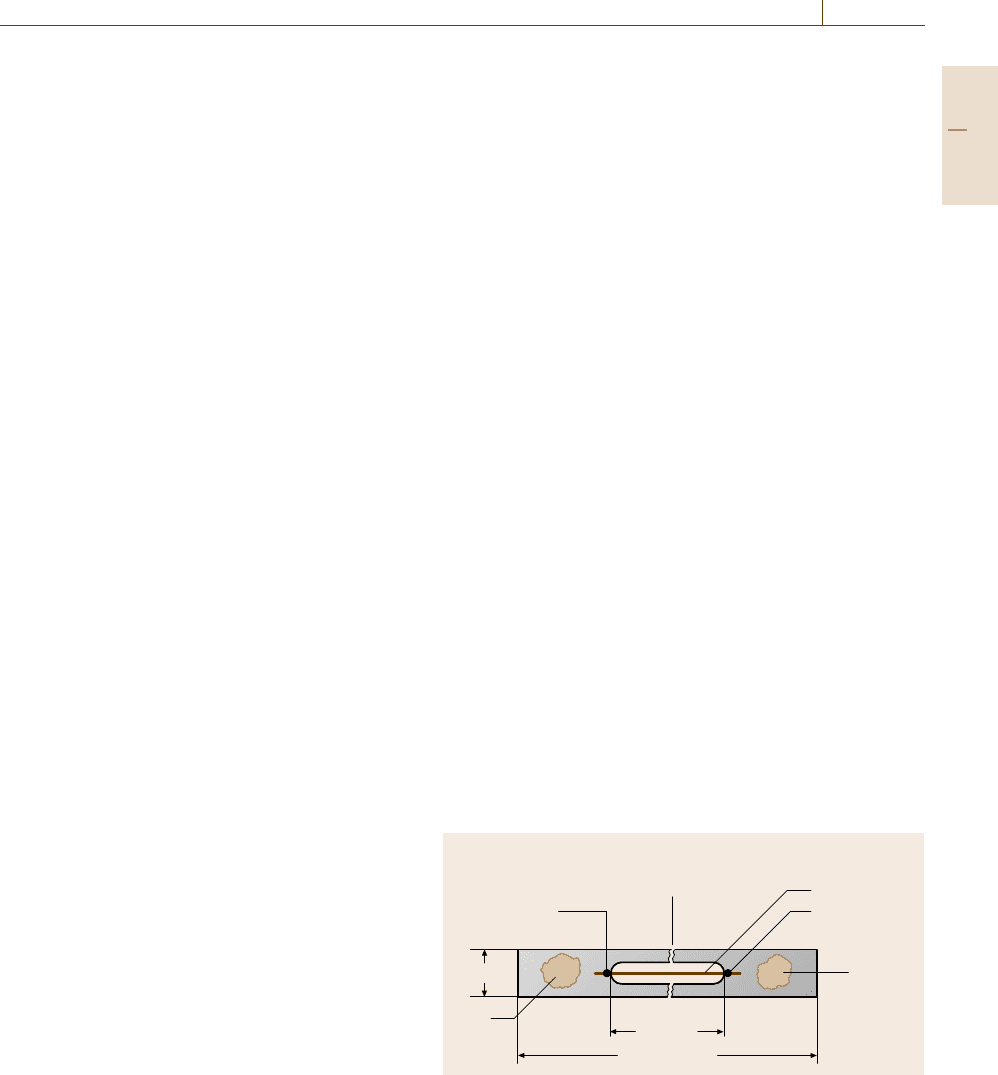
on the ﬁber. ASTM D 3379-75 [7.20] gives a proce-

dure that can be followed to test ceramic ﬁbers. Fibers

are glued onto a mounting tab that is gripped by the

test machine (Fig. 7.5). As shown in the ﬁgure, the gage

length is set by the tab. After the specimen has been

This section burned or cut

away after gripping in

test machine

Cement or wax

Test specimen

Width

Grip

area

Grip area

Gage

length

Overall length

Fig. 7.5 Method of mounting high-strength ceramic ﬁbers onto

a universal testing machine. The ﬁbers are glued onto a mounting

tab that is gripped by the test machine. After the specimen has been

mounted in the test machine, a section of the tab is cut or burned

away, leaving the specimen free to be tested (after [7.20])

Part C 7.1