Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


190 Г л а в а 7. Последовательности
11. Доажите, что для любоо четноо числа членов еомет-
ричесой прорессии S
неч
— сумма членов, стоящих на нечет-
ных местах, и S
чет
— сумма членов, стоящих на четных мес-
тах, связаны равенством qS
неч
= S
чет
.
12. Найдите первый и пятый члены еометричесой про-
рессии, если известно, что ее знаменатель равен 3, а сумма
шести первых членов равно 1820.
13. Найдите четыре последовательных члена возрастающей
еометричесой прорессии, если известно, что сумма райних
членов равна (–49), а сумма средних членов равна 14.
14. В еометричесой прорессии с положительными члена-
ми известно, что S
2
= 4, S
3
= 13. Найдите S
4
.
15. Сумма трех первых членов еометричесой прорессии
равна 13, а их произведение равно 27. Найдите эти числа.
16. Сумма трех первых членов еометричесой прорессии
равна 13, а сумма вадратов тех же чисел равна 91. Найдите
эти числа.
17. Определите три числа, являющиеся тремя последова-
тельными членами еометричесой прорессии, если их сумма
равна 21, а сумма обратных величин равна .
18. Сумма четырех первых членов еометричесой прорес-
сии равна 30, а сумма их вадратов равна 340. Найдите данные
числа.
19. Произведение трех первых членов еометричесой про-
рессии равно 64, а сумма убов этих членов равна 584. Найди-
те прорессию.
10. Сумма трех первых членов еометричесой прорессии
равна 31, а сумма первоо и третьео членов равна 26. Найдите
прорессию.
11. Число членов еометричесой прорессии четно. Сумма
всех ее членов в 3 раза больше суммы членов, стоящих на не-
четных местах. Определите знаменатель прорессии.
12. Дана еометричесая прорессия с положительными
членами. Выразите произведение n первых ее членов через их
сумму S
n
и через — сумму обратных величин этих членов.
13. Сумма любых пяти последовательных членов возрас-
тающей еометричесой прорессии в 19 раз больше третьео
из них. Найдите эту прорессию, если известно, что ее m-й член
равен единице.
7
12
------
S
n
′
§ 39. Геометрическая прогрессия 191
14. Вычислите сумму вадратов n членов еометричесой
прорессии, у оторой первый член равен u
1
и знаменатель q − 1.
15. Доажите, что отношение суммы вадратов нечетноо
числа членов еометричесой прорессии сумме первых сте-
пеней тех же членов является неоторым мноочленом относи-
тельно q (q— знаменатель прорессии).
16. Доажите, что если S
n
, S
2n
, S
3n
— суммы n, 2n, 3n пер-
вых членов еометричесой прорессии, то
S
n
(S
3n
– S
2n
) =
Найдите сумму:
17. x + + x
2
+ + ... + x
n
+ , x − ä1.
18. S
n
= + + + + ... +
19. S
n
= x + 2x
2
+ 3x
3
+ ... + nx
n
, x − 1.
20. Найдите число членов еометричесой прорессии, у о-
торой отношение суммы последних 14 членов сумме первых
14 членов равно 9, а отношение суммы всех членов без пер-
вых семи сумме всех членов без последних семи равно 3.
П р и м е р 2. Найти отличный от нуля знаменатель бесо-
нечно убывающей еометричесой прорессии, у оторой аж-
дый член в 4 раза больше суммы всех ее последующих членов.
(Считается, что b
1
− 0.)
Р е ш е н и е. Составим уравнение, связывающее n-й член
прорессии с суммой ее членов, начиная с (n + 1)-о:
b
n
= 4 .
Выразив b
n
и b
n + 1
через b
1
и q, получаем уравнение
b
1
q
n – 1
= 4 ,
оторое после деления обеих ео частей на b
1
q
n – 1
примет вид
1 = . Ео орнем является q = 0,2.
Ответ. q = 0,2.
(S
2n
S
n
)
2
.–
1
x
---
2
1
x
2
------
2
1
x
n
------
2
1
2
0
------
2
2
1
------
3
2
2
------
4
2
3
------
n
2
n
1–
---------------- .
b
n 1+
1 q–
------------- -
b
1
q
n
1 q–
------------ -
4q
1 q–
------------ -

190 Г л а в а 7. Последовательности
11. Доажите, что для любоо четноо числа членов еомет-
ричесой прорессии S
неч
— сумма членов, стоящих на нечет-
ных местах, и S
чет
— сумма членов, стоящих на четных мес-
тах, связаны равенством qS
неч
= S
чет
.
12. Найдите первый и пятый члены еометричесой про-
рессии, если известно, что ее знаменатель равен 3, а сумма
шести первых членов равно 1820.
13. Найдите четыре последовательных члена возрастающей
еометричесой прорессии, если известно, что сумма райних
членов равна (–49), а сумма средних членов равна 14.
14. В еометричесой прорессии с положительными члена-
ми известно, что S
2
= 4, S
3
= 13. Найдите S
4
.
15. Сумма трех первых членов еометричесой прорессии
равна 13, а их произведение равно 27. Найдите эти числа.
16. Сумма трех первых членов еометричесой прорессии
равна 13, а сумма вадратов тех же чисел равна 91. Найдите
эти числа.
17. Определите три числа, являющиеся тремя последова-
тельными членами еометричесой прорессии, если их сумма
равна 21, а сумма обратных величин равна .
18. Сумма четырех первых членов еометричесой прорес-
сии равна 30, а сумма их вадратов равна 340. Найдите данные
числа.
19. Произведение трех первых членов еометричесой про-
рессии равно 64, а сумма убов этих членов равна 584. Найди-
те прорессию.
10. Сумма трех первых членов еометричесой прорессии
равна 31, а сумма первоо и третьео членов равна 26. Найдите
прорессию.
11. Число членов еометричесой прорессии четно. Сумма
всех ее членов в 3 раза больше суммы членов, стоящих на не-
четных местах. Определите знаменатель прорессии.
12. Дана еометричесая прорессия с положительными
членами. Выразите произведение n первых ее членов через их
сумму S
n
и через — сумму обратных величин этих членов.
13. Сумма любых пяти последовательных членов возрас-
тающей еометричесой прорессии в 19 раз больше третьео
из них. Найдите эту прорессию, если известно, что ее m-й член
равен единице.
7
12
------
S
n
′
§ 39. Геометрическая прогрессия 191
14. Вычислите сумму вадратов n членов еометричесой
прорессии, у оторой первый член равен u
1
и знаменатель q − 1.
15. Доажите, что отношение суммы вадратов нечетноо
числа членов еометричесой прорессии сумме первых сте-
пеней тех же членов является неоторым мноочленом относи-
тельно q (q— знаменатель прорессии).
16. Доажите, что если S
n
, S
2n
, S
3n
— суммы n, 2n, 3n пер-
вых членов еометричесой прорессии, то
S
n
(S
3n
– S
2n
) =
Найдите сумму:
17. x + + x
2
+ + ... + x
n
+ , x − ä1.
18. S
n
= + + + + ... +
19. S
n
= x + 2x
2
+ 3x
3
+ ... + nx
n
, x − 1.
20. Найдите число членов еометричесой прорессии, у о-
торой отношение суммы последних 14 членов сумме первых
14 членов равно 9, а отношение суммы всех членов без пер-
вых семи сумме всех членов без последних семи равно 3.
П р и м е р 2. Найти отличный от нуля знаменатель бесо-
нечно убывающей еометричесой прорессии, у оторой аж-
дый член в 4 раза больше суммы всех ее последующих членов.
(Считается, что b
1
− 0.)
Р е ш е н и е. Составим уравнение, связывающее n-й член
прорессии с суммой ее членов, начиная с (n + 1)-о:
b
n
= 4 .
Выразив b
n
и b
n + 1
через b
1
и q, получаем уравнение
b
1
q
n – 1
= 4 ,
оторое после деления обеих ео частей на b
1
q
n – 1
примет вид
1 = . Ео орнем является q = 0,2.
Ответ. q = 0,2.
(S
2n
S
n
)
2
.–
1
x
---
2
1
x
2
------
2
1
x
n
------
2
1
2
0
------
2
2
1
------
3
2
2
------
4
2
3
------
n
2
n
1–
---------------- .
b
n 1+
1 q–
------------- -
b
1
q
n
1 q–
------------ -
4q
1 q–
------------ -

192 Г л а в а 7. Последовательности
21. Сумма бесонечно убывающей еометричесой прорес-
сии равна 16, а сумма вадратов ее членов равна 153 . Найди-
те четвертый член и знаменатель прорессии.
22. Найдите знаменатель бесонечно убывающей еометри-
чесой прорессии, у оторой отношение аждоо члена сум-
ме всех последующих членов равно .
23. В бесонечно убывающей еометричесой прорессии
с положительными членами сумма трех первых членов равна
10,5, а сумма прорессии равна 12. Найдите прорессию.
24. Сумма бесонечно убывающей еометричесой прорес-
сии равна 4, а сумма убов ее членов равна 192. Найдите пер-
вый член и знаменатель прорессии.
25. Первый член неоторой бесонечно убывающей еомет-
ричесой прорессии равен единице, а сумма прорессии рав-
на S. Найдите сумму вадратов членов прорессии.
26. При аом значении x прорессия
, , ,...,де a > 0,
является бесонечно убывающей? Найдите сумму этой про-
рессии.
27. Сторона вадрата равна a. Середины сторон этоо вад-
рата соединили отрезами и получили новый вадрат. С этим
вадратом поступили та же, а с исходным, и т. д. Найдите
предел P суммы периметров и предел S суммы площадей этих
вадратов.
28. Найдите условие, при отором три числа a, b и c были
бы соответственно k-м, p-м и m-м членами еометричесой про-
рессии.
29. Моут ли числа 11, 12, 13 быть членами (не обязательно
соседними) одной еометричесой прорессии?
30. Бесонечно убывающая еометричесая прорессия, сум-
ма оторой равна , содержит член . Отношение суммы всех
членов, предшествующих ему, сумме всех членов, следую-
щих за ним, равно 30. Определите порядовый номер этоо
члена.
31. Найдите отношение первоо члена бесонечно убываю-
щей еометричесой прорессии сумме всех ее членов, если
3
5
---
2
3
---
ax+
ax–
------------- -
ax–
ax+
------------- -
ax–
ax+
------------- -
3
16
3
------
1
6
---
§ 40. Смешанные задачи на прогрессии 193
отношение всех членов этой прорессии, имеющих четные
номера, сумме всех членов, номера оторых ратны трем,
равно 3.
§ 40. Смешанные задачи на прогрессии
Смешанными задачами на прорессию принято называть та-
ие задачи, при решении оторых используются свойства а
арифметичесой, та и еометричесой прорессий.
П р и м е р. Три числа являются последовательными члена-
ми еометричесой прорессии. Если от третьео отнять 4, то
эти числа оажутся последовательными членами арифметиче-
сой прорессии. Если же от второо и третьео членов этой
арифметичесой прорессии отнять по 1, то полученные числа
снова оажутся последовательными членами еометричесой
прорессии. Найти эти числа.
Р е ш е н и е. Обозначим исомые числа через a, b, c. Для
составления первоо уравнения, связывающео a, b и c, исполь-
зуем свойство членов еометричесой прорессии:
b
2
= ac.
Из условия задачи и свойства членов арифметичесой прорес-
сии получим второе уравнение
2b = a + c – 4.
Наонец, последнее условие задачи можно записать в виде
уравнения
(b – 1)
2
= a(c – 5).
Чтобы решить систему
(*)
вычтем из первоо уравнения третье. Тода получим линейное
уравнение 2b – 1 = 5a, связывающее b и a. Выразив теперь из
системы линейных уравнений
b
2
= ac,
2b = a + c – 4,
(b – 1)
2
= a(c – 5),
2b – 1 = 5a,
2b = a + c – 4

192 Г л а в а 7. Последовательности
21. Сумма бесонечно убывающей еометричесой прорес-
сии равна 16, а сумма вадратов ее членов равна 153 . Найди-
те четвертый член и знаменатель прорессии.
22. Найдите знаменатель бесонечно убывающей еометри-
чесой прорессии, у оторой отношение аждоо члена сум-
ме всех последующих членов равно .
23. В бесонечно убывающей еометричесой прорессии
с положительными членами сумма трех первых членов равна
10,5, а сумма прорессии равна 12. Найдите прорессию.
24. Сумма бесонечно убывающей еометричесой прорес-
сии равна 4, а сумма убов ее членов равна 192. Найдите пер-
вый член и знаменатель прорессии.
25. Первый член неоторой бесонечно убывающей еомет-
ричесой прорессии равен единице, а сумма прорессии рав-
на S. Найдите сумму вадратов членов прорессии.
26. При аом значении x прорессия
, , ,...,де a > 0,
является бесонечно убывающей? Найдите сумму этой про-
рессии.
27. Сторона вадрата равна a. Середины сторон этоо вад-
рата соединили отрезами и получили новый вадрат. С этим
вадратом поступили та же, а с исходным, и т. д. Найдите
предел P суммы периметров и предел S суммы площадей этих
вадратов.
28. Найдите условие, при отором три числа a, b и c были
бы соответственно k-м, p-м и m-м членами еометричесой про-
рессии.
29. Моут ли числа 11, 12, 13 быть членами (не обязательно
соседними) одной еометричесой прорессии?
30. Бесонечно убывающая еометричесая прорессия, сум-
ма оторой равна , содержит член . Отношение суммы всех
членов, предшествующих ему, сумме всех членов, следую-
щих за ним, равно 30. Определите порядовый номер этоо
члена.
31. Найдите отношение первоо члена бесонечно убываю-
щей еометричесой прорессии сумме всех ее членов, если
3
5
---
2
3
---
ax+
ax–
------------- -
ax–
ax+
------------- -
ax–
ax+
------------- -
3
16
3
------
1
6
---
§ 40. Смешанные задачи на прогрессии 193
отношение всех членов этой прорессии, имеющих четные
номера, сумме всех членов, номера оторых ратны трем,
равно 3.
§ 40. Смешанные задачи на прогрессии
Смешанными задачами на прорессию принято называть та-
ие задачи, при решении оторых используются свойства а
арифметичесой, та и еометричесой прорессий.
П р и м е р. Три числа являются последовательными члена-
ми еометричесой прорессии. Если от третьео отнять 4, то
эти числа оажутся последовательными членами арифметиче-
сой прорессии. Если же от второо и третьео членов этой
арифметичесой прорессии отнять по 1, то полученные числа
снова оажутся последовательными членами еометричесой
прорессии. Найти эти числа.
Р е ш е н и е. Обозначим исомые числа через a, b, c. Для
составления первоо уравнения, связывающео a, b и c, исполь-
зуем свойство членов еометричесой прорессии:
b
2
= ac.
Из условия задачи и свойства членов арифметичесой прорес-
сии получим второе уравнение
2b = a + c – 4.
Наонец, последнее условие задачи можно записать в виде
уравнения
(b – 1)
2
= a(c – 5).
Чтобы решить систему
(*)
вычтем из первоо уравнения третье. Тода получим линейное
уравнение 2b – 1 = 5a, связывающее b и a. Выразив теперь из
системы линейных уравнений
b
2
= ac,
2b = a + c – 4,
(b – 1)
2
= a(c – 5),
2b – 1 = 5a,
2b = a + c – 4

194 Г л а в а 7. Последовательности
неизвестные a и c через b, имеем
a = , c = . (**)
Теперь подставим выражения (**) в первое уравнение систе-
мы (*). Тода получим вадратное уравнение
9b
2
– 34b + 21 = 0,
орни отороо равны 3 и . Подставив эти значения b в выра-
жения (**), находим исомые числа.
Ответ.1; 3; 9 или ; ; .
1. Три числа являются последовательными членами еомет-
ричесой прорессии. Если увеличить второе число на 2, то эти
три числа станут членами арифметичесой прорессии, а если
затем увеличить последнее число на 9, то вновь полученные
числа опять оажутся членами еометричесой прорессии.
Найдите исходные числа.
2. Три числа, из оторых третье равно 12, являются тремя
последовательными членами еометричесой прорессии. Если
вместо 12 взять 9, то эти три числа станут тремя последова-
тельными членами арифметичесой прорессии. Найдите ис-
ходные числа.
3. Дано трехзначное число, цифры отороо являются тремя
последовательными членами еометричесой прорессии. Если
из этоо числа вычесть 792, то получится число, записанное
теми же цифрами, но в обратном поряде. Если же из цифры
исходноо числа, обозначающей число сотен, вычесть 4, а ос-
тальные цифры оставить без изменения, то получится число,
цифры отороо являются последовательными членами ариф-
метичесой прорессии. Найдите исходное число.
4. Даны четыре числа, из оторых первые три являются тре-
мя последовательными членами еометричесой, а последние
три — членами арифметичесой прорессии; сумма райних чи-
сел равна 32, сумма средних чисел равна 24. Найдите эти числа.
5. Первые члены арифметичесой и еометричесой про-
рессий одинаовы и равны 2, третьи члены таже одинаовы,
а вторые отличаются на 4. Найдите эти прорессии, если все их
члены положительны.
6. Первый член арифметичесой прорессии равен 1, а сум-
ма девяти первых членов равна 369. Первый и девятый члены
еометричесой прорессии совпадают с первым и девятым чле-
2b 1–
5
---------------- -
8b 21+
5
-------------------- -
7
9
---
1
9
---
7
9
---
49
9
------
§ 41. Разные задачи 195
нами арифметичесой прорессии. Найдите седьмой член еомет-
ричесой прорессии.
17. Среди 11 членов арифметичесой прорессии первый,
пятый и одиннадцатый являются тремя последовательными
членами неоторой еометричесой прорессии. Найдите ариф-
метичесую прорессию, если ее первый член равен 24.
18. В неоторой арифметичесой прорессии второй член
является средним пропорциональным между первым и четвер-
тым. Поажите, что четвертый, шестой и девятый члены этой
прорессии являются последовательными членами еометриче-
сой прорессии. Найдите знаменатель этой прорессии.
19. Доажите, что если a, b и c одновременно являются 5-м,
17-м и 37-м членами а арифметичесой, та и еометриче-
сой прорессии, то a
b – c
b
c – a
c
a – b
= 1.
10. Доажите, что если a, b, c— три последовательных чле-
на еометричесой прорессии, то , , — по-
следовательные члены арифметичесой прорессии. (Считает-
ся, что числа a, b, c положительны и не равны единице.)
11. Даны две прорессии: еометричесая с общим членом
b
n
> 0 и знаменателем q и возрастающая арифметичесая с об-
щим членом a
n
и разностью d. Найдите x из условия log
x
b
n
– a
n
=
= log
x
b
1
– a
1
.
§ 41. Разные задачи
Установите, ораничена ли последовательность:
1. x
n
= 1 + . 2. x
n
= n(1 – ). 3. x
n
= .
4. Общий член последовательности представлен в виде
x
n
= + + ... +
Сольо членов последовательности меньше ?
5. Доажите, что последовательность
u
1
= 3, u
n + 1
=
является убывающей.
1
log
a
N
-----------------
1
log
b
N
-----------------
1
log
c
N
-----------------
(–1)
n
1
n
---
(–1)
n
3n 5+
2n 3–
------------------
1
2
---
1
4
---
1
2
n
------ .
1023
1024
-------------
2 u
n
2
+
2u
n
-----------------

194 Г л а в а 7. Последовательности
неизвестные a и c через b, имеем
a = , c = . (**)
Теперь подставим выражения (**) в первое уравнение систе-
мы (*). Тода получим вадратное уравнение
9b
2
– 34b + 21 = 0,
орни отороо равны 3 и . Подставив эти значения b в выра-
жения (**), находим исомые числа.
Ответ.1; 3; 9 или ; ; .
1. Три числа являются последовательными членами еомет-
ричесой прорессии. Если увеличить второе число на 2, то эти
три числа станут членами арифметичесой прорессии, а если
затем увеличить последнее число на 9, то вновь полученные
числа опять оажутся членами еометричесой прорессии.
Найдите исходные числа.
2. Три числа, из оторых третье равно 12, являются тремя
последовательными членами еометричесой прорессии. Если
вместо 12 взять 9, то эти три числа станут тремя последова-
тельными членами арифметичесой прорессии. Найдите ис-
ходные числа.
3. Дано трехзначное число, цифры отороо являются тремя
последовательными членами еометричесой прорессии. Если
из этоо числа вычесть 792, то получится число, записанное
теми же цифрами, но в обратном поряде. Если же из цифры
исходноо числа, обозначающей число сотен, вычесть 4, а ос-
тальные цифры оставить без изменения, то получится число,
цифры отороо являются последовательными членами ариф-
метичесой прорессии. Найдите исходное число.
4. Даны четыре числа, из оторых первые три являются тре-
мя последовательными членами еометричесой, а последние
три — членами арифметичесой прорессии; сумма райних чи-
сел равна 32, сумма средних чисел равна 24. Найдите эти числа.
5. Первые члены арифметичесой и еометричесой про-
рессий одинаовы и равны 2, третьи члены таже одинаовы,
а вторые отличаются на 4. Найдите эти прорессии, если все их
члены положительны.
6. Первый член арифметичесой прорессии равен 1, а сум-
ма девяти первых членов равна 369. Первый и девятый члены
еометричесой прорессии совпадают с первым и девятым чле-
2b 1–
5
---------------- -
8b 21+
5
-------------------- -
7
9
---
1
9
---
7
9
---
49
9
------
§ 41. Разные задачи 195
нами арифметичесой прорессии. Найдите седьмой член еомет-
ричесой прорессии.
17. Среди 11 членов арифметичесой прорессии первый,
пятый и одиннадцатый являются тремя последовательными
членами неоторой еометричесой прорессии. Найдите ариф-
метичесую прорессию, если ее первый член равен 24.
18. В неоторой арифметичесой прорессии второй член
является средним пропорциональным между первым и четвер-
тым. Поажите, что четвертый, шестой и девятый члены этой
прорессии являются последовательными членами еометриче-
сой прорессии. Найдите знаменатель этой прорессии.
19. Доажите, что если a, b и c одновременно являются 5-м,
17-м и 37-м членами а арифметичесой, та и еометриче-
сой прорессии, то a
b – c
b
c – a
c
a – b
= 1.
10. Доажите, что если a, b, c— три последовательных чле-
на еометричесой прорессии, то , , — по-
следовательные члены арифметичесой прорессии. (Считает-
ся, что числа a, b, c положительны и не равны единице.)
11. Даны две прорессии: еометричесая с общим членом
b
n
> 0 и знаменателем q и возрастающая арифметичесая с об-
щим членом a
n
и разностью d. Найдите x из условия log
x
b
n
– a
n
=
= log
x
b
1
– a
1
.
§ 41. Разные задачи
Установите, ораничена ли последовательность:
1. x
n
= 1 + . 2. x
n
= n(1 – ). 3. x
n
= .
4. Общий член последовательности представлен в виде
x
n
= + + ... +
Сольо членов последовательности меньше ?
5. Доажите, что последовательность
u
1
= 3, u
n + 1
=
является убывающей.
1
log
a
N
-----------------
1
log
b
N
-----------------
1
log
c
N
-----------------
(–1)
n
1
n
---
(–1)
n
3n 5+
2n 3–
------------------
1
2
---
1
4
---
1
2
n
------ .
1023
1024
-------------
2 u
n
2
+
2u
n
-----------------
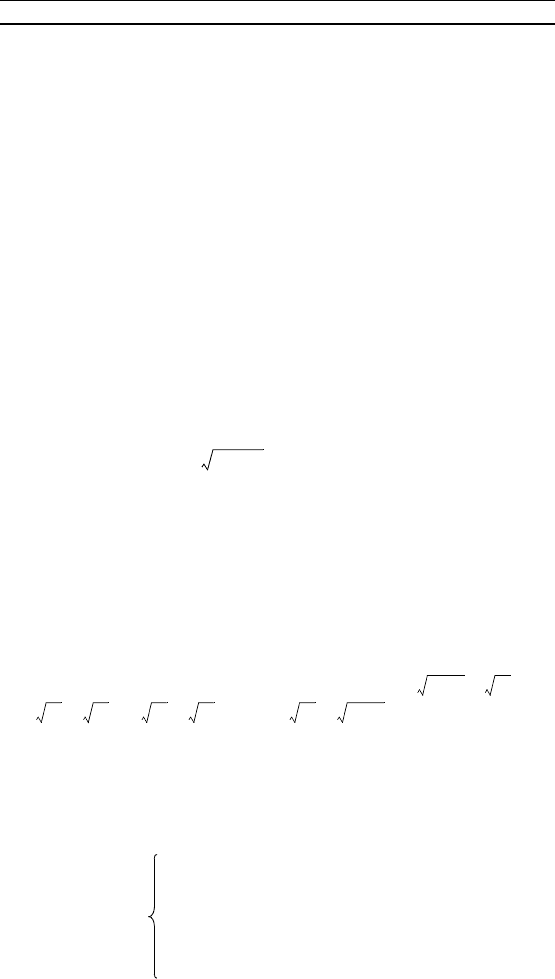
196 Г л а в а 7. Последовательности
6. Доажите, что последовательность
u
n
= 1 + + + ... + ,
является возрастающей.
7. Пусть a
n
— сторона правильноо уольниа, впи-
санноо в оружность радиуса 1. Доажите, что последователь-
ность (a
n
) является убывающей, а последовательность перимет-
ров (P
n
) — возрастающей.
18. Катет равнобедренноо прямоуольноо треуольниа
разделен на n равных частей, и на полученных отрезах постро-
ены вписанные прямоуольнии. Найдите предел последова-
тельности (S
n
) площадей, образованных из ступенчатых фиур.
19. Найдите площадь фиуры, ораниченной параболой y = x
2
,
отрезом [0; 1] оси абсцисс и прямой x = 1, а предел последо-
вательности площадей ступенчатых фиур, состоящих из пря-
моуольниов, построенных та же, а в предыдущей задаче.
10. Найдите ( – n).
11. Найдите трехзначное число, оторое делится на 45 и циф-
ры отороо являются последовательными членами арифмети-
чесой прорессии.
12. Доажите, что если в арифметичесой прорессии S
n
= n
2
p,
S
k
= k
2
p, k − n, то S
p
= p
3
.
13. Доажите, что если a
1
, a
2
, ..., a
n
— члены арифметиче-
сой прорессии с разностью d, то
+ + ... + = .
14. Четыре числа a, b, c, d являются членами еометриче-
сой прорессии. Доажите, что
(a – c)
2
+ (b – c)
2
+ (b – d)
2
= (a – d)
2
.
15. Решите систему уравнений
1
2
---
1
2
2
------
1
2
n
------
2
n 1+
-
n º×
lim n
3
1+
3
1
a
1
a
2
+
--------------------------- -
1
a
2
a
3
+
--------------------------- -
1
a
n
a
n 1+
+
------------------------------------
a
n 1+
a
1
–
d
-----------------------------------
= = = = ,
x = 8u,
x + y + z + u + s + t = 15 .
x
y
---
y
z
---
z
u
---
u
s
---
s
t
--
3
4
---
§ 41. Разные задачи 197
16. Доажите равенство
+ = .
17. Пусть x
1
и x
2
— орни уравнения x
2
– 3x + A = 0, а x
3
и
x
4
— орни уравнения x
2
– 12x + B = 0. Известно, что последо-
вательность x
1
, x
2
, x
3
, x
4
является возрастающей еометриче-
сой прорессией. Найдите A и B.
В неоторых случаях сумму n членов произвольной после-
довательности можно найти с помощью построения вспомоа-
тельной последовательности {S
n
}, удовлетворяющей условию
S
k + 1
– S
k
= u
k
.(1)
Нетрудно убедиться, что
u
1
+ u
2
+ ... + u
n
=
= (S
2
– S
1
) + (S
3
– S
2
) + ... + (S
n + 1
– S
n
) = S
n + 1
– S
1
.(2)
П р и м е р. Найти сумму
+ + ... + ,
если известно, что a
1
, a
2
, ..., a
n + 1
— последовательные члены
арифметичесой прорессии с разностью d − 0, ни один из о-
торых не равен нулю.
Р е ш е н и е. Записав дробь в виде
= – · = – ,
де d = a
2
– a
1
, и взяв S
k
равным
S
k
= – ,
имеем
S
k + 1
– S
k
= – – = = = u
k
.
(66...6)
2
n цифр
88...8
n цифр
44...4
2n цифр
1
a
1
a
2
-------------
1
a
2
a
3
-------------
1
a
n
a
n 1+
---------------------
1
a
1
a
2
-------------
1
a
1
a
2
-------------
1
a
1
----- -
1
a
2
----- -
1
a
2
a
1
–
------------------ -
1
a
1
----- -
1
a
2
----- -
1
d
---
1
d
---
1
a
k
----- -
1
d
---
1
a
k 1+
------------- -
1
a
k
----- -
1
d
---
a
k 1+
a
k
–
a
k 1+
a
k
-------------------------- -
1
a
k 1+
a
k
--------------------
196 Г л а в а 7. Последовательности
6. Доажите, что последовательность
u
n
= 1 + + + ... + ,
является возрастающей.
7. Пусть a
n
— сторона правильноо уольниа, впи-
санноо в оружность радиуса 1. Доажите, что последователь-
ность (a
n
) является убывающей, а последовательность перимет-
ров (P
n
) — возрастающей.
18. Катет равнобедренноо прямоуольноо треуольниа
разделен на n равных частей, и на полученных отрезах постро-
ены вписанные прямоуольнии. Найдите предел последова-
тельности (S
n
) площадей, образованных из ступенчатых фиур.
19. Найдите площадь фиуры, ораниченной параболой y = x
2
,
отрезом [0; 1] оси абсцисс и прямой x = 1, а предел последо-
вательности площадей ступенчатых фиур, состоящих из пря-
моуольниов, построенных та же, а в предыдущей задаче.
10. Найдите ( – n).
11. Найдите трехзначное число, оторое делится на 45 и циф-
ры отороо являются последовательными членами арифмети-
чесой прорессии.
12. Доажите, что если в арифметичесой прорессии S
n
= n
2
p,
S
k
= k
2
p, k − n, то S
p
= p
3
.
13. Доажите, что если a
1
, a
2
, ..., a
n
— члены арифметиче-
сой прорессии с разностью d, то
+ + ... + = .
14. Четыре числа a, b, c, d являются членами еометриче-
сой прорессии. Доажите, что
(a – c)
2
+ (b – c)
2
+ (b – d)
2
= (a – d)
2
.
15. Решите систему уравнений
1
2
---
1
2
2
------
1
2
n
------
2
n 1+
-
n º×
lim n
3
1+
3
1
a
1
a
2
+
--------------------------- -
1
a
2
a
3
+
--------------------------- -
1
a
n
a
n 1+
+
------------------------------------
a
n 1+
a
1
–
d
-----------------------------------
= = = = ,
x = 8u,
x + y + z + u + s + t = 15 .
x
y
---
y
z
---
z
u
---
u
s
---
s
t
--
3
4
---
§ 41. Разные задачи 197
16. Доажите равенство
+ = .
17. Пусть x
1
и x
2
— орни уравнения x
2
– 3x + A = 0, а x
3
и
x
4
— орни уравнения x
2
– 12x + B = 0. Известно, что последо-
вательность x
1
, x
2
, x
3
, x
4
является возрастающей еометриче-
сой прорессией. Найдите A и B.
В неоторых случаях сумму n членов произвольной после-
довательности можно найти с помощью построения вспомоа-
тельной последовательности {S
n
}, удовлетворяющей условию
S
k + 1
– S
k
= u
k
.(1)
Нетрудно убедиться, что
u
1
+ u
2
+ ... + u
n
=
= (S
2
– S
1
) + (S
3
– S
2
) + ... + (S
n + 1
– S
n
) = S
n + 1
– S
1
.(2)
П р и м е р. Найти сумму
+ + ... + ,
если известно, что a
1
, a
2
, ..., a
n + 1
— последовательные члены
арифметичесой прорессии с разностью d − 0, ни один из о-
торых не равен нулю.
Р е ш е н и е. Записав дробь в виде
= – · = – ,
де d = a
2
– a
1
, и взяв S
k
равным
S
k
= – ,
имеем
S
k + 1
– S
k
= – – = = = u
k
.
(66...6)
2
n цифр
88...8
n цифр
44...4
2n цифр
1
a
1
a
2
-------------
1
a
2
a
3
-------------
1
a
n
a
n 1+
---------------------
1
a
1
a
2
-------------
1
a
1
a
2
-------------
1
a
1
----- -
1
a
2
----- -
1
a
2
a
1
–
------------------ -
1
a
1
----- -
1
a
2
----- -
1
d
---
1
d
---
1
a
k
----- -
1
d
---
1
a
k 1+
------------- -
1
a
k
----- -
1
d
---
a
k 1+
a
k
–
a
k 1+
a
k
-------------------------- -
1
a
k 1+
a
k
--------------------

198 Г л а в а 7. Последовательности
Далее, используя равенства (1) и (2), получаем
+ + ... + = S
n + 1
– S
1
=
= – – = .
Ответ..
Доажите тождество:
18. + + + ... + = 1 – .
19. + + + ... + =
= – .
20. + + ... + =
= .
21. Пусть a
1
, ..., a
n
— арифметичесая прорессия. Доа-
жите тождество
+ + ... + = + + ... + .
22. Найдите сумму n чисел вида 1, 11, 111, 1111, ... .
23. Найдите сумму:
а) 1 – 2 + 3 – 4 + ... + (–n);
б) 1
2
– 2
2
+ 3
2
– 4
2
+ ... + · n
2
;
в) 2 · 1
2
+ 3 · 2
2
+ ... + (n + 1)n
2
.
При вычислении пределов последовательностей, члены о-
торых являются результатами суммирования, используют сле-
дующие формулы:
1 + 2 + ... + n = , (3)
1
2
+ 2
2
+ ... + n
2
= , (4)
1
3
+ 2
3
+ ... + n
3
= . (5)
1
a
1
a
2
-------------
1
a
2
a
3
-------------
1
a
n
a
n 1+
---------------------
1
d
---
1
a
n 1+
--------------
1
a
1
----- -
n
a
n 1+
a
1
-------------------- -
n
a
n 1+
a
1
-------------------- -
1
12⋅
-----------
1
23⋅
-----------
1
34⋅
-----------
1
nn 1+()
-----------------------
1
n 1+
------------- -
1
123⋅⋅
-------------------
1
234⋅⋅
-------------------
1
345⋅⋅
-------------------
1
nn 1+()n 2+()
------------------------------------------ -
1
2
---
1
2
---
1
n 1+()n 2+()
---------------------------------------
1
135⋅⋅
-------------------
1
357⋅⋅
-------------------
n
2n 1–()2n 1+()2n 3+()
----------------------------------------------------------------------
nn 1+()
22n 1+()2n 3+()
--------------------------------------------------
1
a
1
a
n
------------ -
1
a
2
a
n 1–
--------------------
1
a
n
a
1
------------ -
2
a
1
a
n
------------ -
1
a
1
----- -
1
a
2
----- -
1
a
n
------
(–1)
n 1+
nn 1+()
2
-----------------------
nn 1+()2n 1+()
6
---------------------------------------------- -
n
2
n 1+()
2
4
---------------------------- -
§ 41. Разные задачи 199
Используя равенства (3)—(5) и формулы для сумм n чле-
нов арифметичесой и еометричесой прорессий, вычислите
предел:
24.
25. + + ... + .
26. + + + ... + .
27. – .
28. + + ... + + .
29. + + ... + .
30. + + ... + .
31. + + ... + , де (a
n
)— арифме-
тичесая прорессия с разностью d, члены оторой отличны
от нуля.
32. + + ... + .
Найдите предел последовательности:
33. a
n
= · ... (в последнем
сомножителе n радиалов).
34. a
n
= (n радиалов).
35. a
n
= (n радиалов).
n º×
lim
1 2 ... + 2
n
++
1 5 ... + 5
n
++
----------------------------------------- .
n º×
lim
1
n
2
------
2
n
2
------
n 1–
n
2
-------------
n º×
lim
3
1
3
-------
1
33
-----------
3
3
n 1–
------------- -
n º×
lim
1 3 5 ... 2n 1+()+++ +
n 1+
--------------------------------------------------------------------
2n 1–
2
-----------------
n º×
lim
1
2
n
3
------
2
2
n
3
------
n 1–()
2
n
3
---------------------
1
n
---
n º×
lim
7
10
------
29
10
2
---------
5
n
2
n
+
10
n
------------------- -
n º×
lim
1
12⋅
-----------
1
23⋅
-----------
1
nn 1+()
-----------------------
n º×
lim
1
a
1
a
2
-------------
1
a
2
a
3
-------------
1
a
n
a
n 1+
---------------------
n º×
lim
1
n
4
------
8
n
4
------
n
3
n
4
------
2
2
-------
2
22+
----------------------
2
2 2 ... 2 2++++
-----------------------------------------------------------------
aa... a+++
22...2++–
2 2 ... 3++–
------------------------------------------------- -
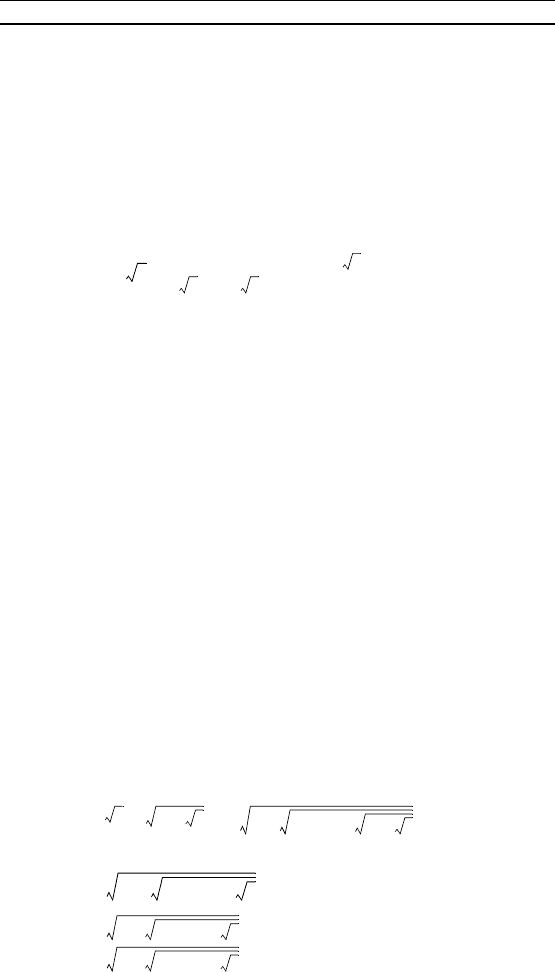
198 Г л а в а 7. Последовательности
Далее, используя равенства (1) и (2), получаем
+ + ... + = S
n + 1
– S
1
=
= – – = .
Ответ..
Доажите тождество:
18. + + + ... + = 1 – .
19. + + + ... + =
= – .
20. + + ... + =
= .
21. Пусть a
1
, ..., a
n
— арифметичесая прорессия. Доа-
жите тождество
+ + ... + = + + ... + .
22. Найдите сумму n чисел вида 1, 11, 111, 1111, ... .
23. Найдите сумму:
а) 1 – 2 + 3 – 4 + ... + (–n);
б) 1
2
– 2
2
+ 3
2
– 4
2
+ ... + · n
2
;
в) 2 · 1
2
+ 3 · 2
2
+ ... + (n + 1)n
2
.
При вычислении пределов последовательностей, члены о-
торых являются результатами суммирования, используют сле-
дующие формулы:
1 + 2 + ... + n = , (3)
1
2
+ 2
2
+ ... + n
2
= , (4)
1
3
+ 2
3
+ ... + n
3
= . (5)
1
a
1
a
2
-------------
1
a
2
a
3
-------------
1
a
n
a
n 1+
---------------------
1
d
---
1
a
n 1+
--------------
1
a
1
----- -
n
a
n 1+
a
1
-------------------- -
n
a
n 1+
a
1
-------------------- -
1
12⋅
-----------
1
23⋅
-----------
1
34⋅
-----------
1
nn 1+()
-----------------------
1
n 1+
------------- -
1
123⋅⋅
-------------------
1
234⋅⋅
-------------------
1
345⋅⋅
-------------------
1
nn 1+()n 2+()
------------------------------------------ -
1
2
---
1
2
---
1
n 1+()n 2+()
---------------------------------------
1
135⋅⋅
-------------------
1
357⋅⋅
-------------------
n
2n 1–()2n 1+()2n 3+()
----------------------------------------------------------------------
nn 1+()
22n 1+()2n 3+()
--------------------------------------------------
1
a
1
a
n
------------ -
1
a
2
a
n 1–
--------------------
1
a
n
a
1
------------ -
2
a
1
a
n
------------ -
1
a
1
----- -
1
a
2
----- -
1
a
n
------
(–1)
n 1+
nn 1+()
2
-----------------------
nn 1+()2n 1+()
6
---------------------------------------------- -
n
2
n 1+()
2
4
---------------------------- -
§ 41. Разные задачи 199
Используя равенства (3)—(5) и формулы для сумм n чле-
нов арифметичесой и еометричесой прорессий, вычислите
предел:
24.
25. + + ... + .
26. + + + ... + .
27. – .
28. + + ... + + .
29. + + ... + .
30. + + ... + .
31. + + ... + , де (a
n
)— арифме-
тичесая прорессия с разностью d, члены оторой отличны
от нуля.
32. + + ... + .
Найдите предел последовательности:
33. a
n
= · ... (в последнем
сомножителе n радиалов).
34. a
n
= (n радиалов).
35. a
n
= (n радиалов).
n º×
lim
1 2 ... + 2
n
++
1 5 ... + 5
n
++
----------------------------------------- .
n º×
lim
1
n
2
------
2
n
2
------
n 1–
n
2
-------------
n º×
lim
3
1
3
-------
1
33
-----------
3
3
n 1–
------------- -
n º×
lim
1 3 5 ... 2n 1+()+++ +
n 1+
--------------------------------------------------------------------
2n 1–
2
-----------------
n º×
lim
1
2
n
3
------
2
2
n
3
------
n 1–()
2
n
3
---------------------
1
n
---
n º×
lim
7
10
------
29
10
2
---------
5
n
2
n
+
10
n
------------------- -
n º×
lim
1
12⋅
-----------
1
23⋅
-----------
1
nn 1+()
-----------------------
n º×
lim
1
a
1
a
2
-------------
1
a
2
a
3
-------------
1
a
n
a
n 1+
---------------------
n º×
lim
1
n
4
------
8
n
4
------
n
3
n
4
------
2
2
-------
2
22+
----------------------
2
2 2 ... 2 2++++
-----------------------------------------------------------------
aa... a+++
22...2++–
2 2 ... 3++–
------------------------------------------------- -
