Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


Глава 6
Комплексные числа
§ 31. Действия с комплексными числами
Запись числа z в виде a + bi, де a и b— действительные
числа, а число i удовлетворяет равенству i
2
= –1, называют ал-
ебраичесой формой омплесноо числа. Число a называют
действительной частью омплесноо числа и обозначают
Re z, число b— мнимой частью омплесноо числа и обо-
значают Im z. Символ i называют мнимой единицей.
Два омплесных числа z
1
= a
1
+ b
1
i и z
2
= a
2
+ b
2
i равны,
если a
1
= a
2
и b
1
= b
2
.
Комплесное число –a – bi называют противоположным
омплесному числу a + bi.
Рассмотрим правила действий с омплесными числами.
Пусть z
1
= a
1
+ b
1
i и z
2
= a
2
+ b
2
i— два омплесных числа.
Смма z
1
+ z
2
, разность z
1
– z
2
, произведение z
1
z
2
и част-
ное (z
2
− 0) омплесных чисел z
1
и z
2
вычисляются по фор-
мулам
z
1
+ z
2
= (a
1
+ a
2
) + (b
1
+ b
2
)i,
z
1
– z
2
= (a
1
– a
2
) + (b
1
– b
2
)i,
z
1
z
2
= (a
1
a
2
– b
1
b
2
) + (a
1
b
2
+ a
2
b
1
)i,(1)
= +
Сложение и умножение омплесных чисел оммутативно и
ассоциативно, умножение дистрибутивно относительно сло-
жения.
Комплесное число a – bi называют омплесно сопряжен-
ным с числом z = a + bi и обозначают . Комплесно сопря-
женные числа z и обладают следующим свойством:
z
·
= a
2
+ b
2
.
Пусть z = a + bi — отличное от нуля (т. е. a
2
+ b
2
− 0) омп-
лесное число. Модлем омплесноо числа (обозначение:
z
1
z
2
-----
z
1
z
2
-----
a
1
b
2
a
2
b
1
+
a
2
2
b
2
2
+
--------------------------------
a
2
b
1
a
1
b
2
–
a
2
2
b
2
2
+
------------------------------- i.
z
z
z
§ 31. Действия с комплексными числами 161
|z| или r) называют величину . Арментом омп-
лесноо числа z называют уол ϕ, определяемый из условий
sin ϕ = , cos ϕ =
(обозначение: Arg z или ϕ). Главным значением армента
омплесноо числа z (обозначение: arg z) называют значение
ϕ, принадлежащее промежуту (–π; π].
Запись омплесноо числа z = a + bi
в виде
z = r (cos ϕ + i sin ϕ)
называют трионометричесой формой
омплесноо числа.
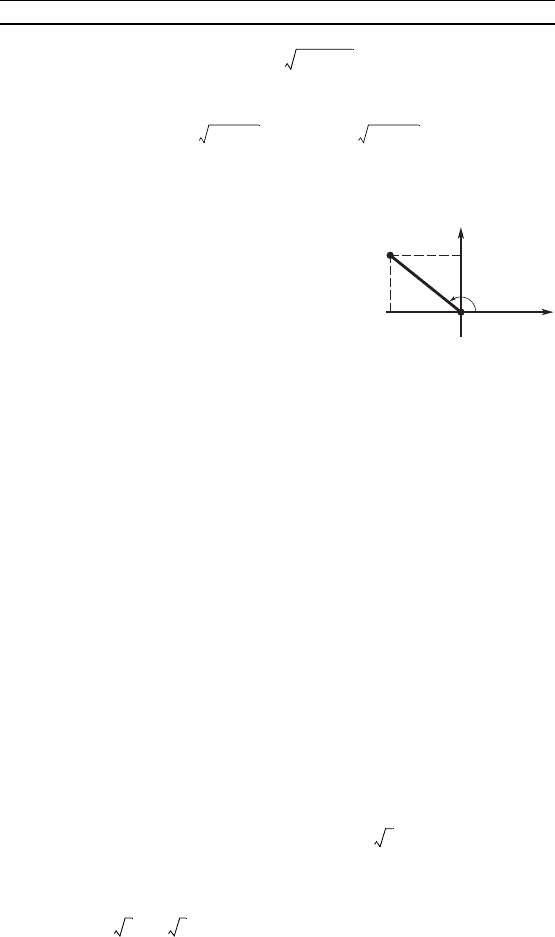
Геометричеси модуль омплесно-
о числа можно изобразить а отре-
зо (радиус-ветор) длины r, имеющий
своими онцами точи (0; 0) и (a; b); арумент омплесноо
числа — а уол, оторый образует радиус-ветор с положи-
тельным направлением оси Ox (рис. 9).
Два омплесных числа, записанные в трионометричесой
форме, равны тода и тольо тода, ода равны их модули, а
арументы отличаются на 2πk (k Ý Z).
Произведением и частным двух отличных от нуля омп-
лесных чисел z
1
= r
1
(cos ϕ
1
+ i sin ϕ
1
) и z
2
= r
2
(cos ϕ
2
+ i sin ϕ
2
),
записанных в трионометричесой форме, являются числа
z
1
z
2
= r
1
r
2
[cos (ϕ
1
+ ϕ
2
) + i sin (ϕ
1
+ ϕ
2
)],
= [cos (ϕ
1
– ϕ
2
) + i sin (ϕ
1
– ϕ
2
)],
а n-я степень омплесноо числа z = r (cos ϕ + i sin ϕ) вычис-
ляется по формле Мавра
z
n
= r
n
(cos nϕ + i sin nϕ). (2)
Корнем n-й степени из омплесноо числа z называют
омплесное число w, удовлетворяющее уравнению
w
n
= z.
Все решения этоо уравнения обозначают и для числа z, за-
писанноо в трионометричесой форме z = r (cos ϕ + i sin ϕ),
эти решения вычисляют по формуле
= cos + i sin , (3)
де k = 0, 1, 2, ..., n – 1.
a
2
b
2
+
b
a
2
b
2
+
-----------------------
a
a
2
b
2
+
-----------------------
x
a
y
b
|z|
ϕ = arg z
O
Рис. 9
z
1
z
2
-----
r
1
r
2
-----
z
n
z
n
r
n
ϕ 2πk+
n
---------------------
ϕ 2πk+
n
---------------------
Глава 6
Комплексные числа
§ 31. Действия с комплексными числами
Запись числа z в виде a + bi, де a и b— действительные
числа, а число i удовлетворяет равенству i
2
= –1, называют ал-
ебраичесой формой омплесноо числа. Число a называют
действительной частью омплесноо числа и обозначают
Re z, число b— мнимой частью омплесноо числа и обо-
значают Im z. Символ i называют мнимой единицей.
Два омплесных числа z
1
= a
1
+ b
1
i и z
2
= a
2
+ b
2
i равны,
если a
1
= a
2
и b
1
= b
2
.
Комплесное число –a – bi называют противоположным
омплесному числу a + bi.
Рассмотрим правила действий с омплесными числами.
Пусть z
1
= a
1
+ b
1
i и z
2
= a
2
+ b
2
i— два омплесных числа.
Смма z
1
+ z
2
, разность z
1
– z
2
, произведение z
1
z
2
и част-
ное (z
2
− 0) омплесных чисел z
1
и z
2
вычисляются по фор-
мулам
z
1
+ z
2
= (a
1
+ a
2
) + (b
1
+ b
2
)i,
z
1
– z
2
= (a
1
– a
2
) + (b
1
– b
2
)i,
z
1
z
2
= (a
1
a
2
– b
1
b
2
) + (a
1
b
2
+ a
2
b
1
)i,(1)
= +
Сложение и умножение омплесных чисел оммутативно и
ассоциативно, умножение дистрибутивно относительно сло-
жения.
Комплесное число a – bi называют омплесно сопряжен-
ным с числом z = a + bi и обозначают . Комплесно сопря-
женные числа z и обладают следующим свойством:
z
·
= a
2
+ b
2
.
Пусть z = a + bi — отличное от нуля (т. е. a
2
+ b
2
− 0) омп-
лесное число. Модлем омплесноо числа (обозначение:
z
1
z
2
-----
z
1
z
2
-----
a
1
b
2
a
2
b
1
+
a
2
2
b
2
2
+
--------------------------------
a
2
b
1
a
1
b
2
–
a
2
2
b
2
2
+
------------------------------- i.
z
z
z
§ 31. Действия с комплексными числами 161
|z| или r) называют величину . Арментом омп-
лесноо числа z называют уол ϕ, определяемый из условий
sin ϕ = , cos ϕ =
(обозначение: Arg z или ϕ). Главным значением армента
омплесноо числа z (обозначение: arg z) называют значение
ϕ, принадлежащее промежуту (–π; π].
Запись омплесноо числа z = a + bi
в виде
z = r (cos ϕ + i sin ϕ)
называют трионометричесой формой
омплесноо числа.
Геометричеси модуль омплесно-
о числа можно изобразить а отре-
зо (радиус-ветор) длины r, имеющий
своими онцами точи (0; 0) и (a; b); арумент омплесноо
числа — а уол, оторый образует радиус-ветор с положи-
тельным направлением оси Ox (рис. 9).
Два омплесных числа, записанные в трионометричесой
форме, равны тода и тольо тода, ода равны их модули, а
арументы отличаются на 2πk (k Ý Z).
Произведением и частным двух отличных от нуля омп-
лесных чисел z
1
= r
1
(cos ϕ
1
+ i sin ϕ
1
) и z
2
= r
2
(cos ϕ
2
+ i sin ϕ
2
),
записанных в трионометричесой форме, являются числа
z
1
z
2
= r
1
r
2
[cos (ϕ
1
+ ϕ
2
) + i sin (ϕ
1
+ ϕ
2
)],
= [cos (ϕ
1
– ϕ
2
) + i sin (ϕ
1
– ϕ
2
)],
а n-я степень омплесноо числа z = r (cos ϕ + i sin ϕ) вычис-
ляется по формле Мавра
z
n
= r
n
(cos nϕ + i sin nϕ). (2)
Корнем n-й степени из омплесноо числа z называют
омплесное число w, удовлетворяющее уравнению
w
n
= z.
Все решения этоо уравнения обозначают и для числа z, за-
писанноо в трионометричесой форме z = r (cos ϕ + i sin ϕ),
эти решения вычисляют по формуле
= cos + i sin , (3)
де k = 0, 1, 2, ..., n – 1.
a
2
b
2
+
b
a
2
b
2
+
-----------------------
a
a
2
b
2
+
-----------------------
x
a
y
b
|z|
ϕ = arg z
O
Рис. 9
z
1
z
2
-----
r
1
r
2
-----
z
n
z
n
r
n
ϕ 2πk+
n
---------------------
ϕ 2πk+
n
---------------------
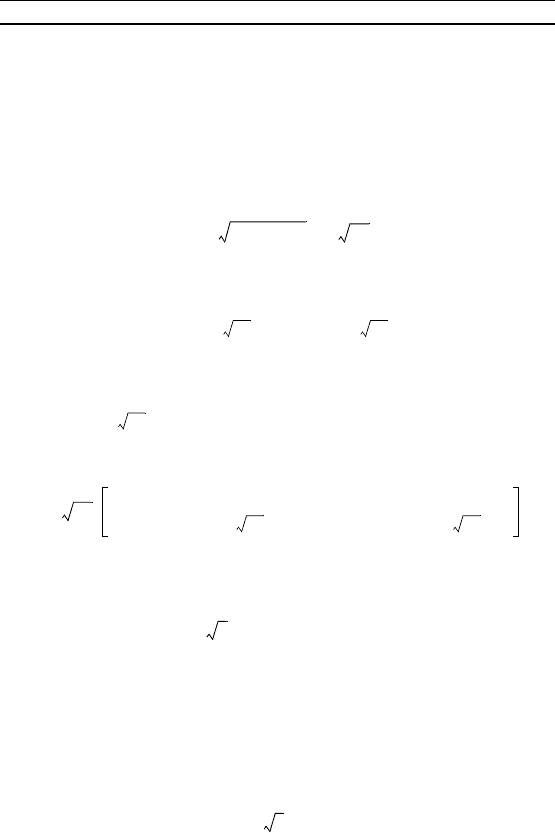
162 Г л а в а 6. Комплексные числа
Действия с омплесными числами выполняют по форму-
лам (1). При вычислении произведения и частноо омплес-
ных чисел удобно использовать представление омплесных чи-
сел в трионометричесой форме.
П р и м е р 1. Представить в трионометричесой форме
омплесное число z = –3 + i.
Р е ш е н и е. По определению модуля омплесноо числа
имеем
|z| = = .
Обозначив арумент омплесноо числа через ϕ, получаем
sin ϕ = , cos ϕ = – ,
отуда следует, что уол ϕ принадлежит второй четверти и ра-
вен arccos – . Следовательно, запись омплесноо числа
z = –3 + i в трионометричесой форме имеет вид
z = cos arccos – + i sin arccos – .
Представьте в трионометричесой форме омплесное число:
1. 1. 2. –3. 3. i. 4. 1 + i.
5. –1 + i. 6. 1 + i . 7. 3 – 4i. 8. –3 – 4i.
9. –cos + i sin . 10. sin α – i cos α. 11. .
Для вычисления орней k-й степени из омплесноо числа
обычно используют представление омплесных чисел в трио-
нометричесой форме.
Пример 2. Вычислить .
Р е ш е н и е. Запишем омплесное число i = 0 + 1 · i в три-
онометричесой форме. Та а | i | = 1, arg i = , то трионо-
метричесая форма числа i имеет вид
i = cos + i sin .
3–()
2
1+ 10
1
10
---------- -
3
10
---------- -
3
10
---------- -
10
3
10
---------- -
3
10
---------- -
3
π
3
---
π
3
---
1
i 1–
----------- -
100
i
3
π
2
---
π
2
---
π
2
---
§ 32. Геом. изображение некоторых множеств комплексных чисел 163
Отсюда, соласно формуле (3), получаем
r = = 1, ϕ = + ,
де k = 0, k = 1, k = 2. Ита, исомыми орнями являются сле-
дующие омплесные числа:
cos + i sin = + i,
cos + i sin = – + i,
cos + i sin = –i.
Геометричеси полученные орни пред-
ставляют собой точи, лежащие на еди-
ничной оружности (та а r = 1), ра-
диус-веторы оторых составляют улы
, и с положительным направле-
нием оси Ox (рис. 10).
Ответ. ä + i; –i.
Используя трионометричесую форму записи омплесно-
о числа, вычислите:
12. . 13. . 14. . 15. .
16. . 17. . 18. . 19. .
§ 32. Геометрическое изображение
множеств комплексных чисел,
удовлетворяющих заданным условиям
Для еометричесоо изображения омплесных чисел, удов-
летворяющих неоторым соотношениям, обычно используют
алебраичесую форму омплесноо числа.
1
3
π
6
---
2πk
3
---------- -
x
y
O 1
1
5π
6
3π
2
π
6
Рис. 10
π
6
---
π
6
---
3
2
-------
1
2
---
5π
6
------ -
5π
6
------ -
3
2
-------
1
2
---
3π
2
------ -
3π
2
------ -
π
6
---
5π
6
------ -
3π
2
------ -
3
2
-------
1
2
---
2i 8i– 34i– 1–
4
22i 3–
4
i
4
34i+
7
1
3
162 Г л а в а 6. Комплексные числа
Действия с омплесными числами выполняют по форму-
лам (1). При вычислении произведения и частноо омплес-
ных чисел удобно использовать представление омплесных чи-
сел в трионометричесой форме.
П р и м е р 1. Представить в трионометричесой форме
омплесное число z = –3 + i.
Р е ш е н и е. По определению модуля омплесноо числа
имеем
|z| = = .
Обозначив арумент омплесноо числа через ϕ, получаем
sin ϕ = , cos ϕ = – ,
отуда следует, что уол ϕ принадлежит второй четверти и ра-
вен arccos – . Следовательно, запись омплесноо числа
z = –3 + i в трионометричесой форме имеет вид
z = cos arccos – + i sin arccos – .
Представьте в трионометричесой форме омплесное число:
1. 1. 2. –3. 3. i. 4. 1 + i.
5. –1 + i. 6. 1 + i . 7. 3 – 4i. 8. –3 – 4i.
9. –cos + i sin . 10. sin α – i cos α. 11. .
Для вычисления орней k-й степени из омплесноо числа
обычно используют представление омплесных чисел в трио-
нометричесой форме.
Пример 2. Вычислить .
Р е ш е н и е. Запишем омплесное число i = 0 + 1 · i в три-
онометричесой форме. Та а | i | = 1, arg i = , то трионо-
метричесая форма числа i имеет вид
i = cos + i sin .
3–()
2
1+ 10
1
10
---------- -
3
10
---------- -
3
10
---------- -
10
3
10
---------- -
3
10
---------- -
3
π
3
---
π
3
---
1
i 1–
----------- -
100
i
3
π
2
---
π
2
---
π
2
---
§ 32. Геом. изображение некоторых множеств комплексных чисел 163
Отсюда, соласно формуле (3), получаем
r = = 1, ϕ = + ,
де k = 0, k = 1, k = 2. Ита, исомыми орнями являются сле-
дующие омплесные числа:
cos + i sin = + i,
cos + i sin = – + i,
cos + i sin = –i.
Геометричеси полученные орни пред-
ставляют собой точи, лежащие на еди-
ничной оружности (та а r = 1), ра-
диус-веторы оторых составляют улы
, и с положительным направле-
нием оси Ox (рис. 10).
Ответ. ä + i; –i.
Используя трионометричесую форму записи омплесно-
о числа, вычислите:
12. . 13. . 14. . 15. .
16. . 17. . 18. . 19. .
§ 32. Геометрическое изображение
множеств комплексных чисел,
удовлетворяющих заданным условиям
Для еометричесоо изображения омплесных чисел, удов-
летворяющих неоторым соотношениям, обычно используют
алебраичесую форму омплесноо числа.
1
3
π
6
---
2πk
3
---------- -
x
y
O 1
1
5π
6
3π
2
π
6
Рис. 10
π
6
---
π
6
---
3
2
-------
1
2
---
5π
6
------ -
5π
6
------ -
3
2
-------
1
2
---
3π
2
------ -
3π
2
------ -
π
6
---
5π
6
------ -
3π
2
------ -
3
2
-------
1
2
---
2i 8i– 34i– 1–
4
22i 3–
4
i
4
34i+
7
1
3

164 Г л а в а 6. Комплексные числа
П р и м е р 1. Найти множество точе оординатной плос-
ости xOy, изображающих омплесные числа z, для оторых
| z + i – 2 | m 2.
Р е ш е н и е. Алебраичесая форма омплесноо числа z
имеет вид z = x + iy. Тода
z + i – 2 = (x – 2) + (y + 1)i.
Соласно определению модуля омплесноо числа, имеем
| z + i – 2 | = .
Поэтому неравенство | z + i – 2 | m 2 примет вид
m 2 _ + m
Множество точе оординатной плосости xOy, удовлетворяю-
щих последнему неравенству, представляет собой множество
всех точе, лежащих внутри и на ранице оружности с цент-
ром в точе (2; –1) и радиусом 2.
П р и м е р 2. Найти множество точе оординатной плос-
ости xOy, для оторых действительная часть омплесноо
числа (1 + i)z
2
положительна.
Р е ш е н и е. Представив омплесное число z в алебраи-
чесой форме, имеем z = x + iy. Следовательно,
z
2
= x
2
– y
2
+ 2xyi,
(1 + i)z
2
= (1 + i)(x
2
– y
2
+ 2xyi) =
= (x
2
– 2xy – y
2
) + (x
2
+ 2xy – y
2
)i.
По условию действительная часть омплесноо числа (1 + i)z
2
положительна:
x
2
– 2xy – y
2
> 0. (*)
Предполаая, что y − 0, и разделив обе части неравенства (*)
на y
2
, получаем
– 2 – 1 > 0.
Решив это вадратное неравенство, находим
> 1 + , < 1 – . (**)
Если y > 0, то неравенства (**) можно записать в виде
y < x, y < x.
x 2–()
2
y 1+()
2
+
(x 2)
2
–(y 1)
2
++ (x 2)
2
–(y 1)
2
+2
2
.
x
y
---
2
x
y
---
x
y
---
2
x
y
---
2
1
12+
------------------
1
12–
-----------------
§ 32. Геом. изображение некоторых множеств комплексных чисел 165
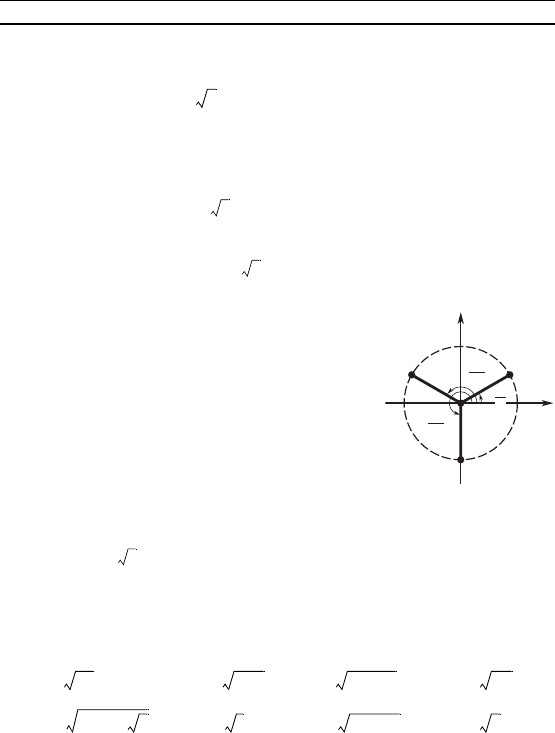
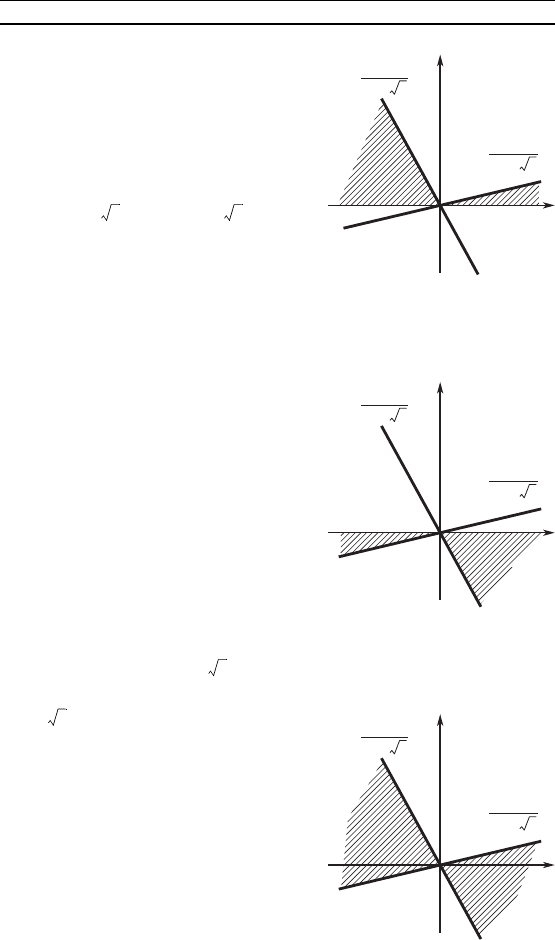
Множество точе плосости xOy,
удовлетворяющих этим неравенст-
вам (при y > 0), отмечено штри-
ховой на рис. 11.
Если y < 0, то неравенства (**)
примут вид
y > x, y > x,
и множество точе оординатной
плосости xOy, удовлетворяющих
этим неравенствам (при y < 0), от-
мечено штриховой на рис. 12.
Если y = 0, то нельзя разделить
обе части неравенства (*) на y
2
, но
при y = 0 неравенство (*) превра-
щается в неравенство x
2
> 0, ре-
шением отороо является любое
действительное число x, отличное
от нуля, т. е. решением неравенст-
ва (*) является любая точа оси Ox,
за ислючением нуля.
Объединяя все три случая,
оончательно получаем: исомым
множеством являются улы, содер-
жащие ось Ox, без своих раниц;
стороны этих улов представляют
собой прямые y = и y =
= (рис. 13).
Найдите множество точе о-
ординатной плосости xOy, изо-
бражающих омплесные числа
z = x + iy, для оторых:
1. | z | = 1. 2. z = | z |.
3. arg z = . 4. 1 < | z | < 2.
5. |2z – 1 | > 2.
6. ||z | + i | < 10.
7. | z + 1 | = | z – 1 |.
x
y
O
y = x
1 – 2
1
y = x
1 + 2
1
Рис. 11
x
y
O
y = x
1 – 2
1
y = x
1 + 2
1
x
y
O
y = x
1 – 2
1
y = x
1 + 2
1
Рис. 12
Рис. 13
1
12+
------------------
1
12–
-----------------
1
12+
------------------ x
1
12–
----------------- x
π
3
---
164 Г л а в а 6. Комплексные числа
П р и м е р 1. Найти множество точе оординатной плос-
ости xOy, изображающих омплесные числа z, для оторых
| z + i – 2 | m 2.
Р е ш е н и е. Алебраичесая форма омплесноо числа z
имеет вид z = x + iy. Тода
z + i – 2 = (x – 2) + (y + 1)i.
Соласно определению модуля омплесноо числа, имеем
| z + i – 2 | = .
Поэтому неравенство | z + i – 2 | m 2 примет вид
m 2 _ + m
Множество точе оординатной плосости xOy, удовлетворяю-
щих последнему неравенству, представляет собой множество
всех точе, лежащих внутри и на ранице оружности с цент-
ром в точе (2; –1) и радиусом 2.
П р и м е р 2. Найти множество точе оординатной плос-
ости xOy, для оторых действительная часть омплесноо
числа (1 + i)z
2
положительна.
Р е ш е н и е. Представив омплесное число z в алебраи-
чесой форме, имеем z = x + iy. Следовательно,
z
2
= x
2
– y
2
+ 2xyi,
(1 + i)z
2
= (1 + i)(x
2
– y
2
+ 2xyi) =
= (x
2
– 2xy – y
2
) + (x
2
+ 2xy – y
2
)i.
По условию действительная часть омплесноо числа (1 + i)z
2
положительна:
x
2
– 2xy – y
2
> 0. (*)
Предполаая, что y − 0, и разделив обе части неравенства (*)
на y
2
, получаем
– 2 – 1 > 0.
Решив это вадратное неравенство, находим
> 1 + , < 1 – . (**)
Если y > 0, то неравенства (**) можно записать в виде
y < x, y < x.
x 2–()
2
y 1+()
2
+
(x 2)
2
–(y 1)
2
++ (x 2)
2
–(y 1)
2
+2
2
.
x
y
---
2
x
y
---
x
y
---
2
x
y
---
2
1
12+
------------------
1
12–
-----------------
§ 32. Геом. изображение некоторых множеств комплексных чисел 165
Множество точе плосости xOy,
удовлетворяющих этим неравенст-
вам (при y > 0), отмечено штри-
ховой на рис. 11.
Если y < 0, то неравенства (**)
примут вид
y > x, y > x,
и множество точе оординатной
плосости xOy, удовлетворяющих
этим неравенствам (при y < 0), от-
мечено штриховой на рис. 12.
Если y = 0, то нельзя разделить
обе части неравенства (*) на y
2
, но
при y = 0 неравенство (*) превра-
щается в неравенство x
2
> 0, ре-
шением отороо является любое
действительное число x, отличное
от нуля, т. е. решением неравенст-
ва (*) является любая точа оси Ox,
за ислючением нуля.
Объединяя все три случая,
оончательно получаем: исомым
множеством являются улы, содер-
жащие ось Ox, без своих раниц;
стороны этих улов представляют
собой прямые y = и y =
= (рис. 13).
Найдите множество точе о-
ординатной плосости xOy, изо-
бражающих омплесные числа
z = x + iy, для оторых:
1. | z | = 1. 2. z = | z |.
3. arg z = . 4. 1 < | z | < 2.
5. |2z – 1 | > 2.
6. ||z | + i | < 10.
7. | z + 1 | = | z – 1 |.
x
y
O
y = x
1 – 2
1
y = x
1 + 2
1
Рис. 11
x
y
O
y = x
1 – 2
1
y = x
1 + 2
1
x
y
O
y = x
1 – 2
1
y = x
1 + 2
1
Рис. 12
Рис. 13
1
12+
------------------
1
12–
-----------------
1
12+
------------------ x
1
12–
----------------- x
π
3
---

166 Г л а в а 6. Комплексные числа
8. | z + i | = | z + 2 |. 9. | z + i | > | z |.
10. 1 m | z + i | m 4. 11. (1 – i) = (1 + i)z.
12. На оординатной плосости pOq изобразите множество
точе (p; q) таих, что орни уравнения x
2
+ px + q = 0 (воз-
можно, омплесные) по модулю не превосходят единицы.
13. Уажите все точи омплесной плосости таие, что:
а) zα; б) z + α — действительные числа (α = a + bi — заданное
омплесное число).
14. Найдите множество точе оординатной плосости xOy,
удовлетворяющих неравенству
log
1/2
> 1.
15. На оординатной плосости xOy найдите множество
всех точе, оординаты оторых удовлетворяют следующему
условию: z
2
+ z + 1 — действительное положительное число.
16. Изобразите на плосости все омплесные числа z, для
оторых число (1 + i)z является действительным.
17. Точи z
1
, z
2
, z
3
— вершины треуольниа. Каое омп-
лесное число соответствует центру тяжести этоо треуоль-
ниа?
18. Точи z
1
, z
2
, z
3
— три вершины параллелорамма. Най-
дите четвертую вершину.
19. Доажите, что три различные точи z
1
, z
2
, z
3
лежат на
одной прямой тода и тольо тода, ода — действи-
тельное число.
20. При аих z
1
и z
2
справедливо равенство
|z
1
+ z
2
| = |z
1
– z
2
|?
21. Доажите, что четырехуольни, сумма вадратов сто-
рон отороо равна сумме вадратов ео диаоналей, — парал-
лелорамм.
§ 33. Решение уравнений
на множестве комплексных чисел
Решение уравнения на множестве омплесных чисел сво-
дится решению системы уравнений на множестве действи-
тельных чисел; эта система получается в результате сравнения
z
z 1–4+
3 z 1–2–
----------------------------- -
z
3
z
1
–
z
2
z
1
–
------------------
§ 33. Решение уравнений на множестве комплексных чисел 167
действительных и мнимых частей выражений, входящих в ис-
ходное уравнение.
П р и м е р 1. Решить на множестве омплесных чисел
уравнение
2z = | z | + 2i.
Р е ш е н и е. Комплесное число z в алебраичесой форме
имеет вид z = x + iy, де x, y— действительные числа. Тода
| z | = и данное уравнение запишется та:
2x + 2iy = + 2i.
Соласно определению равенства двух омплесных чисел, по-
лучаем систему уравнений для нахождения x и y:
Из второо уравнения находим y = 1. Подставив y = 1 в первое
уравнение системы, получим уравнение 2x = , имею-
щее орень x = . Ита, решением данноо уравнения явля-
ется омплесное число z = + i.
Ответ. z = + i.
П р и м е р 2. Для аждоо действительноо числа a > 0
найти все омплесные числа z, удовлетворяющие равенству
z| z | + az + i = 0.
Р е ш е н и е. Записав омплесное число z в алебраиче-
сой форме, имеем z = x + iy. Тода | z | = и приходим
уравнению
(x + iy) + a(x + iy) + i = 0 _
_ (x + ax) + (y + ay + 1)i = 0 + 0 · i.
Соласно определению равенства двух омплесных чисел, за-
лючаем, что последнее уравнение эвивалентно системе двух
уравнений
(*)
x
2
y
2
+
x
2
y
2
+
2x – = 0,
2y – 2 = 0.
x
2
y
2
+
x
2
1+
1
3
-------
1
3
-------
1
3
-------
x
2
y
2
+
x
2
y
2
+
x
2
y
2
+ x
2
y
2
+
x + ax = 0,
y + ay + 1 = 0,
x
2
y
2
+
x
2
y
2
+
166 Г л а в а 6. Комплексные числа
8. | z + i | = | z + 2 |. 9. | z + i | > | z |.
10. 1 m | z + i | m 4. 11. (1 – i) = (1 + i)z.
12. На оординатной плосости pOq изобразите множество
точе (p; q) таих, что орни уравнения x
2
+ px + q = 0 (воз-
можно, омплесные) по модулю не превосходят единицы.
13. Уажите все точи омплесной плосости таие, что:
а) zα; б) z + α — действительные числа (α = a + bi — заданное
омплесное число).
14. Найдите множество точе оординатной плосости xOy,
удовлетворяющих неравенству
log
1/2
> 1.
15. На оординатной плосости xOy найдите множество
всех точе, оординаты оторых удовлетворяют следующему
условию: z
2
+ z + 1 — действительное положительное число.
16. Изобразите на плосости все омплесные числа z, для
оторых число (1 + i)z является действительным.
17. Точи z
1
, z
2
, z
3
— вершины треуольниа. Каое омп-
лесное число соответствует центру тяжести этоо треуоль-
ниа?
18. Точи z
1
, z
2
, z
3
— три вершины параллелорамма. Най-
дите четвертую вершину.
19. Доажите, что три различные точи z
1
, z
2
, z
3
лежат на
одной прямой тода и тольо тода, ода — действи-
тельное число.
20. При аих z
1
и z
2
справедливо равенство
|z
1
+ z
2
| = |z
1
– z
2
|?
21. Доажите, что четырехуольни, сумма вадратов сто-
рон отороо равна сумме вадратов ео диаоналей, — парал-
лелорамм.
§ 33. Решение уравнений
на множестве комплексных чисел
Решение уравнения на множестве омплесных чисел сво-
дится решению системы уравнений на множестве действи-
тельных чисел; эта система получается в результате сравнения
z
z 1–4+
3 z 1–2–
----------------------------- -
z
3
z
1
–
z
2
z
1
–
------------------
§ 33. Решение уравнений на множестве комплексных чисел 167
действительных и мнимых частей выражений, входящих в ис-
ходное уравнение.
П р и м е р 1. Решить на множестве омплесных чисел
уравнение
2z = | z | + 2i.
Р е ш е н и е. Комплесное число z в алебраичесой форме
имеет вид z = x + iy, де x, y— действительные числа. Тода
| z | = и данное уравнение запишется та:
2x + 2iy = + 2i.
Соласно определению равенства двух омплесных чисел, по-
лучаем систему уравнений для нахождения x и y:
Из второо уравнения находим y = 1. Подставив y = 1 в первое
уравнение системы, получим уравнение 2x = , имею-
щее орень x = . Ита, решением данноо уравнения явля-
ется омплесное число z = + i.
Ответ. z = + i.
П р и м е р 2. Для аждоо действительноо числа a > 0
найти все омплесные числа z, удовлетворяющие равенству
z| z | + az + i = 0.
Р е ш е н и е. Записав омплесное число z в алебраиче-
сой форме, имеем z = x + iy. Тода | z | = и приходим
уравнению
(x + iy) + a(x + iy) + i = 0 _
_ (x + ax) + (y + ay + 1)i = 0 + 0 · i.
Соласно определению равенства двух омплесных чисел, за-
лючаем, что последнее уравнение эвивалентно системе двух
уравнений
(*)
x
2
y
2
+
x
2
y
2
+
2x – = 0,
2y – 2 = 0.
x
2
y
2
+
x
2
1+
1
3
-------
1
3
-------
1
3
-------
x
2
y
2
+
x
2
y
2
+
x
2
y
2
+ x
2
y
2
+
x + ax = 0,
y + ay + 1 = 0,
x
2
y
2
+
x
2
y
2
+

168 Г л а в а 6. Комплексные числа
решения оторой следует исать на множестве действительных
чисел.
Нетрудно заметить, что множество решений первоо урав-
нения системы (*) можно найти а объединение множеств ре-
шений двух уравнений:
x = 0, + a = 0.
Второе из этих уравнений не имеет решений, та а по усло-
вию a > 0. Подставив x = 0 во второе уравнение системы (*),
для действительноо числа y получаем уравнение
y|y| + ay + 1 = 0.
Множество решений этоо уравнения получается а объеди-
нение множеств решений двух систем:
Учитывая условие a > 0, лео убедиться в том, что первая сис-
тема не имеет решений, а вторая имеет единственное решение:
y = . Ита, решением данноо уравнения является
чисто мнимое число z = i.
Ответ. z = i.
Решите уравнение:
1. (2 + i)z
2
– (5 – i)z + 2 – 2i = 0. 2. z
2
+ = 0.
3. | z | – iz = 1 – 2i. 4. z
2
= ( )
3
.
5. (x + y)
2
+ 6 + ix = 5(x + y) + i (y + 1) (x, y— действитель-
ные числа).
6. При аих действительных значениях x и y справедливо
равенство
= 1 – 3i?
7. Доажите, что уравнение z
3
+ iz – 1 = 0 не имеет действи-
тельных орней.
8. Вычислите z
14
+ , если z— орень уравнения z + = 1.
x
2
y
2
+
y l 0,
y
2
+ ay + 1 = 0;
y < 0,
–y
2
+ ay + 1 = 0.
aa
2
4+–
2
-------------------------------
aa
2
4+–
2
-------------------------------
aa
2
4+–
2
-------------------------------
z
z
x 2– y 3–()i+
1 i+
-----------------------------------------
1
z
14
--------
1
z
---
§ 33. Решение уравнений на множестве комплексных чисел 169
19. Решите на множестве омплесных чисел уравнение
z
3
– z
2
+ z – 1 = 0.
10. Решите на множестве омплесных чисел систему урав-
нений:
а) б)
11. Каому условию должно удовлетворять омплесное
число a + bi для тоо чтобы ео можно было представить в виде
a + bi = ,
де x— действительное число?
12. Среди омплесных чисел z найдите все таие числа,
для оторых
log
14
(13 + | z
2
– 4i |) + log
196
= 0.
13. Для аждоо действительноо числа a l 1 найдите все
омплесные числа z, удовлетворяющие уравнению
z + a|z + 1| + i = 0.
14. При аих действительных значениях параметра a
хотя бы одно омплесное число z = x + iy, удовлетворяющее
равенству
| z + | = a
2
– 3a + 2,
удовлетворяет одновременно и неравенству
| z + i | < a
2
?
15. При аих действительных значениях параметра a
хотя бы одно омплесное число z = x + iy, удовлетворяющее
равенству
| z – ai | = a + 4,
удовлетворяет одновременно и неравенству
| z – 2 | < 1?
16. Найдите наименьшее по модулю омплесное число z,
удовлетворяющее условию | z – 2 + 2i | = 1.
z
5
w
7
= 1,
z
2
–
3
= 0;w
z
13
w
19
= 1,
z
5
w
7
= 1,
z
2
+ w
2
= –2.
1 ix–
1 ix+
----------------
1
(13 | z
2
4i |)
2
++
----------------------------------------------
2
2

168 Г л а в а 6. Комплексные числа
решения оторой следует исать на множестве действительных
чисел.
Нетрудно заметить, что множество решений первоо урав-
нения системы (*) можно найти а объединение множеств ре-
шений двух уравнений:
x = 0, + a = 0.
Второе из этих уравнений не имеет решений, та а по усло-
вию a > 0. Подставив x = 0 во второе уравнение системы (*),
для действительноо числа y получаем уравнение
y|y| + ay + 1 = 0.
Множество решений этоо уравнения получается а объеди-
нение множеств решений двух систем:
Учитывая условие a > 0, лео убедиться в том, что первая сис-
тема не имеет решений, а вторая имеет единственное решение:
y = . Ита, решением данноо уравнения является
чисто мнимое число z = i.
Ответ. z = i.
Решите уравнение:
1. (2 + i)z
2
– (5 – i)z + 2 – 2i = 0. 2. z
2
+ = 0.
3. | z | – iz = 1 – 2i. 4. z
2
= ( )
3
.
5. (x + y)
2
+ 6 + ix = 5(x + y) + i (y + 1) (x, y— действитель-
ные числа).
6. При аих действительных значениях x и y справедливо
равенство
= 1 – 3i?
7. Доажите, что уравнение z
3
+ iz – 1 = 0 не имеет действи-
тельных орней.
8. Вычислите z
14
+ , если z— орень уравнения z + = 1.
x
2
y
2
+
y l 0,
y
2
+ ay + 1 = 0;
y < 0,
–y
2
+ ay + 1 = 0.
aa
2
4+–
2
-------------------------------
aa
2
4+–
2
-------------------------------
aa
2
4+–
2
-------------------------------
z
z
x 2– y 3–()i+
1 i+
-----------------------------------------
1
z
14
--------
1
z
---
§ 33. Решение уравнений на множестве комплексных чисел 169
19. Решите на множестве омплесных чисел уравнение
z
3
– z
2
+ z – 1 = 0.
10. Решите на множестве омплесных чисел систему урав-
нений:
а) б)
11. Каому условию должно удовлетворять омплесное
число a + bi для тоо чтобы ео можно было представить в виде
a + bi = ,
де x— действительное число?
12. Среди омплесных чисел z найдите все таие числа,
для оторых
log
14
(13 + | z
2
– 4i |) + log
196
= 0.
13. Для аждоо действительноо числа a l 1 найдите все
омплесные числа z, удовлетворяющие уравнению
z + a|z + 1| + i = 0.
14. При аих действительных значениях параметра a
хотя бы одно омплесное число z = x + iy, удовлетворяющее
равенству
| z + | = a
2
– 3a + 2,
удовлетворяет одновременно и неравенству
| z + i | < a
2
?
15. При аих действительных значениях параметра a
хотя бы одно омплесное число z = x + iy, удовлетворяющее
равенству
| z – ai | = a + 4,
удовлетворяет одновременно и неравенству
| z – 2 | < 1?
16. Найдите наименьшее по модулю омплесное число z,
удовлетворяющее условию | z – 2 + 2i | = 1.
z
5
w
7
= 1,
z
2
–
3
= 0;w
z
13
w
19
= 1,
z
5
w
7
= 1,
z
2
+ w
2
= –2.
1 ix–
1 ix+
----------------
1
(13 | z
2
4i |)
2
++
----------------------------------------------
2
2
