Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


150 Г л а в а 5. Тригонометрия
22. arccos x = arctg .
23. arcsin (2x ) = arccos (2x
2
– 1).
24. 2 arccos x = arccos (2x
2
– 1).
25. 2 arctg x = arcsin .
26. 2 arctg x = arccos .
27. arccos x = arcctg .
28. 2 arccos x = arcctg .
29. Решите уравнение arcsin x = 2 arcsin a при всех действи-
тельных значениях a.
30. Решите уравнение arccos x = arcsin 2a при всех действи-
тельных значениях a.
§ 28. Тригонометрические неравенства
Решения простейших трионометричесих неравенств при-
ведены в таблице:
Неравенство Решение неравенства (n Ý Z)
sin x > a (| a | < 1) x Ý (arcsin a + 2πn; π – arcsin a + 2πn)
sin x < a (| a | < 1) x Ý (–π – arcsin a + 2πn; arcsin a + 2πn)
cos x > a (| a | < 1) x Ý (–arccos a + 2πn; arccos a + 2πn)
cos x < a (| a | < 1) x Ý (arccos a + 2πn; 2π – arccos a + 2πn)
tg x > ax Ý arctg a + πn; + πn
tg x < ax Ý – + πn; arctg a + πn
ctg x > ax Ý (πn; arcctg a + πn)
ctg x < ax Ý (arcctg a + πn; π + πn)
1 x
2
–
x
--------------------
1 x
2
–
2x
1 x
2
+
---------------- -
1 x
2
–
1 x
2
+
---------------- -
x
1 x
2
–
--------------------
2x
2
1–
2x 1 x
2
–
----------------------------
π
2
---
π
2
---
§ 28. Тригонометрические неравенства 151
Решите неравенство:
1. sin x > – 0,5. 2. tg x > 2.
3. ctg x > –3. 4. sin (x – 1) m – 0,5 .
5. sin x
2
m 0,5. 6. sin x + cos x > – .
7. cos sin x < 0. 8. sin cos x l 0.
Неравенства вида R(y) > 0, R(y) < 0, де R— неоторая ра-
циональная фунция, а y— одна из трионометричесих
фунций (синус, осинус, таненс или отаненс), решают
в два этапа: сначала — рациональное неравенство относитель-
но неизвестноо y, а затем — простейшее трионометричесое
неравенство.
П р и м е р 1. Решить неравенство
2sin
2
x – 7 sin x + 3 > 0.
Р е ш е н и е. Полаая sin x = y, получим неравенство
2y
2
– 7y + 3 > 0,
имеющее множество решений y < , y > 3. Возвращаясь ис-
ходному неизвестному, залючаем, что данное неравенство э-
вивалентно двум неравенствам
sin x < , sin x > 3.
Второе неравенство не имеет решений, а решение первоо таово:
x Ý – + 2πn; + 2πn , n Ý Z.
Ответ. x Ý – + 2πn; + 2πn , n Ý Z.
Решите неравенство:
9. ctg
3
x + ctg
2
x – ctg x – 1 < 0.
10. 2cos2x + sin 2x > tg x.
11. tg x + ctg x < –3.
12. sin 2x > cos x.
13. cos x + cos x < 0.
14. > 2 sin x + 1.
3
2
1
2
---
1
2
---
7π
6
------ -
π
6
---
7π
6
------ -
π
6
---
3
34cos
2
x–

150 Г л а в а 5. Тригонометрия
22. arccos x = arctg .
23. arcsin (2x ) = arccos (2x
2
– 1).
24. 2 arccos x = arccos (2x
2
– 1).
25. 2 arctg x = arcsin .
26. 2 arctg x = arccos .
27. arccos x = arcctg .
28. 2 arccos x = arcctg .
29. Решите уравнение arcsin x = 2 arcsin a при всех действи-
тельных значениях a.
30. Решите уравнение arccos x = arcsin 2a при всех действи-
тельных значениях a.
§ 28. Тригонометрические неравенства
Решения простейших трионометричесих неравенств при-
ведены в таблице:
Неравенство Решение неравенства (n Ý Z)
sin x > a (| a | < 1) x Ý (arcsin a + 2πn; π – arcsin a + 2πn)
sin x < a (| a | < 1) x Ý (–π – arcsin a + 2πn; arcsin a + 2πn)
cos x > a (| a | < 1) x Ý (–arccos a + 2πn; arccos a + 2πn)
cos x < a (| a | < 1) x Ý (arccos a + 2πn; 2π – arccos a + 2πn)
tg x > ax Ý arctg a + πn; + πn
tg x < ax Ý – + πn; arctg a + πn
ctg x > ax Ý (πn; arcctg a + πn)
ctg x < ax Ý (arcctg a + πn; π + πn)
1 x
2
–
x
--------------------
1 x
2
–
2x
1 x
2
+
---------------- -
1 x
2
–
1 x
2
+
---------------- -
x
1 x
2
–
--------------------
2x
2
1–
2x 1 x
2
–
----------------------------
π
2
---
π
2
---
§ 28. Тригонометрические неравенства 151
Решите неравенство:
1. sin x > – 0,5. 2. tg x > 2.
3. ctg x > –3. 4. sin (x – 1) m – 0,5 .
5. sin x
2
m 0,5. 6. sin x + cos x > – .
7. cos sin x < 0. 8. sin cos x l 0.
Неравенства вида R(y) > 0, R(y) < 0, де R— неоторая ра-
циональная фунция, а y— одна из трионометричесих
фунций (синус, осинус, таненс или отаненс), решают
в два этапа: сначала — рациональное неравенство относитель-
но неизвестноо y, а затем — простейшее трионометричесое
неравенство.
П р и м е р 1. Решить неравенство
2sin
2
x – 7 sin x + 3 > 0.
Р е ш е н и е. Полаая sin x = y, получим неравенство
2y
2
– 7y + 3 > 0,
имеющее множество решений y < , y > 3. Возвращаясь ис-
ходному неизвестному, залючаем, что данное неравенство э-
вивалентно двум неравенствам
sin x < , sin x > 3.
Второе неравенство не имеет решений, а решение первоо таово:
x Ý – + 2πn; + 2πn , n Ý Z.
Ответ. x Ý – + 2πn; + 2πn , n Ý Z.
Решите неравенство:
9. ctg
3
x + ctg
2
x – ctg x – 1 < 0.
10. 2cos2x + sin 2x > tg x.
11. tg x + ctg x < –3.
12. sin 2x > cos x.
13. cos x + cos x < 0.
14. > 2 sin x + 1.
3
2
1
2
---
1
2
---
7π
6
------ -
π
6
---
7π
6
------ -
π
6
---
3
34cos
2
x–

152 Г л а в а 5. Тригонометрия
15. > 4 sin x + 1.
16. < 0.
17. < 4tg x.
18. 5 + 2 cos 2x m 3 |2 sin x – 1|.
В неоторых случаях при решении неравенств используют
разложение на множители.
П р и м е р 2. Решить неравенство
cos x + cos 2x + cos 3x > 0.
Р е ш е н и е. Преобразуя сумму райних слааемых в про-
изведение, получаем неравенство
cos 2x + 2 cos 2x cos x > 0,
или
cos 2x (2 cos x + 1) > 0.
Последнее неравенство эвивалентно двум системам про-
стейших неравенств:
Объединяя решения этих систем, находим решение исходноо
неравенства.
Ответ.– + 2πn; + 2πn Ÿ + 2πn; + 2πn Ÿ
Ÿ + 2πn; + 2πn , n Ý Z.
Решите неравенство:
19. sin x sin 2x – cos x cos 2x > sin 6x.
20. 2sinx sin 2x sin 3x < sin 4x.
21. sin x sin 3x > sin 5x sin 7x.
22. cos
3
x sin 3x + cos 3x sin
3
x < .
23. sin x l cos 2x.
24. 2tg2x m 3 tg x.
25. sin x < | cos x |.
3sinx 1+
2 sin
2
x sin x 1–+
sin x 1–
----------------------------------------------------
3
cos
2
x
---------------
cos 2x < 0,
cos x < – ;
1
2
---
cos 2x > 0,
cos x > – .
1
2
---
π
4
---
π
4
---
2π
3
------ -
3π
4
------ -
5π
4
------ -
4π
3
------ -
3
8
---
§ 29. Неравенства, содержащие обратные тригоном. функции 153
§ 29. Неравенства, содержащие
обратные тригонометрические функции
Решение простейших неравенств, содержащих обратные три-
онометричесие фунции, приведено в таблице:
Решите неравенство:
1. arcsin x m 5. 2. arcsin x l –2.
3. arccos x m arccos . 4. arccos x > .
5. arctg x > – . 6. arcctg x > 2.
Неравенства вида R(y) > 0, R(y) < 0, де R— неоторая ра-
циональная фунция, а y— одна из обратных трионометри-
чесих фунций (арсинус, аросинус, артаненс, аротан-
енс), решают в два этапа: сначала — неравенство относительно
неизвестноо y, а затем — простейшее неравенство, содержащее
обратную трионометричесую фунцию.
П р и м е р 1. Решить неравенство
arcctg
2
x – 5 arcctg x + 6 > 0.
Р е ш е н и е. Положим arcctg x = y и перепишем исходное
неравенство в виде
y
2
– 5y + 6 > 0;
Неравенство Решение неравенства
arcsin x > a | a | < x Ý (sin a; 1)
arcsin x < a | a | < x Ý (–1; sin a)
arccos x > a (0 < a < π) x Ý (–1; cos a)
arccos x < a (0 < a < π) x Ý (cos a; 1)
arctg x > a | a | < x Ý (tg a; +×)
arctg x < a | a | < x Ý (–×; tg a)
arcctg x > a (0 < a < π) x Ý (–×; ctg a)
arcctg x < a (0 < a < π) x Ý (ctg a; +×)
π
2
---
π
2
---
π
2
---
π
2
---
1
4
---
π
6
---
π
3
---

152 Г л а в а 5. Тригонометрия
15. > 4 sin x + 1.
16. < 0.
17. < 4tg x.
18. 5 + 2 cos 2x m 3 |2 sin x – 1|.
В неоторых случаях при решении неравенств используют
разложение на множители.
П р и м е р 2. Решить неравенство
cos x + cos 2x + cos 3x > 0.
Р е ш е н и е. Преобразуя сумму райних слааемых в про-
изведение, получаем неравенство
cos 2x + 2 cos 2x cos x > 0,
или
cos 2x (2 cos x + 1) > 0.
Последнее неравенство эвивалентно двум системам про-
стейших неравенств:
Объединяя решения этих систем, находим решение исходноо
неравенства.
Ответ.– + 2πn; + 2πn Ÿ + 2πn; + 2πn Ÿ
Ÿ + 2πn; + 2πn , n Ý Z.
Решите неравенство:
19. sin x sin 2x – cos x cos 2x > sin 6x.
20. 2sinx sin 2x sin 3x < sin 4x.
21. sin x sin 3x > sin 5x sin 7x.
22. cos
3
x sin 3x + cos 3x sin
3
x < .
23. sin x l cos 2x.
24. 2tg2x m 3 tg x.
25. sin x < | cos x |.
3sinx 1+
2 sin
2
x sin x 1–+
sin x 1–
----------------------------------------------------
3
cos
2
x
---------------
cos 2x < 0,
cos x < – ;
1
2
---
cos 2x > 0,
cos x > – .
1
2
---
π
4
---
π
4
---
2π
3
------ -
3π
4
------ -
5π
4
------ -
4π
3
------ -
3
8
---
§ 29. Неравенства, содержащие обратные тригоном. функции 153
§ 29. Неравенства, содержащие
обратные тригонометрические функции
Решение простейших неравенств, содержащих обратные три-
онометричесие фунции, приведено в таблице:
Решите неравенство:
1. arcsin x m 5. 2. arcsin x l –2.
3. arccos x m arccos . 4. arccos x > .
5. arctg x > – . 6. arcctg x > 2.
Неравенства вида R(y) > 0, R(y) < 0, де R— неоторая ра-
циональная фунция, а y— одна из обратных трионометри-
чесих фунций (арсинус, аросинус, артаненс, аротан-
енс), решают в два этапа: сначала — неравенство относительно
неизвестноо y, а затем — простейшее неравенство, содержащее
обратную трионометричесую фунцию.
П р и м е р 1. Решить неравенство
arcctg
2
x – 5 arcctg x + 6 > 0.
Р е ш е н и е. Положим arcctg x = y и перепишем исходное
неравенство в виде
y
2
– 5y + 6 > 0;
Неравенство Решение неравенства
arcsin x > a | a | < x Ý (sin a; 1)
arcsin x < a | a | < x Ý (–1; sin a)
arccos x > a (0 < a < π) x Ý (–1; cos a)
arccos x < a (0 < a < π) x Ý (cos a; 1)
arctg x > a | a | < x Ý (tg a; +×)
arctg x < a | a | < x Ý (–×; tg a)
arcctg x > a (0 < a < π) x Ý (–×; ctg a)
arcctg x < a (0 < a < π) x Ý (ctg a; +×)
π
2
---
π
2
---
π
2
---
π
2
---
1
4
---
π
6
---
π
3
---

154 Г л а в а 5. Тригонометрия
решениями последнео неравенства являются y < 2 и y > 3.
Возвращаясь исходному неизвестному, получаем, что данное
неравенство сводится двум простейшим неравенствам
arcctg x < 2 и arcctg x > 3,
имеющим соответственно решения
x
Ý
(ctg 2; +
×
) и
x
Ý
(–
×
; ctg 3).
Объединяя эти решения, находим решение исходноо нера-
венства.
Ответ.(–×; ctg 3) Ÿ (ctg 2; +×).
Решите неравенство:
7. arctg
2
x – 4 arctg x + 3 > 0. 8. log
2
arctg x > 1.
9. + l 2. 10. 4(arccos x)
2
– 1 l 0.
Чтобы решить неравенства, связывающие значения различ-
ных обратных трионометричесих фунций или значения одной
трионометричесой фунции, вычисленные от разных арумен-
тов, удобно вычислить значение неоторой трионометриче-
сой фунции от обеих частей неравенства. Однао следует
учитывать, что полученное при этом неравенство эвивалентно
исходному лишь в том случае, ода множество значений пра-
вой и левой частей исходноо неравенства принадлежит одному
и тому же промежуту монотонности этой трионометричесой
фунции.
П р и м е р 2. Решить неравенство
arcsin x > arccos x.(*)
Р е ш е н и е. Найдем множество допустимых значений x, вхо-
дящих в неравенство: x Ý [–1; 1]. При x < 0 имеем arcsin x < 0,
а arccos x > 0. Следовательно, значения x < 0 не являются ре-
шениями неравенства. При x l 0 а правая, та и левая части
неравенства принимают значения, принадлежащие промежут-
у 0; . Та а на промежуте 0; синус монотонно
возрастает, то при x Ý [0; 1] неравенство (*) эвивалентно нера-
венству
sin (arcsin x) > sin (arccos x) _ x > .
Последнее неравенство при рассматриваемых значениях не-
известноо эвивалентно неравенству
2x
2
> 1. (**)
2
arctgx
2
–arctg x
π
2
---
π
2
---
1 x
2
–
§ 30. Доказательство тригонометрических неравенств 155
Таим образом, решениями исходноо неравенства являются
те решения неравенства (**), оторые принадлежат промежут-
у [0; 1].
Ответ. x Ý ; 1.
Решите неравенство:
11. arccos x > arccos x
2
. 12. arctg x > arcctg x.
13. arcsin x < arcsin (1 – x). 14. tg
2
arcsin x > 1.
§ 30. Доказательство
тригонометрических неравенств
Доазательство неравенств, связывающих значения трионо-
метричесих фунций на всей числовой прямой или на неото-
ром ее промежуте, обычно основано на иcпользовании свойств
фунций: монотонности, ораниченности и т. д.
Пример 1. Доазать, что если α Ý – ; , β Ý – ; ,
то
cos l .
Р е ш е н и е. Для доазательства данноо неравенства до-
статочно представить ео правую часть в виде
= cos cos
и учесть, что если α Ý – ; , β Ý –; , то и Ý
Ý – ; , и следовательно, 0 < cos < 1.
Доажите, что при x Ý 0; выполняется неравенство:
1. sin x cos x m 0,5. 2. sin x + cos x m .
3. tg x + ctg x l 2. 4. tg x l sin x.
5. sin 2x m 2 sin x. 6. m cos.
2
2
-------
π
2
---
π
2
---
π
2
---
π
2
---
αβ+
2
------------- -
cos α cos β+
2
----------------------------------
cos α cos β+
2
----------------------------------
αβ+
2
------------- -
αβ–
2
-------------
π
2
---
π
2
---
π
2
---
π
2
---
αβ–
2
-------------
π
2
---
π
2
---
αβ–
2
-------------
π
2
---
2
cos x 2
x
2
---

154 Г л а в а 5. Тригонометрия
решениями последнео неравенства являются y < 2 и y > 3.
Возвращаясь исходному неизвестному, получаем, что данное
неравенство сводится двум простейшим неравенствам
arcctg x < 2 и arcctg x > 3,
имеющим соответственно решения
x
Ý
(ctg 2; +
×
) и
x
Ý
(–
×
; ctg 3).
Объединяя эти решения, находим решение исходноо нера-
венства.
Ответ.(–×; ctg 3) Ÿ (ctg 2; +×).
Решите неравенство:
7. arctg
2
x – 4 arctg x + 3 > 0. 8. log
2
arctg x > 1.
9. + l 2. 10. 4(arccos x)
2
– 1 l 0.
Чтобы решить неравенства, связывающие значения различ-
ных обратных трионометричесих фунций или значения одной
трионометричесой фунции, вычисленные от разных арумен-
тов, удобно вычислить значение неоторой трионометриче-
сой фунции от обеих частей неравенства. Однао следует
учитывать, что полученное при этом неравенство эвивалентно
исходному лишь в том случае, ода множество значений пра-
вой и левой частей исходноо неравенства принадлежит одному
и тому же промежуту монотонности этой трионометричесой
фунции.
П р и м е р 2. Решить неравенство
arcsin x > arccos x.(*)
Р е ш е н и е. Найдем множество допустимых значений x, вхо-
дящих в неравенство: x Ý [–1; 1]. При x < 0 имеем arcsin x < 0,
а arccos x > 0. Следовательно, значения x < 0 не являются ре-
шениями неравенства. При x l 0 а правая, та и левая части
неравенства принимают значения, принадлежащие промежут-
у 0; . Та а на промежуте 0; синус монотонно
возрастает, то при x Ý [0; 1] неравенство (*) эвивалентно нера-
венству
sin (arcsin x) > sin (arccos x) _ x > .
Последнее неравенство при рассматриваемых значениях не-
известноо эвивалентно неравенству
2x
2
> 1. (**)
2
arctgx
2
–arctg x
π
2
---
π
2
---
1 x
2
–
§ 30. Доказательство тригонометрических неравенств 155
Таим образом, решениями исходноо неравенства являются
те решения неравенства (**), оторые принадлежат промежут-
у [0; 1].
Ответ. x Ý ; 1.
Решите неравенство:
11. arccos x > arccos x
2
. 12. arctg x > arcctg x.
13. arcsin x < arcsin (1 – x). 14. tg
2
arcsin x > 1.
§ 30. Доказательство
тригонометрических неравенств
Доазательство неравенств, связывающих значения трионо-
метричесих фунций на всей числовой прямой или на неото-
ром ее промежуте, обычно основано на иcпользовании свойств
фунций: монотонности, ораниченности и т. д.
Пример 1. Доазать, что если α Ý – ; , β Ý – ; ,
то
cos l .
Р е ш е н и е. Для доазательства данноо неравенства до-
статочно представить ео правую часть в виде
= cos cos
и учесть, что если α Ý – ; , β Ý –; , то и Ý
Ý – ; , и следовательно, 0 < cos < 1.
Доажите, что при x Ý 0; выполняется неравенство:
1. sin x cos x m 0,5. 2. sin x + cos x m .
3. tg x + ctg x l 2. 4. tg x l sin x.
5. sin 2x m 2 sin x. 6. m cos.
2
2
-------
π
2
---
π
2
---
π
2
---
π
2
---
αβ+
2
------------- -
cos α cos β+
2
----------------------------------
cos α cos β+
2
----------------------------------
αβ+
2
------------- -
αβ–
2
-------------
π
2
---
π
2
---
π
2
---
π
2
---
αβ–
2
-------------
π
2
---
π
2
---
αβ–
2
-------------
π
2
---
2
cos x 2
x
2
---
156 Г л а в а 5. Тригонометрия
7. Доажите, что если α Ý [0; π], β Ý [0; π], то
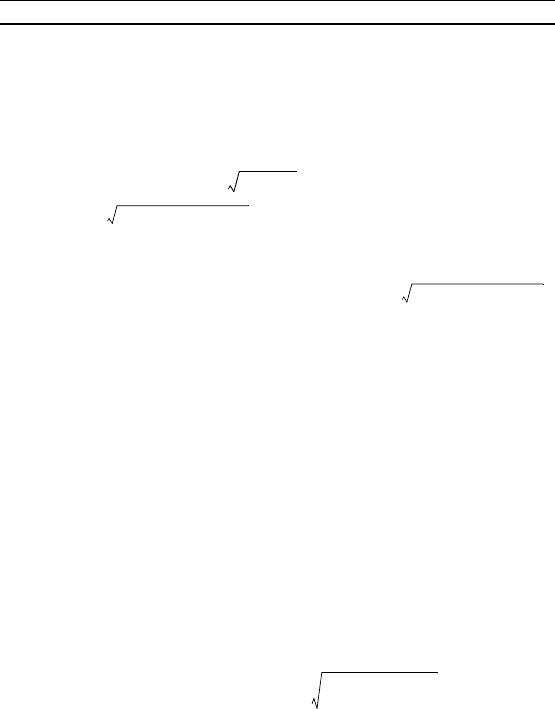
sin l .
Доажите, что при любом действительном x справедливо
соотношение:
8. | a cos x + b sin x | m .
9. m
m a sin
2
x + b sin x cos x + c cos
2
x m
m .
Часто при доазательстве трионометричесих неравенств
используют неравенства, устанавливающие связь между сред-
ним еометричесим и средним арифметичесим двух или не-
сольих положительных чисел.
П р и м е р 2. Доазать, что если α + β + γ = π и α > 0, β > 0,
γ > 0, то
+ + l 6. (*)
Решение. Та а sin , sin , sin неотрицательны,
то, используя неравенство, связывающее среднее арифметиче-
сое трех чисел и их среднее еометричесое, имеем
+ + l . (**)
Преобразуем подоренное выражение:
sin sin sin = sin cos – cos .
Учитывая, что α + β + γ = π, получим
cos = cos – = sin , cos < 1,
и, значит,
sin sin sin m sin 1 – sin .
αβ+
2
------------- -
sin α sin β+
2
---------------------------------
a
2
b
2
+
ac a
2
b
2
c
2
2ac–++–+
2
------------------------------------------------------------------------- -
ac a
2
b
2
c
2
2ac–++++
2
--------------------------------------------------------------------------
1
sin
α
2
---
-------------
1
sin
β
2
---
-------------
1
sin
γ
2
---
-------------
α
2
---
β
2
---
γ
2
---
1
sin
α
2
---
-------------
1
sin
β
2
---
-------------
1
sin
γ
2
---
-------------
3
sin
α
2
--- sin
β
2
--- sin
γ
2
---
3
------------------------------------------------
α
2
---
β
2
---
γ
2
---
1
2
---
α
2
---
βγ–
2
------------
βγ+
2
------------
βγ+
2
------------
π
2
---
α
2
---
α
2
---
βγ–
2
------------
α
2
---
β
2
---
γ
2
---
1
2
---
α
2
---
α
2
---
§ 30. Доказательство тригонометрических неравенств 157
Положим y = sin и рассмотрим фунцию f(y) = y(1 – y),
входящую в правую часть последнео неравенства. Наибольшее
значение этой фунции на промежуте [0; 1] равно . Поэтому
sin sin sin m .
Из этоо неравенства следует, что
l 6. (***)
Наонец, из неравенств (**) и (***) вытеает справедливость
исходноо неравенства.
10. Доажите, что если α + β + γ = π и α > 0, β > 0, γ > 0, то
(1 – cos α)(1 – cosβ)(1 – cosγ) m .
11. Доажите, что если α + β + γ = π и α Ý 0; , β Ý 0; ,
γ Ý 0; , то
+ + l 6.
12. Доажите, что если α + β + γ = π и α Ý 0; , β Ý 0; ,
γ Ý 0; , то
tg
2
α + tg
2
β + tg
2
γ l 9.
13. Доажите, что если α + β + γ = π, то
cos cos cos m .
14. Доажите, что если α + β + γ = π, то
sin
2
+ sin
2
+ sin
2
l .
15. Доажите, что если α + β + γ = π, то
cos α + cos β + cos γ m .
α
2
---
1
2
---
1
4
---
α
2
---
β
2
---
γ
2
---
1
8
---
3
sin
α
2
--- sin
β
2
--- sin
γ
2
---
3
------------------------------------------------
1
8
---
π
2
---
π
2
---
π
2
---
1
cos α
-------------
1
cos β
-------------
1
cos γ
------------
π
2
---
π
2
---
π
2
---
α
2
---
β
2
---
γ
2
---
3
8
---
3
α
2
---
β
2
---
γ
2
---
3
4
---
3
2
---

156 Г л а в а 5. Тригонометрия
7. Доажите, что если α Ý [0; π], β Ý [0; π], то
sin l .
Доажите, что при любом действительном x справедливо
соотношение:
8. | a cos x + b sin x | m .
9. m
m a sin
2
x + b sin x cos x + c cos
2
x m
m .
Часто при доазательстве трионометричесих неравенств
используют неравенства, устанавливающие связь между сред-
ним еометричесим и средним арифметичесим двух или не-
сольих положительных чисел.
П р и м е р 2. Доазать, что если α + β + γ = π и α > 0, β > 0,
γ > 0, то
+ + l 6. (*)
Решение. Та а sin , sin , sin неотрицательны,
то, используя неравенство, связывающее среднее арифметиче-
сое трех чисел и их среднее еометричесое, имеем
+ + l . (**)
Преобразуем подоренное выражение:
sin sin sin = sin cos – cos .
Учитывая, что α + β + γ = π, получим
cos = cos – = sin , cos < 1,
и, значит,
sin sin sin m sin 1 – sin .
αβ+
2
------------- -
sin α sin β+
2
---------------------------------
a
2
b
2
+
ac a
2
b
2
c
2
2ac–++–+
2
------------------------------------------------------------------------- -
ac a
2
b
2
c
2
2ac–++++
2
--------------------------------------------------------------------------
1
sin
α
2
---
-------------
1
sin
β
2
---
-------------
1
sin
γ
2
---
-------------
α
2
---
β
2
---
γ
2
---
1
sin
α
2
---
-------------
1
sin
β
2
---
-------------
1
sin
γ
2
---
-------------
3
sin
α
2
--- sin
β
2
--- sin
γ
2
---
3
------------------------------------------------
α
2
---
β
2
---
γ
2
---
1
2
---
α
2
---
βγ–
2
------------
βγ+
2
------------
βγ+
2
------------
π
2
---
α
2
---
α
2
---
βγ–
2
------------
α
2
---
β
2
---
γ
2
---
1
2
---
α
2
---
α
2
---
§ 30. Доказательство тригонометрических неравенств 157
Положим y = sin и рассмотрим фунцию f(y) = y(1 – y),
входящую в правую часть последнео неравенства. Наибольшее
значение этой фунции на промежуте [0; 1] равно . Поэтому
sin sin sin m .
Из этоо неравенства следует, что
l 6. (***)
Наонец, из неравенств (**) и (***) вытеает справедливость
исходноо неравенства.
10. Доажите, что если α + β + γ = π и α > 0, β > 0, γ > 0, то
(1 – cos α)(1 – cosβ)(1 – cosγ) m .
11. Доажите, что если α + β + γ = π и α Ý 0; , β Ý 0; ,
γ Ý 0; , то
+ + l 6.
12. Доажите, что если α + β + γ = π и α Ý 0; , β Ý 0; ,
γ Ý 0; , то
tg
2
α + tg
2
β + tg
2
γ l 9.
13. Доажите, что если α + β + γ = π, то
cos cos cos m .
14. Доажите, что если α + β + γ = π, то
sin
2
+ sin
2
+ sin
2
l .
15. Доажите, что если α + β + γ = π, то
cos α + cos β + cos γ m .
α
2
---
1
2
---
1
4
---
α
2
---
β
2
---
γ
2
---
1
8
---
3
sin
α
2
--- sin
β
2
--- sin
γ
2
---
3
------------------------------------------------
1
8
---
π
2
---
π
2
---
π
2
---
1
cos α
-------------
1
cos β
-------------
1
cos γ
------------
π
2
---
π
2
---
π
2
---
α
2
---
β
2
---
γ
2
---
3
8
---
3
α
2
---
β
2
---
γ
2
---
3
4
---
3
2
---

158 Г л а в а 5. Тригонометрия
В примере 2 требовалось найти наибольшее значение фун-
ции sin 1 – sin . Выполнив замену переменной, мы по-
лучили, что исомое значение совпадает с наибольшим значе-
нием фунции f(y) = y(1 – y) на промежуте [0; 1]. Аналоич-
ный прием часто используют в тех случаях, ода требуется
найти множества значений неоторых трионометричесих вы-
ражений.
16. Доажите, что –4 m cos 2x + 3 sin x m 2 .
17. Доажите, что cos
3
x + cos
6
x m .
18. Доажите, что если | p | < 2, то
sin
2
x + p sin x + q l .
19. Доажите, что sin
2
x cos
2
x m .
Доазательство неравенств, связывающих трионометриче-
сие фунции и неоторые мноочлены, заданные на опреде-
ленных интервалах изменения арументов, проводят с помощью
омбинации рассмотренных выше приемов. При этом в процес-
се доазательства часто используют двойное неравенство
sin x m x m tg x,(1)
справедливое при всех x Ý 0; .
П р и м е р 3. Доазать, что на промежуте (0; π) имеет
место неравенство
x – < sin x.
Р е ш е н и е. Представим фунцию sin x в виде
sin x = 2 tg cos
2
= 2 tg 1 – sin
2
.
Используя двойное неравенство (1), имеем
tg l ,1 – sin
2
l 1 – .
1
2
---
α
2
---
α
2
---
1
2
---
1
8
---
1
4
---
p
2
–4q–
4
------------------------ -
1
4
---
π
2
---
x
3
4
------
x
2
---
x
2
---
x
2
---
x
2
---
x
2
---
x
2
---
x
2
---
x
2
4
------
§ 30. Доказательство тригонометрических неравенств 159
Применяя полученные оцени правой части исходноо нера-
венства, убеждаемся в ео справедливости.
20. Доажите, что на промежуте (0; π) справедливо нера-
венство
cos x < 1 – + .
21. Доажите, что на промежуте 0; справедливо нера-
венство
x – < tg x.
22. Доажите, что 1 – cos x m .
x
2
2
------
x
4
16
------
π
2
---
x
3
2
------
x
2
2
------

158 Г л а в а 5. Тригонометрия
В примере 2 требовалось найти наибольшее значение фун-
ции sin 1 – sin . Выполнив замену переменной, мы по-
лучили, что исомое значение совпадает с наибольшим значе-
нием фунции f(y) = y(1 – y) на промежуте [0; 1]. Аналоич-
ный прием часто используют в тех случаях, ода требуется
найти множества значений неоторых трионометричесих вы-
ражений.
16. Доажите, что –4 m cos 2x + 3 sin x m 2 .
17. Доажите, что cos
3
x + cos
6
x m .
18. Доажите, что если | p | < 2, то
sin
2
x + p sin x + q l .
19. Доажите, что sin
2
x cos
2
x m .
Доазательство неравенств, связывающих трионометриче-
сие фунции и неоторые мноочлены, заданные на опреде-
ленных интервалах изменения арументов, проводят с помощью
омбинации рассмотренных выше приемов. При этом в процес-
се доазательства часто используют двойное неравенство
sin x m x m tg x,(1)
справедливое при всех x Ý 0; .
П р и м е р 3. Доазать, что на промежуте (0; π) имеет
место неравенство
x – < sin x.
Р е ш е н и е. Представим фунцию sin x в виде
sin x = 2 tg cos
2
= 2 tg 1 – sin
2
.
Используя двойное неравенство (1), имеем
tg l ,1 – sin
2
l 1 – .
1
2
---
α
2
---
α
2
---
1
2
---
1
8
---
1
4
---
p
2
–4q–
4
------------------------ -
1
4
---
π
2
---
x
3
4
------
x
2
---
x
2
---
x
2
---
x
2
---
x
2
---
x
2
---
x
2
---
x
2
4
------
§ 30. Доказательство тригонометрических неравенств 159
Применяя полученные оцени правой части исходноо нера-
венства, убеждаемся в ео справедливости.
20. Доажите, что на промежуте (0; π) справедливо нера-
венство
cos x < 1 – + .
21. Доажите, что на промежуте 0; справедливо нера-
венство
x – < tg x.
22. Доажите, что 1 – cos x m .
x
2
2
------
x
4
16
------
π
2
---
x
3
2
------
x
2
2
------
