Crank J. Free and Moving Boundary Problems
Подождите немного. Документ загружается.


282
Fixed-domain methods
by Budak and Gapenko (1971) for the one-dimensional case and ex-
tended
to
the
multi-dimensional problem by Niezgodka and Pawlow
(1983).
Brezis (1970) and Lions (1969) used monotonicity methods in their
analyses and this approach was later developed by Jerome (1976, 1977)
and Damlamian (1977, 1979).
Duvaut (1975) extended the variational-inequality analysis
to
two-
phase problems
and
Fremond (1974) used the same approach indepen-
dently. Various later papers are quoted by N,iezgOdka (1983) and
by
Pawlow (1981).
The
latter paper, together with those of Jerome (1977)
and Budak and
Gapenko
(1971), considered domains having only
piecewise-regular boundaries.
For
problems in
one
space dimension, references are given by
Niezgodka (1983) to papers
on
regularity
and
global continuity of weak
solutions. Very general forms of non-linear conditions
on
the
free bound-
ary were examined by Fasano and Primicerio
(1979a), Fasano (1980) and
NiezgOdka (1979), and in several papers in Russian. Papers by Fasano
(1980) and Fasano
and
Primicerio (1979b, 1981) deal with Cauchy-type
conditions
on
the
free boundary and with critical cases for which solutions
are non-existent.
Other
related papers by Meirmanov (1981a,b) and
Pukhnachev (1980)
are
mentioned. Curvature of
the
free boundary was
studied by Fasano
and
Primicerio (1979c), 'Friedman
and
Jensen (1977),
and Primicerio (1980). A
paper
by Shishkin (1975) considered problems
with a discontinuous free boundary.
Other
sections
of
Niezg6dka's (1983) survey refer to degenerate
problems, e.g. with zero specific heat, and
to
global non-linearities,
concentrated capacities, time and spatial periodicities, hysteresis,
and
non-parabolic Stefan-like problems. Finally, fundamental difficulties as-
sociated with the accurate tracking of a free boundary are mentioned.
Sufficient global regularity is provided only by results for the one-
dimensional problems (Wilson
et al. 1978; Primicerio 1981a) and multi-
dimensional single-phase problems (Wilson
et al. 1978; Friedman 1975).
Damlamian (1977, 1979) produced general results
on
the
regularity of
weak solutions but they
do
not
help
to
determine
the
movement of
the
free
boundary.

7.
Analytical solution of seepage
problems
7.1. Introduction
THE
practical importance
of
free-boundary problems
in
porous flow has
stimulated
many
attempts
to
find analytical solutions, both approximate
and
exact.
The
latter
depend
almost entirely on finding suitable conformal
mappings
of
the
flow region in
the
physical plane
on
to
both
the
hodograph plane
and
the
flow-potential plane. A comprehensive account
of
many ingenious transformations
is
given by Polubarinova-Kochina
(1962).
Other
basic texts
are
by
Bear
(1972)
and
Harr
(1962).
In
this
chapter
the
most commonly used mappings
and
the
ways in which they
are applied
to
selected problems are described.
7.2. Approximate methods
7.2.1. Dupuit's approximation
Dupuit (1863) made
the
simplifying assumption
that
the
slope
of
the
free surface in unconfined flow is very small. This seems
to
be
substan-
tiated by observations
of
most ground-water flows. In steady two-
dimensional flow without accretion
in
the
vertical
x-z
plane,
the
free
surface is a streamline
and
at
every point
on
it
the
rate
of
flow
per
unit
area q. is given by Darcy's law
to
be
q. =
-K
dcb/ds =
-K
dz/ds
=
-K
dhlds,
(7.1)
where s is measured along
the
streamline, since
cb
= z = h
on
the
free
boundary.
Dupuit
replaced dhlds by
dhldx
for small gradients, which
is
equivalent
to
assuming
that
the
equipotential surfaces are vertical, i.e.
cb
= cb(x) independent
of
z,
and
the
flow
is
assumed
to
be
horizontal. Thus
we now consider a uniform one-dimensional flow based
on
the
expression
q"
= -
K"
dhldx,
h
=
h(x),
(7.2)
and
we should examine
the
error
introduced by neglecting
the
vertical
flow
qz
=-K
z
acblaz.

284
Analytical solution
of
seepage problems
The
exact expression for
the
total horizontal discharge through
the
medium,
Q,
is
I
h
(X)
acf>
a
{l
h
(X)
}
Q = -
K,.,
ax
(x, z)
dz
= -
Kx
oX
cf>(x,
z)
dz
-!h
2
= -
K,.,
acf>'
lax,
(7.3)
where
h~
=
cf>(x,
z) dz.
I
h
(X)
By Dupuit's assumption we get
Q = -
K,.,h
ahldx = -
K,.,
aGh
2)/ax,
(7.4)
i.e.
cf>'
has been replaced by
!h
2
. Integration by parts of
the
expression for
cf>'
in (7.3) gives
I
h
(X)
Ih(X)
cf>'
=
cf>(x,
z)
dz
-!h
2
=
(zcf»~(x)
-
z(acf>laz)
dz
-!h
2
(x)
=!h
2
(x){
1 +
K,.,~(X)
r(X)
zqAx, z)
dZ},
(7.5)
where
qz
=-K.:
acf>laz,
qz(h)<O.
The
integral
tenn
in (7.5) measures
the
error
introduced
by
replacing
cf>'
by!h
2
. Since
on
the
free surface
cf>
=
h,
qzl(Jx
=dhldx, and
dcf>ldx
=dhldx
= -(lJxIK,.,)-(qz/K,.,) dhldx, with
(Jx,
4
evaluated
at
z =
h,
we
see
that
-
K,.,
(dhldx)2
qz
= 1 + (KJK.:)(dhldx)2'
z=h.
The
range in
the
error
tenn
can
be
expressed as
!h2-
cf>'
(K,.,IK.:)/(dh/dx)2
0<
!h2 <1+(K,.,IK,.,)(dhldx)2.
(7.6)
As
an example, we apply Dupuit's fonnula (7.4)
to
the
problem of
the
simple dam of width L separating two reservoirs with water heights
ho
and
hL
(Fig. 2.1 with
Xl
=
L,
Yl
=
ho,
Y2
= h
L
).
Integrating
the
second
eqn
(7.4) we obtain, noting that Q
is
constant throughout
the
dam for steady
flow and with
K,.,
= K for an isotropic homogeneous dam,
Q =
K(h~-
hD/(2L).
(7.7)
The
correct expression for Q (i.e. without making
the
Dupuit assump-
tions) follows by integrating (7.3) and inserting
cf>
= h(x) =
ho
at
x = 0
to
obtain (Charni, 1951)
I
h
(X)
(QIK)x
= -
cf>(x,
z)
dz
+i(h
2
+
h~).
(7.8)

Approximate methods
285
But at
x=L
we have
q,(L,z)=h
L
,
O<z~hL>
and
q,=z,
hL~Z~hs,
where hs is
the
height of the separation point. Hence
at
x = L, using
(7.8),
(Q/K)L
=-l"'-h
L
dZ_(s
Z dz
+!(h~+h~)=!(h~-hD,
and
so
the
Dupuit
formula (7.7) for
the
total discharge Q turns
out
to
be
exact in this case.
On
the
other
hand,
the
first of (7.7) approximates
the
free surlace by a
parabola which passes through
h =
ho
at
x = 0
and
h =
hL
at
x =
L.
Thus
the
Dupuit solution does
not
include a seepage surlace and the parabolic
free surlace meets
both
the
inlet
and
outlet faces of
the
dam
at
finite
angles given
by
dh/dx
=
-Q/(Kh
o
),
x=O;
dh/dx
=
-Q(Khd,
x=L.
Further discussion of
the
paradoxes associated with
the
Dupuit assump-
tions is
to
be
found in
Bear
(1972). A rough guideline proposed for
practical purposes is
that
the
Dupuit formulae are acceptable
if
the
definitive lengths in
the
direction of flow are greater than twice
the
depth
of
the flow region.
It
can similarly
be
shown (Polubarinova-Kochina 1962)
that
the
Dupuit
expression for radial flow
to
a fully penetrating well of radius
rw
in which
h = hw is also exact
and
given by
Q 1TK(hi.-
h~)
(7.9)
1n(rw/
R
) ,
where
h =
hR
at
r = R.
Other
examples of Dupuit formulae are given by
Bear
(1972) jncluding cases
of
horizontally and vertically stratified media
for which Outmans (1964) produced generalized formulae.
7.2.2. Boussinesq's equations
Dupuit's approximations can
be
combined with a continuity equation of
flow averaged in
the
usual way over
the
vertical coordinate z in
order
to
reduce a three-dimensional free-boundary problem
to
two dimensions.
As
an example we can consider an element of volume
of
the
flow region
bounded below by a horizontal impervious base, above by the
fEee
surlace and with vertical sides
at
x±8x/2
and
y±8y/2.
H q is taken
to
be
the
flow
rate
per
unit width in
the
y-direction but over
the
whole depth of
the
element
h(x,
y,
t),
then
in the limit the appropriate conservation
expression can
be
written
a a
ah
--(q,.)--(q
)+N=n-.
ax
ay Y
at

286 Analytical solution
of
seepage problems
Here
n is an effective porosity, N(x,
y,
t) allows for accretion in
the
z -direction
on
the
free surface, and any contribution associated
With
the
increase of pressure in
the
element due
to
the
change in height of
the
free
surface is neglected. Introduction of Dupuit's approximations for
<Ix,
qy
in
an
isotropic medium gives
!~
(Ka(h)2)+!~
(Ka(h)2)+N=n
ah,
2ax
ax
2ay
ay at
(7.10)
which is known as Boussinesq's equation for unsteady porous flow with
accretion
on
the
free boundary.
The
steady-state form of (7.10), referred
to
as Forchheimer's equation, is linear in h
2
•
The
usual special forms
follow for a homogeneous medium
(K
= constant)
and
in
the
steady state
without accretion we have
a
2
(h)2 a
2
(h)2
--+--=0
ax
2
ay2 .
Suitable amendments are needed for an anisotropic medium, when
K
x
1=Ky·
A simple extension includes a slightly sloping impervious base with
height
'I'J
=
'I'J(x,
y).
Then
(7.10)
Can
be
written as
a a ah
-{K(h-'l'J)
ah/ax}+-{K(h-'l'J)
ah/ay}+N=
n-,
(7.11a)
ax ay
at
or, putting b(x,
y,
t)=
h(x,
y,
t)-'l'J(x, y), as
~
(b
ab)+~
(b
ab)+~
(b
a'I'J)
+~
(b
a'I'J)+
N =!!. ab, (7. 11 b)
ax ax ay ay ax ax ay ay K K at
if
the
medium is homogeneous.
If
a'I'J/ax,
a'I'J/ay
are constant, i.e.
the
base
is plane, a change of variables
to
,
Kta'I'J
x
=x+--
n
ax'
reduces (7.11b)
to
,
Kta'I'J
y
=y+--,
n ay
t'=
t,
a (b
ab)
a
(b
ab)
N n
ab
ax' ax' + ay' ay' + K = Kat"
(7.11c)
which has
the
same form as (7.10) and is sometimes also attributed
to
Forchheimer.
Bear
(1972) presented some simple exact solutions of Forchheimer's
equations
and
also for Boussinesq's equation for ground-water flows of
practical interest.
There
are references
to
other
results
but
they are
limited in number
bec~use
of the non-linearity of eqn (7.10). Various

Approximate methods
287
linearization techniques have
been
applied (Bear 1972).
The
first is based
on
the
assumption
that
the
height
of
the
free surface above
the
horizontal
base varies only slightly so that
h =
Ii
+ h' where
h'«
h and
Ii
is the
average height.
Equation
(7.10) becomes
Kh{iJ
2
h'liJx
2
+iPh'liJy2}+N=
n
iJh'liJt,
(7. lOa)
which is linear in
h'
and
some solutions can
be
obtained
by
recognizing
(7.10a) as being
related
to
the
heat-flow
or
diffusion equation.
Bear
(1972) gave a
number
of
examples
and
references.
In
the
second method
(7.10)
is rewritten as
!(iJ
2
(h)2
+
iJ
2
(h)2)
+ N
=~
iJ(h)2
2
iJx
2
iJy2
K 2Kh
iJt
(7.10b)
and
variations in h
are
considered
to
be
such
that
Khln
is assumed
constant,
equal
to
Khln. Alternatively (7.10b) is written
2
Kh
a
=-.
n
(7.10c)
Chami
(1951)
wrote
Boussinesq's equation for one-dimensional flow as
KduiJ
2
u
iJu
-;;:
df
iJx
2
= iJt' (7.10d)
where
u = J[(h) dh,
and
chose
du/df=
11A = constant. Thus (7.10d) is a
linear diffusion
equation
and
dflf=A
dh
so
that
f=B
exp(Ah).
The
constants A
and
B
are
chosen
so
that
f=
h at
the
boundaries.
7.2.3. Other approximate methods
Bear
(1972)
referred
to
early work
by
Lembke
(1887),
Weber
(1928),
Polubarinova-Kochina (1962),
and
Aravin and Numerov (1965)
based
on
a quasi-steady-state method.
The
free boundary is assumed always
to
have
the
shape
of
the
Dupuit
steady-state approximation for
the
bound-
ary conditions, e.g. reservoir level, pertaining at any given time;
the
time-dependent flow
pattern
is approximated
by
a succession
of
steady
states.
Bear
(1972) gave details
of
the
unsteady solution
of
Aravin and
Numerov (1965) for one-dimensional flow
to
a ditch.
Instead
of
reducing
the
dimension
of
the
equation
of
flow by
Dupuit's
assumptions,
the
standard
method
of small perturbations can
be
applied
to
the
full set
of
equations
and
boundary conditions, i.e.
cf>(x,
y,
Z,
t) can
be
determined such
that
V
2
cf>
= 0 in
the
flow region,
and
the
free surface
boundary condition,
iJcf>
[(iJcf»2
(iJcf»2
(iJcf»2]
iJcf>
n-=K
- + - + -
-(K+N)-+N
iJt
iJx
iJy
iJz iJz
is satisfied
together
with appropriate conditions
on
the
fixed boundaries.

288
Analytical solution
of
seepage problems
Bear
(1972) presented details based
on
the
work of Polubarinova-
Kochina (1962)
and
others who also discussed a shallow-flow approxima-
tion which is similar
to
the
perturbation approach.
7.3. Hodograph method: confonnal transformations
The
discussion in this section will
be
confined
to
porous flow in
homogeneous isotropic media and so we shall define a flow vector q
related
to
a flow potential,
«>,
by
q
=
-grad
4>.
(7.11)
The
vector q is
the
volume flow
per
unit area and in two-dimensional flow
q has components
<Ix,
qy
in
the
x, y directions, where
qx
=
-CJ«>ICJx,
qy
=
-CJ«>ICJy
(7.12)
and in any general direction
s,
q. =
-CJ«>ICJs.
7.3.1. Hodograph plane
Figure 7.1a shows any curve r in
the
physical plane x, y in which
two-dimensional flow is occurring. A flow vector q with components
<Ix,
qy
exists
at
each point of r and so in a second plane with cartesian axes
<Ix,
qy
we can generate a curve
f'
(Fig. 7.1b) from
the
end
points of
the
vectors q
for all points
on
r. This curve
f'
is called
the
hodograph representation of
r and
f'
is
a mapping
of
the
curve r in
the
x, y plane
on
to
the
hodograph
plane
<Ix,
qy.
Strictly,
the
term
hodograph refers
to
velocities
but
the
volume flow is a
more
satisfactory concept in
the
present context
and
q
can clearly
be
interpreted as a suitably defined velocity.
In
the
various problems formulated in
Chapter
2, conditions along
straight
or
curved boundary lines were expressed in terms of flow
poten-
tials
«>
or
their derivatives expressing rates
of
flow across
the
surfaces.
Thus it is possible
to
map
the
various boundary segments
on
to
the
hodograph plane. Intersections of boundaries in
the
x,
y plane map into
intersections in
the
hodograph plane,
but
in general it is
not
possible
to
y
(b)
B'
o
FIG. 7.1. Hodograph mapping
Hodograph method: conformal transformations
289
associate individual points in the one plane with particular points in the
other plane. Fortunately, this
is
not necessary in the present context but
we shall confine attention to cases of one-to-one correspondence between
the
two planes. The extension to a hodograph space with a cartesian
coordinate system
q,."
qy,
q%
presents no difficulties (Bear, Zaslavsky, and
Innay, 1968).
The
hodograph representation of
the
following boundary
conditions are frequently required.
We
take the
x,
y plane to
be
vertical
with
y measured vertically upwards.
(i)
Imperoious boundary. This boundary is a streamline and we know that
qy
=
q,.,
tan
(3,
where
(3
is
the angle between the x-axis and the tangent to
the streamline.
In
general,
(3
varies from point
to
point along a curved
boundary
and
so
do
q,."
qy
in an unknown
way
so that the hodograph
mapping
is
not
possible. However, it is clear that for a straight-line
impervious boundary the hodograph is a parallel straight line passing
through
the
origin of the hodograph plane (Fig.7.2a,b).
y
(a)
(b)
o
x
FIG. 7.2. Plane impervious boundary
(ii) Equipotential boundary.
Here
the
flow
is
normal
to
the boundary and
so
qy
=
q,.,
cot
(3
=
q,.,
tan
((3
-1T/2). Thus
the
hodograph line of a straight-
line equipotential boundary making an angle
(3
with
the
+x-axis
is
a
straight line through the origin making an angle
(3
-1T/2 with
the
q,.,
axis,
i.e. normal to
the
boundary in the physical plane (Fig. 7.3a,b).
y
(a)
(b)
x
FIG. 7.3. Plane equipotential boundary
290
Analytical solution
of
seepage problems
y
(a) (b)
x
(0,-1)
FIG. 7.4. Plane seepage face
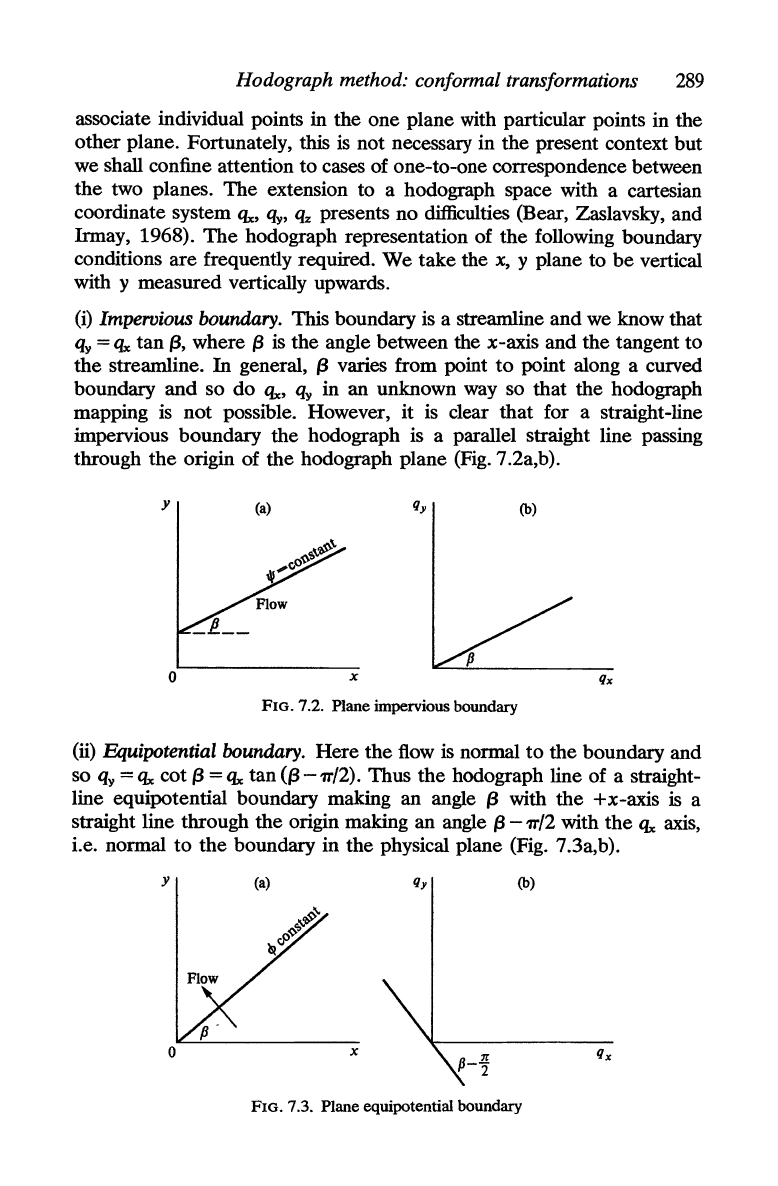
(iii)
Seepage
face.
For points along a straight seepage face as in Fig. 7 Aa,
since
q,
= y we have
oq,/os
=
-tlx
cos
{3
+
qy
sin
{3
=
oy/os
=
-sin
(3,
i.e.
qy
=
tlx
tan({3
-
'7T/2)
-1,
and
the
hodograph of
the
straight seepage face is a
straight line
at
an angle
{3
-
'7T/2
with the tlx
axis
and passing through
the
point (0,
-1),
i.e. perpendicular
to
the physical seepage face (Fig. 7.4b).
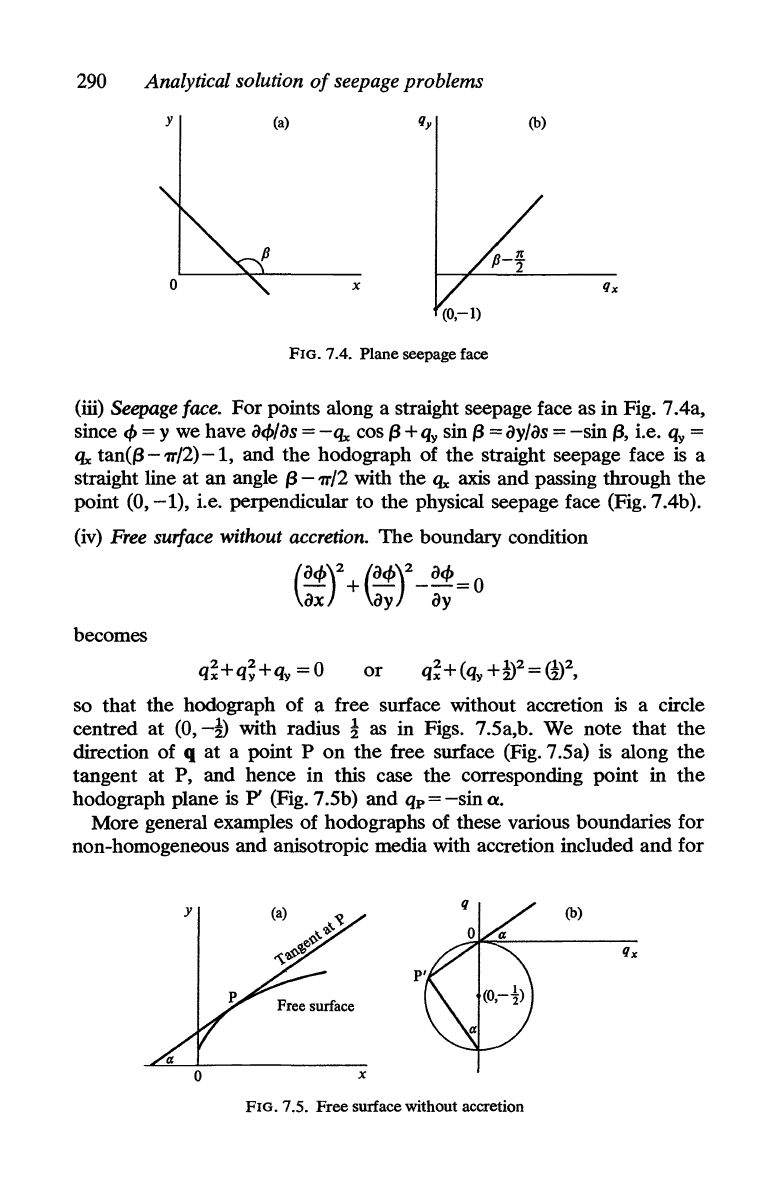
(iv)
Free
surface
without
accretion.
The
boundary condition
(
Oq,)2
+
(oq,)2
_
oq,
= 0
oX
oy oy
becomes
or
so that the hodograph of a free surface without accretion is a circle
centred
at
(0, -!) with radius !
as
in Figs. 7.Sa,b. We note
that
the
direction of q
at
a point P
on
the
free surface (Fig. 7.Sa)
is
along
the
tangent at P, and hence in this case the corresponding point in
the
hodograph plane
is
P'
(Fig. 7 .Sb) and qp =
-sin
a.
More general examples of hodographs of these various boundaries for
non-homogeneous and anisotropic media with accretion included
and
for
(b)
FIG. 7.5.
Free
surface without accretion
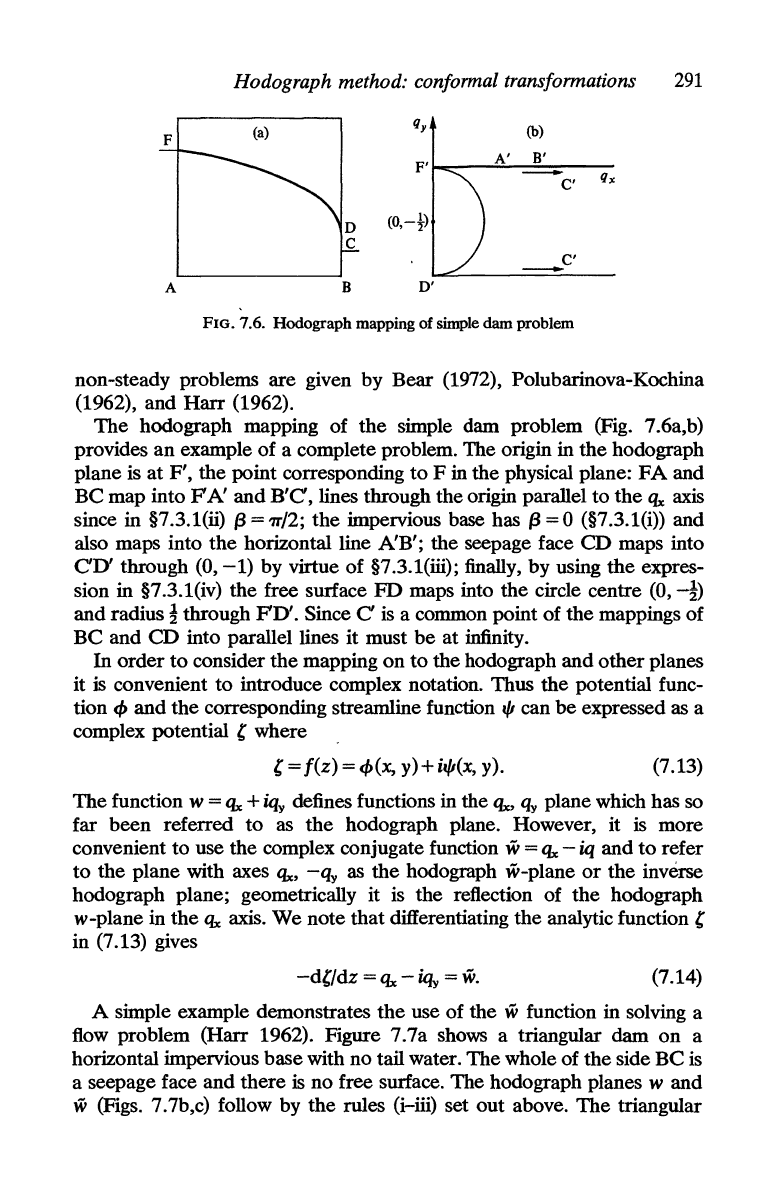
Hodograph method: conformal transformations
291
(a)
qy
(b)
F
F'
A'
B'
-
C'
q",
D
(O,-i)
C
C'
-
A B
D'
FIG. 7.6. Hodograph mapping of simple dam problem
non-steady problems are given by Bear (1972), Polubarinova-Kochina
(1962), and
Harr
(1962).
The
hodograph mapping of
the
simple dam problem (Fig. 7.6a,b)
provides an example of a complete problem. The origin in the hodograph
plane is
at
F', the point corresponding
to
F in the physical plane:
FA
and
Be
map into
FA!
and
B'C,
lines through the origin parallel to
the
tIx
axis
since in §7.3.1(ii) (3=7r/2;
the
impervious base has
(3=0
(§7.3.1(i» and
also maps into
the
horizontal line A!B'; the seepage face CD maps into
CD'
through (0,
-1)
by virtue of §7.3.1(iii); finally, by using
the
expres-
sion in §7.3.1(iv) the
free surface
FD
maps into the circle centre (0,
-!)
and
radius!
through
FD'.
Since C
is
a common point of the mappings of
Be
and CD into parallel lines it must be
at
infinity.
In order
to
consider
the
mapping on
to
the hodograph and other planes
it
is
convenient to introduce complex notation. Thus the potential func-
tion
q,
and
the
corresponding streamline function
1/1
can
be
expressed as a
complex potential , where
,=
f(z)
= q,(x, y) +
il/l(x,
y).
(7.13)
The function
w =
tIx
+
iqy
defines functions in the
tIx,
qy
plane which has so
far been referred to as
the
hodograph plane. However, it
is
more
convenient to use the complex conjugate function w =
tIx
- iq and
to
refer
to
the plane with axes
tIx,
-qy
as
the hodograph w-plane
or
the inverse
hodograph plane; geometrically it is the reflection of
the
hodograph
w-plane in
the
tIx
axis.
We
note that differentiating
the
analytic
function'
in (7.13) gives
-d'/dz
=tIx-ilh
=
w.
(7.14)
A simple example demonstrates
the
use of the w function in solving a
flow
problem (Harr 1962). Figure 7.7a shows a triangular
dam
on
a
horizontal impervious base with no tail water.
The
whole of the side
Be
is
a seepage face and there
is
no free surface. The hodograph planes w and
w (Figs. 7.7b,c) follow by
the
rules
(i-iii)
set
out
above.
The
triangular
