Crank J. Free and Moving Boundary Problems

2 Moving-boundary problems: formulation

somewhat indiscriminately,

to

Stefan's publications. Stefan (1889a) de-

rived

the

large latent-heat approximation given in eqn (3.158).

In

his

paper

(1889b)

he

extended this solution

to

include a time-dependent

surface temperature. Stefan

(1889b) also quoted the error-function type

of solution discussed in §3.2 for

the

single-phase problem, and derived

the

associated subsidiary equations (3.14) and (3.15), together with a

further second-order approximation of (3.14).

In

the

same paper, Stefan

also pointed out that

if

a semi-infinite liquid solidifies in such a way that

the

solidification boundary proceeds at a constant rate,

the

temperature,

u,

can

be

expressed in the form

u =

A(e

at

-

mX

-1)/a,

where A,

a,.

and m are constants, and

the

velocity xlt of solidification is

aIm.

The

full solution

is

quoted in eqn (3.183). Finally, Stefan (1889b)

developed a general solution in

the

form of two Taylor series.

The

whole

of this paper published in 1889 is reproduced in Stefan (1891).

Surveys of

the

early literature with numerous references dating from

the

time of Stefan have been written by Bankoff (1964), Muehlbauer and

Sunderland (1965), and Boley (1972). Rubinstein's classic book (1971)

gives a

systemat~

presentation of

the

mathematical developments in

Stefan problems

up

to that time. More recent surveys are given by

Furzeland

(1977a), Hoffman (1977), Fox (1979), and Crank (1981), all

with useful bibliographies. Reports

on

several conferences (Ockendon

and Hodgkins 1975; Wilson, Solomon, and Boggs 1978; Furzeland

1979a; Magenes 1980; Albrecht, Collatz, and Hoffman 1980; Fasano

and Premicerio 1983) contain up-to-date accounts of mathematical de-

velopments and of wide-ranging applications to problems in physical and

biological sciences, engineering, metallurgy, soil mechanics, decision and

control theory, etc. which are of practical importance in sundry industries.

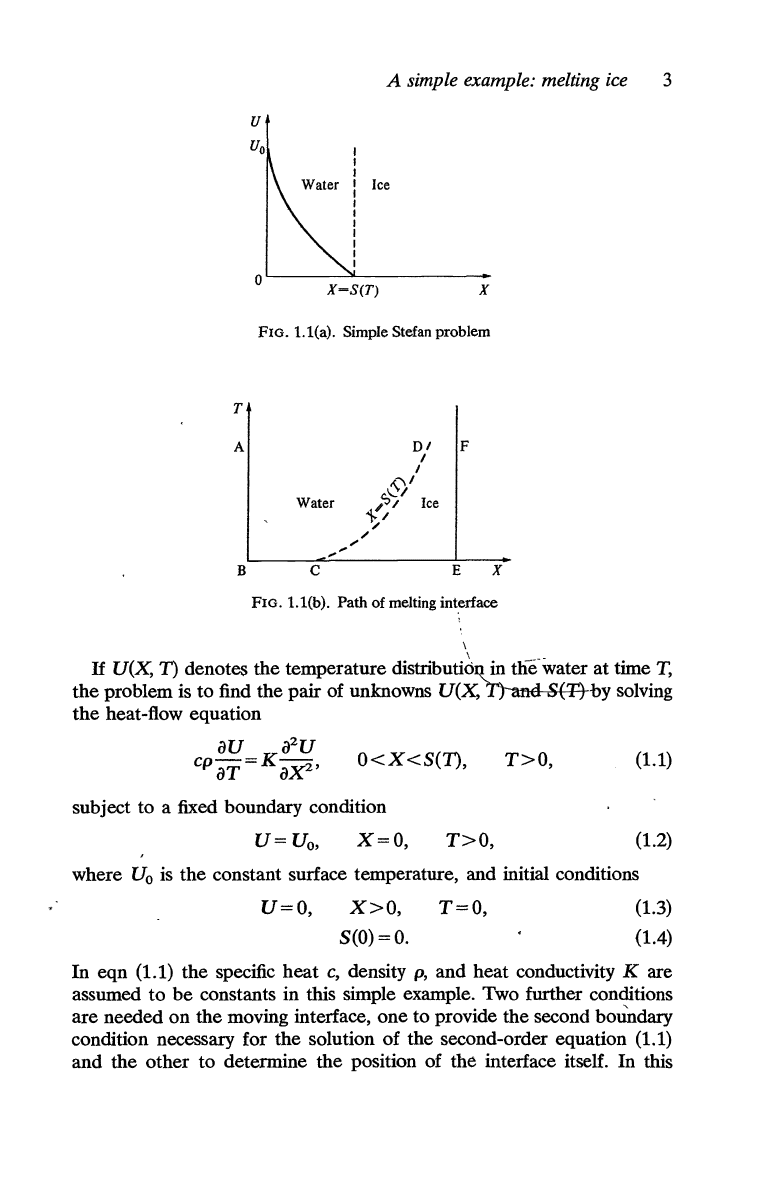
1.2. A simple example: melting ice

1.2.1. Single phase

A simple version of a Stefan problem is

the

melting of a semi-infinite

sheet of ice,. initially

at

the melting temperature, taken

to

be

zero, the

surface of which

is

raised at time T = 0

to

a temperature above zero,

at

which it is subsequently maintained. A boundary surface

or

interface on

which melting occurs, moves from

the

surface into

the

sheet and separates

a region of water from one of ice

at

zero temperature

as

in Fig. 1.1(a).

The

path

of

the

melting interface, S(T), in

the

X - T plane is shown in Fig.

1.1(b), where S(T) denotes

the

thickness

of

the

water phase at time T

and X is

the

space coordinate measured from

the

outer surface of the

sheet,

X=O.

A simple example: melting

ice

3

T

A

B

U

o

Ice

X=S(T)

x

FIG. 1.1(a). Simple Stefan problem

DI

F

1

.<..,,1

"I

Water

/:>/

Ice

;:/

.-

"

,..

C

E

X

FIG. 1.1(b). Path of melting interface

\

..

If

U(X, T) denotes the temperature

distributioI~}n

tile water

at

time

T,

the

problem is

to

find the pair of unknowns

U(X,

'I')-and--Sf'Ftby solving

the

heat-flow equation

au

a

2

u

cp aT=K

ar'

O<X<S(T),

T>O,

(1.1)

subject to a fixed boundary condition

X=o,

T>O,

(1.2)

where U

o

is

the

constant surface temperature, and initial conditions

U=o,

X>O,

T=O,

5(0)=0.

(1.3)

(1.4)

In

eqn (1.1)

the

specific

heat

c,

density

p,

and heat conductivity K are

assumed

to

be

constants in this simple example. Two further conditions

are

needed

on

the moving interlace, one

to

provide the second boundary

condition necessary for the solution of the second-order equation (1.1)

and the other to determine

the

position of the interface itself.

In

this

4 Moving-boundary problems: formulation

problem they

are

u=o,

}

_ K

au/ax

=

Lp

dS/dT

X = S(1),

T>O,

(1.5)

(1.6)

where L is

the

latent

heat

required

to

melt ice. Equation (1.6) is known

as

the

'Stefan condition' and

it

expresses

the

heat balance

on

the

interface

as explained in §1.2.3.

1.2.2. Two phases

If

the

ice is initially

at

a temperature below

the

melting temperature,

not

necessarily uniform,

heat

flow occurs in both

the

water and ice

phases. This two-phase problem is

to

find

the

triple

{U

1

(X, T), U

2

(X,

1),

S(1)}, where U

1

and

U

2

denote temperatures in

the

water

and

ice phases

respectively. A typical example is a finite sheet of ice occupying

the

space

O~S(1)~x~e,

where

• _ 2

aD;_Kau;

G/Ji

at

- i

aXZ

'

i=

1, 2

(1.7)

and, with reference

to

Fig.

1.l(b),

AB

is x = 0,

EF

is X =

e,

CD

is

X=S(T)

and

i=l

refers

to

the

water

phase

O<X<S(T),

and

i=2

to

the

ice phase

S(1)<X

<e.

It

is assumed

that

the

water

and

ice phases

together always occupy

the

space °

~

X ~

e.

The

Stefan conditions

are

U

1

= U

2

=0,

}

K

aU

2

_

K

au

1

=Lp

dS

X=S(T)

2 ax 1 ax

dT'

, (1.8)

(1.9)

and

for

the

time being volume changes

on

melting

are

assumed negligible,

i.e. ice

and

water have

the

same density

p,

so

that

PI

=

P2

= P (see §1.3.4).

1.2.3. The Stefan condition

The

Stefan condition (1.9)

is

easily derived by referring

to

Fig. 1.2

which shows

the

boundary moving a distance ax in time

aT.

In

order

to

U Water Ice

oX

X

FIG. 1.2. Stefan condition

Generalizations

of

the

classical

Stefan problem 5

melt

the

ice contained

per

unit area perpendicular

to

X

in

the

shaded

region

an

amount

of

heat

Lp

5X

is required.

An

amount

of heat

-K

l

5TaU

l

/aX

enters

the

shaded element from

the

water

phase and

- K

2

5T

au

2

/ax

escapes into

the

ice. Assuming

there

are

no

heat

sources

on

the

interface

the

heat

balance of

the

shaded element requires that

(1.10)

which is (1.9).

1.3.

Generalizations of the

classical

Stefan problem

1.3.1. Non-linear heat parameters

Practically important generalized forms of

the

two-phase problem

posed

in §1.2.2 incorporate any

or

all of

the

following non-linear fea-

tures:

(i)

The

heat

parameters in (1.7)

K;,

G,

Pi

may all

be

functions of

U,

X,

T,

e.g. K;(Vi, X, T).

(ii)

On

the

moving interface

the

temperature U

m

may

be

space and

time dependent, i.e.

X =

S(T),

Vi =

Um(S,

T),

i=

1,

2.

(1.11)

(iii)

There

may

be

a

heat

source

q(U

lID

S,

T)

(or sink)

on

the

moving

boundary,-'possibly coupled with variable thermal properties there, e.g.

(1.9) becomes

aU

2

aUl

dS

K

2

(U

m

,

S, T)

ax

-

Kl(U

m

,

S,

T)

ax

=L(U

m

,

S,

T)p

dT

-q(U

m

,

S,

T).

(1.12)

(iv) Body heating terms

h(U, X, T) may

be

required

on

the

right-hand

side of (1.1)

in

a single-phase

problem

or

in each of

the

phases in (1.7).

The

effect of such a

heat

production term may

be

that

there

will no

longer

be

a sharp boundary between

the

liquid

and

solid phases. What

has

been

called a 'mushy' region may develop such

that

the

sharp melting

boundary

is replaced by a finite region throughout which

the

material is

at

its phase-change temperature. Atthey (1974) discusses

the

spot

welding

of

two sheets

of

metal as

an

example

of

a mushy region.

The

sheets are

gripped between two electrodes

and

the

electric current passing between

them

produces joule heating

of

the

metal. This practical situation is

described in detail in §6.2.6

and

used as

an

example

to

illustrate a

convenient way of formulating

and

solving problems containing mushy

,regions.

6 Moving-boundary problems: formulation

Rubinstein (1982a) expressed concern about

the

precise physical sig-

nificance of

the

tenn

mushy region, which is considered to

be

at

a unifonn

temperature

but

has phase changes occurring within it, on

the

grounds

that it is incompatible with

the

concept of a classical solution.

In

the

Stefan boundary condition (1.9), for example, a uniform temperature

means

that

the

right-hand side

is

zero and hence there

is

no rnovement of

the

solid-liquid interface and

no

melting

or

freezing can occur.

If

the

mushy region is considered

to

consist of small solid and liquid regions

separated by many interfaces,

the

solid particles must

be

slightly below

the

melting temperature and the liquid slightly above it, so that local heat

changes occur and new interfaces can

fonn

and existing ones disappear.

Elliott

and

Ockendon (1982) visualize blobs of

pure

liquid and slightly

superheated solid in an unstable equilibrium, with an 'averaged' tempera-

ture being zero over a region containing many blobs

but

fonning only a

small

part

of

the

whole of the mushy region. They draw a comparison

with

the

forming of dendrites

in

the

solidification of alloys. Mathemati-

cally, as in §6.2.6,

the

mushy region has

been

interpreted

to

be

a region

where

the

~ocal

enthalpy takes values in

the

range between those of

the

pure solid and liquid and

the

temperature is uniformly constant and equal

to

the

phase-change temperature.

Rubinstein

(1982a) proposed some more sophisticated mathematical

models of solid-liquid zones in single component media and binary alloys.

Solomon

et

al.

(1982) described a semi-empirical model

of

a mushy

region with an exact similarity solution. They considered a semi-infinite

liquid in

the

region x

~

0 initially

at

its solidification temperature T m and

from time

t = 0

the

temperature

on

the

surface x = 0 is maintained

constant at

T.

<

Tm.

Subsequently,

three

zones are distinguished:

(1)

liquid at temperature Tm in

x~

Y(t); (2) solid

at

temperature T(x,

t)<

Tm

in O:!S;x<X(t):!S;Y(t); (3) the mushy region at temperature

Tm

in

X(t):!S;

x:!S;

Y(t). G,uided by microscopic studies of Thomas and Westwater (1963),

Solomon

et

al.

make the following assumptions; (a)

the

m~terial

in

the

mushy region contains a fixed fraction

(JL

of

the

total latent

heat

L(O <

(J

< 1); (b)

the

width of

the

mushy region

is

inversely proportional

to

the

temperature gradient in

the

solid region at x = X(t), i.e.

{Y(t)-

X(t)}Tx(X(t), t) =

'Y

= constant.

The

constants

(J,

'Y

are

characteristics of

the

material and their assump-

tion of

(J

constant implies a unifonn packing df crystals throughout

the

mushy region. Energy conservation then leads to

Generalizations

of

the

classical Stefan problem 7

Taking

other

conditions

to

be

Yt(x, t) = aTxx(x, t), 0

<x

<X(t)

T(x,t)=T

m

,

X~X(t),

T(O, t) = T

s

, t

>0,

T(x,

0)

= T

m

,

O<x<co,

Solomon et

at

(1982) obtain

the

solution

T(x, t) =

Ts+a

erf(x/2.Jat)/erf

A,

O<x

<X(t)

X(t)=2A.Jat,

Y(t)=211-.Jat,

with

II-

= A +{y.J1Te

A2

erf

A}/2aT

and

A

the

unique

root

of

the

equation

St = \ A2

rf'

y(1-

6).J7I' ( A2

rf

,)2

J;

I\e

e

1\

+

aT

2 e e

1\

•

Here

aT

= T m -

Ts

and

St

=

ea

TIL

is

the

Stefan

number

which is seen to

be

A for values of

the

dimensionless

parameter

y(1-

6)/aT=

(J)

say. Solomon et

al.

plot

St as a function

of

A

for

various values

of

(J)

when

6 = 0

and

also

show

the

dimensionless relative mushy region width

a Til-

-A

.J1Te

A2

erf A

---=-

y A 2 A

as a function of

A.

Primicerio (1981b)

reported

some preliminary thoughts

on

the

theoret-

ical investigation

of

mushy regions in one-dimensional problems and

on

the

possible existence

of

both

classical

and

weak solutions with

or

without

the

presence of distributed

heat

sources.

(v)

The

initial condition may

be

space dependent, i.e. U = Uo(X) at

T = 0,

and

on

any

of

the

fixed boundaries

there

may

be

time dependent

or

non-linear conditions, e.g.

U=f(T)

or

aUlax=c/J(U, T), . X=O. (1.13)

(vi)

Rubinstein (1979)

in

discussing

the

connection between multi-

dimensional Stefan problems

and

the

theory of partial differential equa-

tions of

the

first order, draws attention

to

the

interesting possibility that

the

Stefan

boundary

condition might include a second-order derivative,

e.g.

the

condition (1.9) above could become

L

dS

=K

aU

2

_

K

au

1

_

as

(au

2

_

aU1

)+b

2

a

2

s

PdT

2

ax

1

ax

aY aY aY ay2

8 Moving-boundary problems: formulation

on Y

==

sex,

T)

and b

2

is

a small parameter.

He

quotes a practical

example relating to

the

transfer of fluid across a deformable, semi-

permeable membrane of large curvature. Details of

the

formulation and

numerical solution of such biological problems were discussed by Rubin-

stein (1974) and Geiman and Rubinstein (1974) and surveyed by Rubin-

stein (1980b).

(vii)

Fasano (1980) assembled several of

the

above generalizations and

extensions of Stefan boundary conditions and examined theoretical prop-

erties 'for one-dimensional problems.

He

gave an extensive list of refer-

ences several of which are souices of further reading.

(viii) Results on

the

homogenization of Stefan problems were obtained

by Damlamian (1980).

He

dealt with a mixture of two

or

more media

which have different properties and are laid

out

in a periodic pattern.

He

established new constitutive laws for

the

homogeneous problem ap-

proached in the limit as

the

size of the periodic mesh goes to zero.

1.3.2. Linearized forms

Little systematic work

is

available on

the

cases listed above in which

the

parameters are functions of temperature. Only equations and bound-

ary conditions linearized in

the

sense that the parameters are space and

time dependent have been more widely studied. They provide a good

description of many practical systems; they may also

be

useful

as

approxi-

mations

to

temperature-dependent systems often

as

successive stages of

iterative treatments.

The

'linear' two-phase generalized Stefan problem considered, for

example, by Meyer (1976) is given in

the

region b

l

,,;;;;

X,,;;;;

b

2

by

a (

au

l

)

aU

I

ax

KI

ax

-CI

aT

=

hi>

bl<X<S(T),

T>O,

(1.14)

a

(K

au

2

)

au

2

_

h

aX

2

ax

-

~

aT

-

2,

S(T)<X<b

2

,

T>O,

(1.15)

aU

I

U

1

=

(MT)

ax

+

al

(T),

X==bi>

T>O,

(1.16)

aU

2

U

2

=

f3iT)

ax

+

a2(T),

X=b

2

,

T>O,

(1.17)

where

Ki>

C

I

,

hi>

K

2

,

C2,

~

may

be

functions of X and

T,

e.g. KI

==

KI(X,

T),

etc. Also

U

I

==

I1-I(S(T),

T);

U

2

==

11-2(S(T),

T),

}

K aU

I

_

K

aU

2

+

L

(S(T)

T)

dS

==

(S(T)

T)

X==S(T),

I

ax

2

ax

'

dT

11-3

"

together with initial conditions of any suitable kind.

(1.18)

T>O,

(1.19)

-

Generalizations

of

the classical Stefan problem 9

1.3.3 Non-dimensional forms

So far,

the

variables and

the

heat

parameters have denoted quantities

expressed in physical units, e.g. X in centimetres, T in seconds. Many

authors present Stefan problems in non-dimensional variables.

Thus, introduction of

the

new variables

X

KT

V S

x=-

t=--

u=-

s=-

('

cp

(2'

V

o

'

('

(1.20)

where (

is

some

standard

length, reduces

equations

(1.1-6)

to

the

following:

au

a

2

u

-=-

o<x<s(t),

t>o,

(1.21)

at

ax

2

'

u=l,

x=o,

t>o,

(1.22)

u=o,

x>o,

t=o,

(1.23)

s(O)

=0,

(1.24)

U~O

}

(1.25)

_

au~

=.\

ds

x=s(t),

t>o,

(1.26)

ax

dt'

where .\

=L/(cU

o

)

is

a dimensionless 'latent

heat'

and 1/,\ is

the

Stefan

number.

The

choice of

.\'=

1 implies U

o

= LI

c,

i.e.

the

boundary condition

(1.2)

on

X=O

becomes

U=L/c.

The

two-phase system specified by equations (1.7-9) can

be

similarly

expressed in terms of

the

variables

X

x=-

('

>/

~oT

t=--

CoP

(2'

S

s=-

('

(1.27)

where U

o

,

K

o

,

Co

are any standard values of

the

respective variables.

Then

the

two equations (1.7) become

i = 1, 2,

(1.28)

where

K;

= (KJKo)(co/e;), and (1.8,9) become

U1

=U2=0, }

aU2

_

aU1

_ ds x = set),

"12

ax

1'1

ax -

dt'

(1.29)

(1.30)

where

1';

= KJ(AKo). When

the

heat parameters are not constants, e.g.

~=~(Ui,X,T)

as in §1.3.1,

the

corresponding non-dimensional

parameters are also functions of

the

variables, e.g.

K; = K;(U;,

x,

t),

1';

=

1';

(u(s(t)), set), t).

(1.31)

10

Moving-boundary problems: formulation

1.3.4. Density change and convection

The

physical derivation of

the

Stefan condition (1.10) in §1.2.3 is a

particular case of conservation of energy in which both phases

are

assumed

to

be

incompressible and

at

rest. More generally, across any

phase-change boundary energy, momentum, and mass must

be

conserved.

For

the case of two incompressible phases, one solid and one liquid, of

different densities

PI and

P2

respectively, the mass condition can only

be

satisfied

if

the

liquid phase moves with a velocity v given by

x = s(t).

(1.32)

In

the liquid region a convective term must

be

added

to

the

heat-flow

equation, so that, for example, (1.21) becomes

au

a

2

u

au

at

=

ax

2

-

V

ax·

(1.33)

In

a one-dimensional problem

the

continuity and momentum equations

for an inviscid liquid require that

iJv/ax

=

O.

The

flow problem and

the

convective term are much more complicated in three dimensions.

Equa-

tion (1.33) represents

heat

flow

in one dimension accompanied by con-

vection whatever

the

latter is caused by, and v need not necessarily

be

a

consequence of a density change as in (1.32).

Although density changes occur frequently in practical systems, most

mathematical papers have neglected

to

take them into account. A few

authors have discussed one-dimensional problems. Chambre (1956) as-

sumed

the

solid phase

to

be

stationary

and

to

have an infinite

heat

conductivity so that

no

equations were formulated in it. Similarity solu-

tions were obtained in

the

liquid phase. Horvay (1962) was critical

of

Chambre's physical assumption of an incompressible fluid in a constant

pressure field and produced alternative similarity solutions. Later Horvay

(1965) formulated equations for temperature, velocity, and pressure in

the

liquid phase and included

the

influence of pressure on the freezing

temperature.

Tao

(1979) used a new variable y(x, t) =

(x+

eS(t»/(l

+ e), j

where S(t) denotes the position of

the

phase-change boundary in

the

two-phase system, and e =

(Pz

- PI)/P2, so that y(S(t), t) = S(t), which

simplifies

the

Stefan condition

at

the

moving boundary. Dankwerts

(1950), reported by Crank

(1975a), introduced coordinates

at

rest in

the

two phases and obtained similarity solutions for a number of one.:

dimensional problems in infinite media. Wilson (1982) also used coordi-

nates

at

rest to obtain similarity solutions of a multi-phase problem with

phases of different constant densities. Some details of Wilson's method

and some otlier similarity solutions

are

given in §3.2.

Generalizations

of

the classical Stefan problem

11

-

1.3.5. Ablation and the inverse Stefan

-problem

The

term

ablation refers

to

the

removal of any

part

of

the

surface of a

body by melting

or

evaporation.

In

the

single-phase, melting-ice problem

described in §1.2.1

and

Fig. 1.1(a),

the

water formed

on

melting stays in

position with its

outer

surface

at

x = °

and

occupies

the

region previously

occupied

by

ice. In

the

case

of

an ablating sheet of ice

the

melt is

continuo~ly

and

immediately removed from the surface

and

the

receding

outer

surface of

the

ice forms

the

moving boundary. Ablation occurs

if

a

solid is melted

by

a hot, well-stirred fluid through which

the

temperature

is everywhere uniform. Andrews

and

Atthey (1975a,b) describe

the

formation of a

hole

in

a metal

by

evaporated ablation

produced

by' a

high-power laser

beam

(see §3.6.5(i)).

In

general,

in

one

dimension,

the

heat

input, q(t),

to

the

solid is

prescribed

on

the

unknown ablating boundary x = set). This is a one-

phase Stefan problem.

For

the

ablation of a slab originally occupying

the

space O.s:;x.s:;t

and

with heat,

q(t»O,

falling

on

the

surface, initially at

x = t,

the

equations

have

the

form

au a

2

u

O<x<s(t),

. (1.34)

at

=axz'

u = get),

• au

ds

x = set),

(1.35)

-'-=A-+q(t)

ax

dt

'

u =

4>

(x)

<0,

O<x<t,

t=o,

(1.36)

u=f(t)<O,

x=O,

t>O,

(~.37)

s(O)=t.

(1.38)

An

inverse Stefan problem is

one

in which

the

motion of

the

melting

interface is known

and

some

other

boundary condition has

to

be

deter-

mined, e.g.

to

solve

the

system (1.34-8)

but

with set) a known function of

t

and

f(t)

to

be

determined. Physically,

the

boundary condition

on

x = 0

has

to

be

determined such

that

the

melting interface moves in a pre-

scribed way.

An

alternative inverse problem is

to

determine

the

heat

source q(t)

on

the

melting interface given both set)

and

f(t). A solution of

an

inverse problem is, of course,

the

solution of some Stefan problem and

may provide

an

indirect

method

of solving

the

ablation problem posed by

equations (1.34-8).

In

a wider context,

an

inverse problem can arise

in

a two-phase

situation.

For

example, a direct Stefan probem is

to

solve (1.7), (1.8), and

(1.9)

and

in particular

to

find SeT)

for

prescribed conditions

on

the

fixed

boundaries such as

x=O,

auz/ax

=

-fz(T),

x=t,

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.