Crank J. Free and Moving Boundary Problems

22 Moving-boundary problems: formulation

A slightly

more

general version

of

the

oxygen problem in cylindrically

shaped

sections of tissue is described by GaIib, Bruch, and Sloss (1981).

One

application relates

to

oxygen diffusion after

rubber

tourniquets

are

removed from rabbits

under

anaesthesia

(Rahmer

et

al.

1977).

In

non-

dimensional terms

the

mathematical problem is defined by

the

equations

in cylindrical coordinates

(r,

6)

()e

()2e

1

()e

1

()2e

-=-+--+--+f(r

6 t e)

()t

()r

2

r

()r

r2

()6

2

""

where e(r, 6, t) is oxygen concentration in

the

tissue, f(r,

6,

t,

e) describes

the

rate

of absorption of oxygen, and, with p(6, t) denoting

the

moving

boundary,

r

l

the

sealed capillary radius, and

ro

the

outer

tissue radius

(Fig. 1.6),

()e

e(p,

6,

t) = 0, -

(p,

6,

t) = 0,

--;;

(p,

6,

t) = 0,

()r

()u

()e

.-(rl'

6,

t)=O,

()r

e(ro,

6,

t) = 0.

Also e(r,

6,0)

=

eo(r,

6) specifies

the

oxygen distribution in

the

tissue when

the

capillary surface is sealed.

GaIib

et

al.

(1981) use a semi-inverse

method

to

obtain analytical

solutions. First a mathematical form

for

the

shape

of

the

moving

bound-

ary is assumed.

Then

an expression for

the

concentration e(r,

6,

t) which

satisfies

the

conditions

on

the

fixed boundaries

and

which is zero with

zero normal derivative

on

the

moving boundary assumed is

taken

e.g.

( )

11 ( )

}2

{p(6,

t)-r}3

e

r,

6, t

=21.P

6,

t

-r

3{p(6,

t)-rJ·

FIG. 1.6. Cross-section of capillary, surrounding tissue, and moving boundary

Generalizations

of

the classical Stefan problem

23

The

corresponding absorption function

fer,

8,

t,

c) is found

by

substituting

this expression for c into

the

partial differential equation. Details are

given by Galib

et

al.

(1981).

In

order

to

model different experimental

systems some expressions chosen for

p(8, t) are

'p

=4/(t+

1),

4

t-1

1

P

+----+----

(t+1)o.7

(t+1f

(t+1)6'

p =

(3

+ cos 8)/(t + 1).

Finally Galib et

al.

(1981) used

the

truncation method of Berger et

al.

(1975), described in §6.3

to

obtain numerical solutions for c(r,

8,

t) and

p(8, t) for

the

functions

fer,

8,

c) derived by their inverse method.

The

numerical results checked satisfactorily with

the

analytical expressions

and in some cases with experimental

data

available.

1.3.11. Concentrated thermal capacities

If

a thermally isotropic body A is in contact over

part

of its boundary

SAB

with a second body B of much greater thermal conductivity,

the

temperature in B may

be

considered

to

be

a function

of

time only

and

not

of

the

space coordinates. This is

the

simplest example of what Tichonov

(1950) described as a concentrated capacity B located

on

the

boundary of

A.

More

generally,

the

body B may

be

assumed

to

be

anisotropic with a

thermal conductivity infinitely large along lines orthogonal

to

SAB'

The

the

temperature in B depends

on

the

coordinates of points

on

SAB

as well

as

on

time.

The

boundary conditions

on

SAB

coupling

the

heat-flow fields

in A and B express continuity

of

temperature

and

heat

flux

in

the

usual

way.

The

solution of

the

heat-flow problem in A must satisfy conditions

prescribed

on

the

boundary of A including those on

SAB'

If

the

latter are

written in a form which includes

the

differential equation

to

be

satisfied in

B they contain derivatives

of

order equal

to

or

possibly greater than

the

highest

order

of derivative appearing in

the

differential equation describ-

ing

the

heat

flow in

A.

Tichonov (1950) based his definition of problems

with concentrated capacities

on

the

appearance of these higher-order

derivatives in

the

boundary conditions.

Rubinstein (1971,1979) drew attention

to

the

practical importance of

problems involving concentrated capacities in which phase changes occur.

Thus, relatively thin, oil-saturated strata can

be

considered as concen-

trated

capacities

on

the

boundaries of impermeable rock!;. Tertiary

methods of oil production

lead

to

problems with free boundaries moving

inside a concentrated capacity as paraffin sediments in oil-saturated media

are

melted

by

the

injection of

hot

liquid

or

vapour.

Fasano, Primicerio,

and

Rubinstein (1980) discussed

the

following

24

Moving-boundary problems: formulation

model problem. A thin horizontal layer of a porous medium constitutes a

concentrated capacity on

the

boundary of an impermeable medium.

An

incompressible liquid flows through the porous layer with a prescribed

velocity and causes a phase change which absorbs latent heat

at

a given

fixed. temperature.

The

two phases are liquids with different specific heats.

Fasano

et

al.

(1980) extended a well-known scheme by Lauwerier (1955)

for a similar problem which did not include a phase change. Lauwerier's

basic assumptions were:

(1) horizontal heat transfer. in

the

impermeable medium is negligible

compared with vertical transfer;

(2) in the concentrated capacity temperature changes in

the

vertical

direction are negligible;

(3) horizontal heat conduction can

be

neglected compared with heat-

transfer by forced convection in

the

concentrated capacity.

Fasano

et

al.

(1980) adopted

the

first two assumptions

but

omitted

the

third and took into account both conduction and forced convection.

The

horizontal and vertical coordinates are denoted by x and z

respectively, the thin porous layer occupies the region

-oo<x

<00,

-2h

<

z

<0,

and the surroundirig impermeable medium extends

to

infinity on

both sides.

The

subscript ° refers to

the

impermeable medium and

subscripts 1 and 2 refer

to

the

two liquid phases in

the

porous layer.

The

temperature fields are assumed symmetric with respect to

the

plane

z

=

-h

and only

the

impermeable region z

>0

is considered. Limwerier's

first assumption gives

ko

uo

zz

=

Uo

t

,

-oo<x<oo,

z>o, t>o,

and in

the

porous layer we have

k;Uwc

+

k~U;zz

=

C;U;t

+

c~vUoc,

i=1,2,

U;z

=0,

z=-h,

kiu

1z

=

kouo

z

,

k!u

2Z

=

kouo

z

,

i=

1,2,

z=O,

-oo<x<s(t),

z=o,

s(t)<x<oo,

(1.64)

(1.65)

(1.66)

(1.67)

(1.68)

where

k~,

c~

are respectively conductivities in

the

z-direction and specific

heats

per

unit volume in

the

two liquid phases i = 1, 2, while v in (1.65) is

the

velocity of percolation in

the

x-direction, assumed constant.

On

integrating (1.65) with respect

to

z between

-h

and ° and using (1.66-8)

we obtain

(1.69)

after dropping"

the

dependence

of

"1'

U2

on z by Lauwerier's assumption

(2).

In

non-dimensional variables,

but

retaining

the

nomenclature

X,

z,

U;,

Generalizations

of

the classical Stefan problem

25

equations (1.64) and (1.68) together with necessary boundary conditions

form

the

system

UO

zz

-

UO

t

= 0,

-00< x

<00,

z>o,

t>o,

(1.70)

Ul=

-b1Ulx -

Ult

= - aluOz(x, 0, t),

-oo<x

< s(t),

t>O,

'(1.71)

U2xx

-

b2U2x

-

U2t

= -a2UOz(x, 0, t), s(t)

<x<oo,

t>o,

(1.72)

where

bi'

a;

(i

= 1, 2) are constants and

U1>

U2

are functions of X, t only,

UO(x,

+0, t) =

U;(x,

t),

z=o,

i=1,2,

UO(x,

z, 0) = f(x,

z),

s(O)

=

0,

Ul(X,

0) =

Mx),

-oo<x<oo,

x<O,

t>O,

t=O

u

2

(x,

0) = fz(x),

U

1

(s(t), t) = U2(S(t), t) = 0, t

>0

s(t) = U2x(S(t),

t)-

Ulx(S(t), t), t

>0.

The

compatability conditions

f(x, 0) =

{Mx),

fz(x),

are also assumed.

x<o,} (

x>O,

fl(0)=f

2

0)=0,

(1.73)

(1.74)

x>o,

(1.75)

(1.76a)

(1.76b)

(1.77)

Fasano

et al. (1980) proceeded

to

analyse

the

above problem

but

only

for

the

case in which x = s(t)

is

a known, time-dependent, phase-change

boundary, and

s(t)

is

assumed sufficiently smooth. They defined

U*(x,

t; s) = {Ul(X, t),

u

2

(x,

t),

and

assumed (1.76a) so that

u*(s(t), t; s) =

0.

x .;;;s(t)

x

>s(t),

(1.78)

(1.79)

In

-oo<x<+oo,

for

the

solution uo(x, z,

t)

of equation (1.70) together

with (1.74) and (1.73) written as

uo(x,O, t) = u*(x, t; s), and assuming

f{x, z)

is

con~inuously

differentiable with respect to z, we can write

uOz(x,

z, t) = f(x,

0)(111)-!

exp(-z2/4

t) + r fz(x,

{)N(z,

t,

{,

0)'

d{

-r u*(x,

T;

s)G,Az,

t,

0,

T)

dT,

(1.80)

where N and G are

the

usual Neumrum and Green functions in the

quarter plane

z>O,

t>O.

After integrating by parts the last integral in

26

Moving-boundary problems: formulation

(1.80) and put!ing

**(

)

{

u:(x,

t; s),

U x, t· s =

, 0,

Fasano

et

al.

(1980) obtained

x

=1=

set)

x

= set),

f u*(x,

T,

; s)G,z(z, t;

0,

T)

dT

= f(x, O)N(z,

t,

0,

0)

(1.81)

-f u**(x,

T;

s)N(z,

t,

0,

T)

dT,

which combined with (1.71), (1.72) after letting z

~

0 yields

Uroc-biU;x-U;t=~F(X,t)-~'7T-!f

u**(x,T;s)(t-T)-idT

in D

I

,

i =

1,

2, (1.82)

where

i=l

in

-oo<x<s(t),

i=2

in

s(t)<x<oo,

t>O,

and

F(x, t) =

('7Ttr!

{'" fz(x,

()exp(-e/4t)

d(.

They prove theorems of existence and uniqueness of (1.82). In an

appendix

to

their paper (1980) J. R. Ockendon suggested an asymptotic

formulation of a slightly modified form of

the

above problem in which

the

free boundary is taken

to

be

x = S(z, t),

S=I=

O.

Rubinstein, Geiman, and Shachaf (1980) obtained numerical solutions

of

the

system of equations (1.70-6b). They introduced new coordinates

moving with

the

free boundary given by

~=x-s(t),

"T/=Y,

T=t,

and used an iterative scheme written with x,

y,

t now denoting

the

new

~,

"T/,

T in

the

form

n=1,2,

...

U;=

-(a-sn)u~+{3uo;l=

u~,

n=

1,2

u~(O,

t) = 0, uo(x, 0, t) =

u~(x,

t), n = 0, 1, 2,

...

uo(x, z, 0) = fo(x,

z),

u~(x,

0) =

tex),

n = 0,

1,2,

...

(1.83)

sn(o) = 0, n = 1, 2,

...

u8(x,

y,

t) = uo(x,

z,

t-T);

u?(x, t) = u_i(x,

t-T).

The

fUnctions. uo(x,

z,

t -

T)

etc. used as starting values

for

the

iterative

process come from a previously obtained non-iterative approximation in

which first-order space derivatives are taken at time

t-T(T>O);

e.g.

the

Generalizations

of

the

classical

Stefan problem

27

0.8

0.7

0.6

0.5

0.4

-0.4

-0.3

-0.2

0.10

uo(x,y,O)

0.5

f-----~y

0.4

0.5

-5'

.......

3 4

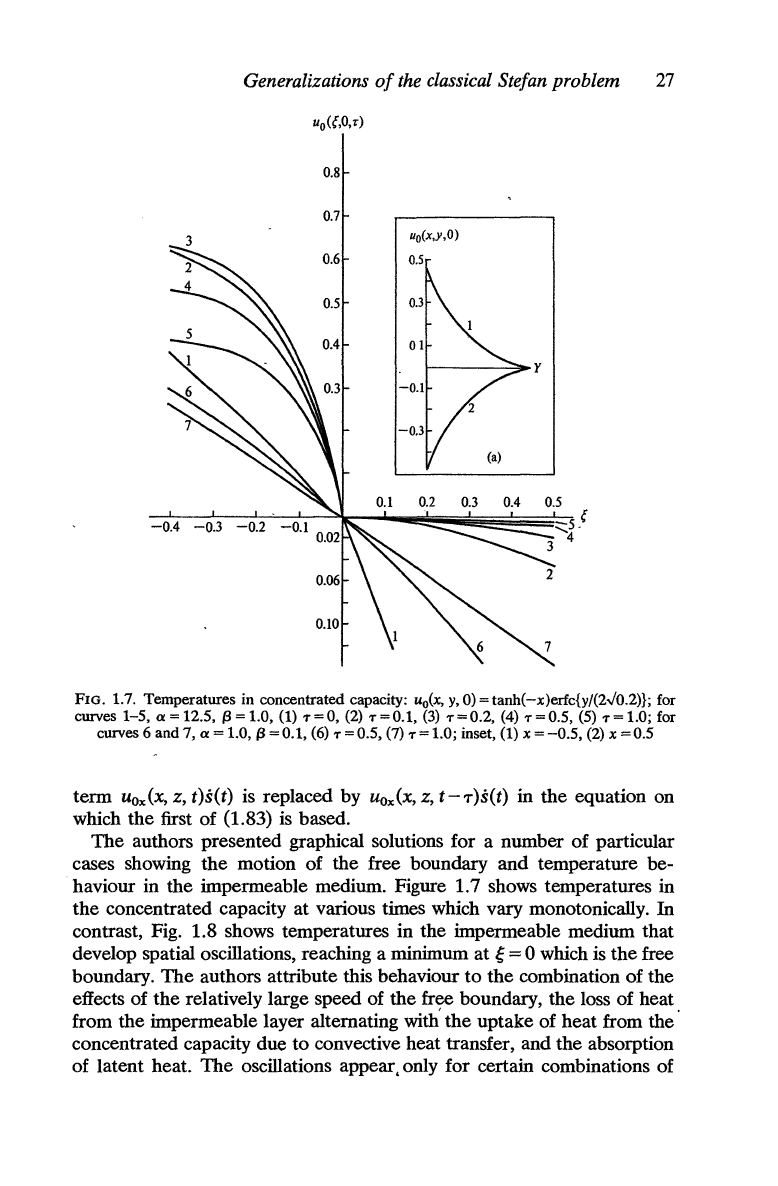
FIG. 1.7. Temperatures in concentrated capacity: uo(x, y,0)=tanh(-x)erfc{y/(2.J0.2)}; for

curves 1-5,

a=12.5,

(3=1.0,

(1) 1"=0,

(2)

1"=0.1,

(3)

1"=0.2,

(4)

1"=0.5, (5) 1"=1.0; for

curves 6 and 7,

a = 1.0,

13

= 0.1, (6)

1"

= 0.5, (7)

1"

= 1.0; inset, (1) X =

-0.5,

(2) X = 0.5

term

UOx(X,

Z,

t)s(t)

is

replaced by uox(x,

Z,

t-T)S(t)

in

the

equation on

which the first of (1.83)

is

based.

The

authors presented graphical solutions for a number of particular

cases showing the motion of the free boundary and temperature be-

haviour in the impermeable medium. Figure 1.7 shows temperatures in

the

concentrated capacity at various times which vary monotonically.

In

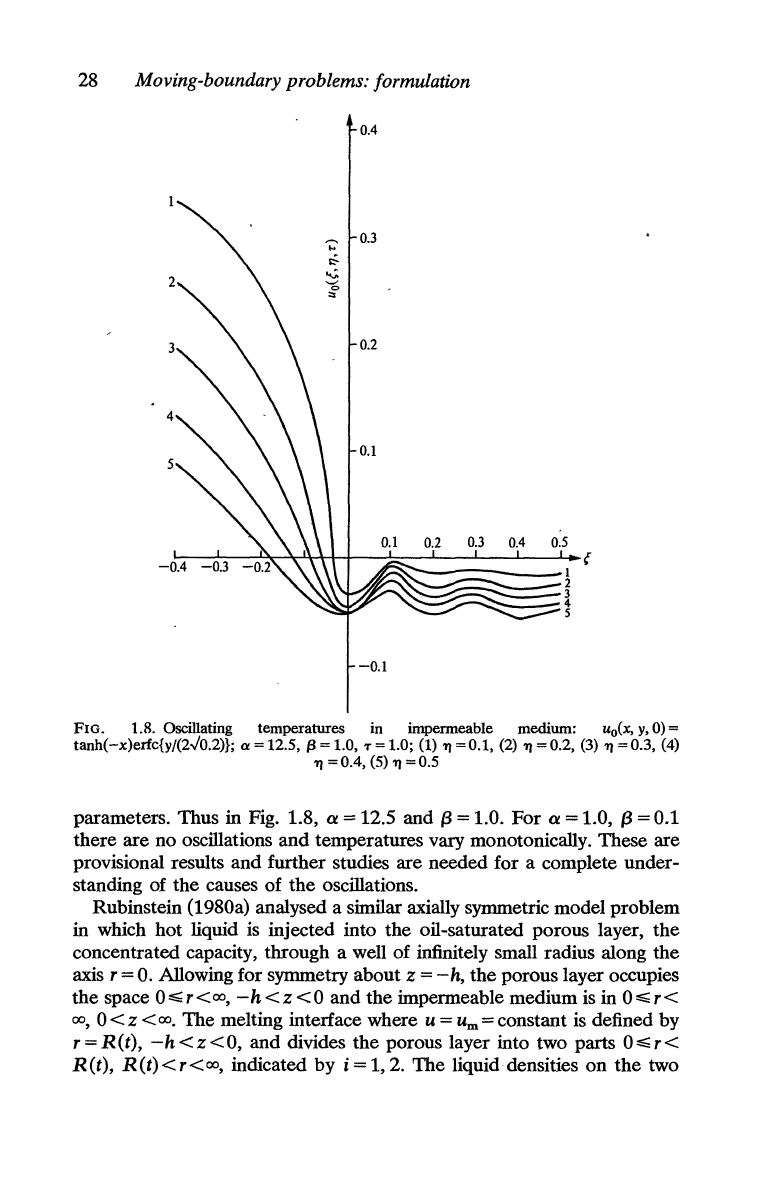
contrast, Fig. 1.8 shows temperatures in the impermeable medium that

develop spatial oscillations, reaching a minimum

at

g = 0 which is

the

free

boundary.

The

authors attribute this behaviour

to

the

combination

of

the

effects of

the

relatively large speed of the free boundary, the loss of heat

from the impermeable layer alternating

with

the

uptake of heat from

the'

concentrated capacity due

to

convective heat transfer, and

the

absorption

of latent heat.

The

oscillations appear, only for certain combinations of

28 Moving-boundary problems: formulation

0.4

2

3

4

5

:----

___

1

2

~~::::.::::'::::::::::~

s

-0.1

FIG. 1.8. Oscillating temperatures in impermeable medium: uo(x,

y,

0) =

tanh(

-x)enc{y/(2v'0.2)}; a = 12.5,

f3

= 1.0,

'T'

= 1.0; (1)

"I

= 0.1, (2)

"I

= 0.2, (3)

"I

= 0.3, (4)

"I

=0.4,

(5)

"I

=0.5

parameters. Thus in Fig. 1.8,

ex

= 12.5 and

(3

= 1.0. For

ex

= 1.0,

(3

= 0.1

there are no oscillations

and

temperatures vary monotonically. These are

provisional results and further studies are needed for a complete under-

standing of the causes of

the

oscillations.

Rubinstein (1980a) analysed a similar axially symmetric model problem

in which hot liquid is injected into

the

oil-saturated porous layer,

the

concentrated capacity, through a well of infinitely small radius along the

axis r

=

O.

Allowing for symmetry about z = -

h,

the

porous layer occupies

the

space

O~r<oo,

-h<z<O

and

the

impermeable medium

is

in

O~r<

00,

0 < Z <

00.

The melting interface where U = U

m

= constant is defined by

r=R(t),

-h<z<O,

and divides

the

porous layer into two parts

O~r<

R(t),

R(t)<r<oo,

indicated by i = 1, 2.

The

liquid densities

on

the

two

Generalizations

of

the classical Stefan problem

29

sides of

the

interface

are

the

same

but

the specific

heats

have different

constant values.

The

following non-dimensional system

of

equations

specifies

the

problem:

Uozz

=

Uo

t

,

O<r<oo, O<z

<00,

t>O,

UirT

+

(1-2v)r-

1

U;.

+

{3Uoz

Iz~o=U;t'

t>O,

i = 1, 2

U1(O,

t) =

h(t),

the

temperature

of

the

injected liquid, t > 0,

U;(R(t),t)=O,

i=1,2,

t>O,

uo(r, 0, t) = u;(r, t), i = 1, 2,

u;(r, 0) = {;(r), i = 1, 2;

uo(r,

z,

0)

=

fo(r,

z),

R(t)

= u2r(R(t),

t)-u

1r

(R(t),

t),

t>O;

R(O)

=Ro>O,

and

10z(0,0)=0;

11r(0)=0;

10(r,0)=[;(r), [;(Ro)=O,

i=1,2;

11(r)

>0,

12(r)

<0;

[;(0) = 0, i = 1, 2;

{3

= constant

>0.

Rubinstein, Geiman, and Shachaf (1980) used

the

same type of proce-

dure

as

for

the

plane case discussed above

to

obtain numerical solutions

for the axisymmetric problem, except that iteration was found

to

be

unnecessary for

the

parameters chosen. No special features were noted.

Rubinstein (1979) formulated a concentrated capacity problem which

he

considered

to

be

a

better,

description

<?f

the

practical oil production

process.

No

analysis

or

numerical solution was attempted.

2.

Free-boundary problems:

formulation

2.1. Introduction

THE

problems introduced in this chapter are not time dependent as in

Chapter

1. Typically, a free-boundary problem consists of a partial

differential equation of elliptic type to

be

satisfied within a bounded

domain together with

the

necessary boundary conditions.

One

section of

the boundary,

the

free boundary, is unknown and must be determined as

part of the solution.

To

make this possible, an additional condition has

to

be

specified

on

the free boundary.

Flow through porous media is an important source of free-boundary

problems, most frequently in relation to seepage phenomena that occur in

nature. Examples are seepage through earth dams; seepage out of open

channels such as rivers, canals, ponds, and irrigation systems,

or

into

wells. Practical interest in free-boundary problems, however,

is

not con-

fined to natural seepage but extends for example

to

topics in plasma

physics, semiconductors, and electrochemical machining.

Free boundaries arise

in

porous

flow

when

the

porous medium

is

occupied by two fluids separated by a sharp interface, which is

the

free

boundary. Water/air interfaces are the most common,

but

water/water

vapour, oil/water, oil/gas, and salt water/fresh water interfaces are also

important. The assumption that a sharp interface exists implies that the

porous

flow

is

saturated, i.e. any particular part of

the

porous medium

is

either saturated by

one

fluid

or

contains none of it, so that there are sharp

interfaces, the free boundaries, between the regions occupied by the

different fluids.

For

example,

in

a saturated water/air

flow

anyone

portion of the medium

is

either wet

or

dry. Free-boundary formulations

of porous

flows

can therefore

be

regarded as approximations

to

partially

saturated

flows

in which

the

fluid content of part of

the

medium may

be

between none and

the

maximum value corresponding

to

saturation.

Sometimes, comparisons between the mathematical solution of a free-

boundary model and

the

solutions for corresponding partially saturated

flows

can indicate whether

the

assumption of saturated

flow

is

justified.

Comprehensive and directly relevant reviews of free-boundary prob-

Simple rectangular dam

31

lems, mainly in the context of saturated porous

flow,

and their solution

are given by Baiocchi

et

al.

(1973a), Cryer (1976a,b), and Bruch (1980),

and each of these is a valuable source of other more detailed references.

Cryer prepared a series of surveys

on

various aspects of free-boundary

problems including Cryer and Fetter (1977), which dealt with the varia-

tional inequality solution of axisymmetric porous

flow

in well problems.

Cryer (1977) compiled a bibliography of free-boundary problems with

five

appendices. Standard references for background information on

porous-flow problems are Muskat (1937), Polubarinova-Kochina (1962),

Harr

(1962), and Bear (1972). Cryer (1976a) gives more specialist

references.

In

this chapter several free-boundary problems are formulated

mathematically and their physical origins are introduced briefly. Discus-

sion of methods of obtaining mathematical solutions

is

deferred to

Chapters 7 and 8 for

the

most part.

2.2. Simple

rectangular

dam

The simplest case of seepage through a dam separating two reservoirs

at

different levels can be regarded as the stationary saturated flow of an

incompressible fluid through a homogeneous isotropic medium. The

simple rectangular dam which has parallel vertical walls and an impervi-

ous horizontal base has been much studied and adopted by many authors

as a model problem for assessing new methods of solving free-boundary

problems.

2.2.1. Qassical formulation: physical derivation

The

physical derivation of the mathematical equations will first

be

given with reference

to

Fig. 2.1. The dam

is

regarded

as

being long

y

r F

Q

~seepage

YI

Seepage

1

region

surface

C

Y2

A B

x

-\"1---

FIG" 2.1. Simple rectangular dam

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.