Crank J. Free and Moving Boundary Problems
Подождите немного. Документ загружается.

62
Free-boundary problems: formulation
Baiocchi et al. (1973b) also proved
that
w satisfies in
i5
the
inequality
O~w(x,
y)os;;~(1_p)y2+!(x-a)(1-p)Yil(pa).
(2.91)
It
follows that
w(x,
y)
is
a solution of
the
variational inequality
J
f[Vw'
V(v-w)]dx
dy
~
- f
J(v-w)
dx
dy
(2.92)
D D
for all v with
the
usual properties and for which v agrees with w
on
the
boundary of D
and
also lies in
the
range in (2.91).
The
converse is
true
and there is an equivalent minimization formulation closely similar
to
(2.42), (2.43) for
the
simple dam.
The
only difference between
the
two
problems is
the
convex space in which w(x,
y)
is
to
be
found.
The
discharge q of
the
aquifer across any vertical section
is
given
by
!
f
1
(X)
-q
=
cPx(x,
1j)
d1j
=
Wx
along
GH
2(X)
=!(1-
p)yi/(pa)
(2.93)
from (2.90c), since
cf>x
= 0 outside f2(X)
os;;
y
os;;fl(X).
Baiocchi et al. (1973a)
used a numerical algorithm similar
to
the
one
for
the
simple
dam
and
they
gave tabulated values of
f2(X),
the
lower free surface in Fig. 2.10(a), for
an aquifer corresponding
to
a practical situation (Table 8.8).
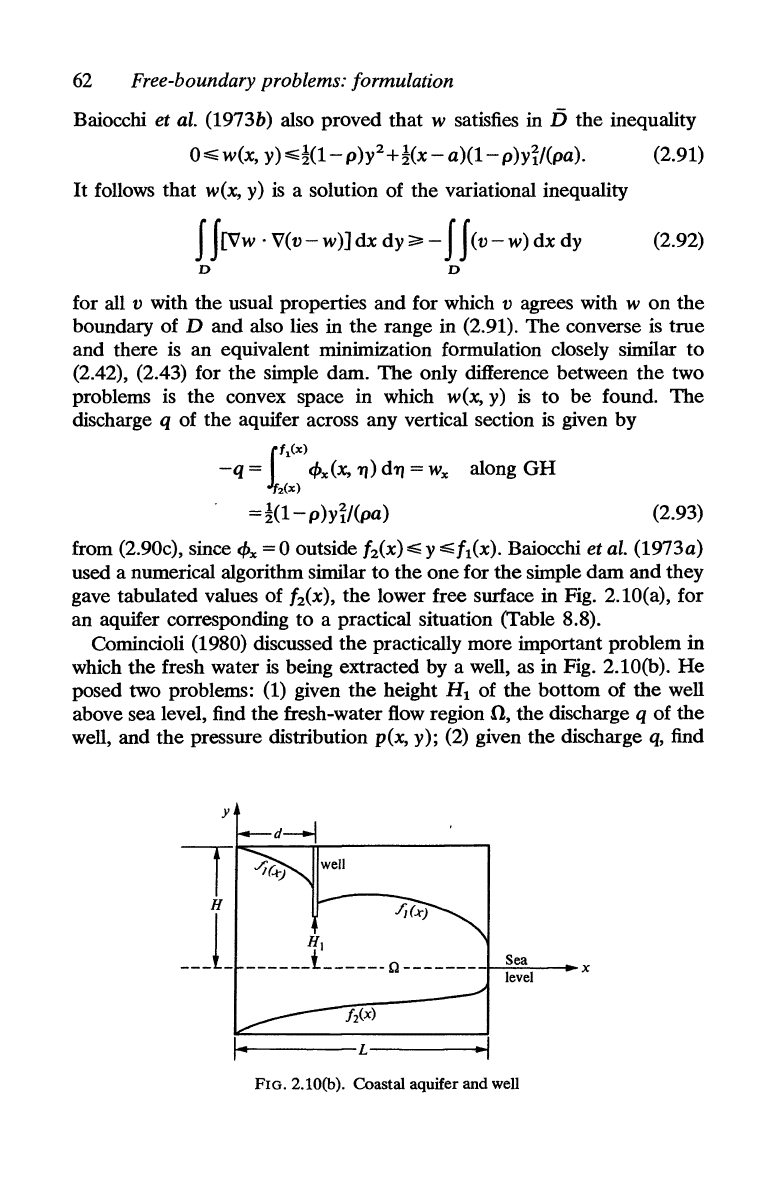
Comincioli (1980) discussed
the
practically more important problem in
which
the
fresh water is being extracted by a well, as in Fig. 2.10(b).
He
posed two problems: (1) given
the
height HI of
the
bottom of
the
well
above sea level, find
the
fresh-water flow region fl,
the
discharge q of
the
well, and
the
pressure distribution
p(x,
y); (2) given
the
discharge q, find
y
HI
------t------!J
________
I---7
S
o::::;ea'-:-_x
level
f2(x)
~--------L--------~·~I
FIG.2.10(b). Coastal aquifer and well

Canals and ditches
63
Hi>
0,
p.
He
finds
that
Problem
(2)
can
be
formulated
as
a variational
inequality and
that
the numerical solution presents
no
difficulties. Prob-
lem
(1)
on
the
other
hand
leads to a quasi-variational inequality and the
iterative method
of
solution has to incorporate a compatability condition,
in order to find
q,
closely similar to condition (2.57) in §2.3.2, and which
ensures continuity of pressure
p.
The discharge of
the
well q
is
given by
q=q(x<d)-q(x>d),
where
q(x)
takes constant values in the intervals
0::;;;;
x::;;;;
d and
d::;;;;
x
::;;;;
L (Fig.
2.lOb) and is defined as in (2.93) by the integral
More details
of
the mathematical and numerical aspects
of
Problems
(1) and (2) are given by Comincioli (1980) and by Baiocchi, Comincioli,
and Maione (1977), who also present some numerical results. The ap-
proach
is
essentially that used by Comincioli (1975) and described above
to
derive (2.69h).
Ground water pollution by the hydrodynamic dispersion of solutes in
aquifers
is
studied by
Bear
(1980).
2.6.
CauaIs
and ditches
Another set of free boundary problems in porous
flow
relates to
seepage from canals
or
ditches through permeable soil into a drain at a
finite depth
or
into a water table. Particular cases of seepage from
trapezoidal and rectangular channels into drains were studied by Bruch et
al.
(1978) who presented numerical algorithms and results based
on
their
variational-inequality formulation. Bruch and Sloss (1978) gave similar
information for a single triangular channel and Bruch
(1979a) considered
an array of parallel identical triangular channels. Bruch
(1979b) obtained
similar results for a single channel over a shallow water table.
The
treatment of all these examples can
be
illustrated by considering a
channel with an arbitrary-shaped bottom, part of which, near the axis of
symmetry,
is
horizontal
as
in Fig. 2.11. Only half the system
is
shown
because of symmetry about the y-axis. Torelli (1974) gave theoretical
results and Bruch (1980) established a variational inequality for the
Baiocchi variable,
w(x, t).
The formulation
is
closely analogous to that of the dam problems
considered in previous sections.
The
flow
region 0
is
ABCF specified by
O<X';;;XF,
O<y
<
Y(x),
together with
XF<X
<xc,
O<y
<f(x),
where
y
==
Y(x)
is
the
equation of the channel bottom and y
==
f(x)
is
the free

(\·4
Frcc-boundary problems: formulation
FIG. 2.11. Seepage from open channel
surface.
The
conditions for
<p
and
1/1
are
<Px
=
I/Iy,
<P
y
= -
I/Ix
in n
<p
=0
on
Be,
.
<p
= yp = Y(xp) on AF,
<p
=
y,
1/1=0
on Fe,
1/1
=!q
on AB.
(2.94a)
(2. 94b)
(2.94c)
(2. 94d)
(2. 94e)
The reason for
the
condition (2.94b) on the drain
Be
is
the
same as for
(2.50c) on a toe drain.
Bruch (1980) suggested the region
ABDE
is
a convenient
one
to
take
as the extended domain D for numerical work and extensions of the
variables
<p
and
1/1
are defined as usual
by
4>
=
<p
in
0"
4>
= y in .z5-0,;
~
=
1/1
in 0,
~
= 0 in V - 0.
The
formulation in terms of w(x, t) defined as
usual
is
V
2
w=
1 in
n,
w>O
in
n,
~w=O
in
D-n,
w=O
in
V-O,
Wx
=-~,
Wy
=
Y-4>
in D,
Wy
=0
on
Be,
Wy
=
y-yp
on AF,
WX
= -!q on AB,
(2.95
a)
(2.95b)
(2.95c)
y =
Y(x),
(2.95d)
(2.95e)
since
Be
is
only half
the
complete drain. Because q is unknown a priori, a
compatability condition is needed. Bruch and Sloss (1978) derived
the
condition
(2.95f)
for a triangular channel, which applies also
to
the present problem;

Canals and ditches
65
WN,M-l
denotes w(x, y) at the point N dX,
(M
-1)
dy
on
a mesh for
which
xF=N
..ix,
YF=M
dy. They discretized the expression for the
discharge
and, following the derivation of (2.56) in §2.3.2, incorporated the dis-
cretized form of (2.95e), (wO,j-W-IJ)/..iX=-!q, where
jdY=YA,
to
produce (2.95f).
With
v(x, y) having
the
usual general properties and with
v;;;:.
0 in D,
v = 0
on
FE
and
ED,
and
defining for convenience (3(x, y) = (y/Y) dY/dx,
{3
= 0
on
AB,
BD,
where
the
second derivatives are continuous in
D,
the
variational inequality formulation
is
J
Jvw
'V(v-w)dxdy;;;:'-
J
J(V-W)dXd
Y
D D
-
r(1+Y~)(Y-YF)(V-W)dx-!q
J:(V-W)d
Y
. (2.95g)
Computational details
and
some numerical results for channels of
particular rectilinear shapes are
to
be
found in the references given at the
beginning of this section. These papers contain also many references to
other
relevant papers.
The
SOR algorithm with projection given in
equations (8.90), (8.91) in Chapter 8 is coupled with use
of
the secant
method (8.97)
to
handle compatability conditions
of
type (2.95f).
Where
the
drain
Be
is replaced by a water table (Bruch 1979b), the
base becomes impermeable and Fig. 2.12 indicates
that
the free surface
FE
must become asymptotically parallel to the water table. Bruch made
the
assumption that
at
x = L the free surface
is
not quite horizontal and
that, in order
to
carry away the seepage fluid and make a steady-state
flow feasible, the base has a downward slope beyond
x =
L.
Furthermore
y
B
r-_~F~
____________
IE'
I
I
I
I
I
I
I
I
IE
C
!--I.-----L~-----
_-
_-
_-
_-
o--j-f'=----
x
FIG. 2.12. Channel over shallow water table

60
Free-boundary problems: formulation
DE
was taken
to
be
an
equipotential line. Again, the discharge q
is
not
known and a compatability condition
is
needed. Bruch (1979b) gives
details of a Baiocchi-type formulation with a numerical scheme and com-
pares results with other published data. Bruch and Sloss (1981) applied
their split-field method (§2.3.8)
to
seepage from open channels.
There
is
the added advantage that a compatability condition
is
not needed because
the condition (2.95e)
is
replaced by
cPx
= 0 on AB and q can
be
found
from
the
solution. Seepage from partially lined canals
is
studied by Bruch
and Mirnateghi (1982).
2.7.
Axisymmetric Bow
Free boundary problems in which
the
porous
flow
is radial are provided
by seepage into wells and
out
of ponds. Wells have been extensively
studied and standard general references are Polubarinova-Kochina
(1962),
Harr
(1962), Hantush (1964). Cryer (1976a), and Cryer and
Fetter (1977) give an extensive list of references to analytical and
numerical solutions. Jeppson
(1968a,c), Neuman and Witherspoon
(1970), and Remar
et al. (1982) discuss axisymmetric seepage from a
pond
by numerical methods.
When an axisymmetric well
is sunk in a porous layer
or
aquifer,
the
water in
the
aquifer
flows
towards the well from which
it
is
removed by
pumping.
After
a time the flow becomes steady and
the
water level in
the
well is maintained
at
a constant height hw.
The
assumption of saturated-
unSaturated
flow
is
made here as in
the
dam
problem. A free boundary,
the positIon of which
is
to
be
determined, separates the upper,
dry
part
of
the aquifer from
~he
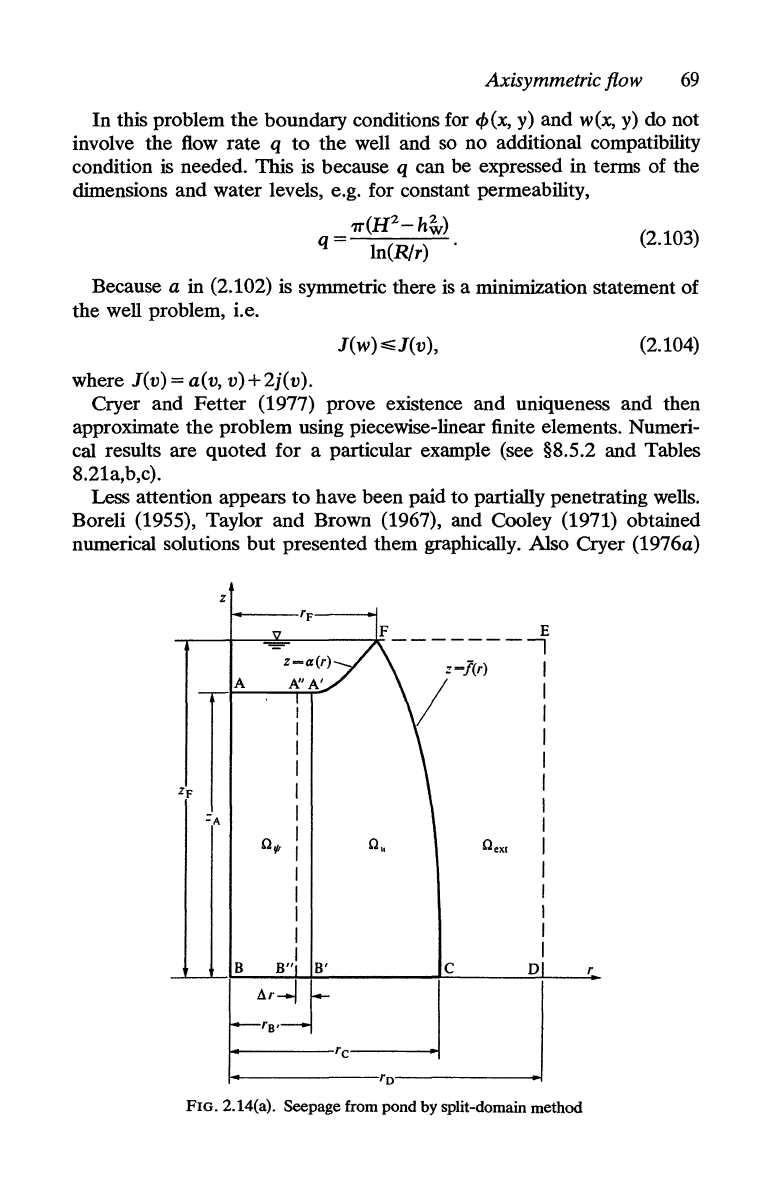
wet, saturated lower part. Figure 2.13 shows half
the
symmetric situation and illustrates
the
nomenclature.
In order to preserve a steady state,
the
water pumped from
the
cell
must
be
balanced by a
flow
into a surrounding region of radius R in Fig.
2.13.
It
is usual
to
assume
that
outside this region the water is effectively
~~~
____________
~B~L-~X
~-------R--------~~I
FIG. 2.13. Fully penetrating well

Axisymmetric flow
67
stationary, and
that
the velocity potential for
x;;"
R
is
q,
= H = constant.
The
well
is
seen to
be
the axially symmetric equivalent of a rectangular
dam, and there
is
a seepage face
DE
at the well. Thus, at the well face,
x =
r,
it
is assumed
that
q,
=
hw
if y
~
hw and
q,
= y if y
;;.,
hw.
In
practice,
wells are often lined by a porous material and the resulting reduction in
flow can
be
allowed for empirically by putting
q,
= y +
q,e
on the seepage
face, where
q,e
is a positive constant. The radial form
of
Laplace's
equation has to
be
satisfied by
q,(x,
y), the velocity potential, but other-
wise the mathematical formulation
is
essentially the same as for the
simple dam in §2.2 and equations (2.7-12). The formulation of
the
well
problem as posed by Cryer and Fetter (1977), allowing for a variable soil
permeability,
is
div(k grad
q,)
=
~
(k
aq,)
+~
(k
aq,)
= 0 in
n,
ax
ax
ay ay
q,
=H
on
AB,
q,
=
hw
on
CD,
q,
= y on
DE,
aq,/ay = 0
on
BC,
q,
=
y,
aq,/an
=0
on
EA.
(2.96a)
(2.96b)
(2.96c)
(2.96d)
(2. 96e)
The
condition (2.96d) implies that the well extends to the bottom of the
aquifer and
is
called a 'fully penetrating well'. A partially penetrating well
is mentioned later.
As
usual, n
is
the unknown
flow
region, 0 < y < f(x),
r < x < R.
The
form of eqn (2.96a) implies that k = xK, where K
is
the
soil permeability. Cryer and
Fetter
(1977) postulate that k
is
of the form
k(x,
y)=exp{y(x)+g(y)} (2.97)
where y(x) and g(,,) are continuously differentiable and g'(y)
;;.,0.
For
the
particular case
of
constant permeability, K = 1 say, then k(x,
y)
= x =
exp(In
x)
and
y(x)
=
In
x,
g(y)=O. (2.98)
A weak solution of the well problem is the function
q,(x, y) which
satisfies
ffkVq,'VVdxdY=O
n
(2.99)
for all functions
vex'
y)
which satisfy the usual general conditions and
which agree with
q,
on
AB, CD,
DE.
The solution
q,
of (2.99) satisfies
(2.96b), (2.96c), and
q,
= y
on
EA.
Cryer and
Fetter
(1977) following Benci (1973, 1974) express the weak
problem
as
a variational ineqUality. The appropriate Baiocchi variable

68
Free-boundary problems: formulation
defined
on
the rectangular domain D given by r < x < R, 0 < y < H is
rf(x)
w(x,
y)=].
exp(g(11))[</>(X,
t)-11]d11 in
0,
y
=0
in
D-O.
(2.100)
By arguments similar to those used in §§2.2.3 and 2.2.4 Cryer and
Fetter
(1977) give
the
detailed derivation of a differential equation for w(x, y)
and then of the corresponding variational inequality. The formulation
of
the well problem finally takes
the
form
where
Lw(x,
y)
= (exp[
I'(x)-
g(y)]wx)x + (exp[
I'(x)-
g(y)]wy)y
=exp[l'(x)]
in fl, (2.101a)
Lw=O
in
D-fl,
(2.101b)
Wx
=
Wy
=
aw/an
= 0
on
EA,
w(x,H)=O
on
FA,
w(R,
y)=
fHeXP(g(t))(H-11)d11
on
AB,
y
w(r,y)=
IhweXP(g(t))(hW-11)d11
on
CD,
(2.101c)
(2.101d)
(2.101e)
(2.101£)
w(r,
y)=O
on
DE,
(2.101g)
w(x, 0) = w(r, 0) + {w(R,
0)-
w(r, O)}F(x)/F(R)
on
CB,
(2.101h)
F(x)
= fexP[-I'(11)]d11,
(2.10li)
in
0 provided
g'(y);;;.O.
Introducing functions
v(x,
y);;;.O
which together with their first deriva-
tives are square surnmable
on
D and which agree with w(x, y)
on
jj
there
follows the variational inequality statement
a(w,
v-w)+j(v-w);;;'O,
(2.102)
where
a(u,
v)=
J
Jex
P
[I'(x)-g(y)]
grad u grad v dx dy (2.102a)
D
and
j(v)
=
JJex
P
[I'(x)]VdXdY.
(2.102b)
D
Axisymmetric flow
69
In
this problem
the
boundary conditions for
c/>(x,
y)
and
w(x, y) do not
involve
the
flow
rate
q
to
the
well
and
so no additional compatibility
condition is needed. This is because q can be expressed
in
terms
of
the
dimensions
and
water levels, e.g. for constant permeability,
7T(H2_h~)
q = In(R/r)
(2.103)
Because a in (2.102) is symmetric there
is
a minimization statement
of
the
well problem, i.e.
J(w)".;;J(v),
(2.104)
where
J(v)
= a(v,
v)+2j(v).
Cryer
and
Fetter
(1977) prove existence
and
uniqueness
and
then
approximate
the
problem
using piecewise-linear finite elements. Numeri-
cal results are
quoted
for a particular example (see §8.5.2 and Tables
8.21a,b,c).
Less attention appears
to
have been paid to partially penetrating wells.
Boreli (1955), Taylor
and
Brown (1967), and Cooley (1971) obtained
numerical solutions
but
presented
them
graphically. Also Cryer (1976a)
z
F E
-.--+-.....,..;~----iC-
- - - - -
--,
A
I
I
I
I
I
I
I
I
OIl
OeXl
I
I
I
I
I
I
B B' B'
CDr
FIG.2.14(a). Seepage from pond by split-domain method
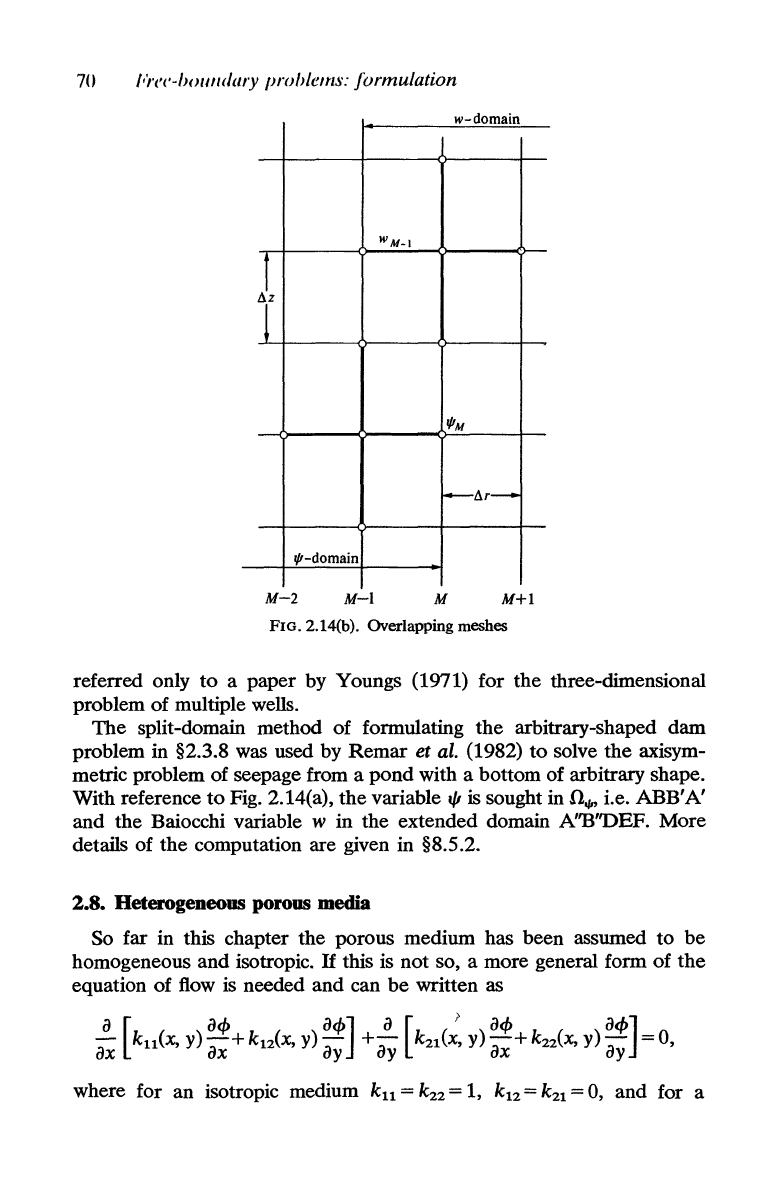
70
"r('('-holilldary
proMem,\':
formulation
d
w-
omam
WM_I
~t
T
J/!M
-~r-
J/!-domain
M-2
M-i
M
M+i
FIG.
2. 14(b).
Overlapping
meshes
referred only
to
a paper by Youngs (1971) for the three-dimensional
problem of multiple wells.
The split-domain method of formulating the arbitrary-shaped dam
problem in §2.3.8 was used by
Remar
et
al.
(1982)
to
solve the axisym-
metric problem of seepage from a
pond
with a bottom of arbitrary shape.
With reference
to
Fig. 2.14(a),
the
variable",
is
sought in
n.",
i.e. ABB'A'
and the Baiocchi variable
w in the extended domain A''B''DEF. More
details of
the
computation are given in §8.S.2.
2.S. Heterogeneous porous media
So far in this chapter the porous medium has been assumed to
be
homogeneous and isotropic.
If
this is not so, a more general form of
the
equation of flow
is
needed and can
be
written as
where for an isotropic medium
kll
=
k22
= 1,
k12
=
k21
= 0, and for a
Heterogeneous porous media
71
homogeneous medium k(x, y) is a constant. An example
of
one
kind of
inhomogeneity has
been
discussed in §2.7, where k(x, y) is
of
the
form
k
1
(x)k
2
(y). Before
the
work
of
Cryer
and
Fetter
(1977), Benci
(1973, 1974)
had
solved
the
rectangular dam problem for this type of
k(x, y) function.
Other
treatments are by Baiocchi (1976) and Baiocchi
and
Friedman (1977).
Other
cases
of
practical importance
and
for which solutions have been
obtained
refer
to
stratified porous media.
The
permeabilities have differ-
ent
constant values in different strata
and
so k(x, y) is a discontinuous
function. Problems in horizontally
or
vertically stratified dams have
received attention by various authors including Baiocchi et
al.
(1973a,b),
Kikuchi (1977), Caffarelli
and
Friedman (1978a,b),
Harr
(1962), Jeppson
(1968b, 1969). Mauersberger (1965),
and
Neuman and Witherspoon
(1970). Outmans (1964) obtained flow rates for stratified dams.
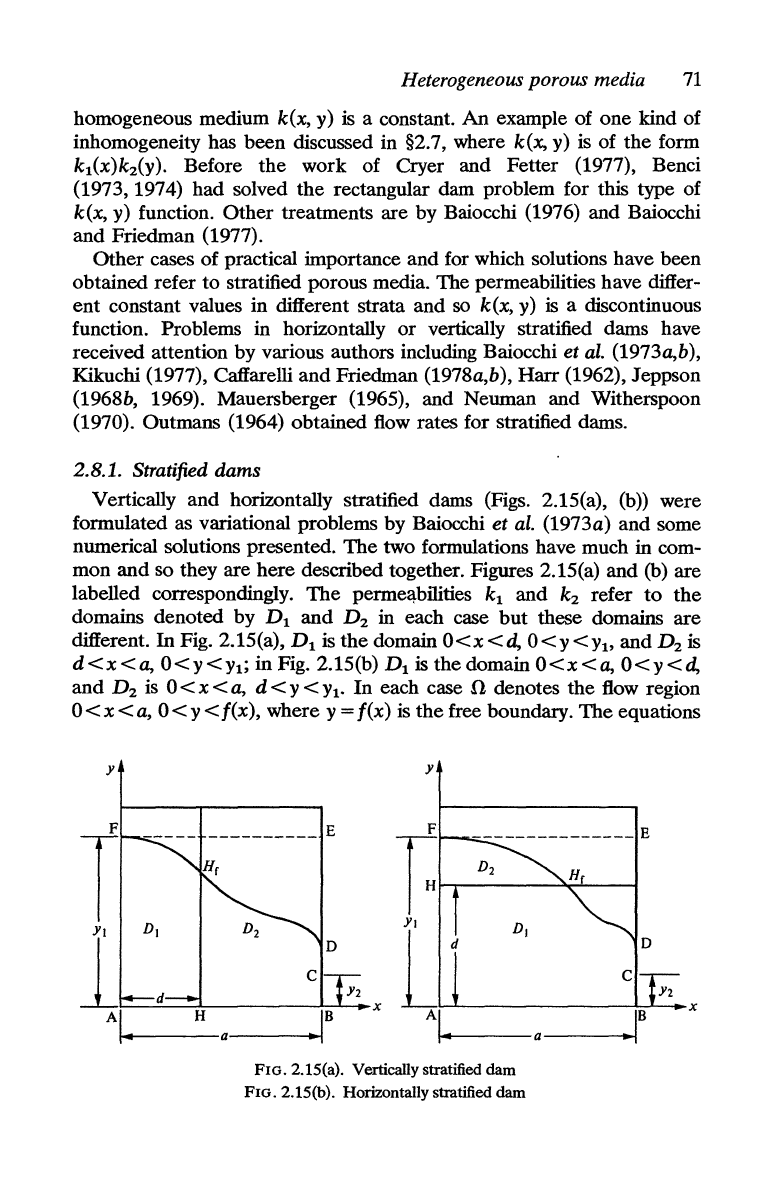
2.8.1. Stratified dams
Vertically
and
horizontally stratified dams (Figs. 2.15(a),
(b»
were
formulated as variational problems by Baiocchi et
al.
(1973a)
and
some
numerical solutions presented.
The
two formulations have much in com-
mon
and
so they are
here
described together. Figures 2.15(a)
and
(b) are
labelled correspondingly.
The
perme~bilities
kl
and
k2 refer
to
the
domains
denoted
by
Dl
and
D2 in each case
but
these domains
are
different.
In
Fig. 2.15(a),
Dl
is
the
domain O<x
<d,
O<Y<Yl'
and
D2 is
d<x<a,
O<Y<Yl;
in
Fig. 2.15(b)
Dl
is
the
domain
O<x<a,
O<y<d,
and
D2
is
O<x<a,
d<Y<Yl'
In
each case n denotes
the
flow region
0<
x <
a,
0 < Y < f(x), where Y = f(x) is
the
free boundary.
The
equations
y
y
~~--~--------~
__
x
~------------~~-.x
~------a----~~
\4------a----~~
FIG. 2.1S(a). Vertically stratified
dam
FIG. 2.1S(b). Horizontally stratified dam
