Crank J. Free and Moving Boundary Problems

72

Free-boundary problems: formulation

and conditions common to the two dams are

~

(k

aq,)+~

(k

aq,)

= 0 in fi,

ax

ay

where

k =

k1

in

Dl

and k =

kz

in D

2

,

q,

=

Y1

on

AF,

q,

=

Y2

on

BC,

q,=y

on

CD

andFD,

aq,/an

= 0

on

AB

and FD.

The appropriate weak solution is

f f

k(aq,

av

+

aq,

av)

dx

dy = 0,

ax

ayay

n

(2.105)

(2.106)

(2.107)

(2.108)

(2.109)

(2.110)

where

v(x,

y) has the usual properties in D and vanishes on

AF

and BE.

II

we denote by

fi1

the

part

of

fi

in

Dl

and by q,l the variable

q,(x,

y) in

fil>

with similar significance for

~

and

q,2,

then (2.110) implies

VZq,l

= 0

in

fil>

VZcf>2

= 0 in

~,

and also the continuity conditions

on

~,

which

are

k1

aq,l/aX

=

k2

acf>2/ax

in Fig. 2.15(a), and

kl

aq,l/ay =

k2

acf>2/ay

in Fig.

2.15(b).

The

usual extension

of

q,(x,

y)

is

defined for both dams by

c$(x,

y) =

q,(x,

y) in n

";"y in

D-n,

but the details of the rest

of

the

formulation are different for

the

two

cases.

For

the vertical stratification (Fig. 2.15(a» the Baiocchi variable is

defined

as

for the simple dam by

w(x,

y)=

f"rci>(x,

Y)-1'I]d1'l

inD.

(2.111)

y

It

satisfies the equation

~

(k

aw)+~

(k

aw)

= k in

fi

ax

ay ay

= 0 outside fi,

and the following conditions

W=i(Yl-y)2

on

AF,

w=!(y~_y)2

on

BC'}

w

=hi-qx/k

1

on

AH,

(2.112)

w =bi+q(a-x)/k2

on

HB,

w = 0 elsewhere on the boundary of D.

Heterogeneous porous media

73

It

can

be

proved

that

the function k 1o(x)

<bx(x,

'11)

d'l1

is

a constant,

denoted by

-q,

where q

is

the

flow

rate and

kIk2(Yi-y~

q = 2[dk

2

+(a-d)k

1

]'

(2.113)

The appropriate variational inequality is

ff

k[oW

(ov _

OW)+

oW

lov _

OW)]

dx dy

+ffk(V-

w) dx

dy;;;oO.

(2.114)

oX oX

oX

oy

\ay

oy

D D

For v(x,

y)

satisfying

the

usual conditions in these problems (2.114) has a

unique solution with a continuous first derivative

on

D.

The

equivalent

minimum problem is to find

W such that J(w)=o;;J(v), where

For

the

horizontal stratification (Fig. 2.15(b)), a necessary modified

definition of

w(x, y) is

(2.115)

It

satisfies

the

equation

k[.i.

(.!

OW)+.i.

(.!

OW)]

= k in

fl

oX

k

oX

oy

k

oy

= 0 outside fl,

and

the

following conditions

on AF,

onBC,

(2.116)

w = 0 elsewhere on the boundary of D

We recall that

k is

the

function which takes the values kl in

DI

and

k2

in

D

2

•

So far in formulating the problem for horizontal stratification it has

been supposed

that

k2>kI>0. This condition

will

be

mentioned later in

74

Free-boundary problems: formulation

this section. Again, the function

J~(X)

k(

T/)</>x

(x,

T/)

dT/

is constant through-

out the dam and equal to

-q,

where

q=~{(YI-Y:J

f2k(T/)dT/+

('

k

(T/)(YI-T/)dT/}.

(2.117)

In

this case

the

variational inequality

is

Jf

.!

raw (av - aw) +

aw

(av -

aw)]

dx

dy +

JJ(

v - w) dx dy ;a.

0'

(2.118)

k

ax

ay

,

D D

with the usual restrictions

on

v(x, y). There is a unique solution for

w(x, y), continuous

on

D.

The

equivalent minimum problem this time is

J(w)~J(v),

where

J(v)

=~

J

J~

[(!:r

+

(!;YJ

dx

dy + J J v dx dy.

D D

(2.119)

For

the case

kl

>

k2

theoretical results appeared not

to

be

complete

(Baiocchi

et

al.

1973b)

but

Baiocchi et

al.

(1973a) concluded from their

numerical results that

the

method can

be

applied even though k

1

> k

2

•

Some results are extracted in Tables 8.9-12.

2.9.

Evaporation

or

infiltration

Porous flow through a simple rectangular dam between two reservoirs

when evaporation of water from

the

free surface

or

precipitation

on

to

it

occurs, has been studied by a few authors, chiefly by Pozzi (1974a,b).

Friedman (1976)

and

Jensen (1977) examined the shape

of

the

free

boundary which is non-monotone in general.

Pozzi

took

evaporation into account by replacing

the

usual condition

ac/>/an

= 0

or

1/1

= 0 on tIle free surface, y = f(x), by

the

condition

1/1

= ex

or

where e is

the

evaporation rate.

He

used the Baiocchi formulation by

introducing the extended variables

c$

and

.fr

defined by

c$(x,

y) =

c/>(x,

y),

.fr(x,

y) =

I/I(x,

y)

in.o,

c$(x,

y) =

y,

.fr(x,

y) = ex in D -.0.

The

Baiocchi variable is defined

by

(2.20)

in'..-§2.2.3

or

by

the

modified

form of (2.46)

w(x,

y)

= k

[cg-

.fr(~,

T/)]

d~

+

J£B

[T/

-c$(~,

T/)]

dT/,

Unsaturated flow: capillary fringe

75

which is still independent of

the

path of integration.

The

differential

relationships for

w(x, y) are

VZw

= 1 + c in

n,

VZw

= 0 in

15

-

n,

w>O

inn,

w=O

inD-n.

The

corresponding variational inequality for w(x,

t)

is

I

fvw

'V(v-w)dxdy-(1+c)

II(v-W)dxdY,

D D

and

the

variables

c{>

and

'"

can

be

regained from

the

solution by using

c{>(x,y)=y-wy(x,y),

",(x,y)=cx-wx(x,y)

inG.

Boundary conditions for several values of

the

evaporation rate c are

given by Pozzi

(1974a).

He

investigated mathematical properties and

obtained some numerical results using the Cryer algorithm.

Pozzi

(1974b)

observed

that

the problem of

the

dam when there is

infiltration

or

accretion (c < 0), e.g. due

to

min,

may not

be

well posed

as

usually formulated

and

this may

be

true

if

the rate of evaporation is too

large. With an impervious base, Pozzi found

that

if

>

(

Yl+Y2)2 _

C

--

=C3

b-a

with reference

to

Fig. 2.1,

the

free boundary has three line segments:

from

(a,

Yl)

to

(a,O), (a,O)

to

({3,0), and

«(3,0)

to

(b,

Y2),

where a

and

(3

can

be

calculated explicitly. H c <

C3,

the free boundary does not meet the

x-axis

but

is non-monotone in general. Friedman (1976) considered

the

more general case which permits a porous base

to

the

dam through which

water can move

at

a

rate

t(x);

if

t(x»O

water moves downwards and

upwards

if

t(x)

< 0, corresponding

to

a boundary condition

(ac{>lay)y=o

=

At(X),

a<x

<b,

A non-negative. Friedman's main result was that

if

c;;;oO,

At(x)~1,

At(X)+C

;;;00,

and

if

the

free boundary does not meet

the

axis,

there exists a number

a,

a<a~b,

such that

f(x)

is strictly monotone

decreasing

if

a

~x

~a

and

f(x)

is strictly monotone increasing

if

a

~x

~

b;

if

a <

b,

f(b)

=

Y2'

Jensen (1977) generalized

the

work of Friedman and

Pozzi

and

determined regions where

f'(x);;;OO

and

f'(x)~O;

he

estimated

the

number of sign changes of

f'(x).

2.10. Unsaturated Sow: capillary fringe

So far in this chapter it has been assumed that

the

flow is saturated, i.e.

the

porous medium is either wet

or

dry.

In

some practical situations the

porous flow is unsaturated

and

some allowance for the presence of air in

76 Free-boundary problellls: forlllulation

the

flow region must be made.

In

order

to

avoid

the

general two-phase

flow problem which is complicated

and

may not be a free-boundary

problem (see §§2.11 and 8.6)

the

idea of a 'capillary fringe' was intro-

duced (see Bear 1972).

It

is assumed

that

the

flow is unsaturated only in a

narrow zone, the capillary fringe, above

the

water level

or

table.

The

term

is used because the fringe zone is attributed

to

capillary forces which draw

up

the water in the porous medium as happens in a capillary tube.

Three

regions are distinguished, namely

the

saturated region,

the

capillary

region,

and

the

dry

region.

It

is assumed that the governing equations are

the

same in

the

capillary

and

saturated regions.

The

unknown free

boundary is

the

interface between

the

dry

and capillary regions.

The

pressure is still taken to

be

zero

on

the

boundary between

the

saturated

and

capillary regions.

In

the

fringe

the

pressure is negative:

-Pc,

where

Pc

is

the

known capillary pressure. Thus the expression (2.5) in §2.2.1

defining

cP

becomes

cP

=

y-pd(pg)

= y

-Yc,

(2.120)

where

Yc

is

the

capillary rise.

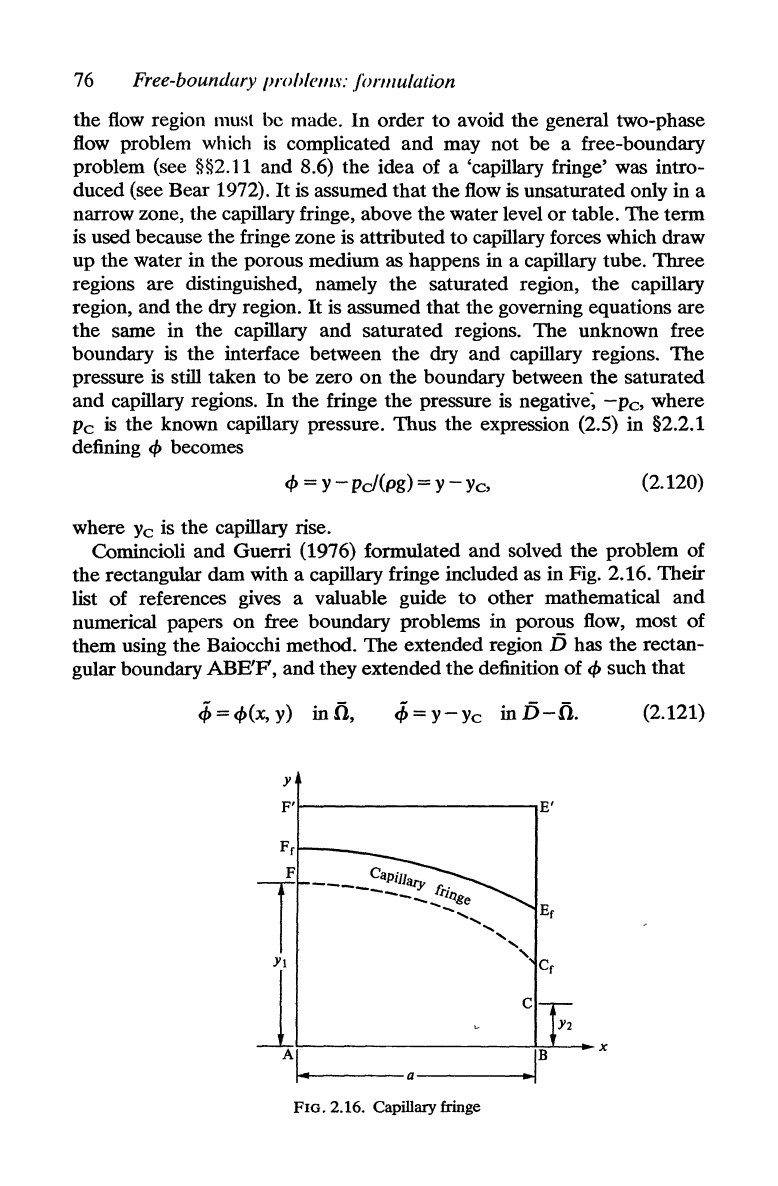
Comincioli and Guerri (1976) formulated

and

solved

the

problem of

the

rectangular dam with a capillary fringe included as in Fig. 2.16.

Their

list

of

references gives a valuable guide

to

other

mathematical

and

numerical papers

on

free boundary problems

in

porous flow, most

of

them using

the

Baiocchi method.

The

extended region

jj

has

the

rectan-

gular boundary

ABE'F,

and

they extended

the

definition

of

cP

such that

<f,

=

cP(x,

y) in ii,

Y

F'I----------.,E'

Frr---

__

F

___

Capillary

---_

IhlJ.L>

.............

oC

-.....

1

YI

..........

"

,

1

A~I~.~~~~~~~~-a------------------~~~~~~x

FIG.

2.16. Capillary fringe

(2.121)

Unsaturated flow: capillary fringe 77

The

Baiocchi variable is defined by

(2.122)

Comincioli

and

Guerri

set out

the

boundary conditions satisfied by

cf>

and

the

derivatives of w(x, y) leading after integration

to

the

following

formulation in terms

of

w(x, y):

w(x,O)=-qx+d

where d=w(O,O), (2. 123a)

w(O,

y)

=!(Y-Yl-Yc?+d-i(Yl

+Yc?,

O=s;y

=S;Yh

(2. 123b)

w(a, y)

=!(y

- Y2-

Yd

2

-qa

+

d-i(Y2+

Yd

2

,

0

=s;y

=S;Y2,

V2w=1

in .0,

w>O

in .0,

V2W=0 in

D-fi,

w=O

in v-n.

(2. 123c)

(2. 123d)

(2. 123e)

(2. 123f)

In

(2.123a)

both

the

flow

rate

q

and

d are unknown

as

also is

s,

the

ordinate of the point

q, in (2.123d). These unknown parameters necessi-

tate

an extension

to

previous methods

of

solution. They reflect

the

fact

that

the

points F

f

,

&,

and

q, are not known.

If

q,

d,

and

s are supposed known, the variational ineqUality

J

Jvw

.

V(v-

w)

dx

dy + J J(v+

-w+)

dx

dy;;oO,

D D

v +

=!(

v + lv\), (2.124)

and

the minimum statement

J(w)=S;J(v),

J(v)

= i J Jlgrad

vl

2

dx

fly

+ J J v+

dx

dy (2.125)

D D

can

be

obtained

and

provide a weak solution of

the

problem

V2w=1,

w>O,

~w=O,

w<O,

O=s;~w=S;l,

w=O,

w=g

onr

D

,.,

(2.126)

where g takes

the

boundary values

of

w specified in (2.123a-d)

and

for .

any fixed

s,

r

N..

signifies

the

boundary lines

FF

and

q,E'

,

rD

.•

=

aD-r

N

••

·

In

the

absence

of

a capillary fringe,

Yc

= 0,

and

we revert

to

the

simple

dam

problem for which (2.124), (2.125),

or

(2.126) can

be

solved by the

Cryer algorithm (8.86).

If

only q is unknown as, for example, in the dam

78

Free-boundary problems: formulation

with a sheetpile (§2.3.2), an extra compatibility condition is introduced

to

obtain

q.

For

-

the

problem with a capillary fringe two compatibility

conditions

were

derived by Comincioli

and

Guerri

(1976)

and

used

to

find

q

and

d for

an

assumed

s.

They

employed a numerical shooting

method

to

find

s.

The

compatibility conditions expressing

the

continuity of

Wx

at

F(O,

Yl)

and

Cr(a, s)

are

derived

by

the

arguments

used

to

obtain (2.57)

in

§2.3.2.

A finite-difference solution is

obtained

on

a grid with mesh sizes

ax

=

hI>

Ay

=

h2

such

that

and

if

w(i,

j)

denotes

the

value

of

w(x, y)

at

the

grid

point

(ihl'

jh

2

),

the

compatibility conditions

are

w(N

a

,

j(s» =

w(N

a

-1,

j(s».

(2.127)

Comincioli (1974)

and

Comincioli

and

Guerri

(1976)

used

the

al-

gorithm described

in

§8.S.1(iii)

t6

introduce

these

compatibility condi-

tions

into

their

basic

SOR

algorithm for

an

assumed value of s which

they

then

improved

by

a shooting

method

based

on

the

physical

boundary

conditions.

Thus

the

equations

and

conditions (2.126)

together

with

the

compati-

bility conditions

(2.127)

are

first solved using So,

an

estimated value

of

s,

to

give a solution

wSo(i,

j).

This solution is examined

on

the

boundary

CE'

(Fig. 2.16).

We

take

Su

==

j(sl)hz, with j

the

smallest integer such

that

j(su);;;:'

N2

and

awSo(N..,

j)/ax > 0

and

apply a heuristic argument

based

on

the

two

boundary

conditions

wx<O

onCCr,

in Fig. 2.16.

Thus

if

and

~

{wSo(N

a

,

j)}

< 0,

ax

we

accept S11 as

the

new estimate

of

s.

If,

however,

we

take

S12

=

j(sdh2'

with j now

the

greatest

integer for which

j(sd

~

Nc

and

a{

wSo(N

a

,

j)}/ay <

-Yc.

Some

interpolated

value

between

Sl1

and

S12 is

then

adopted

as

SI,

the

value

of

s

to

be

used

instead of So in a

second iteration

of

the

SOR

scheme with

the

compatibility conditions.

A generalized dam problem: a new formulation

79

The

process continues till

the

conditions

on

CCr

and

CrE' are simultane-

ously satisfied

by

a solution w(i, j).

2.11.

A

generalized

dam problem: a new formulation

Most

of

the

problems in this chapter, so far, have

been

fonnulated in

terms of

the

Baiocchi variable. In some cases quasi-variational in-

equalities have

been

involved

and

have led

to

mathematical and computa-

tional complications. In efforts

to

circumvent these difficulties, new ap-

proaches, which

are

closely similar

to

each other, were developed inde-

pendently by AIt (1977, 1979, 1980a,b) and Brezis, Kinderlehrer, and

Stampacchia (1978).

The

essence of

the

paper

by

Brezis et al. (1978) is

given in this chapter. AIt (1980) constructed a general-purpose numerical

algorithm

to

solve his new fonnulation

and

this, together with some of his

numerical results,

are

presented in §8.6.

The

dam problem, generalized as in Fig. 2.17, was fonnulated by

Brezis et al. (1978) as follows.

The

symbol S denotes

the

boundary

of

the

dam

and

f

that

of

the

flow region O. Thus S is composed

of

Sh

the

impervious base,

~,

the

parts

of

S in contact with air,

and

S3,

those parts

occupied

by

water.

Thus

S3

coincides with f

3,

while r 1 is

the

wet

part

of

the

base,

Sh

f2

is

the

free boundary,

and

r

4

the

seepage region.

The

pressure p(x, y) satisfies

the

relationships

a

-(p+y)=O

onr

h

av

a

p=-(p+y)=O

onr

2

,

ay

p=</>

onf3'

cf>(x,y)=H(x)-y,

FIG. 2.17. General dam

(2.128)

(2.129)

(2.130)

(2.131)

80

Free-boul/rimy proM/'III,I': .!fll'll/lIlallol/

where

H(x)

is

Iht~

height of the

water

in

a reservoir,

ii

t>

·~O,

-

(p+y)~O

on

f4'

av

(2.132)

because no

water

enters the dam over

the

seepage face. In the rectangular

dam this condition is imposed implicitly, since p

=0

on

f4

and

p>O

in

n.

By the maximum principle, p > 0 on

n,

since

</>;;;.:

0 on r 3 and aplav> 0 on

r

1>

since v

is

always the outward normal.

We

introduce a test function {(x,

y)

which is continuous over the whole

of the dam and its boundaries, i.e. over

D,

and which satisfies { = 0 on r

3,

{;;;.:O

on f

4

•

Then

j j V P . V { dx dy + j j

:;

dx dy

(} (}

=

j

(ap/av+v'y){ds=

r

.i.(p+y){ds~O.

(2.133)

lr4

av

Brezis et

al.

(1978) extended p(x, y) such that p = 0 in D -

nand

introduced the Heaviside function, H, so

that

jjVP'V{dxdY+

jjH(P){ydXd

Y

D D

= j

jvp.

V{

dx

dy+

j j{y dx

dy~O.

(2.134)

(} (}

Since f 4

is

unknown, they put

{=

0 on f 3 =

S3

and

{;;;;oO

on

Sz.

The

problem now becomes

to

find p(x, y) belonging

to

the space of functions

which together with their first derivatives are square summable

on

D,

p;;;;oO

on

D,

and

to find a second function g satisfying

g=l,

p>O,

and

O~g~l,

p=O;

such that

j

jvp.

V{

dx

dy+

j jg{y dx

dy~O

(2.135)

D D

for all { belonging

to

the

same space of functions as

p,

and

{;;;;o

0

on

Sz,

{ = 0

on

S3'

On

Sz

and

~,

p =

</>,

and we

put

</>

= 0 on

Sz·

Brezis et

al.

(1978) established the existence of a unique solution to

the

problem and demonstrated that for a rectangular dam their unique

solution yields a Baiocchi variable

w(x, y) which satisfies the usual

differential inequalities, i.e. conditions (2.35) above.

Visintin (1979) proposed an analogous formulation based on a suitable

Degenerate free-boundary problems

81

extension of the pressure function

and

Quarteroni and Visintin (1980)

studied

the

numerical solution of

the

problem.

2.12. Degenerate free-boundary problems

Generally, a stationary, free-boundary problem of the type considered

so far in this chapter is associated with an elliptic partial differential

equation, whereas in a moving boundary problem the .equation is

parabolic.

There

are, however, some important problems in which the

boundary is moving

but

the

equation is elliptic, i.e. they are degenerate

problems. Examples are provided by the Hele-Shaw flow associated with

the

injection of fluid into a narrow channel and a problem in elec-

trochemical machining. Their formulation

in terms of a variational in-

equality reveals a new feature which can

be

particularly advantageous in

numerical work.

2.12.1. Hele-Shaw

flow

analogy

In

1897, Hele-Shaw devised a cell (see Lamb 1932) consisting essen-

tially

of

two closely spaced glass plates between which

he

studied the

steady-state flow of viscous, incompressible fluids. Recognizing that at

small Reynolds numbers

the

Navier-5tokes equations of motion for his

apparatus

take

the

form of Darcy's law, Hele-Shaw made use of the

mathematical analogy

to

study two-dimensional problems in porous

flow,

particularly ground-water flow around complicated structures.

The

Hele-

Shaw analogy has

been

used by

other

authors

to

study various free-

boundary porous-flow problems (Saffman and Taylor 1958; Taylor and

Saffman 1959; Taylor 1961; Richardson 1972). Saffman

and

Taylor

(1958) were particularly interested in

the

stability of the interface be-

tween

one

fluid and another which is driving it forwards, when penetrating

tongues can form.

In

order

to

examine

the

mathematical analogy more carefully the

situation shown in Fig. 2.18 is considered. The Hele-Shaw flow occurs

u

--------

x

z

FIG. 2.18. Hele-Shaw cell

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.