Crank J. Free and Moving Boundary Problems

262

Fixed-domain methods

TABLE

6.7

Values

of

10

4

C(O,

t)

on the fixed sealed

sUrface

cs

FGL

Time

lix:=

0.01,

t:=

0.001

Iix = 0.05, t = 0.001

HH

0.04

2743

2742

2743

0.06 2236 2234

2236

0.10 1432

1430

1432

0.12

1091

1089

1091

0.14 779

. 777

779

0.16

488

486 488

0.18

218

216

218

0.185

153

151

153

of the

more

general O-type problem (6.153) with suitable extension of the

vector b

to

include all terms in (6.153) of time level n8t.

Elliott (1976) obtained solutions of the oxygen diffusion problem by

using

the

projected

SOR

algorithm (6.137) and (6.138) with zr+l given

by

the

Crank-Nicolson form of

the

left-hand side of (6.132). Some of his

results are included in Tables 6.6-8, where results obtained by other

workers

are

assembled for comparison.

It

is generally accepted that those

of Hansen and Hougaard (1974) are

the

most reliable. Elliott and

Ockendon (1982) presented values of

s(t) obtained by using

the

fast

algorithm (Cottle 1979) described in §8.5 and their values are indicated in

parentheses in Table 6.6.

Other

results for this problem are given in

TABLE

6.8

Values

of

10

4

c(x, t).

At

each time level:

,

top

line

=CS,

8x

=0.05,

8t=0.005; mid-

dle line=FGL,

8x=0.05,

8t=0.001;

bottom

line

=

HH

x

Time

0.1 0.3

0.5

0.7

0.9

0.06

2173

1710

1019

394

41·

2173

1713

1022 396

42

2172

1710

1019

395

41

0.10 1394

1108

659

230

5

1394

1110

661

232 6

1393

1108

659

231

6

0.14

755

571

284

42

754

571

285

42

754

571

284

42

Variational inequalities

263

Tables 3.1, 3.2, 4.1, 4.2, and 6.3.

The

Fourier-series solution of Dahmar-

dab

and Mayers (1983) agrees closely with the values obtained by Hansen

and Hougaard (1974) except in

the

final stages (see §5.1).

6.4.2. Variational fonn

A variational fonn of (6.130) and (6.131) is easily derived by mUltiply-

ing the left-hand side of the first of (6.130) by

(v-c)

using

the

test

functions

v which are non-negative in 0

<x

< 1 with v = 0 on x =

1,

and

for which

v and av/ax are square integrable in 0 < x <

1,

i.e.

J~

v

2

dx and

J~

(av/ax)2

dx are bounded. Thus

1

1(ac a

2

c)

11

ac

---+1

(v-c)dx=

-(v-c)dx

o

at

ax

2

at

-[(v-c)

ac]l

+1

1

ac

~

(v-c)

dx+

I\v-c)

dx.

ax

0

ax

\)

Remembering that v

=c=O,

x = 1, and

ac/ax

=0,

x = o ,'together with use

of (6.131), we obtain after slight rearrangement

1

1 ac 11ac a

-(v-c)dx+

--(v-c)dx

o at .

ax ax

=-1\v-C)dx+1

1

(ac - a

2

c

+l)V

dx.

at

ax

2

But

the

final

tenn

on

the right-hand side of this equation

is

non-negative

since

v;;;;o

0, and

the

first of (6.130)

is

to

be

satisfied. We therefore have

the

variational inequality

eac(v_c)dx+

e

ac

~(V-C)dx;;;;o-1\ti-C)dx.

(6.140)

J

o

at

J

o

ax

Using

the

nomenclature of (6.126) and (6.127),

the

inequality fonnula-

tion of the oxygen diffusion problem (6.140), equivalent

to

the differential

forms (6.130) and (6.131), becomes

(ev

v-c)+a(c,

v-c);;;;o(-l,

v-c).

(6.141)

We

are required

to

find c(x, t) for each t such that (6.141) is satisfied for

all admissible test functions

vex,

t).

A suitable finite-element discretization of

the

variational inequality

(6.141) leads back to the matrix condition (6.133) and hence

to

the

algebraic problem posed by (6.135) and (6.136). This can

be

seen by

considering the slightly more general inequality

(Ut,

v-u)+a(u,

v-u);;;;o(f,

v-u).

(6.142)

264 Fixed-domain methods

Let

both U and the trial functions v be expressed in terms of basis

functions

cf>i

by

N

U = L

Ujcf>i

=

Ujc/>i;

i=1

N

V = L

Vicf>i

=

Vicf>b

i=1

(6.143)

where the suffix convention implying sununation over

all nodes of the

finite element grid

is

used for convenience, and Uj, Vb i = 1,

...

,N,

are the

values at

the

successive nodes.

As

usual,

cf>i

is a basis function associated

with node

i,

which vanishes outside all elements, for example triangular

elements, that have node

i

as

a vertex. For simplicity of explaining the

alternative fonnulation of

the

oxygen diffusion problem, we confine

attention for

the

moment

to

one space dimension so that

the

node i is

conunon

to

only

the

two linear elements

(i-1)h~x~ih

and

ih~x~

(i

+

l)h

in

the

line 0

~

x

~

1 and h =

lIN.

Recalling

the

variational in-

equality (6.142) in

the

expanded

fonn

of (6.140)

and

substituting from

(6.143) we obtain

+ L

Uj-"

L

(Vj_Uj)_i

dx

i

1(N

ac/>i)(

N .

acf»

'=1

aX

i=1

aX

Introducing a mass matrix M;j, a stiffness matrix Kij' and a vector

{;

given

by "

(6. 144a)

"and

noting that M;j and

K;j

are synunetric, we obtain on interchanging i

andj

"

(6.145)

where

the

shorter notation U =

Ujc/>i,

v =

Vic/>i

introduced in (6.143)

is

used.

We

can now use a O-type finite-difference replacement for

aUjlat

and let

uj

denote

the

value of

Uj

at

the

point i = j and time n

8t,

with uj+1 for

the

corresponding value

at

time (n +

1)

8t.

The ineqUality (6.145) becomes

n+l

n

M;j

Uj

8;

Uj

(Vi

-

Uj)+[OK;juj+l+(l-

O)Kijuj](Vi -

Uj)

-fj(Vi

-Uj)~O,

(6.146)

Variational inequalities

265

or

alternatively, on grouping

~erms,

we have

[Mi/St+

eKij]uj+1(Vi

-

ur+l);;;;.[J;

+{Mi/8t-(1-8)K

ii

}uj](vi - ur+

1

).

(6.147)

If

now we take the

cPi

to

be

a set of piecewise linear basis functions

satisfying

_

{{x

-

(i

-l)h}/h,

cPi

- {(i +

l)h

- xl/h.

(i

-l)h:s;x:s;

ih,

ih:s;

x:s;

(i

+ l)h,

(6.148)

and

use the lumped integration familiar in finite-element methods, we

have immediately that

Mii

is

a diagonal matrix with elements

h.

Noting

that

acP/ax=±(l/h) it follows that

Kij

is

tridiagonal with diagonal ele-

ments 2/h and off-diagonal elements -1Ih.

If

now

V(e

multiply both

sides of (6.147) by

at/h,

it takes

the

form

(6.149)

where A

is

a positive definite, tridiagonal matrix with constant diagonal

elements (1

+

2Ae)

and off-diagonal elements -

Ae,

and b =

~

St

-{1-

(1-

e)~i}uj,

where A = St/h

2

•

For f = 1 and e = 1 these A and

b

are

the

same

as

the matriceS in (6.135).

The

solution

is

advanced by

solving

at

each time step the linear complementarity equivalent of (6.149)

by

the

Cryer algorithm of type (6.137), (6.138)

or

otherwise, e.g. for the

oxygen diffusion problem we regain (6.135), (6.136).

6.4.3. Minimization formulation

Finally, we recall that

the

solution of an elliptic partial differential

equation can sometimes

be

expressed as the function for which a certain

integral takes a stationary value, often a minimum value. Correspond-

ingly,

the

solution u of an elliptic variational inequality such as

(u,

v-u)+a(u,

v-u);;;;.(f,

v-u)

is

the

function which minimizes the quadratic expression

J(v) = (v, v) + a(v,

v)-2(f,

v),

provided a(u, v) is symmetric, i.e. a(u, v) = a(v, u). Thus

J(v)-J(u)

= (v, v)

-(u,

u)

+a(v~

v) - a(u,

u)-{2(f,

v)-2{f,

u)}

(6.150)

(6.151)

=

(u-v,

u-v)+2(u,

v-u)+2a(u,

v-u)-2(f,

v-u);;;;.O

if (6.150) is true. Equally,

if

u is known

to

minimize J(v) over a set

of values

of

v for which

(l-p)u+p(v)

is contained in the same set

with

O<p<l,

i.e.

the

set is convex, then immediately

(l/p)

{J«l-p)u+pv)-J(u)};;;;.O

and so

p(v

-u,

v-u)+pa(v-u,

v-u)+2(u,

v-u)+2a(u,

v-

u)-2(f,

v-u);;;;.O.

266

Fixed~domain

methods

In

the limit

as

p

~

0 we regain (6.150). The variational inequality and

the

minimization problem are equivalent.

With this equivalence in mind we return

to

the parabolic inequality

(6.142) and rewrite it in terms of general discrete variables

u;:

and

v;:

of

the type

cdefined

by (6.143)

but

without specifying

the

precise form of the

</Js.

Thus

u;:,

for example, denotes the discrete values of

the

function u at

the nodes of a finite-element mesh of size h

at

time n

St.

The

values of

U;:+l are given by the solutions of a sequence

of.

elliptic variational

inequalities for successive intervals of time

8t,

i.e.

(

U;:+l_

U

;:

""

_u

n

+

1

)

+a(u

n

+

6

n

_u

n

+

1

) >-(jn+6 V

_u

n

+

1

)

8t '

~"

h h

h,

~n

h h

..-

h

,h

h

h,

(6.152)

which can

be

written

as

discrete forms of (6.150) by incorporating

the

term uh/8t with

t;:+fI.

By using

the

discretized version of (6.151), we'see

that (6.152) is equivalent

to

the

problem of minimizing

the

expression

for

all admissible

Vh'

Thus in this formulation

the

oxygen diffusion

problem requires

the

minimization of

the

matrix expression

(6.153)

for

Vi

;;3:0,

where the matrices M and K and

the

vector f are

the

M;.i>

K;.i'

and t of (6.144a) and we regain (6.139) for t =

1,

0 = 1, and

the

A.and

b

M and K

as

in (6.149). '

Lions (1969) and Brezis

(1972a,b) proved that a unique solution of

the

parabolic inequality (6.142) exists. Elliott and Ockendon (1982) estab-

lished that

if

the

weak form, obtained by integrating (6.142) with respect

to

time, i.e.

I

T

[(V"

v,-

u)

+a(u,

v-

u)-(j,

v -

u)]

dt

;;;.:t

Iv(T)-

u(T)12_t

Iv(O)-

Uof,

has a solution in the relevant time-dependent domain, 0

~

t

~

T,

then it

is

a unique solution. They also :.nowell that a unique solution

of

a discrete

form of (6.142), i.e. of (6.152), exists and converges

to

the unique

solution of

the

weak form and hence

to

the

unique solution of (6.142).

Stability criteria .were also established for O-forms of (6.152). Brezis

(1972b), Bensoussan et al. (1975), and Elliott and Ockendon (1982)

established

the

equivalence of

the

differential forms (6.130) and (6.131)

with

the

variational inequality (6.142) and its weak form.

Variational inequalities

267

6.4.4. Review

of

equivalent forms

We

have formulated the oxygen diffusion problem in three apparently

different ways:

(i)

the system of differential equations and inequaltiies

(6.130) and (6.131) and their discrete equivalents (6.135) and (6.136);

(ii)

the parabolic variational inequality (6.141) or (6.142) and the discretized

form (6.152); and

(iii)

the minimization problem of (6.139) and (6.153).

The

latter two forms are alternative statements of a problem in

quadratic programming.

In

that context, the conditions for optimality,

known

as

the Kuhn-Tucker conditions, are in fact

the

algebraic state-

ments (6.135) and (6.136). They arise here from a discretization of the

differential forms (6.130) and (6.131) which constitute a continuous linear

complementarity problem by virtue of the equation (6.131).

We

have

further seen that a linear, finite-element discretization of (6.141) for this

particular problem leads again

to

the

Kuhn-Tucker conditions (6.135)

and (6.136).

Furthermore, Elliott (1976) draws attention to the close connection

between

the

discretized linear complementary problem and the truncation

algorithm of Berger

et

ai.

(1975) discussed in connection with oxygen

diffusion equations (6.117-122) above.

If

we

use

the

8-type discretization

of (6.130) instead of

the

fully implicit form (6.132) we obtain in matrix

notation

(M/~t)(en+l-

en)

+

Ke

n

+

8

+ 1 = z

;;;;'0,

(6.154)

and from (6.131)

the

complementarity condition

(6.155)

Here

K

is

the

usual matrix expression for the finite-difference form of the

second derivative; M

is

a 'diagonal matrix so that in

the

explicit case of

8=0

the

solution

of(6.154)

aIfd (6.155)

is

simply

(6.156)

where F contains

all terms

in'

the

first equality of (6.154) which do not

involve

en+t,

multiplied

by.

&.

Berger et

al.

(1975) also solve

the

first

equation (6.154) and project by (6.156)

to

ensure ci+

1

;;;;.0.

When

8=0,

therefore,

or

whenever M

is

the

diagonal lumped mass matrix, the

truncation method

is identical with the solution of (6.154) and (6.155).

Otherwise Elliott (1976)

and

Elliott and Ockendon (1982) expect trunca-

tion

to

be

less accurate because it does not take account of the com-

plementarityof (6.155). Instead of using the algorithm defined by (6.137)

268~'

Fixed-domain methods

and (6.138), Berger et al. (1975) solve equations like

lit

o

(um+1

2wn+1+

um+1)

h

2

I'Y

.+1

- •

I'Y

.-1

(1-0)

n n n

+

~(Ci-1-2ci

+Ci+1)-1

(6.157)

and then take

The

claim about

the

relative accuracy of

the

two methods is supported by

Elliott's (1976) numerical solution

of

a model problem used by Berger

(1976)

to

test

the

truncation method.

It

is

to

solve

:;=::~+t

0<x<1-t

2

, }

u=O

x=O

1 '

f =

(~Oxt

-20x

~40)e~p(x

+ t

2

-1)-40xt

+44,

(6.158)

and the initial

data

u(x,O) are taken

to

conform with the exact solution

( )

_

{20x{-x-t

2

+exp(x+

t

2

-1)}+

t{I(x),

u

x,

t -

t{I(x),

0~X~1_t2,

1_t2~x~1

where

t{I(x)=2x(1-x).

The

accuracy

is

expressed

at

any time by a

relative

error

Ct:

h{u(ih)

-

u,}2

r

ICt1

1

h{U(ih)}2]! ,

where

U,

are

the

analytic values. These errors tabulated in Tables 6.9,

10 are extracted from fuller tables in Elliott (1976).

The

complementarity values are clearly more accurate than

the

trunca-

tion ones.

The

Crank-Nicolson scheme (0

=t)

appears

to

offer little

TABLE

6.9

Percentage relative

errors

for problem (6.158) obtained by linear com-

plementarity method using projected

SOR

6=1

6=!

Time h = 1/10, 8t = 1/100 h = 1/20,

8t

= 1/400 h = 1/10, 8t = 1/100 h = 1/20,

8t

= 1/400

0.1

0.3

0.5

0.7

0.9

0.072

0.136

0.487

0.134 .

0.023

0.020

0.068

0.025

0.051

0.004

0.231

0.111

0.487

0.081

0.021

0.055

0.062

0.032

0.059

0.003

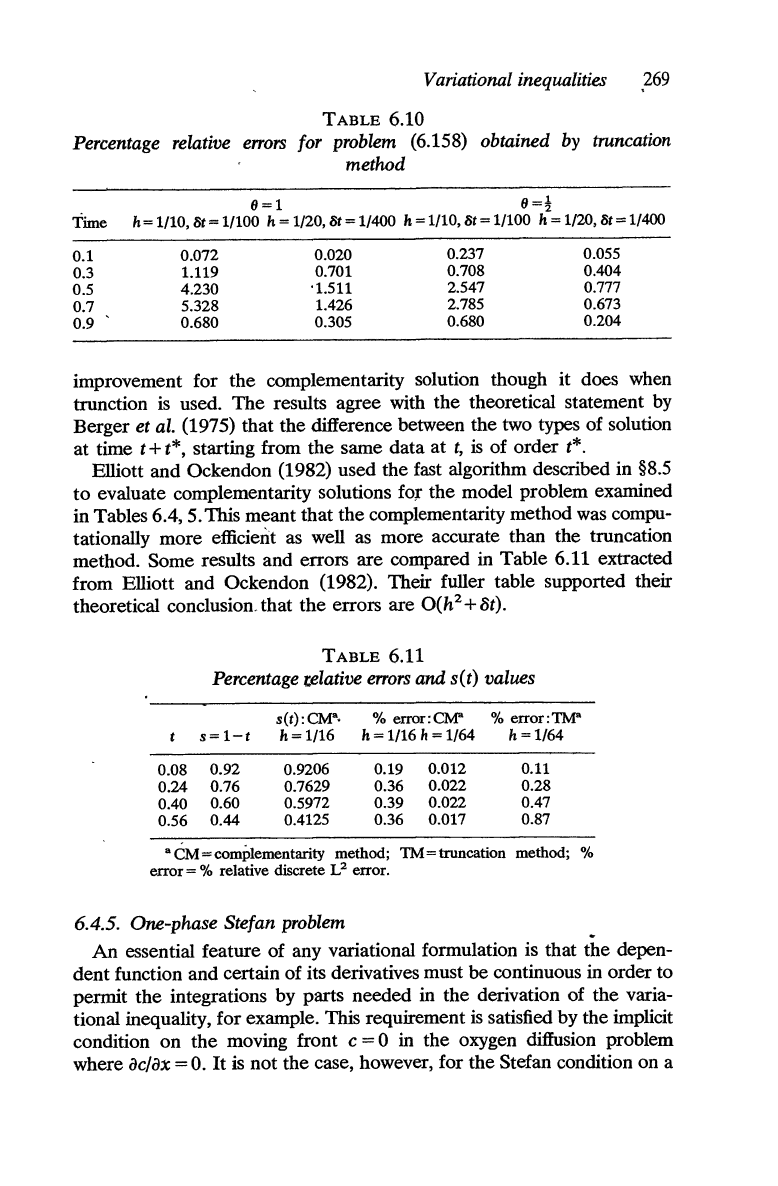
Variational inequalities

269

TABLE

6.10

Percentage relative

errors

for problem (6.158) obtained by truncation

method

Time

0.1

0.3

0.5

0.7

0.9

8=1

8=!

h = 1/10, 8t = 1/100 h = 1/20,

Sf

= 1/400 h = 1/10,

Sf

= 1/100 h = 1/20, 8t = 1/400

0.072

1.119

4.230

5.328

0.680

0.020

0.701

'1.511

1.426

0.305

0.237

0.708

2.547

2.785

0.680

0.055

0.404

0.777

0.673

0.204

improvement for

the

complementarity solution though it does when

trunction

is

used.

The

results agree with

the

theoretical statement by

Berger

et al. (1975) that

the

difference between

the

two types of solution

at time t

+ t*, starting from

the

same data

at

t,

is

of order

t*.

Elliott and Ockendon (1982) used

the

fast algorithm described in §8.5

to

evaluate complementarity solutions for

the

model problem examined

in Tables 6.4, 5. This meant that

the

complementarity method was compu-

tationally more efficient as well as more accurate than the truncation

method. Some results and errors are compared in Table 6.11 extracted

from Elliott and Ockendon (1982). Their fuller table supported their

theoretical conclusion. that

the

errors are

O(h

2

+8t).

TABLE

6.11

Percentage

r,elative

errors and s(t) values

s(t):eM".

% error:

eM"

%

error:TM"

s=l-t

h=1/16

h = 1/16 h = 1/64

h =1/64

0.08

0.92

0.9206

0.19

0.012

0.11

0.24

0.76

0.7629 0.36

0.022

0.28

0.40

0.60

0.5972 0.39 0.022

0.47

0.56

0.44 0.4125

0.36 0.017

0.87

aCM=comPIementarity method; TM=truncation method;

%

error = % relative discrete L2 error.

6.4.5. One-phase Stefan problem

An

essential feature of any variational formulation is that

the

depen-

dent

function and certain of its derivatives must

be

continuous in order to

permit

the

integrations by parts needed in

the

derivation of

the

varia-

tional inequality, for example. This requirement

is

satisfied

by

the implicit

condition on

the

moving front c = 0 in

the

oxygen diffusion problem

where

ac/ax

=

O.

It

is not

the

case, however, for

the

Stefan condition on a

270

Fixed-domain methods

solidification boundary, where the first derivative of temperature

is

dis-

continuous for a non-zero latent heat. A variational formulation

is

only

possible after some suitable transformation has removed the discon-

tinuity. Such a transformation was first proposed by Duvaut

(1973) for

moving boundaries prompted by an idea of Baiocchi (1971) for station-

ary, free boundaries. Fremond

(1974, 1980) called

the

new variable

the

freezing index. Subsequently, theoretical properties have been studied by

Friedman and Kinderlehrer

(1975), Bensoussan and Lions (1978), and

Friedman

(1975).

For

the single-phase melting problem defined by equations (1.21-26),

the

Duvaut transformation,

or

the Fremond freezing index, is

w(x,

t)

=:

It

u(x,

-r)

d-r,

~(x)

O:s;;x

:S;;s(t);

w(x,

t)=O,

(6.159)

where we have introduced the fixed, finite domain

O:s;;

x

:s;;

1,

and where

t =

f(x)

defines

the

time when the ice at point x changes

to

water, i.e.

f(x)

is

the

time when

the

melting boundary

is

at

x.

It

is

the

inverse of

s(t)

so that

rl(t)

= s(t).

To

show that

w(x,

t)

and its first derivative ow/ax are

continuous

on

the

melting boundary and throughout the range

O:s;;

x:s;;

1,

we have from

(6.159) that

oW

11

au

-=

-(.x,-r)d-r,

ax

~(x)

ax

aw=O

ax

'

s(t):s;;x:s;;

1, (6.160)

since the temperature u

is

zero on the interface x =

s(t)

i.e. u(x,

f(x»

= 0,

and from

(6.160) we know that ow/ax = 0 on x = s(t). Furthermore,

<:

a

2

w

It

a

2

u

of

au

-2

=

-2

d-r---

(x,

f(x»,

ax

~(x)

ax ax

ax

O:S;;x<s(t),

(6.161)

since

au/ax=/=

°

on

x

=.s(t),

i.e. at (x,

f(x».

Noting that

of/ax

=

-lI(as/at),

so that

the

Stefan condition (1.26) implies (au/ax){af/ax) =

A,

equation

(6.161) with use of (1.21) becomes

a

2

w 1 t

au

a 1 I

oW

-2=

-d-r-A=-

ud-r-A=--A.

ax

(x)

at at

~(x)

at

Thus the transformed equation

is

oW

a

2

w'

at=

ax

2

+A,

O:S;;x<s(t);

w=O,

with

w(x,

t»O

in'

O:s;;x<s(t).

Thus

w(x,

t)

and its first derivative are

continuous throughout

the

domain

O:s;;

x

:s;;

1 and so

the

inequalities

Variational inequalities

271

corresponding

to

(6.130) and (6.131) are

w;;;.O,

(

a

w

_

a

2

W

-A)W

=0

at

ax

2

'

The

variational inequality

is

now

O,,;;;x,,;;;l,

(W"

v-w)+a(w,

V-W);;;'(A,

V-W),

using

the

nomenclature adopted in (6.141).

(6.163)

(6.164)

(6.165)

. Ichikawa and Kikuchi (1979) formulated a single-phase Stefan problem

in terms of a variational inequality closely similar to

(6.165) but with

application

to

one, two,

or

three space dimensions and with

the

possibility

of three sorts of condition on different segments of the boundary of the

fixed domain, i.e. temperature a prescribed function of time on one

segment, zero temperature on another, and a Neumann

flux condition on

the third segment.

Their problem is defined on an open domain

D with boundary f in

one, two,

or

three space dimensions and a subset a of D is the frozen

region.

On

f G a negative temperature

get)

is prescribed and on f c the

temperature is zero.

On

f F

the

flux is prescribed by a Neumann condi-

tion.

The

time-dependent interface

fo(t)

separates

the

ice and water

regions and

t=S(x).defines

the

time when

the

water changes to ice.

The

formulation of

the

problem is: for given

get),

O,,;;;t,,;;;T,

find

S-l(t)

and

temperature

6(x, t) such that

a6

= V .

(k

V6) in a

at

'

6=0

in

D-a,

6(x, t) =

get)

on f

G,

KV6·

VS(x)=f

on

fo,

6 (x,

0)

= 0 in D.

The

introduction of Duvaut's transformation

a6

016

= K - on f

F,

an

(6.166)

U(x,

t) = r 6(x,

T)

dT

in

a,

S(",)

u(x, t);::O in

D-a,

and

the

reformulation of

the

problem follows precisely

the

derivation of

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.