Crank J. Free and Moving Boundary Problems

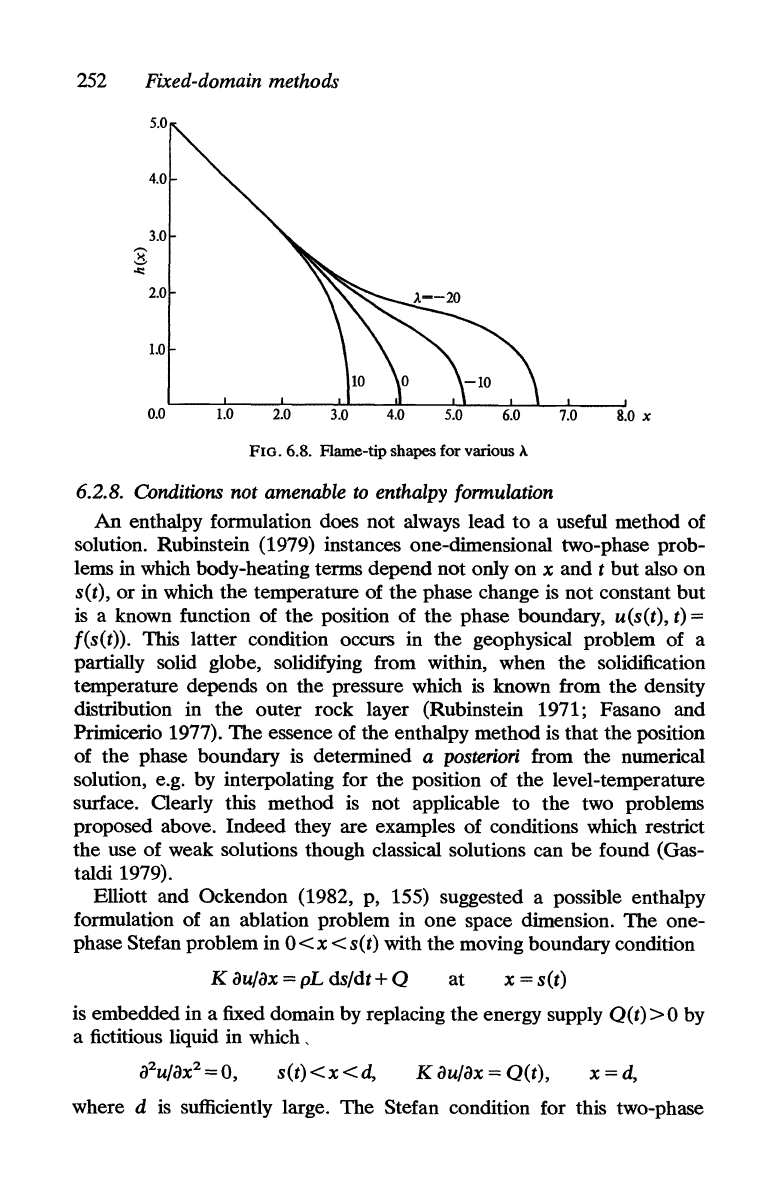
252 Fixed-domain methods

7.0

8.0

x

FIG. 6.8. Flame-tip shapes for various A

6.2.8. Conditions

not

amenable

to

enthalpy formulation

An

enthalpy formulation does not always lead

to

a useful method of

solution. Rubinstein (1979) instances one-dimensional two-phase prob-

lems in which body-heating terms depend not only

on

x and t but also

on

s(t),

or

in which the temperature of the phase change is not constant but

is

a known function of

the

position of

the

phase boundary,

u(s(t),

t) =

f(s(t)). This latter condition occurs in

the

geophysical problem of a

partially solid globe, solidifying from within, when

the

solidification

temperature depends

on

the pressure which

is

known from

the

density

distribution in

the

outer

rock layer (Rubinstein 1971; Fasano and

Primicerio 1977).

The

essence of the enthalpy method is that the position

of the phase boundary is determined

a posteriori from the numerical

solution, e.g. by interpolating for the position of the level-temperature

surface.

Oearly

this method

is

not applicable to the two problems

proposed above. Indeed they are examples of conditions which restrict

the use

of

weak solutions though classical solutions can

be

found (Gas-

taldi 1979).

Elliott and Ockendon (1982, p, 155) suggested a possible enthalpy

formulation of an ablation problem in

one

space dimension. The one-

phase Stefan problem in

O<x

< s(t) with the moving boundary condition

K au/ax = pL

ds/dt+

Q

at

x = s(t)

is embedded in a fixed domain by replacing

the

energy supply

Q(t»O

by

a fictitious liquid in which,

s(t)<x<d,

K au/ax =

Q(t),

x=d,

where d

is

sufficiently large.

The

Stefan condition for this two-phase

Truncation method: alternating phase

253

problem is

[K

aulaxl::;~d=

-pL

ds/dt =

-(K

aUlaX)solid+Q,

because

the

temperature gradient is linear in

the

liquid phase.

Then

an

enthalpy function

H(u)=pcu,

u<O,

H(u)=pL,

u>O

can be used. How-

ever, it is not clear how such a formulation could

be

extended

to

a general

ablation problem in more space dimensions.

6.3. Truncation

method:

alternating

phase

A novel approach

to

moving boundary problems was originated by

J. C. W. Rogers, first in connection with

the

Crank-Gupta oxygen diffu-

sion and consumption problem (see §1.3.10) and later with classical

Stefan problems.

In

the

latter context, the basis of

the

alternating-phase

truncation

(APr)

method of solution is to solve a heat-flow problem in

either

the

liquid

or

the

solid phase alternately in successive time steps.

Precautions are taken

to

ensure

that

energy is conserved.

The

method can conveniently

be

described in terms

of

the

enthalpy

formulation

of

the

one-dimensional Stefan problem (Berger, Ciment, and

Rogers 1979) defined

by

aH=~

(d.

a!l\

H<O,

t>O,

at ax 1

a~

J'

aa~=

a~

(d

w

~!f),

H>>..,

t>O,

H(a,

t) =

F(t),

H(b, t) =

G(t),

H(x,

0) = Ho(x),

t~O,

a<x<b,

H+=>..,

H-=O,

t~O,

aH+

aH-

ds

-dw(O)~+di(O)~=>"

dt'

t>O,

where the enthalpy

H(u)

is given by

u<O}

u~O.

(6.109)

(6.110)

(6.111)

(6.112)

(6.113)

(6.114)

(6.115)

(6.116)

In the above,

>..

is

the

enthalpy jump, C

i

,

Cw

the heat capacities,

and

Ki>

Kw

the

thermal conductivities

of

ice

and

water respectively, with d

i

= Ki/Ci>

dw=Kw/Cw,

F>>",

G<O

are given boundary data, and Ho is the given

254

Fixed-domain

me-thods

initial enthalpy distribution which satisfies

H~A,

a<x<s(O),

and

H",;;;O,

s(O)<x<b.

In

the

discretized problem,

Hi

denotes

the

value of H

at

time t

n

= n 8t

at

the

point Xj = a + j 8x, j = 0, 1,

...

,J.

The

APT

algorithm progresses

the solution from time t

n

to

t

n

+

1

in two separate half-steps.

In

the first

half, sufficient

heat

is added

at

each point of the

soUd

to

convert it

to

liquid.

The

heat equation

is

then solved for the all-liquid region and then

the

heat

that was formerly added

is

subtracted away again.

In

the

second

half-step, enough

heat

to

make

the

liquid region everywhere solid

is

subtracted away,

the

heat

equation in the all-solid region is solved, and

the

subtracted

heat

put

back again. Remembering that H < 0 in

the

solid

and

H>

0 in

the

liquid the

APT

algorithm is:

(i)

Define

Hi

=

max(Hi,

A), j = 0, 1,

...

,J.

This means that in the

solid phase

Hi

= A

at

all points which implies an addition of

heat

to

W in

that

phase; in

the

liquid phase .Hj=Hj.

(ii)

Solve

the

heat

flow problem defined by (6.110, 111) and with

H(b, t) =

A,

starting with

Hi,

0",;;;

j",;;;J

as initial values, by any

suitable finite-difference

or

finite-element method

to

obtain values

of

Hi+!

at t = tn+l .

. (iii) Whatever amounts

of

heat

were added

to

the

Hi

in step (i) are

now subtracted from

the

Hi+!

values

to

obtain

Hi+!,

i.e.

Hi+!

=

Hi+!-

(Hi-

Hi),

j =

1,

...

,J

-1,

and

Ho~

=

F(t

n

),

HJ~

= G(tn).

This is

the

heat-conserving step. The solid phase

is:

now treated

similarly, i.e.

(iv)

Define Hn+! =

min(Hi+!,

0), j = 0,

...

,J,

i.e.

by

appropriate sub-

traction of heat.

(v)

Solve

the

problem defined by (6.109), (6.112) and with H(a, t) = 0,

starting with

Hi+!,

O~j"';;;J

as initial values

at

t=t

n

,

to

obtain

values of

Hi+

1

at

t = tn+l.

(vi)

Whatever amounts of heat were subtracted in step

(iv)

are now

added

to

the

Hi+

1

values

to

obtain

Hi+l,

i.e.

Hj+l

=

Hi+

1

+(Hi+!-Hi:!),

j =

1,

...

, J

-1,

and

H(j+l=

F(t

n

+

1

),

H

J

+

1

=

G(tn+l).

This is

the

second heat-conserving step.

An

advantage of this fixed-domain method

is

that

if

the

heat

parame-

ters are taken

to

be

constant in each phase

the

matrix of

the

simultaneous

equations arising from

the

discretization

is

invariant

and

only one inver-

sion

is

required; advancing

the

solution in time involves only matrix

multiplication. Extension

to

highe! space dimensions

is

straightforward

and solutions relatively easy

to

obtain.

An

illustrative one-dimensional

APT

solution is shown

to

compare favourably with

the

known analytical

solution.

Truncation method: alternating phase

255

An

analytical version

of

the

APT

algorithm for a one-dimensional,

one-phase Stefan problem

is

shown by Berger et al. (1979)

to

have

0([

5t In( 1 +

t/

5t)

1)

rate

of

convergence. Numerical experiments indicate

that

this is a conservative estimate.

Earlier

work

by

Rogers (1977) demonstrated

that

the

oxygen consump-

tion

problem

described in §1.3.10

is

equivalent

to

the

solution

of

a

parabolic

equation

with non-linear absorption

on

a fixed domain. This

work

motivated a fixed-domain numerical method which incorporates

the

use

of

truncation (Berger, Ciment, and Rogers, 1975).

These

authors

reformulated

the

oxygen diffusion problem set

out

in equations (1.57-60)

by considering

the

family

of

non-linear problems

where

ae

a

2

c

at =

ax2-g(c),

0<x<1,

O<t<T,

(6.117)

lim c(x,

t)

= f(x),

0<x<1,

t->O

ac/ax=o,

x=O,

O<t<T,

c = 0 (or ac/ax = 0),

()

{

c/e,

g=g.,c=

1,

x=1,

O<t<T,

O":c":e,

e":c.

(6.118)

(6.119)

(6.120)

(6.121)

There

is

an

associated family

of

solutions ce(x,

t)

and

a function c(x,

t)

=

lime->o

ce(x, t), where c

and

ac/ax

are

continuous functions

of

x and

tin

the

relevant domain,

and

c(x, t) satisfies (6.117-20).

With

g(c)={~:

c=O,

C>O,

(6.122)

the

function c(x, t) satisfies (6.117) almost everywhere

and

is

in fact a

classical solution for which c is everywhere non-negative for

all t. With

f(x) = !(1-

xf

we

have

the

oxygen diffusion problem.

Berger

et

al.

(1975)

established

that

for reasonable physical constants

and

an

absorption

function g(c) defined by (6.121)

or

(6.122),

or

a

third

form

g(c)

=

Vc/(K

+c),

(6.123)

any

standard

numerical

method

of

solution

of

(6.117-20)

on

a fixed

domain could

produce

negative values of concentration c(x, t), unless

the

time

step

were

prohibitively small. This realization motivated their trun-

cation algorithm in which any negative values

that

appear

in

the

numeri-

cal solution

are

set

equal

to

zero after each time step.

Thus,

to

advance

the

numerical solution of (6.117-20) with (6.122), for

example,

to

tR+l,

any standard numerical scheme is used

to

obtain

intermediate solution values,

Wj+1, given

the

numerical solution,

cj,

at

256

Fixed-domain methods

TABLE

6.4

Dependence

of

error

in 10

3

C(X,

t) on At: time

t=0.5

x

tJ.t

0 0.1 0.2

0.3

0.4 0.5

0.05

0

2.23

4.53 6.96 4.84

0.025 0 1.18

2.39

3.65 4.84

0.0125

0 0.594 1.20 1.84 2.52

analytical

solution 107 70.3

40.8 18.7 4.84

o

Finite elements and Crank:-Nicolson in time;

tJ.x

= 0.1;

g(c)""

1.

time

t.

The

values for cj+1 are then obtained by truncating

the

negative

values and taking

(6.124)

at

each grid point j

8x.

The

location

of

the

moving front is taken

to

be

the

position of

the

first zero of

cj+l.

Berger et

al.

(1975) showed satisfactory graphical. results for

the

Crank-Gupta oxygen problem and for a corresponding two-di:rJ;tensional

version. They also examined a similar oxygen consumption problem

but

modified

the

initial and fixed boundary condition so

that

an

analytical

solution' was known. Thus for

c(x,

0)

==

exp(x

-1)

-

x,

the

solution

is

(

)

{

-x-t+exp(x+t-l),

cx,t=

0,

c(O,

t) = e

t

-

t,

x<s(t)

=

1-

t,

x;.o

s(t).

Tables 6.4 and 6.5 show

the

true

solution

at

two different times and

TABLE

6.5

Dependence

of

error

in 10

3

c(x, t) on form

of

g(c) used in truncation

method: time t

= 0.27

x

0

0.1

0.2 0.3

0.4

0.5

0.6

0.7 0.8

g(c) ...

l

0

0.155 0.317 0.493 0.689

0.910

1.16 0.446 0

g(c) from

0

-0.0437

-0.0890

-0.137

-0.187

-0.233 -0.251

-0.446

0

(6.122)

Analytical

solution

212

163

119 80.5 48.9 24.5

8.10 0.446

0

Finite elements and Crank-Nicolson

in

time;

tJ.x

= 0.01,

tJ.t

= 0.006

Variational inequalities

257

errors in numerical results obtained by the truncation method using

g(c)=

1 in Table 6.4 and also g(c) given by equation (6.122) in Table 6.5

which

is

to

be

preferred. Table 6.4 indicates a convergence O(llt)

as

suggested

by

the authors' analysis. Comparisons between truncation

results and linear complementarity solutions are made in

§6.4.4. <

Error

estimates are examined formally by Berger and Falk (1977) for

an explicit truncation method and for an implicit version by Hager

(1980).

Evans and Gourlay (1977) combined the truncation technique

of

Berger et

al.

(1975) with

the

hopscotch scheme due to Gourlay (1970) in

order to solve the oxygen diffusion with consumption problem in a

semi-infinite, two-dimensional domain covered by a finite layer of

another non-consuming material which contains an array of disc elec-

trodes.

6.4. Variational inequalities

Another possibility

is

to formulate moving boundary problems in terms

of certain inequalities, either of a differential

or

variational nature.

In

either case

the

expressions refer to a fixed domain and explicit use of the

Stefan

or

other interface condition is avoided. Both differential and

variational inequalities can lead to numerical algorithms,

but

rigorous

analytical proofs stem mainly from the variational forms. Their dual

usefulness is

one

attractive feature.

One

of

the

earliest publications

on

theoretical properties of variational

inequalities was written by

lions

and Stampacchia (1967). They estab-

lished the existence and uniqueness of the solution of the variational

ineqUality

a(u,

v-u)~(f,

v-u),

(6.125)

defined

as

the function,

u,

for which the ineqUality

is

satisfied for all test

functions

v which satisfy certain conditions.

The

nomenclature with

reference to a domain

D in two space dimensions, for example,

is

that

a(u,v-u)=

JJVU

·V(v-u)dxdy

D

= J

J{Ux(Vx

-Ux)+Uy(Vy -

Uy)}

dx dy

(6.126)

D

and

(f,v-U)=

JJf(V-U)dxdY.

(6.127)

D

258

Fixed-domain methods

Typically,

if

u is

the

solution of an equivalent elliptic partial differential

equation with Dirichlet boundary conditions,

the

functions v will agree

with

u on the boundary aD of

the

domain D and will

be

square

summable together with their first derivatives, which means that

v, v

x

,

vy

exist

on

D and

IS

(V2+V~+

v~)

dx dy

<00.

Depending on

the

problem, v

will

be

bounded above

or

below, e.g.

v;;:;:O

on D.

ay

analogy with

the

classification of partial differential equations,

variational inequalities of this type are termed elliptic. Their applications

to

mechanics and many physical problems are described in

the

book by

Duvaut and Lions (1976). Their application to free-boundary stationary

problems has been developed by Baiocchi and his colleagues, following

an approach introduced by Baiocchi (1971, 1972). This aspect

is

discus-

sed more fully in Chapters 2 and 8 of

the

present book. Good introduc-

tions

and

numerous references are given by Bruch (1980) and by Elliott

and Ockendon (1982).

Moving boundary problems can

be

expressed in terms of variational

inequalities of parabolic type. A general problem can

be

defined in

relation

to

Fig. 6.9, where

S(t)

is

the unknown moving boundary separat-

ing

the

region

n+,

where

the

variable u

is

positive, from

no,

where u is

identically zero.

The

function u satisfying conditions u = 0 in

no,

u =

Un

=

o on

S(t),

u=O

on r

2

,

u=g;;:;:O on

r1>

and u=uo;;:;:O,

t=O

can

be

defined as the solution of

th~

variational inequality ,

(14"

v -

u)+a(u,

v - u);;:;:(f, v -

u)

(6.128)

to

be

satisfied for all test functions v which, as in

the

elliptic inequality

above, are square summable together with their first derivatives and

which satisfy

the

conditions v = g on r

1>

v = 0 on r

2,

and

v;;:;:

(k Lions

(1969) and Brezis

(1972a,b) showed the existence and uniqueness of

the

solution

to

such parabolic inequalities

and

Brezis gave regularity results

for the solution

l.(.

u=g~O

u=u.-O

FIG. 6.9. General domain

Variational inequalities

259

It is easy to confiim that the inequality (6.128)

is

equivalent to the

formulation

u,-v

2

u=f

in

0+,

u=O

in

00,

u =

Un

=0

on

S(t),

u=Uo~O,

t=O,

again with reference

to

Fig. 6.9.

Thu~

(6.129)

(14"

v-

u)+a(u,

v-u)

= f I

u,(v-u)

dx

dy+

f

fvu

.

V(v-u)

dx dy

0+

ri+

= f

I(u,-v2~)(V-U)

dx dy

0+

on

integrating by parts and remembering that v - u = 0 on r 1 and

grad

u

:;:

0 on

S(t).

Hence

('!t,

v-u)+a(u,

v-u)

= f ff(V

-u)

dx

dy~

f

If(V-

u) dx dy

0+

0

which confinns (6.128) provided f is such that

u,-V2u-f~0

in the

whole domain.

We

shall see in §6.4.2 that

the

oxygen consumption problem

is

im-

mediately expressible in terms of a parabolic variational inequality on a

fixed domain.

This is only possible, however; for Stefan problems after a

Baiocchi (1972) type transformation of variable introduced by Duvaut

(1973, 1975) has been applied.

The

new variable

is

continuously differen-

tiable on the whole of a fixed domain and in particular the discontinuity

in the first derivative of tempyrature on the freezing boundary does not

appear in the new variable. Fremond (1974) used the new variable

sometimes referred to

as

the 'freezing index'.

Various moving-boundary problems are formulated

as

parabolic varia-

tional inequalities in the sections that follow, their equivalence to other

formulations

is

established, and their numerical solution is described.

Theoretical aspects are dealt with by Duvaut (1973) for one-phase Stefan

problems, Duvaut (1975) for two phases and by various other authors

including Brezis

(1972a,b), Lions (1969, 1976), Bensoussan, Lions and

Papanicolau (1975), Johnson (1976), Oden and Kikuchi (1978), Aguirre-

Puente and Fremond (1976), and Elliott and Ockendon (1982).

260 Fixed-domain methods

6.4.1. Introductory example

The

oxygen diffusion problem defined by equations (1.57-60) is readily

amenable

to

a variational approach (Baiocchi and Pozzi 1976).

It

is

easy

to

confirm that these equations can

be

combined to give the differential

inequalities

c;;;oO,

(6.130)

together with the equality

(6.131)

The

first of (6.130)

is

satisfied with equality

in

the region

O<x<s(t)

by

virtue of (1.57) and the inequality holds in

s(t)~x~1,

where

c=O,

and

hence the first two teims of (6.130) vanish.

The

second of (6.130) follows

from (1.60) and (1.58) and the fact that c

=0

in s(t)

~

x

~

1.

The

equality

(6.131)

is

true

because

at

every point in

0~x~1

one of

the

factors

vanishes. '

A fully implicit finite-difference form of (6.130)

is

i=

1,

...

,N-1,

(6.132)

where

N 8x = 1 and,

as

usual,

ci

denotes c(i.8x, n

8t)~

The

zero-derivative

condition (1.58) on

x = 0 can be expressed by a centralized difference

or

some other approximation.

The

set of equations (6.132) can

be

expressed

in matrix form

Ac+b;;;oO, (6.133)

where

A is

the

usual tridiagonal matrix with terms 1 + 2,\ on

the

diagonal

and

-,\

as

the

non-diagonal terms, and where b =

8t-cr,

,\ = 8t/(8x)2.

The

n+1_[

n+1

n+1y

Th

hI'

h'

.

(6130)

vector c = Co

,C1

,

•.•

,

CN-1'

e

ot

er

re atlOns

IpS

III

.

and (6.131) give

(6.134)

On

introducing z = Ac +

b,

the

problem becomes that of finding a solution

C

n

+

1

=[c

n

+

1

cn+1

c

n

+

1

Yof

o , 1 ,

.•.

,

N-l

Ac=z-b,

(6.135)

such that

(6.136)

Variational inequalities

261

This is a standard problem in quadratic programming and several well-

known methods exist for its numerical solution.

One

which is amenable

in

the

present context is a generalized successive over-relaxation method

due

to Cryer (1971a). Sequences of vectors

Z(k+l)

and

C(k+l)

are gener-

ated with components given by

i-I

N

Z~k+l)=

b.

+ ' A

..

c~k+l)_'

A'C~k)

t t

i.J

I))

i..J

I1J

j=1

j=i

C~k+l)

=

max{O

C~k)

+

WZ~k+l)/A.}

t

..'

I

I.

It

•

(6.137)

(6.138)

Clearly, without the non-negativity condition in (6.138), corresponding

to

the

so-called complementarity condition in (6.135), this is the standard

SOR

algorithm with relaxation parameter

w.

Cryer (1971a) proved the

convergence of the method for 0

< w < 2 provided the matrix A is positive

definite. More details of this

and

other SOR methods are to

be

found in

§8.5.

An

alternative is the conjugate gradient method (Elliott 1976).

Ichikawa

and

Kikuchi (1979) suggested the use

of

Lagrange multipliers

and

a penalty method. O'Leary (1977) also used

the

conjugate gradient

technique and compared several methods.

The

quadratic programming problem of (6.135) and (6.136) is equival-

ent

to

the

problem

for

C;;;'O,

(6.139)

provided A is symmetric

and

positive definite.

The

Cryer algorithm

therefore provides a solution of

the

minimization formulation (6.139) and

TABLE

6.6

Free

boundary

position

s(t)

cs

a

FGL

b

Time

Sx

= 0.01, St= 0.001

Sx

= 0.05, St = 0.001

HHo

0.04

0.9991

0.9992

0.06

0.9916

0.9918

0.10

0.9325 (9343) 0.9346

0.9350

0.12

0.8790 (8792) 0.8781

0.8792

0.14

0.7986 (7987) 0.7966 0.7989

0.16

0.6830 (6833) 0.6799 0.6834

0.18

0.5011 (5018) 0.4942 0.5011

0.185

0.4333 (4342) 0.4178 0.4334

a

CS

= complementarity solution (Elliott 1976).

b

FGL=

fixed-grid Lagrange method (Crank and Gupta

1972a, b).

eHH

= integral equation solution (Hansen and Hougaard

1974).

Values in parentheses obtained

by

Elliott and Ockendon

(1982) using fast algorithm (Cottle 1979).

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.