Cooper L.N., Feldman D. (Eds.) BCS: 50 Years

Подождите немного. Документ загружается.

August 30, 2010 11:44 World Scientiﬁc Review Volume - 9.75in x 6.5in ch17

High-T

Theory 441

"##$%&'()*+

&'(

(')

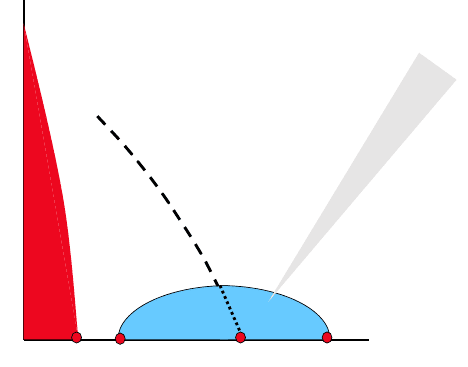
Fig. 1. Typical phase diagram of a hole doped high-T

cuprate superconductor.

AFM = antiferromagnet, SG = spin glass, SC = superconductor, PG = pseudo-

gapped metal, MFL = marginal Fermi liquid, FL = Fermi liquid, gray wedge =

crossover region, red dots = quantum critical points.

lies in the question “What is the mechanism?” Even before the symmetry of

the superconducting order parameter was determined not to be the conven-

tional s-wave, it was understood

that pairing by exchange of phonons as in

traditional superconductors was not the answer. Clues were and are being

sought in the behavior of the two unusual normal states: a “pseudogap”

phase in the low-doping region and a strange metal, or non-Fermi liquid,

phase in the region above the maximum of the superconducting dome. This

region of doping is called “optimal.” For reasons to be discussed below, the

strange metal is labeled MFL, standing for “marginal Fermi liquid,” in the

ﬁgure. In the pseudogap region, a suppression of the density of states near

the Fermi surface is observed. Whether all these are true thermodynamic

phases is still an open question.

In any case, in spite of more than two

decades of theoretical activity, there is as yet no comprehensive theory that

gives all aspects of the unusual behaviors seen in the various regions of the

phase diagram.

The morphology of all the superconducting cuprate compounds involves

CuO

two-dimensional (2D) layers, as depicted in Fig. 2(a). The Cu conﬁg-

uration is 3d

(Cu

) and each oxygen is 2p

2−

). Simple tight-binding

considerations involving the relevant Cu 3d

−y

and O 2p

, 2p

orbitals, as

depicted in the ﬁgure, show that these lead to three planar bands. Since

August 30, 2010 11:44 World Scientiﬁc Review Volume - 9.75in x 6.5in ch17

442 E. Abrahams

(a)

(b)

(c)

Fig. 2. Electronic structure: (a) Structure of CuO

planes. (b) Characteristic

tight-binding band structure for holes. The chemical potential µ is shown for the

half-ﬁlling (undoped) case. (c) Cu and O orbitals giving rise to the bands in (b).

each Cu has one hole in an otherwise full d

−y

band and in the hole-

doped superconductors, extra holes are added chemically, it is convenient to

describe the energy bands in terms of hole states — thus, an antibonding

band dispersing downward, a non-dispersive non-bonding band, and a bond-

ing band dispersing upward, see Fig. 2(b).

In the stoichiometric (undoped, x = 0 in Fig. 1) compounds, the band

arising from the Cu

ions is half full i.e. one hole per site, Fig. 2(b). In view

of the fact that these are insulating antiferromagnets, it is natural to describe

them as Mott insulators.

This is contrary to the conclusion one would get

from band-structure calculations, which all predict the undoped compounds

to be metallic; this is strong evidence that these materials are in the class of

strongly-correlated systems. When divalent strontium is doped onto triva-

lent lanthanum sites in lanthanum cuprate (La

CuO

), for example, to give

2−x

CuO

(LSCO), x extra holes away from half ﬁlling transform the

compound into a metal and, for moderate x, below a transition temperature

August 30, 2010 11:44 World Scientiﬁc Review Volume - 9.75in x 6.5in ch17

High-T

Theory 443

, a superconductor. Thus the superconducting compounds may brieﬂy be

described as two-dimensional doped Mott insulators.

Indeed, in single crystals, all properties are highly anisotropic. For ex-

ample, the typical cuprate tetragonal crystal structure has a c/a ratio of

almost ﬁve (in lanthanum cuprate) and in the normal state of the super-

conducting compounds the measured resistivities are in the ratio ρ

/ρ

at least 10 and usually with opposite temperature dependences. Thus the

physics, hence the observed magnetism and superconductivity, is dominated

by the CuO

planes common to all the cuprates.

The phase diagram of Fig. 1 depicts the situation when extra holes are

doped into the CuO

planes. There is also the class of electron-doped

cuprates, such as Nd

2−x

CuO

(NCCO). The phase diagram for electron-

doped materials usually shows the same main phases as the hole doped

superconductors, but with a number of diﬀerences, principally a broader

antiferromagnetic region. Research on the properties of electron doped com-

pounds, while extensive,

is not yet as comprehensive as that on the hole

doped cuprates. Taking the point of view that the experimental diﬀerences

between the two classes do not signify that there is a basic divergence in

the underlying physics, we concentrate in what follows on the hole-doped

case.

There are three main families of the hole-doped high-T

superconduc-

tors. They diﬀer in the number per unit cell of CuO

planes, the manner of

doping away from a parent antiferromagnetic insulator and the presence or

absence of chains between the planes. There is the single-plane lanthanum

cuprate family (LSCO) mentioned above; the two-plane compounds based on

YbBa

7−x

(YBCO) where holes are introduced by oxygen deﬁciency;

and the compounds with diﬀerent number of planes composed of bismuth,

strontium, copper, oxygen and with or without calcium (BSCCO).

This combination of low dimensionality and strong-correlation Mott

physics led Anderson

and others to suggest that fundamentally new

physical ideas are required to explain the behavior of the cuprates, which

is sketched in Fig. 1. Probably the “simplest” eﬀective Hamiltonian for a

strongly-correlated system is the one-band Hubbard model (see Eq. (2)).

But what is the essential reduced Hamiltonian for the cuprates as doped

Mott insulators? If we restrict our attention to the CuO

planes, then

only the Cu

−y

and the O

2−

, 2p

orbitals are relevant, as shown

in Fig. 2(c). An extended Hubbard model can capture both the insulat-

ing antiferromagnet of the undoped compound and the metallic character

when extra holes are doped into the planes. Such a Hamiltonian reads

August 30, 2010 11:44 World Scientiﬁc Review Volume - 9.75in x 6.5in ch17

444 E. Abrahams

(in electron notation)

V SA

= −

hijiσ

iσ

jσ

+ h.c.) + U

j↑

j↓

+ V

hiji

+ ∆

− m

), (1)

where d

creates an electron in a Cu d

−y

2 orbital on Cu site i, p

destroys

an electron in a p

or p

orbital on an O site j and n or m counts the

number of electrons in the relevant Cu or O orbitals. The ﬁrst term is the

kinetic energy due to electrons hopping between nearest neighbor Cu and

O ions, the second is the short-range Hubbard repulsion on Cu, the third

is the Coulomb repulsion between electrons on nearest neighbor sites and

the last is the local ionic energy diﬀerence (∆ = E

− E

) between O and

Cu (shown in Fig. 2(b)). The phases of this extended Hubbard model were

discussed by Zaanen, Sawatzky and Allen (ZSA).

They showed that when

U is very large and ∆ suﬃciently exceeds t

, a hole in the Cu d

orbital

becomes localized and an insulating state is formed with ∆ playing the role

that U plays in the simple one-band Hubbard model; then the charge gap

in this case is the energy to transfer the hole from Cu to O, rather than U.

There is still no consensus about how much of this Hamiltonian is essential

for the cuprates. Further reduction would lead to a simple one-band Hubbard

model on a square lattice

= −

hijiσ

t(d

iσ

jσ

+ h.c.) + U

j↑

j↓

(2)

This is the eﬀective Hamiltonian proposed by Anderson

and it must be said

that it has been adopted in the majority of theoretical works on cuprate

superconductivity. What happened to the oxygens? There are at least two

points of view. One is that in view of the analysis of ZSA, the only essential

thing for the behavior of the cuprates is holes hopping on a square lattice

with strong on-site repulsion. The other is that a doped hole (beyond the

undoped half-ﬁlled case) forms a mobile spin singlet complex that involves

the four oxygens neighboring a copper and the original copper hole, the so-

called Zhang-Rice singlet.

This leads, if the energy scales are appropriate,

to an eﬀective one-band model. The applicability of the Zhang-Rice picture

depends on ∆ > t

, which may or may not be true, depending in part on

what renormalizations are to be included in the deﬁnition of ∆. For example,

the early density-functional calculations,

which included e.g. all the static

August 30, 2010 11:44 World Scientiﬁc Review Volume - 9.75in x 6.5in ch17

High-T

Theory 445

renormalizations due to U and V give a ∆ close to zero. On the other hand,

the experimental fact is that the undoped compounds are antiferromagnetic

insulators; according to ZSA this means that ∆ > t

, apparently justifying

the Zhang-Rice picture.

The analysis of Zhang and Rice

leads ﬁnally to an eﬀective one-band

Hamiltonian that involves only d electrons:

t−J

= −

hijiσ

t(1 − n

i,−σ

iσ

jσ

(1 − n

j,−σ

) + J

hiji

· S

−n

/4], (3)

where J = (2V

/∆

)[1 + 2∆/U]. Here the kinetic energy term contains pro-

jections that prevent double occupancy. This is identical to the t −J Hamil-

tonian

derived in the large U limit from the one-band Hubbard model H

in 2D. In that case, J = 4t

/U. One sees immediately from Eq. (3) that

at half-ﬁlling, where n

= 1, one is left with the 2D Heisenberg antiferro-

magnet whose ground state is now known to be the usual two-sublattice

N´eel antiferromagnet. The values of the parameters in the t −J model that

are appropriate for a typical cuprate

are t ∼ 0.4 eV, J ∼ 0.13 eV. This

corresponds to U ∼ 12t ∼ 4.8 eV for the original one-band Hubbard model.

As shown in Fig. 1, three main phases of the typical cuprate supercon-

ductor are tuned by doping and temperature. They are the normal (i.e. non-

superconducting) strange-metal (region of optimal doping) and the pseudo-

gap (“underdoped” region) states and the superconducting state itself. In

a complete theory of the high-T

materials, all of the regions of the phase

diagram are to be understood, as well as the crossovers between them. This

is a stronger demand on a theoretical framework than that faced by Bardeen,

Cooper and Schrieﬀer and their reduced Hamiltonian. The conventional su-

perconductors of 1957 are much less complex than the cuprates; only two

phases were at play. For the high-T

materials, it will be much more diﬃcult

to replicate the fantastic success of BCS theory, which not only accounted

for all the observed properties of superconductors, but also predicted others.

There have been a number of reviews of theoretical treatments of high-

temperature superconductivity.

16–19

A list of some of the theory ideas and

techniques that have been developed in connection with high-T

makes clear

how diﬃcult it might be to give a comprehensive survey:

Spin ﬂuctuations, anisotropic phonons, excitons, charge

ﬂuctuations, plasmons, circulating currents, bipolarons,

resonating valence bonds, stripes, interlayer tunneling,

spin bags, spin liquids, ﬂux phases, BCS-BEC crossover,

August 30, 2010 11:44 World Scientiﬁc Review Volume - 9.75in x 6.5in ch17

446 E. Abrahams

marginal Fermi liquid, van Hove singularities, quantum

criticality, anyons, time reversal violation, dynamical

mean ﬁeld theory, slave bosons, gauge theory, d-density

waves, gossamer superconductivity, SO(5), . . .

Rather than a duplication of some earlier overviews, what follows here con-

sists instead of short descriptions of some of the ideas that are important for

historical background and/or are representative of current research.

3. RVB and Gauge Theories

Perhaps the earliest systematic attempts to describe the phases of the

cuprates were carried out using the Hubbard model Eq. (2) in the limit

of inﬁnite U, that is to say with the constraint that double occupancy of any

site is forbidden. This may be realized in a variety of ways. Since most of

this topic has been extensively reviewed by Lee, Nagaosa and Wen,

only a

brief summary is given here.

A variational method can be built with the use of a Gutzwiller projec-

tion,

(1 − n

i↑

i↓

) operating on a trial wave function, for example

the BCS wave function, which does not contain the eﬀects of strong repul-

sion. This was applied by Anderson

in his formulation of the resonating

valence bond (“RVB”) description of the 2D lightly-doped Hubbard model

(near one-electron per site). The importance and consequences of the pro-

jection have been continually emphasized by him and the method has been

used frequently since Ref. 21. Anderson’s RVB state arises because of the

eﬀective exchange interaction (e.g. from the t − J model) that can give an-

tiferromagnetism in the Mott insulating state at half-ﬁlling. At half-ﬁlling,

the Cu spins-1/2 are localized and the antiferromagnetic exchange interac-

tions between them can generate a spin-liquid state of ﬂuctuating singlet

pairs (RVB), which because of the eﬀect of quantum ﬂuctuations on the

long-range ordered two-dimensional spin-1/2 N´eel state can be nearby in

energy to the latter. This RVB spin-liquid state has only short-range an-

tiferromagnetic correlations and it has spin 1/2 fermionic excitations called

spinons. This is in contrast to the antiferromagnetic state, which has S = 1

excitations. The RVB state is thought to be stabilized by the addition of

holes, which destroys the N´eel state. This picture has attractive features that

we will mention below in connection with the properties of the underdoped

(pseudogap) region of the phase diagram.

As an alternative to the Gutzwiller projection, some subsequent devel-

opments have been based on the recognition that the leading eﬀect of very

August 30, 2010 11:44 World Scientiﬁc Review Volume - 9.75in x 6.5in ch17

High-T

Theory 447

strong short-range repulsion (as in the Hubbard model) can be captured by

a constraint which keeps electrons of antiparallel spin apart. Thus, no more

than one electron per site (“no-double-occupancy”). The approach then

requires a treatment of the constraint with weak residual interactions

arising from deviations from the strong coupling limit. In leading order,

this is the content of the t − J model [Eq. (3)].

At half ﬁlling, one electron per site, n

= 1, the kinetic energy drops

out of the t − J Hamiltonian and one is left with a (localized) spin only

Heisenberg antiferromagnet. The metallic phases of the t − J model occur

when it is doped away from half-ﬁlling, e.g. by adding x holes, as in the hole-

doped cuprate superconductors. The motion of holes under the constraint

of no double occupancy leads to a long-range retarded interaction which is

mediated by a dynamical gauge ﬁeld with substantial low-energy weight.

This interaction, arising solely from the constraint, is ultimately responsible

for the low-temperature anomalies and non-Fermi liquid behavior in the

normal-state properties of the model.

To understand the origin of this gauge ﬁeld, we begin by examining the

constraint n

iσ

≤ 1. It is convenient to replace the inequality

with an equality for each site. This is achieved by regarding each site as

being occupied by either a spin-up fermion, a spin-down fermion (spinons,

iσ

) or by a spinless boson representing a hole (holon, b

). This is done

by expressing the original electrons as d

iσ

= f

iσ

. The constraint is then

+ b

b = 1, which explicitly eliminates double occupancy of any

site from the Hilbert space. In the case of the Hubbard model, it has been

shown

that a mean ﬁeld treatment using the slave boson method is explic-

itly connected to the Gutzwiller approach of projected wave functions. The

approach invites non-Fermi liquid behavior at the outset via the replace-

ment of the physical electrons by the spinon-holon composite objects and

it is a mathematical realization of the spin-charge separation that is char-

acteristic of excitations in RVB theory and in one-dimensional interacting

electron systems. There is still the possibility that the spinons can behave

as a Fermi liquid. This occurs, for example, when the holons undergo Bose

condensation, their dynamics then drops out of the problem.

Typically, the t − J Hamiltonian is rewritten in terms of these new op-

erators and mean-ﬁeld solutions to the problem are obtained as usual by

decoupling the interaction terms.

t−J

→ −t

hijiσ

iσ

jσ

−

hijiσσ

iσ

jσ

iσ

. (4)

August 30, 2010 11:44 World Scientiﬁc Review Volume - 9.75in x 6.5in ch17

448 E. Abrahams





















Fig. 3. Mean-ﬁeld phase diagram of the slave-boson treatment of the t − J model.

The constraints are generated with the use of Lagrange multipliers that

modify the action, which deﬁnes the quantum statistical mechanical parti-

tion function. At the simplest mean-ﬁeld level, these are taken to be all

equal. That is, the constraint is taken globally rather than being satisﬁed

at each site.

There were several successes of this simple slave-boson approach. Most

prominently, although postulated one or two years earlier by a number of

workers, “unconventional” d-wave superconductivity, later conﬁrmed experi-

mentally, was predicted in a slave boson calculation in 1988.

Although the

antiferromagnet at half ﬁlling is not captured, the various mean-ﬁeld treat-

ments lead to a number of phases that are suggestive of the experimentally

observed behavior. These are sketched in Fig. 3.

17,25

The reader should not

fail to notice similarities between Figs. 1 and 3. The interpretation here is

that below the “RVB line,” the spinon bond operator

iσ

jσ

acquires

a nonzero expectation value χ

6= 0 and a uniform singlet RVB state be-

gins to form, leading to a spin gap. The pseudogap then arises from the

energy required to break singlets. This is reﬂected in the magnetic suscepti-

bility, speciﬁc heat and, in particular, in the conductivity perpendicular to

the CuO

planes. Other parts of the phase diagram are generated in mean

ﬁeld by holon Bose condensation hbi 6= 0 (red line in the ﬁgure), and d-wave

spinon pair condensation hf

i↑

j↓

−f

i↓

j↑

i 6= 0 (blue line in the ﬁgure). When

both order parameters are nonzero, long range order of d-wave superconduc-

tivity is obtained in a dome-shaped region of the phase diagram, just as in

the actual materials.

August 30, 2010 11:44 World Scientiﬁc Review Volume - 9.75in x 6.5in ch17

High-T

Theory 449

It was soon recognized that these mean-ﬁeld approximations inadequately

represent the inﬂuence of the constraints, insofar as the latter are obeyed only

on average. Consideration of ﬂuctuations around the mean-ﬁeld solutions

leads to gauge theory. Speciﬁcally, the average version of the constraint

is realized by the saddle point value of the Lagrange multiplier referred to

above. Its ﬂuctuations represent the time component of a U(1) gauge ﬁeld

whose spatial components are represented by the phase of the spinon bond

ﬁeld χ

. The spinons and holons couple to the gauge ﬁeld and the result is

in essence a strong-coupling problem. Further elaboration of the approach

is described extensively in the review of Lee, Nagaosa and Wen.

We have seen that the slave-boson approach to the t −J model can serve

as a microscopic basis for RVB states and spin-charge separation. A mean-

ﬁeld treatment gives a phase diagram that contains much of what is seen

experimentally in the hole-doped cuprates. However, a number of diﬃculties

presented themselves as the U(1) gauge theory was developed. One is that

the predicted behavior of the superﬂuid density as the doping is decreased

was at odds with the experimental results. This led to further elaboration

of the gauge theory approach to include the SU(2) symmetry appropriate

to the undoped situation. This is described in detail in Ref. 17. In spite of

such diﬃculties and the mathematical complexities of further development,

the general philosophy of RVB as a basis for the understanding of cuprate

superconductors retains substantial adherents.

It is important to note that the RVB and gauge theory developments

described in this section are all based on enforcing the constraint of no

double occupancy, that is to say the limit of inﬁnite Hubbard repulsion U.

The issue of the diﬀerence between inﬁnite and ﬁnite U is not often discussed.

The question is whether the physics of a moderate U system in which some

double occupancy may occur, can be well-captured in the inﬁnite U limit.

In this connection, it should be mentioned that the proposal of gossamer

superconductivity

rests on a partial Gutzwiller projection, which permits

superconductivity (perhaps with extremely low superﬂuid density) to coexist

with antiferromagnetism in the state that is insulating at inﬁnite U . This

shows that there can be profound diﬀerences between the two regimes.

4. Phenomenologies

The complexities of the cuprates and the rapid proliferation and reﬁne-

ment of experimental techniques have often determined the direction of

theoretical activity. It is fair to say that absent a complete theory of the

August 30, 2010 11:44 World Scientiﬁc Review Volume - 9.75in x 6.5in ch17

450 E. Abrahams

high-temperature superconductors, these eﬀorts were essentially phenomeno-

logically based. In the late 1980s, high transition temperatures, pairing

mechanisms and symmetry of the superconducting order parameter were

focus issues.

4.1. Spin ﬂuctuations

In the ﬁrst decade of the high-T

era, spin ﬂuctuation theories for the super-

conducting transition were prominent. The motivation was the proximity

of the antiferromagnetism, evidence for antiferromagnetic spin ﬂuctuations

from neutron scattering and nuclear magnetic resonance studies, and the

successes of a related approach for the understanding of unconventional

superconductivity in the heavy fermion compounds. Superconductivity

would arise because of pairing mediated by the spin ﬂuctuations, analogous

to phonon-mediated pairing in conventional BCS superconductivity. Unlike

the heavy fermions, which have spin degrees of freedom that are not directly

associated with the conduction electrons, spin ﬂuctuations in the cuprates

are made from the same electrons that provide the charge carriers that con-

dense into the superconducting state. Thus a phenomenological construction

of “spin-fermion” models, in which conduction electrons are coupled to spin

ﬂuctuations that are consistent with the frequency and wave number sus-

ceptibility observed in neutron scattering. The origin of such a coupling, is

of course the Coulomb interaction, which is repulsive. However, the spatial

structure of the antiferromagnetic spin ﬂuctuations favors opposite spins on

neighboring sites; this conspires to give an eﬀective pair attraction provided

the pair wave function is in the d-wave angular momentum channel. This

was another prediction of d-wave superconductivity in addition to the one

mentioned above.

This phenomenological approach, while it lacks a microscopic derivation,

has been used to calculate various properties of the superconducting and

normal states, with mixed success. Reviews of the problems and successes

of this phenomenology are available in several places.

19,28

4.2. Marginal Fermi liquid

Besides the remarkable high transition temperatures of the copper oxide

metals, it soon became apparent that the normal state properties were

not those of ordinary Fermi-liquid-like metals. In particular, in the doping

region of the maximum T

, near the top of the superconducting dome seen

in the phase diagram of Fig. 1, virtually every normal state thermodynamic