Cooper L.N., Feldman D. (Eds.) BCS: 50 Years
Подождите немного. Документ загружается.

August 25, 2010 14:12 World Scientific Review Volume - 9.75in x 6.5in divider
IV. BCS Beyond
Superconductivity

This page is intentionally left blank

September 17, 2010 9:45 World Scientific Review Volume - 9.75in x 6.5in ch18
THE SUPERFLUID PHASES OF LIQUID
3
He: BCS THEORY
A. J. Leggett
Department of Physics, University of Illinois at Urbana-Champaign,
1110 West Green Street, Urbana, IL 61801, USA
aleggett@illinois.edu
Following the success of the original BCS theory as applied to superconduc-
tivity in metals, it was suggested that the phenomenon of Cooper pairing
might also occur in liquid 3-He, though unlike the metallic case the pairs
would most likely form in an anisotropic state, and would then lead in this
neutral system to superfluidity. However, what had not been anticipated
was the richness of the phenomena which would be revealed by the experi-
ments of 1972. In the first place, even in a zero magnetic field there is not
one but two superfluid phases, and the explanation of this involves ideas
concerning “spin fluctuation feedback” which have no obvious analog in
metals. Secondly, the anisotropic nature of the pair wave function, which
in the case of the B phase is quite subtle, and the fact that the orientation
must be the same for all the pairs, leads to a number of qualitatively new
effects, in particular to a spectacular amplification of ultra-weak interac-
tions seen most dramatically in the NMR behavior. In this chapter I review
the application of BCS theory to superfluid 3-He with emphasis on these
novel features.
As is well known, the element helium is unique in remaining in the liquid
state under its own vapor pressure down to (apparently) zero temperature,
freezing only at a pressure of the order of 30 atm; this is true of both the
stable isotopic species,
4
He and
3
He, although their freezing pressures are
somewhat different. In the case of the heavy (and more common) isotope,
4
He, it has been known since 1938 that at a temperature of approximately
2.2 K (at saturated vapor pressure) the liquid makes a transition to an exotic
phase (He-II) in which it shows behavior qualitatively different from that of
a normal liquid, including most spectacularly the ability to flow through
narrow capillaries with zero viscosity, the phenomenon that was christened
by Kapitza “superfluidity”; thus the He-II phase is usually known informally
473
September 17, 2010 9:45 World Scientific Review Volume - 9.75in x 6.5in ch18
474 A. J. Leggett
as “superfluid
4
He”. Following the original proposal of Fritz London, the
modern understanding of the superfluid phase is based on the idea that this
phase is characterized by the phenomenon of Bose–Einstein condensation
(BEC), in which a nonzero fraction of all the atoms (which since Z = 2 and
A = 4 are bosons) occupy a single one-particle state. This hypothesis leads
to a very satisfactory qualitative and sometimes even quantitative picture of
the properties of the superfluid phase of
4
He, see e.g. Ref. 1.
In the case of the light (and rare) isotope,
3
He, no evidence of super-
fluidity or any other exotic behavior is found above temperatures of the
order of 3 mK; indeed, above this temperature liquid
3
He appears to behave
qualitatively like any other liquid. However, quantitatively the behavior,
particularly below ∼100 mK, is rather unique among liquids; for example,
the specific heat is approximately linear in temperature, and the spin sus-
ceptibility is temperature-independent. A qualitative understanding of this
behavior may be obtained from the consideration that, since the
3
He atom
contains two electrons with total spin zero and a nucleus with spin 1/2,
it may be regarded as a composite spin-1/2 fermion and hence should obey
Fermi statistics. If one considers a gas of noninteracting Fermi particles with
the mass and density (at s.v.p.) of liquid
3
He, then the Fermi temperature
should be of order 5 K; thus, at temperatures well below this, the parti-
cles should constitute a degenerate Fermi gas, similarly to the electrons in a
normal metal, and thus should display the characteristic behavior of such a
system. Of course, there are some important differences with the electrons
in a normal metal: the
3
He atom is electrically neutral, so the interatomic
forces are short-ranged rather than the r
−1
Coulomb interaction, there is no
background lattice and no immediate analog of the electron-phonon interac-
tion or of impurity scattering. One result of this latter circumstance is that
the transport coefficients in normal liquid
3
He are limited only by atom-atom
collisions, the frequency of which is, because of the Pauli principle, propor-
tional to T
2
; thus the viscosity and spin diffusivity are proportional to T
−2
,
while the thermal conductivity (thermal diffusivity times specific heat) is
proportional to T
−1
. In addition, while the temperature-dependences of
quantities like the specific heat and spin susceptibility of liquid
3
He are in-
deed those expected for a degenerate noninteracting Fermi gas, the absolute
values are rather different. This is not surprising, given that the system
is nothing like a noninteracting gas; in fact, the mean interatomic distance
(∼4
˚
A) is not much greater than the hard-core radius (∼2 · 6
˚
A); what is
at first sight surprising is that the Fermi-gas picture gives even qualitative
agreement with the data.
September 17, 2010 9:45 World Scientific Review Volume - 9.75in x 6.5in ch18
The Superfluid Phases of Liquid
3
He: BCS Theory 475
Major insight into the reasons for this behavior came from the “Fermi-
liquid” approach of Landau, published in 1956. Rather than starting from
the noninteracting Fermi gas and trying to calculate the effects of the inter-
actions quantitatively, Landau in some sense turned the problem around and
asked: suppose we make the explicit assumption that perturbation theory
in the interaction will eventually converge, then what conclusions can we
draw about the groundstate and low-lying excitations of the strongly inter-
acting system (the “Fermi liquid”)? He showed that under that assumption
there would be a one-one correspondence between the low-lying states of the
noninteracting gas and the (fermionic) low-lying states of the Fermi liquid,
so that one can parametrize the latter by the same quantum numbers as
the former, namely the deviation δn(p, σ) of the number of particles with
momentum p and spin σ from its value (θ(p − p
F
) where p
F
is the Fermi
momentum) in the groundstate. In the interacting system one may think
intuitively of δn(p, σ) as the deviation from its groundstate value of the
number of “quasiparticles”, a quasiparticle being a real atom surrounded by
a “dressing cloud” of other atoms. Landau was further able to show that
when the Hamiltonian is expressed in terms of the quantities δn(p, σ) there
are only two differences from that of the noninteracting gas: first, the disper-
sion relation (p) and hence the effective mass m
∗
≡ p
F
/(d/dp)
p=p
F
would
be modified from the mass m of a free
3
He atom, and secondly, there would
arise various interaction terms that, thanks to the symmetry of the situa-
tion, can be expressed in the form of a set of “molecular fields,” of which
the simplest to visualize are the “Hartree” field arising from a variation in
total density and the “Weiss” field generated by a spin polarization. In the
Landau Fermi-liquid approach the strengths of the various molecular fields,
like the effective mass renormalization, are not supposed to be calculated
but have to be inferred from the experimental data. Consequently, in the
first few years following Landau’s 1956 paper, there was some scepticism
among those working on liquid
3
He that this approach was anything more
than a parametrization of the data; however, such doubts were eventually
put to rest by the observation of a novel collective excitation (“zero sound”)
predicted by the theory, and of some anomalous effects in the spin-diffusion
behavior in high magnetic fields, where one could account for a wide range
of behavior at the cost of only one new fitted molecular-field parameter. By
1972 most of those working on liquid
3
He were convinced of the nontriviality
and utility of the Fermi-liquid theory; indeed it had proved consistent with
just about all the experimental behavior of this system. In the meantime,
Silin and others had shown that a variant of the theory could be applied to

September 17, 2010 9:45 World Scientific Review Volume - 9.75in x 6.5in ch18
476 A. J. Leggett
the electrons in normal (nonsuperconducting) metals, again explaining the
previously rather mysterious success of a simple Bloch–Sommerfeld model
(a model that takes into account crystalline band-structure effects but not,
except in a simple mean-field way, the effects of the strong Coulomb inter-
action) in accounting at least qualitatively for the experimental behavior.
Following the publication in 1957 of the BCS theory of superconductivity
and its rapid acceptance by the community, people soon started to ask: if the
normal state of liquid
3
He resembles so relatively closely that of the electrons
in a normal metal, could the phenomenon of Cooper pairing not occur also in
that system? Should this indeed occur, then since the
3
He atom is electrically
neutral, the resulting state would clearly not be superconducting; however,
it might be expected to show the analog of superconductivity in a neutral
system, namely superfluidity (as in liquid
4
He); consequently, the possible
Cooper-paired state of
3
He, at that time hypothetical, became informally
known as “superfluid
3
He”. In the years between 1958 and 1972 a substantial
amount of theoretical work was done on the possible superfluid phase [sic!]
of liquid
3
He, and a number of important results were established that have
stood the test of time. First, it very soon became evident that the structure
of any Cooper pairs formed in that system was likely to be rather different
from that postulated in the original BCS theory of superconductivity. To
discuss this question, let us define the two-particle order parameter
F (rr
0
σσ
0
) ≡ hψ
†
σ
(r)ψ
†
σ
0
(r
0
)i (1)
where the angular brackets have their usual significance in BCS theory of an
“anomalous average,” i.e. strictly speaking, if one insists on particle number
conservation, the “average” should be understoood as a matrix element of
the bracketed combination of operators between many-body states differing
by 2 in the total particle number N. The quantity F is fundamental in
BCS theory; its physical significance is that it is the unique eigenfunction
of the two-particle reduced density matrix associated with a macroscopic
O(N)
eigenvalue, multiplied by the square root of that eigenvalue (N
0
);
so, apart from the factor of
√
N
0
, it can be thought of as the “wave function
of the Cooper pairs”. (For more details, see e.g. Ref. 2, Sec. 5.4.) The
more commonly encountered Ginzburg–Landau “order parameter” Ψ(R) is,
in the simple case considered by BCS, the special case of (1) corresponding
to r = r
0
≡ R, σ = −σ. Let us for the moment assume that the center
of mass of the pairs is at rest, so that F is a function only of the relative
coordinate, which as there should be no danger of confusion we will simply
call r.

September 17, 2010 9:45 World Scientific Review Volume - 9.75in x 6.5in ch18
The Superfluid Phases of Liquid
3
He: BCS Theory 477
In the original BCS theory, the spin state of the pairs is a singlet and can
be factorized out, so that (in an obvious notation)
F (r, σσ
0
) =
1
√
2
(↑↓ − ↓↑) F (r) (2)
Moreover, if with BCS we ignore the rather annoying but inessential
complications due to the presence of a crystal lattice, F (r) is taken to be
simply a function of r ≡ |r| (“s-wave state”), so that the internal structure
of the pairs is completely isotropic in both spin and orbital space. Since the
form of the function F (r) is fixed, at any given temperature and pressure,
uniquely by the energetics, there are no degrees of freedom associated with
this internal structure.
It was soon realized in thinking about the possibility of formation of pairs
in liquid
3
He that their relative wave function is unlikely to be of a similar
form. The reason is the following: the Fourier transform of F (r), F (k), is
according to the BCS theory given by ∆/2E
k
, where ∆ is the energy gap and
E
k
≡
p
(
k
− µ)
2
+ |∆|
2
, with µ the chemical potential; ∆ is proportional to
the transition temperature T
c
, which both in a typical (pre-1986) supercon-
ductor and in liquid
3
He is known from experiment to be at most of order
10
−3
times the Fermi energy (which is essentially µ). Thus, the real-space
pair wave function F (r) is made up of a “packet” of (relative) plane waves
with the magnitude of their k-vectors approximately k
F
(≡ p
F
/~). If this
packet is isotropic (s-wave) as in the BCS theory, then at short distances
F (r) is approximately proportional to sin(k
F
r)/(k
F
r), so that the probabil-
ity to find the two fermions of the pair at a relative distance . k
−1
F
(∼1
˚
A
−1
for both metals and
3
He) is approximately some nonzero constant. For the
case of a typical metallic superconductor this state of affairs is tolerable and
indeed desirable, since at such short distances the phonon-induced indirect
interaction is attractive and the direct Coulomb interaction, while repulsive,
is too “soft” to make much difference. However, for the case of liquid
3
He
there is a very strong hard-core interatomic repulsion, due primarily to the
Pauli principle, at distances ∼k
−1
F
, so that pairs formed in a relative s-state
are likely to have a positive energy with respect to the normal state.
Thus, it was soon concluded that should Cooper pairs indeed form in
liquid
3
He, they were likely to do so in a state of relative angular momen-
tum higher than zero (it can be shown that in the limit ∆ E
F
the relative
angular momentum is approximately a good quantum number, i.e. the quan-
tity F (r) must be composed of spherical harmonics Y
lm
of the same l-value
(but possibly different m-values, see below). For the moment, we ignore the
spin degree of freedom). In such a case, the probability density to be at
September 17, 2010 9:45 World Scientific Review Volume - 9.75in x 6.5in ch18
478 A. J. Leggett
relative distance r vanishes at the origin and has its first maximum near
the point r
l
≡ l/k
F
. Now the attractive part of the van der Waals poten-
tial between two
3
He atoms is maximum around 3
˚
A, and the closest r
l
to
this corresponds to l = 2, so most of the early papers concluded that this
angular momentum was the most likely to occur (“d-wave pairing”). Evi-
dently, by the Pauli principle, such a state would have to be a spin singlet,
so the spin wave function factors out just as in the original BCS theory. In
an important early paper, Anderson and Morel
3
gave a detailed analysis of
this possibility, concluding that the pairs would most likely form not with a
single value of m but in a combination that minimized the gap anisotropy
and thus that of the pair wave function F (r) (it turns out that in the case
of l 6= 0 spin singlet pairing the angular anisotropy of the energy gap ∆(k)
over the Fermi surface approximately tracks that of F (k) and thus of the
real-space function F (r)). Anderson and Morel also gave a brief discussion
of the case of l = 1 (p-wave) spin triplet pairing; in this case, they chose to
investigate one specific possible state, in which the “up” and “down” spins
form pairs independently but with a common direction of relative angular
momentum L. As we shall see below, this was a serendipitous choice.
A few other theoretical developments in the period before 1972 are worth
mentioning. First, while early papers, including that of Anderson and Morel,
had assumed that in the case of spin triplet pairing “up” spins paired only
with up and “down” with down, it was pointed out by Vdovin
4
and inde-
pendently by Balian and Werthamer
5
that it is possible to form a state in
which, in addition, some up spins are paired with down (this is discussed in
more detail below) and moreover that at least in the case of p-wave (l = 1)
pairing the resulting state (which has become known in the literature as the
BW state) would have, within a standard BCS-like approach, a lower energy
than the kind of state considered by Anderson and Morel. Secondly, it was
shown
6,7
that one could combine the ideas of BCS on pairing in a weakly
interacting Fermi gas with those of Landau on a strongly interacting normal
Fermi liquid to produce a theory of a “superfluid Fermi liquid”; interest-
ingly, the molecular fields introduced in Landau’s approach, which in the
normal phase merely renormalize various constants, can in the superfluid
state change the predicted temperature-dependences appreciably. Thirdly,
it was pointed out
8
that in a Fermi system that is nearly ferromagnetic (as
is, at least arguably, the case in liquid
3
He where the enhancement of the
free-gas susceptibility by the relevant molecular field is about a factor of 4)
there would be, in addition to any “bare” forces such as the van der Waals
interaction, an extra interaction, analogous to the phonon-mediated interac-
September 17, 2010 9:45 World Scientific Review Volume - 9.75in x 6.5in ch18
The Superfluid Phases of Liquid
3
He: BCS Theory 479
tion in a BCS superconductor, due to the exchange of virtual long-lived spin
fluctuations, which would be repulsive in a spin singlet state but attractive
in a triplet one.
Thus, in the spring of 1972 the general opinion in the community inter-
ested in liquid
3
He could probably have been summarized as follows:
1. It is quite likely that Cooper pairs will form at some temperature
(only the braver souls among the theorists ventured to predict at
what temperature, and their estimates ranged over 15 orders of mag-
nitude);
2. If pairs form, they will probably form in a d-state but possibly (be-
cause of the effect of the spin-fluctuation-exchange interaction) in a
spin triplet (p- or f-) state;
3. If the pair state is p-wave, it will be the BW state;
4. The most obvious diagnostic of the onset of Cooper pairing will be
superfluidity, plus a BCS-like jump in the specific heat at the tran-
sition to the paired phase and a decrease in the spin susceptibility
below the transition.
In the event, Nature had some surprises in store for us. In the late
fall of 1971, Doug Osheroff, at the time, a graduate student in the group
of David Lee at Cornell, was measuring the pressurization (P versus T )
curve of a mixture of solid and liquid
3
He at temperatures below 3 mK. He
observed two tiny but reproducible anomalies in the curve, which we now
recognize as signaling, respectively, a second-order transition to one new
phase (now known as the A phase) and a first-order transition between that
phase and a second new phase (the B phase). Subsequently, yet a third new
phase (the A
1
phase) was found to occur in high magnetic fields. Evidently,
“superfluid
3
He” is a richer system than the theorists had anticipated! The
phase diagram of liquid
3
He below 3 mK in zero magnetic field as we now
know it is shown in Fig. 1.
What is the nature of these new phases? Although the earliest exper-
iments did not give direct evidence for superfluidity (this came somewhat
later) most of the community rapidly concluded that all three new phases
were indeed Cooper-paired phases analogous to the superconducting phase
of metals. But what was the symmetry (internal structure) of the pair wave
function in each case (A, B, A
1
)? To discuss this question, we need to
introduce a little standard notation.
Let us consider, as above, the pair wave function F (r, r
0
, σ, σ
0
) and for the
moment set the dependence on the center-of-mass variable R ≡ (r + r
0
)/2 to
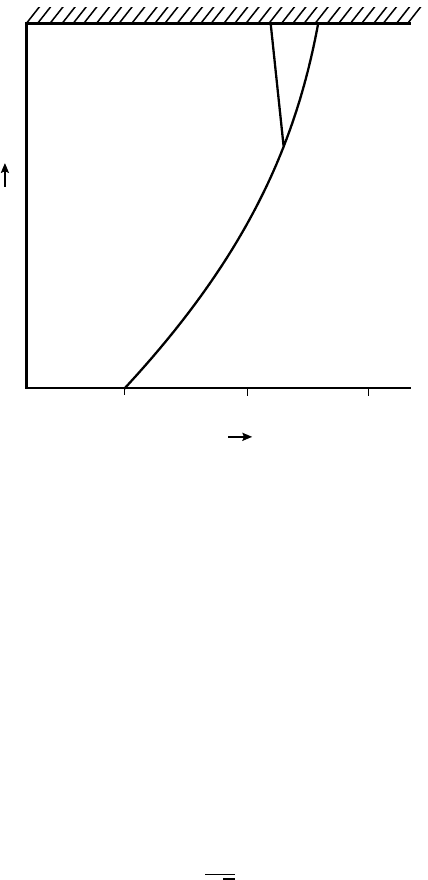
September 17, 2010 9:45 World Scientific Review Volume - 9.75in x 6.5in ch18
480 A. J. Leggett
Solid He
3
P (atm)
T (mK)
B
A
N
1
2
3
Fig. 1. Phase diagram of
3
He in zero magnetic field.
be a constant. Then, changing notation so that r now denotes the relative
coordinate (formerly r −r
0
) we can write quite generally
F = F (r, σ, σ
0
) (3)
According to the Pauli principle, if F is a singlet (triplet) in spin space it
must be an even (odd) function of r, and it turns out that except under rather
pathological conditions it is energetically disadvantageous to mix these two
possibilities, so we can discuss them separately. In the case of singlet pairing
(which turns out not to be directly relevant to superfluid
3
He) the spin
function factors out just as in the original BCS theory, i.e. we can write in
an obvious notation
F = F (r) ·
1
√
2
(↑↓ − ↓↑) (4)
What is the general structure of the orbital wave function F (r)? In
the original BCS theory it is isotropic and as a function of |r| looks much
like the wave function of two free atoms at the Fermi surface up to a
distance of the order of a characteristic length ξ ∼ ~v
F
/k
B
T
c
(the “pair
radius,” or within a factor of order unity, the “Pippard coherence length”),
but beyond that point falls off as exp −|r|/ξ, indicating that the two-particle
