Cooper L.N., Feldman D. (Eds.) BCS: 50 Years

Подождите немного. Документ загружается.

August 24, 2010 17:25 World Scientiﬁc Review Volume - 9.75in x 6.5in ch12

Superconductor-Insulator Transitions 261

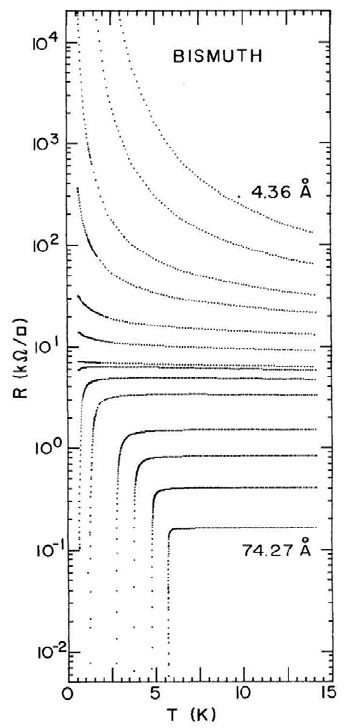
Fig. 2. Evolution of the temperature dependence of the sheet resistance R(T ) with

thickness for an a-Bi ﬁlm deposited onto Ge. Fewer than half of the traces actually

acquired are shown. Film thicknesses that are shown range from 4.36 to 74.27

(From Ref. 31.)

a phenomenon treated theoretically by Smith et al.

The energy gap also

vanishes on the insulating side of the SI transition of homogeneously dis-

ordered ﬁlms,

and on the insulating side of the ﬁeld-tuned transition.

These studies suggest that there are serious amplitude ﬂuctuations associ-

ated with the SI transition. One might also conclude from this interpretation

that the vanishing of the energy gap implies that the amplitude of the order

parameter vanishes in the insulating state, which would appear to falsify the

August 24, 2010 17:25 World Scientiﬁc Review Volume - 9.75in x 6.5in ch12

262 A. M. Goldman

Boson-localization model. Such a conclusion should be treated with care as

the vanishing of the gap feature in superconducting tunneling could result

from other eﬀects such as pair breaking by phase ﬂuctuations.

4. Scaling Analysis of the Critical Regime of a Continuous SI

Transition

Because the SI transition is so intimately connected with the idea of direct

continuous quantum phase transitions, it is of interest to examine this in

more detail. As mentioned, the application of the quantum phase transition

(QPT) paradigm followed the publication of the data of Fig. 2. Contin-

uous QPTs are transitions at absolute zero brought about by changing a

parameter in the Hamiltonian of the system.

1,58

The quantum mechani-

cal ground state changes when the critical point is crossed. In contrast

with phase transitions at nonzero temperature, quantum eﬀects are central

to QPTs. In other phase transitions, although the order parameter itself

may be quantum mechanical, classical thermal order parameter ﬂuctuations

govern its behavior at the relevant long wavelengths. In the case of QPTs,

the ﬂuctuations themselves are quantum mechanical. Near a QPT there are

divergent correlation lengths, for the spatial, ξ, and temporal, ξ

, directions.

The latter is associated with a vanishing energy scale. These lengths depend

on the control parameter, δ = |(g − g

)/g

for the transition. Here g can be

a measure of disorder, magnetic ﬁeld, or charge, and g

is the critical value

of the control parameter. We then write:

ξ ∼ |δ|

−ν

, and ξ

∼ ξ

(1)

This deﬁnes the correlation length exponent ν and the dynamical critical

exponent z, where ξ and ξ

are the correlation length and dynamical cor-

relation length, respectively. Physical quantities in the critical region close

to the QPT are homogeneous functions of the independent variables in the

problem. Details of issues relevant to quantum phase transitions are consid-

ered in the works cited above.

The key feature of QPTs is the interplay of dynamics and thermody-

namics. As a consequence of this, a d-dimensional quantum system at ﬁnite

temperature is described in the T → 0 limit as a classical system of d + z

dimensions, with the ﬁnite extent of the system in the extra dimensions

being given by −~β in units of time, where β = 1/k

T . The extent of these

extra dimensions are divergent only in T → 0 limit. What is remarkable

is that the universality class of the quantum transition may be one studied

extensively in some classical context. This also allows for the possibility of a

August 24, 2010 17:25 World Scientiﬁc Review Volume - 9.75in x 6.5in ch12

Superconductor-Insulator Transitions 263

computational treatment of the quantum mechanical problem using simula-

tions of the d + z dimensional classical problem. Disorder on the other hand

can change the universality class of the equivalent classical problem. It is

also not true in general that space and time enter in the same fashion in the

equivalent classical problem. For this to happen the dynamical exponent, z,

must be unity, and whether or not this happens depends upon the detailed

quantum dynamics of the system.

As mentioned above, the eﬀect of considering T 6= 0 in the statistical

mechanics is to force the “temporal” dimension of the problem to be ﬁnite.

The formal model used to analyze data at nonzero temperatures is ﬁnite-

size scaling. The success of ﬁnite size scaling analyses of the various

superconductor-insulator transitions is part of the evidence for there being

QPTs. Scaling can be used to characterize properties measured at nonzero

temperatures in the regime of critical ﬂuctuations and thus to determine the

critical exponents and universality class of the transition. For the resistance

near the transition, it is of the form:

R = R

F (δ/T

1/υz

, δ/E

1/υ(z+1)

) (2)

Here R is the sheet resistance, R

and F are an arbitrary constant and an

arbitrary function. The energy scale for the ﬂuctuation Ω ∼ ξ

−z

is cut

oﬀ at nonzero temperature by k

T , deﬁning a cut oﬀ length L

given by

T ∼ L

−z

. This gives rise to the ﬁrst term in the argument of the arbitrary

function F . The second term comes from a characteristic length associated

with the electric ﬁeld as compared with the correlation length. The ap-

plicability of these ideas assumes that there is a continuous and direct SI

transition. Hebard and Palaanen carried out the ﬁrst scaling analysis of a

perpendicular ﬁeld driven transition of In

ﬁlms.

They found that the

exponent product, νz ∼ 1.2 from scaling with only the ﬁrst argument of

Eq. (2). Later Yazdani and Kapitulnik analyzed the properties of Mo

ﬁlms, carrying out both temperature and electric ﬁeld scaling.

They re-

ported both νz and ν(z + 1) and thus ascertain that z = 1 in agreement

with expectations for systems with long-range Coulomb interactions.

For homogeneous ﬁlms of diﬀerent types, including cuprates, there are

numerous ﬁnite-size scaling analyses of experimental data for the perpendic-

ular ﬁeld-driven transition in addition to the work of Hebard and Paalanen

and Yazdani and Kapitulnik. These include Paalanen, Hebard, and Ruel,

Okuma and Kokubo,

Inoue et al.,

Seidler, Rosenbaum and Veal,

Wang

et al.,

Okuna, Terashima and Kokubo,

Gantmakher et al.,

and on the

thickness and ﬁeld-driven transitions together, Markovic et al.

43,44

These

are all consistent with a quantum critical point. An important caveat is

August 24, 2010 17:25 World Scientiﬁc Review Volume - 9.75in x 6.5in ch12

264 A. M. Goldman

that the success of scaling by itself and the identiﬁcation of the univer-

sality class of the transition from the values of the critical exponents may

not elucidate the microscopic physics of the transition or the nature of the

insulating state.

5. Scaling of Continuous Quantum Phase Transitions

We now consider data of R(T, δ) for a set of ﬁlms diﬀerent from those shown

in Fig. 2. As is typical of such experiments, at some critical thickness, d

, R

becomes temperature independent, while for even thicker ﬁlms it decreases

rapidly with decreasing temperature, indicating the onset of superconduc-

tivity. The critical thickness is found by plotting R versus d at diﬀerent

temperatures (inset of Fig. 3) and identifying the crossing point for which

the resistance is temperature independent, or by plotting dR/dT versus d

at the lowest temperatures and ﬁnding the thickness for which dR/dT → 0.

In the quantum critical regime the resistance of a two-dimensional system is

expected to obey the scaling law of Eq. (2), with the in-plane electric ﬁeld

taken to be a constant.

To analyze the data, we obtain curves of R(d) at various temperatures.

Having determined the critical thickness in the manner described above, we

then rewrite Eq. (2) as R(t, δ) = R

F (δt) where t = T

−1/υz

, and treat the

parameter t(T ) as an unknown variable which is determined at each temper-

ature to obtain the best collapse of the data. Speciﬁcally, t is determined by

performing a numerical minimization between a curve at a particular tem-

perature and the lowest temperature curve. The exponent product υz is then

found from the temperature dependence of t, which must be a power law in

temperature for the procedure to make physical sense. This procedure does

not require detailed knowledge of the functional form of the temperature

or thickness dependence of R, or prior knowledge of the critical exponents.

A diﬀerent method of obtaining critical exponents was also used to check

the consistency of this procedure. A log-log plot of (∂R/∂d)|

versus T

−1

was constructed. Its slope is equal to 1/νz if Eq. (2) is obeyed. Exponents

obtained this way were essentially identical, within the quoted experimental

uncertainty, to those obtained using the ﬁrst procedure.

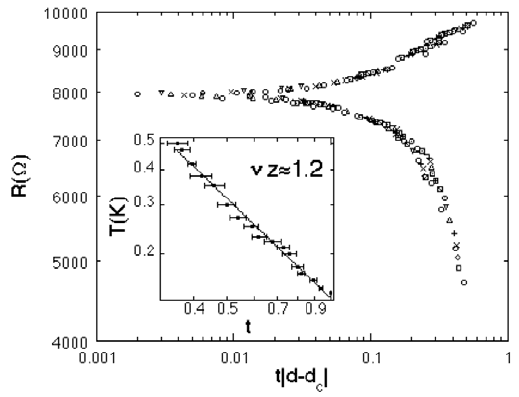
The collapse of the data of R(T, δ) is shown in Fig. 3.

The exponent-

product υz is found to be 1.2±0.2, with the error determined from the power

law ﬁt. This agrees with theoretical predictions from which z = 1 would be

expected for a bosonic system with long-range Coulomb interactions inde-

pendent of dimensionality, and with ν > 1 in 2D.

August 24, 2010 17:25 World Scientiﬁc Review Volume - 9.75in x 6.5in ch12

Superconductor-Insulator Transitions 265

Fig. 3. Resistance per square as a function of the scaling variable, t|d − d

|, for

17 diﬀerent temperatures, ranging from 0.14 to 0.5 K. Diﬀerent symbols represent

diﬀerent temperatures. Inset: temperature dependence of t. (From Ref. 44.)

When the exponent product was determined with magnetic ﬁeld rather

than thickness as the tuning parameter, νz = 0.7 ± 0.2 was found. The

fact that the ﬁeld-tuned transition diﬀers from the thickness-tuned transi-

tion suggests a universality class diﬀerent from that of the thickness-tuned

transition. If z = 1, this result, with ν ∼ 0.7, would correspond to the 3D

XY model.

It is important to note several features of these two SI transitions. The

transitions are direct in that there appear to be no intermediate metallic

phases and there is no resistance saturation at the lowest temperatures. This

is in contrast with results reported for other types of systems

11,66

or what

was found in granular ﬁlms.

It should also be noted that the ﬁlms, which

have been studied in the case of the perpendicular ﬁeld-tuned SI transition

are very close in their properties to the insulating regime. Subsequent works,

in our laboratory on a-Bi ﬁlms,

and by others on a-Pb ﬁlms,

which were

less disordered have revealed the presence of an intermediate regime that

may have two phases. The precise nature of the phase diagram is not known

at this time.

Parker et al.,

also explored the SI transition by decorating Pb ﬁlms

with magnetic impurities. They did not carry out a scaling analysis of this

data.

August 24, 2010 17:25 World Scientiﬁc Review Volume - 9.75in x 6.5in ch12

266 A. M. Goldman

Fig. 4. Resistance versus temperature at various values of ∆n for the 10.22

A thick

ﬁlm with B = 0. Data are shown from 60 mK to 1 K. The values of ∆n that are

shown, from top to bottom, are 0, 0.62, 1.13, 1.43, 1.61, 1.83, 2.04, 2.37, 2.63, and

3.35

1013 cm

−2

. 44 curves of R(T ) for other values of ∆n are omitted from the plot

for clarity. Inset: slope of ln(T ) versus ∆n in the normal state. (From Ref. 19.)

The superconductor-insulator transition of a-Bi ﬁlms has been studied

in parallel magnetic ﬁelds with two types of samples, those in which super-

conductivity was induced by electrostatic doping, which will be discussed

below, and those which were intrinsic superconductors with thicknesses close

to the critical thickness for the appearance of superconductivity.

In both

instances exponent products of about 0.7 were found.

The SI transition has also been tuned electrostatically. This gets around

issue of sample inhomogeneity and vortex pinning that are important in

thickness and perpendicular magnetic ﬁeld tuned transitions. In this ap-

proach the level of physical disorder is in principle ﬁxed, and the outcome is

not dependent upon the degree of vortex pinning.

The ﬁeld eﬀect geometry was one in which SrTiO

(STO) crystal served

as both a substrate and gate insulator. A sequence of a-Bi ﬁlms was stud-

ied.

19,69

The temperature dependence of insulating ﬁlms was governed by

the 2D Mott variable range hopping form.

The addition of electrons to a 10.22

A thick ﬁlm, using the ﬁeld eﬀect,

induced superconductivity as shown in Fig. 4. An important ﬁnding in this

work was the crossover from 2D Mott hopping in the insulating regime to

a ln(T ) dependence of the conductance on temperature in the normal state

for ﬁlms which underwent a transition to superconductivity. What was also

August 24, 2010 17:25 World Scientiﬁc Review Volume - 9.75in x 6.5in ch12

Superconductor-Insulator Transitions 267

found is that the coeﬃcient of the ln(T ) term in the conductance was a

linear function of the charge transfer, as shown in the inset to Fig. 4. This

coeﬃcient is related to the screening of the electron–electron interaction.

This SI transition was successfully analyzed using ﬁnite-size scaling, em-

ploying the charge transfer ∆n as the control parameter. This suggests that

the electrostatically tuned transition is also a continuous quantum phase

transition. In this instance, the exponent product νz was 0.7 ± 0.1, includ-

ing data all the way up to 1 K if the ln(T ) dependence of the conductance

was ﬁrst removed. This was done by assuming that there were two parallel

conductance channels, one involving weak localization and electron–electron

interactions, and the other the critical ﬂuctuations.

The apparent coincidence of an insulator-metal transition with the insu-

lator superconductor transition suggests that the charge-tuned SI transition

is an electronic phenomenon and is not associated with the localization of

bosons.

6. Metallic Regimes

Measurements by Mason and Kapitulnik,

Chervenak and Valles,

Qin

et al.,

and Seo et al.,

support the idea of a metallic regime for certain

samples. Gantmakher and collaborators

reported a similar behavior. The

resistances of ﬁlms, which have dropped signiﬁcantly at high temperatures

and appear to be superconducting, were found to saturate at nonzero values

in the T → 0 limit. This metallic regime, between the superconductor and

insulator, exhibits a resistance much lower than that of the normal state.

Chevernak and Valles

in their ﬁeld-tuned studies refer to this phase as

a vortex liquid. Tewari has suggested that this is a sharp crossover that

appears to be ﬁrst order in character from a strong superconductor to an

inhomogeneous state, which is a weak superconductor.

Kapitulnik et al. discussed the possibility that coupling to a dissipative

heat bath characterized by a single parameter stabilizes the metallic phase.

Dissipation also plays a diﬀerent role in phase-only theories of the SI tran-

sition of granular superconductors that build on the physics of resistively

shunted Josephson junction arrays.

Dissipation can localize the phase of

the system, leading to superconductivity.

Mason and Kapitulnik reported

that a ground plane in proximity with a MoGe ﬁlm seems to promote

superconductivity, although it did not change the dynamical critical ex-

ponent as might be expected with enhanced screening.

Vishwanath et al.,

have presented a comprehensive theoretical discussion of screening and

August 24, 2010 17:25 World Scientiﬁc Review Volume - 9.75in x 6.5in ch12

268 A. M. Goldman

dissipation. In their work, a ground plane introduces screening of the long-

range Coulomb interaction and provides a source of dissipation due to the

gapless diﬀusive electrons.

Work on hot electron eﬀects in the parallel ﬁeld

transition, suggested that resistance saturation may be the result of a failure

of electrons to cool.

This work also casts doubt on the validity of electric

ﬁeld scaling as discussed in Yazdani and Kapitulnik.

In studies of the thickness-dependent SI transition of granular ultra-

thin ﬁlms, a metallic regime is indeed found before the transition to zero

resistance.

40,79,80

In contrast with the results mentioned above, this metal-

lic regime is found at relatively high temperatures. Das and Doniach,

Dalidovich and Phillips,

and Ng and Lee,

have presented theoretical

approaches to intervening metallic phases. Phillips and Dalidovich reviewed

the subject in a comprehensive manner.

7. Insulating Regimes

There has been considerable interest in the insulating regime. Palaanen

et al.,

were the ﬁrst to report a peak in R(B) above the critical ﬁeld of

a-In

ﬁlms. The Hall eﬀect also turned on near this ﬁeld.

They sug-

gested this was the signature of a transition or crossover between Bose and

Fermi insulators and that the order parameter amplitude was non-vanishing

in the insulating regime. Very recently there have been a number of papers

conﬁrming and extending this work.

42,86

–

An alternative to the Bose-to-

Fermi insulator crossover at this ﬁeld is that the insulating regime consists of

intermixed superconducting and normal phases. The understanding of this

phenomenon has attracted considerable attention as Steiner, Boebinger and

Kapitulnik have noted the similarity of data on some InO

ﬁlms to obser-

vations on cuprate superconductors, but with a much larger magnetic ﬁeld

scale for the latter.

They suggested that the insulating regime of cuprates

attained in high ﬁelds is a Bose insulator. The linear resistance can actually

fall to zero near criticality at suﬃciently low temperatures, as ﬁrst reported

by Sambandamurthy et al.,

for InO

ﬁlms and later for TiN by Baturina

et al.

The explanation of this “superinsulating” behavior in terms of a

macroscopic Coulomb blockade in large Josephson junction arrays

–

has

generated signiﬁcant controversy.

Recent work has shown that the appar-

ent switching to an insulating state may be a nonlinear thermal eﬀect.

95,96

Other support for the existence of Cooper pairs in the insulating regime

are the measurements of Markovic et al.,

of the anisotropic magnetore-

sistance of ﬁlms on the insulating side of the disorder-tuned SI transition,

August 24, 2010 17:25 World Scientiﬁc Review Volume - 9.75in x 6.5in ch12

Superconductor-Insulator Transitions 269

which support the idea that vortices are present. Gantmakher et al. con-

cluded from an analysis of magneto-transport in Cd-Sb alloys that there may

be localized pairs in the insulating state of this system.

Recently Crane

et al.

reported studies of the complex AC conductivity of InO

ﬁlms

through the magnetic ﬁeld tuned SI transition. The data revealed a nonzero

frequency superﬂuid stiﬀness well into the insulating regime. Stewart et al.,

(2007) presented results on quench-condensed a-Bi ﬁlms patterned with a

nano-honeycomb array of holes.

Insulating ﬁlms exhibited temperature-

dependent resistances and magnetoresistance oscillations dictated by the ﬂux

quantum h/2e, which were interpreted as of evidence of Cooper pairing in

the insulating regime. Nernst eﬀect measurements on the perpendicular ﬁeld

driven transition of Nb

1−x

ﬁlms also suggest the presence of supercon-

ducting coherence in the insulating regime.

–

8. Quantum and Classical Percolation

Shimshoni et al.,

and Sheshadri et al.,

100

suggested that the SI transi-

tion is percolative. This phenomenology would become applicable if ﬁlms

were either physically inhomogeneous or, if actually homogenous, were ren-

dered inhomogeneous by order parameter amplitude ﬂuctuations.

101

Resis-

tive transport then involves tunneling of vortices across weak-link-connected

superconducting domains. This scenario blurs the distinction between gran-

ular and homogenous systems. Percolation might also explain the fact that

the correlation length exponents found in ﬁnite size scaling analyses of some

SI transitions are close to the percolation exponent in 2D, which is ∼ 4/3.

Considering the temperature dependencies of the length scales controlling

percolation and the quantum critical point, Kapitulnik et al.

suggested

that scaling carried out using high temperature data would yield percola-

tion exponents, whereas low temperature data would be needed to ﬁnd quan-

tum critical exponents. Based on “super-universality” they also suggested

that the correlation length exponent, n = 7/3, and the critical resistance

should be h/2e

, or double the quantum resistance for pairs. Dubi et al.,

102

discussed a model based on quantum percolation and constructed a global

phase diagram.

Through a detailed study of scaling near the magnetic ﬁeld-tuned

superconductor-to-insulator transition in strongly disordered ﬁlms, Steiner,

Brezney and Kapitulnik

reported that results for a variety of materi-

als could be collapsed onto a single phase diagram consisting of two clear

branches, one with weak disorder and an intervening metallic phase, and

August 24, 2010 17:25 World Scientiﬁc Review Volume - 9.75in x 6.5in ch12

270 A. M. Goldman

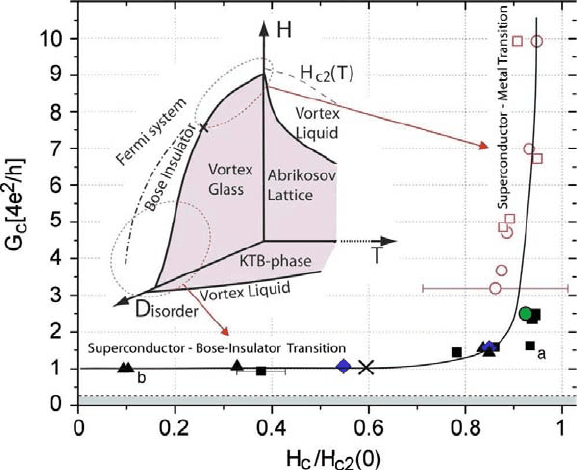
Fig. 5. Phase diagram including all samples, using reduced axes. The open circles

and squares are for MoGe ﬁlms. The full circle is for thin Ta ﬁlms.

The diamonds

are for InO

(Refs. 32 and 60); full triangles and squares are for InO

data; the

solid line is a guide to the eye. The X denotes a possible critical point between a

transition to a Bose insulator and a transition to a metal. The bottom-shaded area

denotes the region for which the conductance is smaller than h/e

. The inset shows

the low temperature part of the generic phase diagram as proposed in Ref. 35; the

crossover line between the Bose and Fermi insulators is terminated before reaching

zero disorder and does not reﬂect the possible emergence of a quantum metallic

state. (From Ref. 46.)

the other with strong disorder. Along the strongly disordered branch, they

reported that the resistance at the critical point approached the quantum

resistance for pairs, and the exponent product νz ∼ 2.3 ± 0.2, or 7/3 was

consistent with values associated with quantum percolation. Along the

weakly disordered branch there was an apparent intermediate metallic

regime and the critical resistance was below the quantum resistance for pairs.

Data from the strong disorder branch are all from In

ﬁlms, whereas the

low disorder branch consisted of Mo

and Ta ﬁlms. The proposed phase

diagram is shown in Fig. 5.

This work adds a diﬀerent twist to the study of the SI transition, sug-

gesting that while a true Bose-like SI transition can be achieved in the limit