Cooper L.N., Feldman D. (Eds.) BCS: 50 Years
Подождите немного. Документ загружается.

October 4, 2010 10:37 World Scientific Review Volume - 9.75in x 6.5in ch11
Cooper Pair Breaking 231
that implies a non-s wave pairing with an order parameter which changes sign
on translation through Q
z
= π/c. Here c is the lattice constant perpendicular
to the layers of U . An order parameter with a nodeline was indeed confirmed
experimentally.
32,36,48
A review of pair-breaking in superconductivity which summarizes the
situation of the theory in the late ’60s was given by Maki,
44
a pioneer in the
field. Many experimental results are also found in a review by Alloul et al.
3
In the following we want to discuss some of the most important concepts.
2. Time-reversal Symmetry Breaking
The Hamiltonian of an interacting electron system is time-reversal invariant,
i.e.
[H, T
R
]
−
= 0 . (1)
Here T
R
= −iσ
y
C is the time-reversal operator with C changing a function
into its complex conjugate and σ
y
denoting a Pauli matrix. This implies that
for each one-particle eigenstate Hψ
n
=
n
ψ
n
there exists a time reversed one
ψ
n
= T
R
ψ
n
with the same energy (Kramers’ theorem), i.e. Hψ
n
=
n
ψ
n
.
These two states can be paired to a ground state
|Φ
BCS
i =
Y
n
u
n
+ v
n
c
+
n
c
+
n
|0i, (2)
where c
+
n
creates an electron with wavefunction ψ
n
. When momentum and
spin are good quantum numbers it is n = (k, σ) and
n = (−k, −σ).
Let us assume that we add a perturbation to the system which violates
time-reversal symmetry. An example is
H
int
=
e
2m
X
i
(p
i
A + Ap
i
) − µ
B
X
i
σ
σ
σ
i
H (3)
where p
i
,σ
σ
σ
i
are momentum and spin of the i-th electron and A and H are
the vector potential and magnetic field, respectively. Another one is
H
int
= −(g − 1)J
ex
X
k,k
0
;αβ
c
+
k
0
α
σ
σ
σ
αβ
c
kβ
J (4)
where g is the Land´e factor and J is the total angular momentum of a
magnetic impurity. In those cases the time evolution of T
R
(t) does not
vanish any more and instead follows from
dT
R
dt
= i [H
int
, T
R
]
−
. (5)

October 4, 2010 10:37 World Scientific Review Volume - 9.75in x 6.5in ch11
232 P. Fulde
As shown by de Gennes
17
the linearized Ginzburg-Landau equation from
which the transition temperature T
c
is determined can be written in the
weak coupling limit in the form
1 = N(0)V
Z
dd
0
1 − f() − f(
0
)
+
0
g(
0
− ) . (6)
Here N(0)V is the BCS parameter f () is the Fermi function and most
importantly
g() =
Z
dt
2π
T
+
R
(0)T
R
(t)
e
−it
(7)
is the Fourier transformed correlation function of the time-reversal operator.
One notices that when H
int
= 0 or when H
int
is time-reversal invariant, we
obtain g( −
0
) = δ( −
0
) and (6) reduces to the well known BCS expres-
sion. Here we are interested in [H
int
, T
R
] 6= 0. In this case we must distin-
guish between two different long-time behaviors of the correlation function
hT
+
R
(0)T
R
(t)i. They are
(a) lim
t→∞
T
+
R
(0)T
R
(t)
= η , 0 < η < 1
(b) lim
t→∞
T
+
R
(0)T
R
(t)
= e
−2t/τ
R
. (8)
In the first case one speaks of nonergodic processes while the second one
implies ergodic behavior. The effect on T
c
and on Cooper pairing is quite
different in the two cases. Nonergodic behavior leads to pair weakening,
while ergodic behavior results in pair breaking.
When pair weakening takes place the transition temperature is
reduced to
k
B
T
c
= 1.13 ω
D
exp
−
1
ηN(0)V
, (9)
where ω
D
denotes a cut-off in the frequency of the bosons which provide
for the electron attractive interactions. The effect of the non-time-reversal
invariant interaction is just a reduction of the effective electron–electron
interaction. If, however ergodic behavior prevails we may set
g(z) =
1
2π
τ
R
1 + z
2
τ
2
R
/4
(10)
and after integrating (6) the equation for T
c
becomes
1 = N(0)V
X
n'0
1
n + 1/2 + 1/ (2πT
c
τ
R
)
. (11)
October 4, 2010 10:37 World Scientific Review Volume - 9.75in x 6.5in ch11
Cooper Pair Breaking 233
Note that here a cut off at ω
D
is still missing so that the sum is divergent.
After the cut off is introduced (11) becomes
ln(T
c
/T
c0
) + ψ
1
2
+
1
2πT
c
τ
R
− ψ(1/2) = 0 (12)
where ψ(x) is the digamma function.
1
The transition temperature T
c0
is
obtained when H
int
= 0. The last relation is the same which Abrikosov and
Gorkov obtained in their original work. One finds from (12) that T
c
/T
c0
drops continuously with increasing pair-breaking parameter 1/τ
R
and van-
ishes at a critical value of
1
τ
R
crit
=
πT
c0
2γ
; γ = 1.78 . (13)
3. Nonergodic versus Ergodic Behavior
As pointed out above, nonergodic behavior of time-reversal symmetry break-
ing leads to pair weakening instead of pair breaking. Two examples are given
for illustration. Consider a thin superconducting film of thickness d with a
rough surface but no scattering centers inside the film, when a magnetic field
is applied parallel to the film.
18
In that case
dT
R
dt
=
ie
m
(pA + Ap) T
R
= −i
dφ
dt
T
R
(14)
where φ(t) is the phase of the propagating electron. When the electron
moves straight from one surface of the film to the other, its phase does not
change (the vector potential has only a component perpendicular to the film
which is symmetric with respect to the film center). Therefore the only
contribution to dT
R
/dt comes from the parts of the path before it hits the
surface for the first time and after the last hit. Thus hT
+
R
(0)T
R
(t)i remains
finite even in the limit t → ∞. This results in pair weakening.
A second example concerns a staggered field imposed onto the conduction
electrons, i.e.
H
int
= −I
X
k,Q
h
Q
c
+
k↑
c
k+Q↑
−c
+
k↓
c
k+Q↓
. (15)
The Q’s are reciprocal lattice vectors of the magnetic lattice and are re-
stricted to the first Brillouin zone. It is
dT
R
dt
= 2iH
int
T
R
. (16)

October 4, 2010 10:37 World Scientific Review Volume - 9.75in x 6.5in ch11
234 P. Fulde
While [H
int
, T
R
] 6= 0 we find that the operator Y = T
R
R commutes with
H
int
, where R shifts the system by a vector connecting the two sublattices.
Thus [H
int
, Y ]
−
= 0. This is obvious: after application of T
R
the spins change
sign which increases their energy in the staggered field. By shifting the
electrons from one sublattice to the other the spin direction is again in line
with the staggered field. This implies that when ψ
kσ
(r) is an eigenfunction in
the staggered field so is Y ψ
kσ
(r) with the same eigenvalue. Therefore we may
pair ψ
kσ
(r) with e
iϕ
Y ψ
kσ
(r) where the phase ϕ is chosen by convenience.
Being able to pair electrons properly even when [H
int
, T
R
] 6= 0 shows that in
the presence of the interaction (15) Cooper pairs are possibly weakened but
not broken.
Next we turn towards ergodic behavior of perturbations. Thereby su-
perconductivity is discussed within the weak coupling limit. Systems with
pair-breaking interactions can be divided into two groups. Group 1 includes
all those cases for which a standard theory can be worked out for all temper-
atures. Group 2 comprises those situations for which a general pair-breaking
theory can be worked out only for the Ginzburg-Landau (GL) regime where
the order parameter is small. The GL equation is of the form
ln
T
T
c0
+ ψ
1
2
+ ρ
− ψ
1
2
D
|∆(r)|
2
E
+
1
2(2πT )
2
f
1
(ρ)
D
|∆(r)|
4
E
= 0
(17)
where f
1
(ρ) varies from case to case. The parameter ρ = (2πT τ
R
)
−1
is
a measure of the strength of pair breaking. The coefficient of h|∆(r)|
2
i is
the same as met before (see (12)) and is generic for all ergodic systems.
It determines T
c
. At lower temperatures the spatial variation of the order
parameter requires an individual treatment which is the reason for different
forms of f
1
(ρ).
We start with perturbations belonging to group 1. As pointed out before,
for that group a theory is available in closed form for all temperatures.
2
Dif-
ferent pair-breaking processes lead to equivalent forms of the single-particle
Green’s function where they enter in form of a pair-breaking parameter 1/τ
R
.
As a consequence, the thermodynamic properties expressed in terms of this
pair-breaking parameter are the same in all cases. For transport coefficients
this holds true too, but with one exception. We may obtain different expres-
sions when the relevant correlation function contains an s-wave spin triplet
vertex and when in addition the momentum transfer is less than (`ξ
0
)
−1/2
where ξ
0
is the coherence length.
45
This is the case, e.g. for the spin suscep-
tibility χ
s
(q, ω) when q is small. Otherwise different pair-breaking mecha-
nisms are completely equivalent.
45
The equivalence holds true in particular
October 4, 2010 10:37 World Scientific Review Volume - 9.75in x 6.5in ch11
Cooper Pair Breaking 235
for the density of states. In the BCS theory it is given by
N
S
(E) = N(0) Im
E/∆
p
1 − (E/∆)
2
(18)
where N(0) is the density of states per spin direction in the normal state. In
the presence of a pair-breaking parameter 1/τ
R
this expression is modified
to
N
S
(E) = N(0) Im
u
√
1 − u
2
(19)
where u(E) is a solution of the equation
E
∆
= u
1 −
1
τ
R
∆
1
√
1 − u
2
. (20)
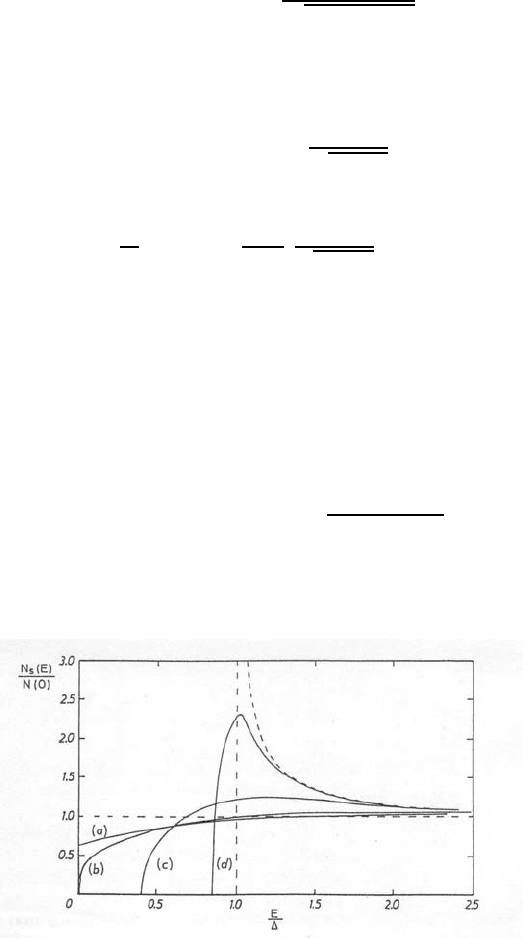
The latter has to be solved numerically and a plot is shown in Fig. 1.
For parameter values 0.91 < [(τ
R
)
crit
/τ
R
] < 1 where (τ
R
)
crit
denotes the
critical pair-breaking parameter at which T
c
vanishes, one finds no gap in
the excitation spectrum, i.e. the superconductor is gapless.
Gaplessness can again be rederived from the behavior of the time-reversal
operator T
R
.
17
Let us see under which circumstances the excitation energy
E
n
can be expanded for small order parameter ∆ in the form
E
n
= |
n
| +
D
|∆(r)|
2
E
X
m
|hn |T
R
|mi|
2
n
−
m
(21)
where |mi, |ni are single-electron states. When [H
int
, T
R
]
−
= 0 the matrix
elements hn|T
R
|mi 6= 0 only when |mi and |ni are time reversed. Then
Fig. 1. Tunneling density of states (per spin) as a function of energy E/∆ for
various values of τ
−1
R
. Curves (a)–(d) correspond to (τ
R
∆)
−1
= 1.33; 1.0; 0.5; 0.05,
respectively. (From Ref. 68)
October 4, 2010 10:37 World Scientific Review Volume - 9.75in x 6.5in ch11
236 P. Fulde
n
=
m
and the expression diverges. An expansion of that form is therefore
not allowed. If however [H
int
, T
R
]
−
6= 0 than hn|T
R
|mi 6= 0 for a range of
|
m
−
n
| ' τ
−1
R
. In this case we can write (21) in analogy to (6) as
E(p) = |(p)| +
D
|∆|
2
E
P
Z
d
0
(p) +
0
g(
0
− (p))
= |(p)| +
1
2
D
|∆(r)|
2
E
|(p)|
(p)
2
+ (τ
R
)
−2
. (22)
An expansion of the form (21) is therefore possible. Note that there is no
gap in E(p) in the limit of small ∆. From the last relation we obtain
N
S
(E) = N (0)
1 +
∆
2
2
E
2
− (1/τ
R
)
2
E
2
+ (1/τ
R
)
2
2
(23)
which agrees with the corresponding expression obtained from (19) and (20).
Perturbations belonging to group 1 include:
Paramagnetic impurities. As pointed out in the introduction, supercon-
ductors with paramagnetic impurities were the first in which gapless super-
conductivity was observed. The Hamiltonian is the one given by (4). The
spins of the magnetic impurities are treated classically. The scattering of con-
duction electron by the impurities is treated in Born approximation. This
excludes a possible Kondo effect which is discussed later. The pair-breaking
parameter is found to be
1
τ
R
= 2πn
I
N(0)(g − 1)
2
J
2
ex
J(J + 1) . (24)
The dependence of T
c
(n
I
) follows from (12) and a plot is found below in
Fig. 8.
Thin film in a parallel magnetic field. Here we have to distinguish
between local and nonlocal electrodynamics. In the first case the mean free
path ` must satisfy ` d where d is the film thickness. In addition the
conditions d λ, (`ξ
0
)
1/2
have to be fulfilled, where λ is the penetration
depth. The following pair-breaking parameter is obtained
39,41
1
τ
R
=
τ
tr
18
(v
F
edH)
2
. (25)
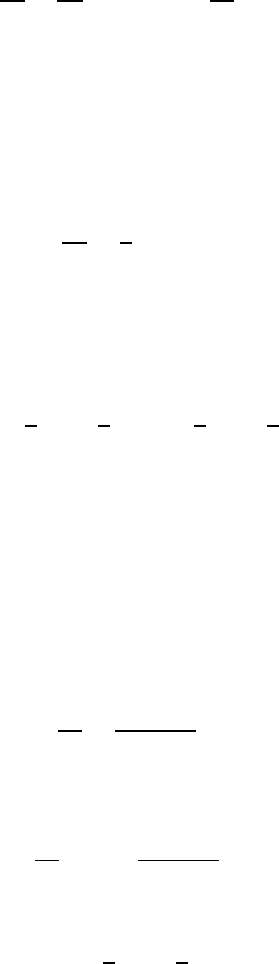
October 4, 2010 10:37 World Scientific Review Volume - 9.75in x 6.5in ch11
Cooper Pair Breaking 237
Note that τ
tr
is the transport mean free time while v
F
is the Fermi velocity.
In case of nonlocal electrodynamics d . ` the expression (25) is generalized
to
1
τ
R
=
τ
tr
18
(v
F
edH)
2
g
π`
d
, (26)
where g(x) = (3/2x
3
)[(1 + x
2
)arctan x − x].
75
The limit ` d reproduces
(25).
Supercurrent. In case of a uniform current time-reversal symmetry is
broken in the center of mass system because of scattering processes. When
` ξ
0
we find
1
τ
R
=
2
3
τ
tr
v
2
F
q
2
(27)
where q denotes the shift of the electron distribution in momentum space in
the presence of a current.
40
In the Ginzburg-Landau regime (see (17)) the function f
1
(ρ) applies to
all perturbations belonging to group 1
f
1
(ρ) = −
1
2
ψ
(2)
1
2
+ ρ
−
1
6
ψ
(3)
1
2
+ ρ
(28)
where ψ
(2)
(x) and ψ
(3)
(x) are higher derivatives of the digamma function.
Next we turn towards perturbations belonging to group 2 according to
the above classification scheme. The pair-breaking parameter τ
−1
R
applies
here to the Ginzburg-Landau regime (17) only. Two examples are discussed.
Type II superconductors. By restricting oneself to the effect of a mag-
netic field on the electron orbits, i.e. by neglecting the Zeeman term we
obtain in the dirty limit (`/ξ
0
1),
15,18,42
1
τ
R
=
τ
tr
v
2
F
eH
3
. (29)
When a magnetic field is applied, nucleation starts at the surface. In the
surface regime
60
1
τ
R
= 0.59
τ
tr
v
2
F
eH
3
. (30)
In the bulk as well as in the surface regime the function f
1
(ρ) is
f
1
(ρ) = −
1
2
ψ
(2)
1
2
+ ρ
. (31)

October 4, 2010 10:37 World Scientific Review Volume - 9.75in x 6.5in ch11
238 P. Fulde
Contact between a superconducting and a magnetic film. Boundary
conditions require that, at an interface between a superconductor and a
magnetic metal, the order parameter vanishes.
16
In the Ginzburg-Landau
regime close to T
c
the order parameter varies normal to the interface x = 0
like ∆(x) ∼ cos
πx
2d
s
where d
s
is the thickness of the superconducting film
which extends from 0 < x < d
s
. In the limit of ` d
s
and (`ξ
0
)
1/2
< d
s
the
pair-breaking parameter is
24,26
1
τ
R
=
τ
tr
v
2
F
6
π
2d
s
2
, (32)
while f
1
(ρ) is given by
f
1
(ρ) = −
1
2
ψ
(2)
1
2
+ ρ
+
1
18
ψ
(3)
1
2
+ ρ
. (33)
By comparison with (28) one notices that the term proportional to
ψ
(3)
1
2
+ ρ
depends sensitively on the spatial variation of ∆(r).
4. Zeeman Splitting of Quasiparticles
When a magnetic field is applied parallel to a very thin film, e.g. of Al with
20
˚
A thickness, the effect of the field on the spins dominates the one on the
orbits to the extent that the latter may be neglected. A similar argument
holds true for type II superconductor when the κ value, i.e. the ratio of pen-
etration depth to coherent length is very large. In both cases the transition
to the normal state is of first order provided that the spin-orbital mean free
path `
s0
= v
F
τ
s0
is not too small. Generally the density of states splits into
two parts
N
T
(E) =
N(0)
2
sgnE <e
u
+
q
u
2
±
− 1
+
u
−
q
u
2
±
−1
. (34)
The u
±
(E) are the solutions of the following coupled equations
E ∓ µ
B
H
∆
= u
±
+
i
3τ
s0
∆
u
±
− u
∓
q
u
2
∓
− 1
. (35)
The root has to be chosen so that (u
2
±
− 1)
1/2
→ u
±
sgn(Re u
±
) when
E → ±∞. In the special case that τ
s0
∆
0
1 (35) reduces to (20) with
the pair-breaking parameter given by
1
τ
R
=
3τ
s0
2v
F
(µ
B
H)
2
, (36)
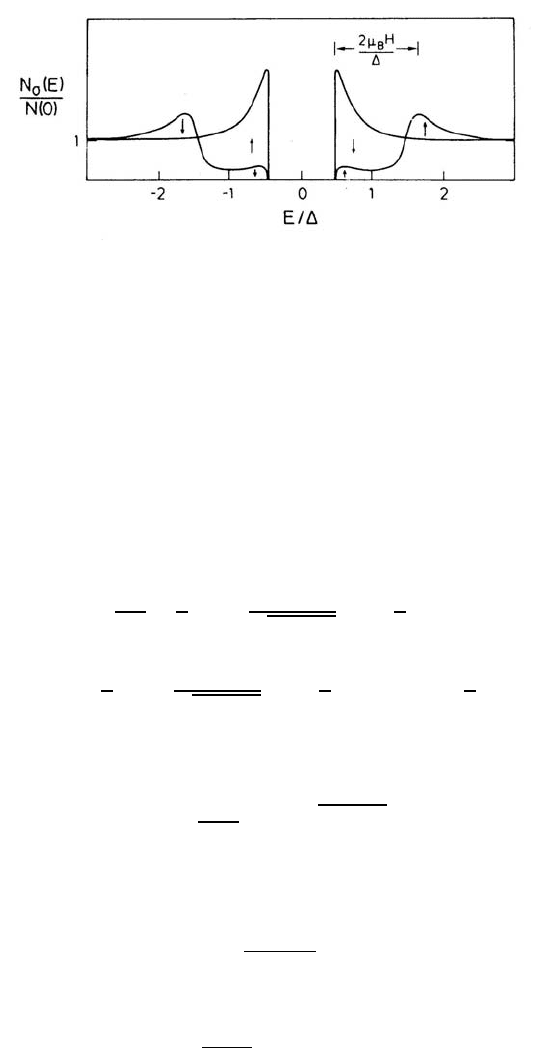
October 4, 2010 10:37 World Scientific Review Volume - 9.75in x 6.5in ch11
Cooper Pair Breaking 239
Fig. 2. Zeeman split quasiparticle density of states N
σ
(E). Due to the presence
of small spin-orbit scattering the two components are slightly mixed.
i.e. we are back to the standard pair-breaking theory. The Zeeman-split
density of states has been observed by Meservey and Tedrow in tunneling
experiments.
52,72
Since electrons do not change their spin during the tun-
neling process, the method can be applied as a tool to measure magnetic
properties.
73
An example of N
T
(E) based on (34) is shown in Fig. 2.
When the effect of the field on the orbits cannot be neglected, the pref-
actor α of the h|∆(r)|
2
i term in the Ginzburg-Landau equation is of the
form
α =
ln
T
T
c0
+
1
2
1 +
b
√
b
2
− h
2
ψ
1
2
+ ρ
−
+
1
2
1 −
b
√
b
2
− h
2
ψ
1
2
+ ρ
+
− ψ
1
2
. (37)
Here the abbreviations b = (3τ
s0
∆
0
)
−1
and h = µ
B
H/∆
0
have been intro-
duced. Furthermore
ρ
±
=
∆
0
2πT
n
a ±
p
b
2
−h
2
o
. (38)
The pair-breaking parameter a depends on the particular situation. For a
type II superconductor in the dirty limit it is given by
a =
τ
t
v
2
F
eH
3∆
0
+ b (39)
while for a thin film in a parallel field it is in the same limit
a =
τ
t
18∆
0
(v
F
edH)
2
+ b . (40)
The two forms of a should be compared with (29) and (25).

October 4, 2010 10:37 World Scientific Review Volume - 9.75in x 6.5in ch11
240 P. Fulde
Eu Sn Mo S Se
0.75 0.25 6 8−y y
25
20
15
10
5
0
S
y = 0.8
transition temperature T[K]
H[T]
1 2 3 4
Fig. 3. Field induced superconductivity based on the Jaccarino-Peter effect. (From
Ref. 53)
Equation (37) for a type II superconductor in a high field was first de-
rived by Werthamer, Helfand and Hohenberg.
76
It had been obtained before
for the case that the Zeeman term µ
B
σ
σ
σ ·H is caused by spin-polarized mag-
netic impurities, i.e. by a term −n
I
(g − 1)J
ex
σhJ
z
i.
25
Adding both terms,
i.e. working with a total Zeeman interaction of the form
H
Zeem
= −
X
i
σ
i
(µ
B
H − n
I
(g − 1)J
ex
hJ
z
i) (41)
can lead to a Jaccarino-Peter effect.
34
Here a compensation takes places
between the effect of an external field and that of polarized impurities which
couple via exchange to the conduction electrons. As a result, supercon-
ductivity may become magnetic field induced. This will be the case when
in the absence of a field the (unpolarized) magnetic ions have destroyed
superconductivity and when their effect is reduced by the aforementioned
compensation effect. Clearly that requires a delicate balance between dif-
ferent material properties. Nevertheless, field induced superconductivity
has been observed in Eu
0.5
Pb
0.5
Mo
6
S
8
53
(see Fig. 3) and apparently also in
λ-(BETS)
2
FeCl
4
.
31
The order of the phase transition from the superconducting to the
normal state in the presence of pair-breaking perturbations is obtained from
the sign of the function f
1
(ρ) in (17). When f
1
(ρ) = 0 a system changes
from a second- to a first-order phase transition. For perturbations belonging
to group 1 the phase transition is always of second order, while for those
