Cooper L.N., Feldman D. (Eds.) BCS: 50 Years

Подождите немного. Документ загружается.

September 2, 2010 15:31 World Scientiﬁc Review Volume - 9.75in x 6.5in ch13

Novel Phases of Vortices in Superconductors 281

May 3, 2010 17:58 World Scienti ﬁc Review Volume - 9.75in x 6.5in chapternewv9

4 F. Author and S. Author

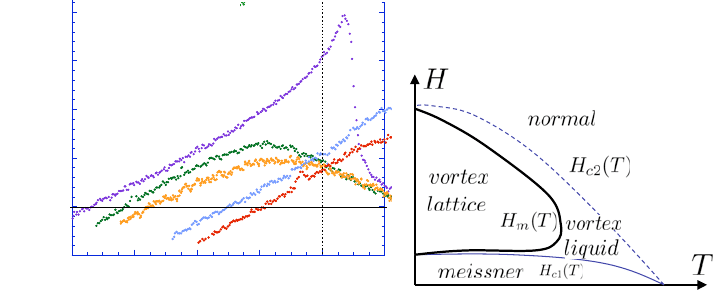
Fig. 1.2.

Fig. 1.3.

to the resistivity of the normal metal yields the Bardeen-Stephen estimate for the

friction η ≈ Φ

B/ρ

. Note that near a surface, the surface screening current

(which pushes the vortex inside) and the image vortex (which attracts it) conspire

to create, for H

< H < H

a surface barrier to vortex entry.

Thus to achieve a true dissipationless transp ort current one needs that vortices

Fig. 2. Left: Conventional v–f (E–j) characteristics at T = 0 (solid line). Creep

motion at small f is possible at T > 0 (dashed line) with nonzero linear resistivity

(linear slope). Right: Bean proﬁle, the slope



∼ j

is constant, upon increasing

the external ﬁeld (top) and upon decreasing the external ﬁeld (bottom) leading to

trapped ﬂux and to hysteretic magnetization loop upon cycling the ﬁeld.

of j on the curve of Fig. 2 implies a gradient in vortex density. Vortices

then tend to move towards lower density regions. However, since v vanishes

at j

the system gets blocked in one of the metastable states such that

everywhere



4π

or B = 0. Cycling of H under this constraint

yields a sequence of Bean metastable states with irreversible magnetization

irr

(H) ∼ B(H)−H. This gives rise to a hysteretic magnetization loop with

area proportional to j

times a geometric length in contrast to reversible

equilibrium magnetization in the absence of pinning (and of surface and

geometrical barriers).

2.2. Limits of the conventional picture

The above mean ﬁeld picture neglects the ﬂuctuations of the superconduct-

ing order parameter ψ(x) and, in the mixed phase, also the ﬂuctuations

in the positions of the vortex lines. These ﬂuctuations are thermal and

quantum ﬂuctuations or deformations of the vortex lines induced by pinning

disorder. Amazingly, and simplifying a little, a detailed understanding of

those has not proved crucial to account for the physics of conventional low

superconductors until the middle of the ’80s.

This situation became untenable with the advent of the high T

super-

conductors which led to a host of new phenomena and concepts in vortex

physics and raised many questions. Some have been answered, others remain

open. Many of these questions are related to the correct treatment of these

September 2, 2010 15:31 World Scientiﬁc Review Volume - 9.75in x 6.5in ch13

282 P. Le Doussal

ﬂuctuations. Interestingly, this has pushed for a fruitful re-examination of

some lower T

superconductors, such as NbSe

Some of these questions were anticipated. Ten years after Abrikosov,

Eilenberger

showed that thermal ﬂuctuations of |ψ|, can become non-

negligible, i.e. δ|ψ|

/|ψ|

= O(1), but only in a hard to observe window

(with realistic parameters at the time) near (H

− B)/H

≈ 10

−4

. Inter-

estingly, his treatment, i.e. within the lowest Landau level (LLL) led already

to the idea of melting while retaining identity of vortices.

Similarly, a treatment of pinning neglecting deformations of the vortex

lines is not consistent. A strictly straight vortex line would simply “average”

over point impurities, leading to a vanishingly small f

∼ L

−1/2

as its length

L increases. The very nature of pinning requires vortex deformations that

lower the energy. The modern theory of pinning started with the pioneering

works of Larkin and Ovchinnikov.

13,14

Below the threshold f < f

, the combined eﬀect of thermal ﬂuctuations

and pinning was known to lead to “ﬂux creep” by relaxation over the bar-

riers. It was described in terms of a particle (representing a blob of pinned

lattice) moving by thermal activation over a 1D energy landscape with ﬁxed

barriers U

, a model called Thermally Assisted Flux Flow (TAFF)

which

predicts a linear response v ∼ f at small force, although with a reduced

resistivity ρ = ρ

−U

. The rounding of the v − f curve near f

implies

thermal relaxation of the Bean proﬁle to a uniform one. However for low

materials U

/T is large and this would occur on gigantic time scales. In

practice only the region f . f

relaxes. There the TAFF model predicts

v = v

exp



(j − j

)



which leads to the very slow logarithmic relaxation

of what is called the persistent current j(t) ≈ j



1 −

ln t



which was ob-

served in low T

materials.

16,17

For these relaxation eﬀects, being extremely

small in low T

materials, there was no need to develop a deeper understand-

ing of the creep process, e.g. to take into account the deformations of the

vortex lattice during the motion.

2.3. The new picture: the vortex matter

2.3.1. Material characteristics and early experimental facts

The ﬁrst characteristic of the new superconductors, besides high T

, e.g. 92 K

for YBa

7−δ

(YBCO) and T

= 135 K for HgBa

, is that

they are layered materials, mainly ab superconducting planes separated along

c-axis by insulating layers. They are insulators which become supercon-

September 2, 2010 15:31 World Scientiﬁc Review Volume - 9.75in x 6.5in ch13

Novel Phases of Vortices in Superconductors 283

ductors under doping. Despite the unconventional microscopic mechanism

and the d wave character of the order parameter,

it is usually accepted

that, apart from a few speciﬁc points (some mentioned below), they can be

described by the anisotropic version of the Ginzburg–Landau model, with

mainly c-axis anisotropy. One distinguishes the penetration and coherence

lengths, as well as the eﬀective masses, along ab-plane, noted here λ

≡ λ,

≡ ξ, m ≡ m

and along c-axis, ξ

, λ

and m

. The anisotropy parameter

 =

 1, e.g. 

YBCO

= 0.16. One still denotes κ = λ/ξ

and uses (1). The critical ﬁelds are H

2πξ

= H

and H

4πλ

ln κ.

High T

superconductors are strongly type II i.e. κ ≈ 10

, hence

∼ κ

∼ 10

with H

= O(100G) and H

= O(100T ). The

mixed phase is thus huge and crucial for applications. The London ap-

proximation, which neglects the spatial variations of the modulus of the

order parameter, works in most of the phase diagram. The vortex lattice

spacing a

≈ 480A/

B(Tesla) varies over two orders of magnitude from

∼ λ ∼ 0.2µm for B ∼ H

to a

∼ ξ ∼ 20

A near H

(outside the critical

regions).

In the most anisotropic compounds, such as Bi

CaCu

8+δ

(BSCCO)

with 

BSCCO

= 10

−2

, the interlayer transport is essentially via Josephson

eﬀect and one must replace the anisotropic GL model by its discretized

version along the c-axis, the Lawrence–Doniach model. The ﬂux lines then

become rather a superposition of so-called pancake vortices which live and

can move in each ab plane. A new transition is then predicted to occur:

decoupling of the layers with loss of the critical current along z.

19–21

The importance of thermal ﬂuctuations can be appreciated from the ratio

of temperature to condensation energy in a coherence volume, the Ginzburg

number Gi = (T

√

2

(0)ξ(0))

a material parameter which also gives

the temperature window 1−t < Gi, t = T /T

over which critical ﬂuctuations

cannot be ignored within the GL theory. In conventional superconductors

Gi ∼ 10

−8

and pinning is strong j

∼ 10

−2

− 10

−1

while in high T

superconductors Gi ∼ 10

−2

and pinning is weaker j

∼ 10

−2

− 10

−3

A ﬁrst striking feature of experiments on high T

materials, is that one

does not observe the jump in the speciﬁc heat predicted by mean ﬁeld theory

at the mean ﬁeld H

(T ). Instead there is only a broad maximum around

that location, which broadens as the ﬁeld increases, as in Fig. 3. The max-

imum itself shows active degrees of freedom and suggests that there are

vortices. Below we denote H

(T ) (and respectively T

(H)) the location of

Here and below ξ(0), etc. means T = 0 value.

September 2, 2010 15:31 World Scientiﬁc Review Volume - 9.75in x 6.5in ch13

284 P. Le Doussal

La fusion du réseau de vortex :

une nouvelle transition de phase du 1

ordre

YBa

0.99

1.01

1.02

1.03

1.04

1.05

0.92 0.94 0.96 0.98 1 1.02

t = T / T

0.99

1.01

84 86 88

B = 4T

B = 3T

T (K)

Mesures p ar

R. Brusetti;

voir C.J. van der

Beek et al. PRB 72,

214405 (2005)

0.99

1.01

84 86 88

B = 4T

B = 3T

T (K)

A. Schilling et al., n ature 382, 791 (1996);

M. Roulin, A. Junod, et E. Walker, Science 273, 1210 (1996)

75 80 85 90 95

B ( T )

T ( K )

Dépiégeage

(volume)

Fusion

(1er ordre)

Q = 7.9

max. C

Q = 3.2

liquide

de vortex

= 0

solide de vortex

> 0

May 3, 2010 17:58 World Scientiﬁc Review Volume - 9.75in x 6.5in chapternewv9

New phases of vorticesin superconductors 5

Fig. 1.4.

Fig. 1.5.

be pinned. Pinning is provided by impurities in the material. Since they weaken

superconductivity locally, they are energetically favorable positions for the vortex

core to sit. The conventional description of pinning replaces (1.2) by:

ηv =(f − f

)θ(f − f

) (1.3)

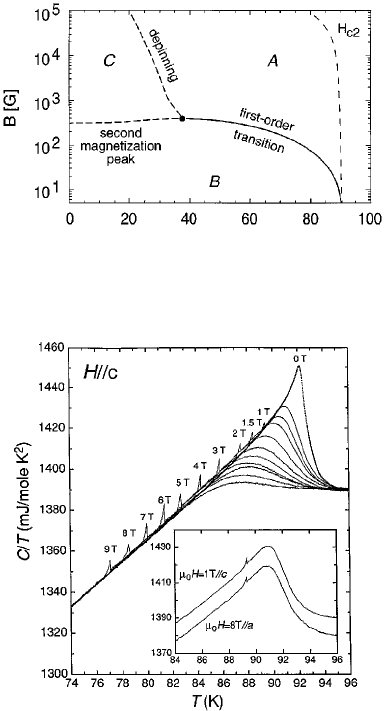
Fig. 3. Left: Speciﬁc heat of YBCO with the phonon background substracted,

from.

Right: Sketch of the expected phase diagram in the absence of pinning

disorder.

the mean ﬁeld transition even though it does not correspond to a genuine

phase transition.

Early experiments gave many hints that the vortex lattice could be melted

in a large fraction of the phase diagram. Transport measurements

showed

a suppression of the critical current and a long resistive tail much below

the superconductor-to-normal transition in BSCCO in ﬁelds above ∼ 0.5T .

These results suggest that vortices ﬂow freely, without a shear modulus, in

response to an arbitrary small driving force over the larger part of the B(T )

phase diagram, down to temperatures as low as 35 K. Torque measurement

on the same material found that damping of mechanical oscillations change

drastically at this temperature.

Being dynamical in nature, these experi-

ments were mainly an evidence for a transition from a pinned regime to an

unpinned one, not a direct proof of melting. The main experimental fact

was the existence

of an irreversibility line H

irr

(T ) far below H

separat-

ing these two regimes. At the same time, magnetic decoration on YBCO,

performed at much lower ﬁelds near H

, showed that the vortex lattice,

well-formed at higher ﬁelds, becomes disordered at low vortex density.

26,27

Separating dynamics from thermodynamics was thus the main challenge.

The order of the transition (continuous versus ﬁrst-order) was also not clear.

Giant ﬂux creep relaxation was observed

and another unusual feature, the

ﬁshtail or second magnetization peak was also observed at low temperature

(see below).

September 2, 2010 15:31 World Scientiﬁc Review Volume - 9.75in x 6.5in ch13

Novel Phases of Vortices in Superconductors 285

2.3.2. New theories

For theorists the challenge was to develop the GL theory beyond mean ﬁeld.

There are two main ways to describe the ﬂuctuations in the mixed phase,

which are dual to each other. One can either use a description in terms of the

complex order parameter ψ(r), with its phase and modulus. This approach

is more convenient near H

(T ), where the LLL approximation can be used.

Alternatively, one can describe ﬂuctuations in terms of the displacements

of individual vortex lines u

(z), more convenient when the latter are well-

separated and the London approximation can be used (B . 0.2H

). One

must then describe the statistical mechanics of interacting line objects.

In the absence of quenched disorder, this second approach naturally led

to two phases: (i) a vortex solid where the energy of deformations of the

vortex lattice are described by standard elastic theory, adapted to a solid

set of lines. The simplest description requires the in-plane bulk and shear

modulus c

, c

and a tilt modulus c

for deformations of the vortex lines

away from the direction of the external ﬁeld. These are both ﬁeld, B,

and wave-vector, q, dependent, i.e. the elasticity is non-local and the VL

is softer at its smallest scales ∼ a. They were calculated quite precisely

29–31

(ii) a vortex liquid phase, described as a collection of ﬂuctuating entangled

lines

: an analogy, most useful in the small ﬁeld region B  H

, maps

vortex lines in 3D onto imaginary time world lines of 2D bosons and allows

one to estimate the entropy of the liquid. The two phases are separated

by a melting line H

(T ). Its position was estimated from the usual Lin-

demann criterion for the melting of a 3D solid, from the thermal average

i = c

, where the Lindemann constant c

= 0.1 − 0.4 in standard

solids. The simplest estimates (see Sec. 3.4) yields T

∼ a

√

, and

using c

∼ 

and c

∼ 



yields B

∼ Φ



. Near T

, and

for B

 H

one must take into account the temperature dependence of

λ, leading to B

≈ 5.6(c

/Gi)H

(0)(1−T/T

)

. More accurate predictions

valid for larger B

were made taking into account the full non-local elastic-

ity.

A sketch of the melting line is shown in Fig. 3. The melting line is

reentrant near H

(T ) since the density of vortices and the shear modulus

vanish there.

Although useful, the Lindemann criterion does not provide a true theory

of melting. While the superﬁcial analogy with 3D solids suggests ﬁrst-order

melting, it is not so obvious for the superconductor since a detailed theory

should start from the GL model and describe both the formation of the

Abrikosov lattice and the ﬂuctuations of ψ(r), and, indeed, in mean-ﬁeld,

the transition is second order! Early attempts

to include ﬂuctuations in the

September 2, 2010 15:31 World Scientiﬁc Review Volume - 9.75in x 6.5in ch13

286 P. Le Doussal

LLL approach suggested that these induce a ﬁrst order transition (FOT),

however the approach is diﬃcult.

Some success was obtained to treat

ﬂuctuations due to condensation energy and to compute smooth variations

of the thermodynamics functions.

More recently, as experimental evidence

for a FOT became overwhelming, precise calculations of the free energy

of both the solid and the liquid, were performed within GL. They allow

one to account for the FOT and to calculate the value of the Lindemann

number.

36–40

Numerical simulations

have also seen a ﬁrst order transition.

The melting transition is developed in Sec. 3.

An order parameter for the solid is the translational order correlation,

expressed in terms of vortex displacements as the translational average h··i

over the sample:

(x) = he

iK·u(x)

−iK·u(0)

i (4)

Here it is equivalent to the thermal average (denoted h··i). It is also

equal to the Fourier transform of the vortex density correlation S(k) =

hρ

(−k)ρ

(k)i for k

⊥

near K, a 2D reciprocal lattice vector of the (e.g. tri-

angular) vortex lattice. S(k) is measured from neutron diﬀraction experi-

ments, up to a form factor due to the distribution of B(x) around a vortex.

In the perfect solid C

(x) decays to a constant, e

−

the Debye–Waller

factor, leading to δ-function Bragg peaks in S(k) at the reciprocal lattice,

equivalently he

−iK·u

i 6= 0. In the ﬂux liquid, S(k) exhibits instead broad

isotropic 2D rings around k ∼ π/a

: there is no in-plane translational or-

der, and vortex lines u

(z) wander diﬀusively in the z direction.

It can be

obtained from the elastic solid by letting dislocation and disclination loops

proliferate,

which drive the shear modulus to zero. Within the GL descrip-

tion, the ﬂux liquid is described as ﬂuctuations around ψ(x) = 0, i.e. it is

continuously related to the normal phase, with no change in symmetry.

The outstanding question was how this picture is modiﬁed in the presence

of pinning disorder. Many early experiments showed rather a continuous

transition occuring at the irreversibility line.

Two main approaches were

put forward. Both agreed on one property: the vortex lattice is changed into

a glass. A glass induced by quenched disorder has a non-trivial disordered

ground state, and the energy cost of excitations on scale L is a positive ran-

dom variable which grows typically as L

with θ > 0. The ﬁrst approach,

known as vortex glass

44,45

was inspired from spin glasses, and postulated

the existence of an oﬀ-diagonal order parameter

|hψ(x)i|

6= 0, i.e. in each

sample hψ(x)i is non-zero but non-uniform and random. While mostly phe-

nomenological, it could be argued assuming that the quenched disorder has

destroyed the vortex lattice,

leaving a description only in terms of a simpler

September 2, 2010 15:31 World Scientiﬁc Review Volume - 9.75in x 6.5in ch13

Novel Phases of Vortices in Superconductors 287

discrete XY model with a quenched random gauge ﬁeld A(x). Numerics

found that this gauge glass model could indeed exhibit a glass phase in d = 3,

i.e. with θ > 0.

The second approach retains the elastic lattice structure at small scale

and describes the coupling of disorder to the vortex displacement ﬁeld u(r, z).

The problem becomes a particular case of the more general problem of an

elastic manifold in a random potential. Theoretical progress in that more

general problem, described in great detail in Sec. 4, lead to the picture of

collective pinning and also to a glass phase beyond the so-called Larkin length

. The precise nature of this phase was however unclear for a while. Larkin

had found

that the deformations δu(x) = u(x) −u(0) induced by disorder

grow with scale x, i.e. the standard Abrikosov lattice was unstable even to

the weakest disorder. A possible scenario was thus that the translational

order correlation would decay fast beyond a second length scale, R

, such

that u ∼ a, and that beyond a length R

∼ R

dislocations in the vortex

lattice could become favorable, leading to a topologically disordered state,

as argued in the vortex glass picture.

It was then argued

that the Abrikosov vortex lattice is replaced by a

distinct new phase of vortex matter, the Bragg glass (BrG), which retains

topological order but not translational order. There are no unpaired dis-

locations in the ground state, so in that sense the Abrikosov lattice is not

destroyed. On the other hand, the translational order correlation C

(r)

decays beyond R

, but slowly, only as a power law, very much as in 2D

quasi-solids. As a consequence, there should be observable Bragg peaks.

At the same time it is a glass. The asymptotic energy exponent is found as

θ = d−2.

47,50

The BrG theory, detailed below, is based on both a variational

theory and renormalization group calculations, as well as energy arguments

which indicate that indeed dislocation lines cost more energy than they allow

one to gain.

Most importantly, the hallmark of a true glass being also the existence of

diverging barriers between low-lying states, it was argued that to describe

creep, the TAFF law should be replaced by:

v ∼ ρ

−U

(j)/T

(5)

with an eﬀective barrier U

(j) ∼ (j

/j)

−µ

at small j. Within the vortex

glass picture, this was expected based on the conjecture of a glass phase.

Within the elastic approach it could be argued on a more solid basis, within

the collective creep theory

48–52

as we will describe in Sec. 4, but only if one

assumed the absence of dislocations. The Bragg glass then, with its topolog-

September 2, 2010 15:31 World Scientiﬁc Review Volume - 9.75in x 6.5in ch13

288 P. Le Doussal

ical order, guarantees the law (5) with µ = 1/2 asymptotically provided the

lowest lying excitations are purely elastic. This implies ultra-slow relaxation

at very small current j  j

and zero linear resistivity, i.e a true supercon-

ductor. Thus having a glass is essential for true superconductivity, a very

new concept as compared to the conventional TAFF picture.

Conversely,

(5) also implies, in high T

materials where pinning is weaker, that for larger

j near j

there is a lot of relaxation, accounting for the observations of giant

ﬂux creep and relaxation of the Bean proﬁle and of the persistent current

with nonlinear logarithmic decay in time j ∼ (T ln t)

−1/µ

2.3.3. Experiments meet theory: towards a phase diagram

Since the vortex glass ideas suggested a continuous transition, a phenomeno-

logical picture of what a continuous glass transition should look like was de-

veloped, based only on the hypothesis of a single diverging length scale at the

transition and standard critical scaling.

43–45

It was used then to interpret

numerous experiments, but being quite generic, it did not carry information

on the detailed nature of the glass phase.

Quite diﬀerent results were soon obtained, however. In untwinned YBCO

single crystals sharp jumps in resistivity were observed

55–58

as shown in

Fig. 4, delimiting a ﬁrst order transition line between a pinned supercon-

ducting phase and the liquid. In BSCCO, where anisotropy is larger and

pinning weaker, the irreversibility line, i.e. the opening of the magnetiza-

tion loop, lies signiﬁcantly below the melting line, hence thermodynamic

evidence of ﬁrst-order equilibrium melting was easier to obtain. The local

ﬁeld B, i.e. the vortex density, measured using microscopic Hall sensors,

showed a discontinuous step at the transition,

shown in Fig. 5, as in a

standard solid. The density of the vortex liquid being larger than the solid,

as in ice, was interpreted from the entropy gain of letting neighboring vortex

lines entangle in the liquid.

The phase diagram measured for BSCCO is

shown in Fig. 6, where A is a reversible ﬂux liquid, B an ordered vortex

solid and C an amorphous or disordered solid. Neutron diﬀraction

showed

Bragg peaks in the B phase, but no peaks in the C and A phases, while muon

spin rotation experiments

showed loss of the triangular lattice lineshape as

one goes from B to C. Thermodynamic evidence for a ﬁrst order transition

came also in YBCO

as a spike in the speciﬁc heat, superposed on the broad

maximum, as in Fig. 7. The phase diagram for YBCCO and BSCCO started

to look alike, with a FOT at low ﬁeld and a continuous one at high ﬁeld,

separated by what appeared then as a tri-critical point. Since higher ﬁelds

(in that range) correspond to stronger disorder as the density of vortices

September 2, 2010 15:31 World Scientiﬁc Review Volume - 9.75in x 6.5in ch13

Novel Phases of Vortices in Superconductors 289

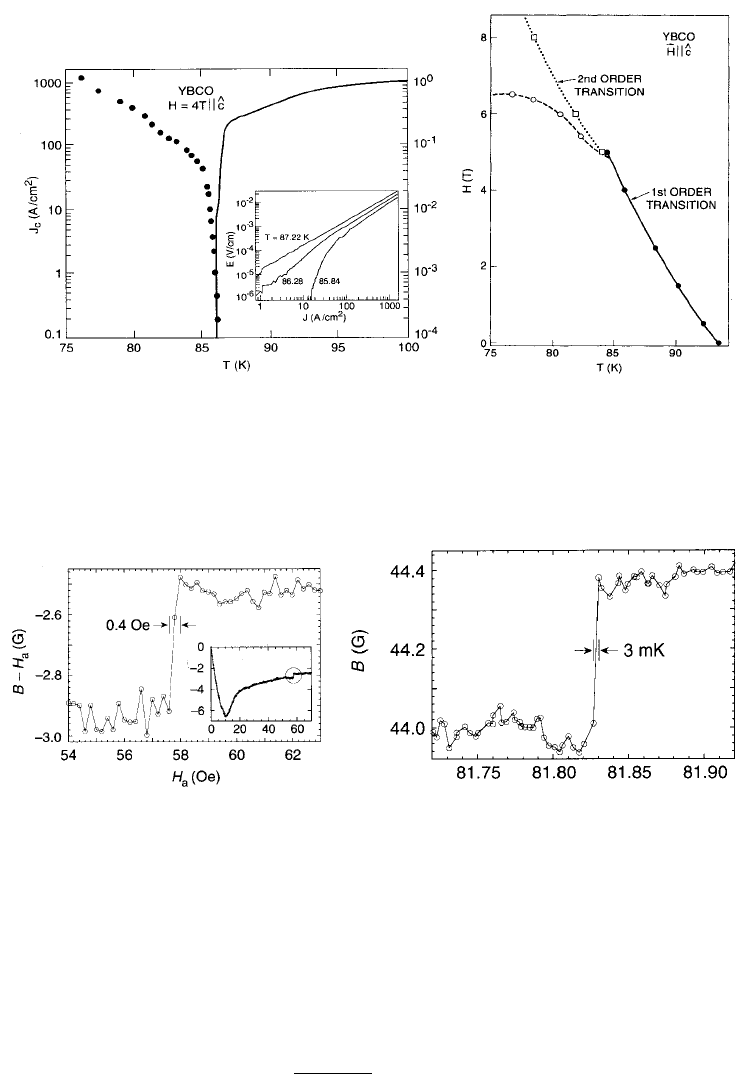
Fig. 4. Left: Linear response resistance (right axis) and critical current as a func-

tion of temperature for YBCO at H = 4T near melting. Right: Phase diagram

— (solid circle) jumps in resistivity, (squares) continuous transition, (open circles)

minimum in v (similar to the maximum of j

in magnetization). From Ref. 58.

Fig. 5. Sharp jump in local B in BSCCO as H is varied (left) or T (right), evidence

of a thermodynamic FOT, from Ref. 59.

is larger, this was in agreement with the idea of two distinct glass phases:

(i) a weak disorder phase, the Bragg glass, close to a perfect solid, which

would naturally melt through a ﬁrst order transition (ii) a strong disorder

phase which would be amorphous. As seen in Fig. 9, it was also found that

the apparent tricritical point is lowered in ﬁeld upon increasing the weak

point disorder by electron irradiation or by changing the doping. An ex-

tended Lindemann criterion,

hδu(a)

i ∼ c

, i.e. R

∼ a, which estimates

September 2, 2010 15:31 World Scientiﬁc Review Volume - 9.75in x 6.5in ch13

290 P. Le Doussal

Vortex-matter phase transitions in Bi

CaCu

: Effects of weak disorder

B. Khaykovich

Department of Condensed Matter Physics, The Weizmann Institute of Science, 76100 Rehovot, Israel

and CNRS, URA 1380, Laboratoire des Solides Irradie

s, E

cole Polytechnique, 91128 Palaiseau, France

M. Konczykowski

CNRS, URA 1380, Laboratoire des Solides Irradie

s, E

cole Polytechnique, 91128 Palaiseau, France

E. Zeldov, R. A. Doyle, and D. Majer

Department of Condensed Matter Physics, The Weizmann Institute of Science, 76100 Rehovot, Israel

P. H. Kes and T. W. Li

Kamerlingh Onnes Laboratorium, Rijksuniversiteit Leiden, P.O. Box 9506, 2300 RA Leiden, The Netherlands

!Received 11 April 1997"

The vortex matter phase diagram in Bi

CaCu

crystals is investigated by introducing very low doses

of point and correlated disorder. We conclude that at least three distinct phases are present. The ordered

low-ﬁeld quasilattice phase has a ﬁnite shear modulus which vanishes at the ﬁrst-order melting or sublimation

transition at elevated temperatures. At lower temperatures the quasilattice transforms into a disordered solid as

ﬁeld is increased above the second magnetization peak. This disorder-driven transition shifts to lower ﬁelds

with increased point disorder. The ﬁrst-order transition displays corresponding downward curvature in the

vicinity of the critical point. #S0163-1829!97"51526-8$

The behavior of vortices in type-II superconductors is de-

termined by complex repulsive interactions between each

other and by attractive interactions with the material defects.

Thus the vortex matter structure is a complicated function of

temperature, magnetic ﬁeld, and material disorder.

This re-

sults in a rich phase diagram which is divided by numerous

phase transitions and crossovers, the exact natures of which

are still not resolved. Over the last few years it has become

apparent that in high-temperature superconductors thermal

ﬂuctuations cause melting of the vortex lattice, thus forming

two distinct phases, the vortex solid and the vortex liquid.

1,2

However, in highly anisotropic superconductors like

CaCu

!BSCCO" an unexpected additional phase

boundary, the so called second magnetization peak, appears

to exist within the region that is assumed to be the vortex

solid.

3–6

The second peak transition forms an almost hori-

zontal line in the low ﬁeld and low temperature region of the

B-T phase diagram !Fig. 1". Another fascinating feature of

the vortex matter is the experimentally observed ﬁrst-order

phase transition !FOT".

7–12

The position of the FOT line on

the phase diagram of BSCCO is shown in Fig. 1. This tran-

sition is expected, and indeed observed to occur only in very

clean systems, whereas continuous transition or crossover is

anticipated in the presence of strong disorder.

The exact

nature of the observed FOT is still unclear. The three pre-

vailing theoretical descriptions of the FOT can be classiﬁed

as melting, evaporation, or sublimation.

The more com-

monly accepted scenario is melting of an ordered solid vor-

tex lattice into a liquid of vortex lines.

1,2

In the evaporation

!decoupling" transition the vortex-line liquid dissociates into

a gas of uncorrelated vortex pancakes in the individual CuO

planes.

Recently a sublimation transition !simultaneous

melting and decoupling" was proposed in which the solid

vortex lattice undergoes a direct transition into the pancake

gas.

Figure 1 also shows a third experimentally observed

boundary line, the depinning line, where the bulk pinning of

the vortices drops below a detectable level.

The emerging experimental picture of Fig. 1 is that the

vortex matter seems to display at least three distinct phases

with three phase boundary lines, rather than two main phases

!solid and liquid" with only one transition line between them.

In this paper we elucidate the structure of the different vortex

phases !indicated as A, B, and C in Fig. 1" and the nature of

the transitions between them. Our approach is based on con-

trolled introduction of very low doses of point and correlated

disorder as a weakly perturbative tool to investigate the un-

derlying physical phenomena. Until now most experimental

and theoretical efforts have focused on the rather extreme

cases of clean

1,2,5–14

and highly disordered systems,

1,16

re-

spectively. In contrast, the general knowledge of the effects

of weak disorder is very limited.

3,17

We ﬁnd that by exposing

FIG. 1. Schematic vortex matter phase diagram in BSCCO !on a loga-

rithmic scale". The major part of the diagram is occupied by phase A which

is a vortex liquid !or a gas of vortex pancakes". Phase B is a rather ordered

solid quasilattice, whereas phase C is a highly disordered vortex solid. At

elevated temperatures the quasilattice is destroyed by thermally-induced

melting !or sublimation" at the FOT. At low temperatures a disorder-driven

solid-solid transition occurs at the anomalous second magnetization peak.

The disordered solid, C, melts continuously at the depinning line.

RAPID COMMUNICATIONS

PHYSICAL REVIEW B 1 JULY 1997-IIVOLUME 56, NUMBER 2

Fig. 6. Phase diagram in BSCCO: An unpinned liquid, B vortex solid (Bragg

glass), C pinned amorphous phase, from Ref. 61.

VOLUME 78, NUMBER 25 P H Y S I C A L R E V I E W L E T T E R S 23 JUNE 1997

FIG. 1. Total speciﬁc heat of an untwinned YBa

72d

single crystal for H k c. The numbers on top of the peaklike

speciﬁc-heat features indicate the strength of the externally

applied magnetic ﬁeld. The inset shows representative data

for m

H ! 1 T k c and m

H ! 8 T k a (shifted vertically by

210 mJ!mole K

for clarity).

conﬁgurations. As a consequence of the apparent scaling

of these features, the melting ﬁelds H

"T # in the H-T

phase diagram differ by a factor $8 for the two conﬁgu-

rations. An empirical power-law ﬁt to all the data with

! H

"1 2 T !T

for H k c and H

! gH

"1 2

T !T

for H k a gives m

! "87.3 6 3.1# T, T

FIG. 2. Speciﬁc-heat differences C"H#!T 2 C"0#!T vs T ,

for H k c (a) and H k a ( b). In each ﬁgure, the curves have

been shifted arbitrarily for clarity.

"91.87 6 0.04# K, n ! "1.24 6 0.02#, and an anisotropy

ratio g ! "m

1!2

! " 7.76 6 0.15#, with the effec-

tive charge-carrier masses m

and m

for current trans-

port k c and ! c, respectively [14,17,18]. This latter

value is consistent with the results of other experiments

probing the angular dependence of vortex-lattice melting

in YBa

72d

(g $ 7.4 8.7 [12,14,19]).

The latent heats L ! T DS can be obtained by inte-

grating the area under the peaks in the C!T vs T curves

[16]. At a ﬁxed T , the entropy discontinuity DS per

unit volume is approximately the same for both geome-

tries [see Fig. 4(a), inset], indicating that DS!H

(which

is proportional to DS per vortex) scales with a factor

of the order of g. It has become a standard procedure

to use the unit “per vortex per superconducting layer”

(with the spacing of the layers usually taken as the dis-

tance c between the CuO

double layers) for latent heats

measured for H k c, although in the quasi-3D system

YBa

72d

one independent vortex segment contribut-

ing additional degrees of freedom may extend over several

FIG. 3. Comparison between the speciﬁc-heat differences

C"H #!T 2 C"0#!T measured in various external magnetic

ﬁelds, for H k c (upper curves, shifted by 11.5 mJ!mole K

)

and H k a (lower curves). The magnetic-ﬁeld values for each

pair of curves differ by a factor 8.

4834

Fig. 7. Speciﬁc heat of untwinned YBCO, from Ref. 64.

when the BrG must become unstable to thermal and disorder-induced dislo-

cations,

66,67

was consistent with these observations. It furthermore indicated

a disorder-induced transition line H

(T ) away from the BrG, horizontal at

low T , as a simple continuation of the melting line. Strong downward renor-

malization of disorder was also predicted from ﬂux line thermal wandering,

producing in some cases a pronounced maximum in H

(T ) as it merges into

the melting line.

There was indeed a feature in the magnetic hysteresis loop at low T ,

ubiquitous in all high T

superconductors, a second peak in M(H) also called

ﬁshtail (see Fig. 8). Being in the irreversible non-equilibrium region, it could

be broad or sharp depending on ramping rate or history, and was the signa-