Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models

Подождите немного. Документ загружается.

40 CHAPTER R A Review of Basic Concepts and Skills R–40

College Algebra Graphs & Models—

EXAMPLE 1

䊳

Factoring Polynomials

Factor each polynomial:

a. b.

Solution

䊳

a. 6 is common to all three terms:

mentally:

b. is common to both terms:

mentally:

Now try Exercises 7 and 8

䊳

B. Common Binomial Factors and Factoring by Grouping

If the terms of a polynomial have a common binomial factor, it can also be factored

out using the distributive property.

EXAMPLE 2

䊳

Factoring Out a Common Binomial Factor

Factor:

a. b.

Solution

䊳

a. b.

Now try Exercises 9 and 10

䊳

One application of removing a binomial factor involves factoring by grouping.

At ﬁrst glance, the expression appears unfactorable. But by group-

ing the terms (applying the associative property), we can remove a monomial factor

from each subgroup, which then reveals a common binomial factor.

This grouping of terms must take into account any sign changes and common fac-

tors, as seen in Example 3. Also, it will be helpful to note that a general four-term poly-

nomial is factorable by grouping only if .

EXAMPLE 3

䊳

Factoring by Grouping

Factor

Solution

䊳

Notice that all four terms have a common factor of 3. Begin by factoring it out.

original polynomial

factor out 3

group remaining terms

factor common

monomial

factor common

binomial

Now try Exercises 11 and 12

䊳

⫽ 31t ⫹ 521t

⫺ 22

⫽ 33t

1t ⫹ 52⫺ 21t ⫹ 524

⫽ 31t

⫹ 5t

⫺ 2t ⫺ 102

⫽ 31t

⫹ 5t

⫺ 2t ⫺ 102

⫹ 15t

⫺ 6t ⫺ 30

⫹ 15t

⫺ 6t ⫺ 30.

AD ⫽ BCA ⫹ B ⫹ C ⫹ D

⫽ 1x ⫹ 221x

⫹ 32

⫹ 2x

⫹ 3x ⫹ 6 ⫽ x

1x ⫹ 22⫹ 31x ⫹ 22

⫹ 2x

⫹ 3x ⫹ 6

⫽ 1x ⫺ 221x

⫺ 32⫽ 1x ⫹ 321x

⫹ 52

1x ⫺ 22⫺ 31x ⫺ 221x ⫹ 32x

⫹ 1x ⫹ 325

1x ⫺ 22⫺ 31x ⫺ 221x ⫹ 32x

⫹ 1x ⫹ 325

⫽ x

⫹ 12

⫹ x

1 x

⫹ x

⫽ 612x

⫹ 3xy ⫺ 5y2

⫹ 6

3xy ⫺ 6

5y 12x

⫹ 18xy ⫺ 30y

⫹ x

12x

⫹ 18xy ⫺ 30y

A. You’ve just seen how

we can factor out the greatest

common factor

cob19545_chR_040-053.qxd 7/28/10 2:37 PM Page 40

When asked to factor an expression, ﬁrst look for common factors. The resulting

expression will be easier to work with and help ensure the ﬁnal answer is written in

completely factored form. If a four-term polynomial cannot be factored as written, try

rearranging the terms to ﬁnd a combination that enables factoring by grouping.

C. Factoring Quadratic Polynomials

A quadratic polynomial is one that can be written in the form where

a, b, and One common form of factoring involves quadratic trinomials

such as and While we know

and using F-O-I-L, how can we

factor these trinomials without seeing the original expression in advance? First, it helps

to place the trinomials in two families—those with a leading coefﬁcient of 1 and those

with a leading coefﬁcient other than 1.

, where

When the only factor pair for (other than is and the ﬁrst term in

each binomial will be x: (x )(x ). The following observation helps guide us to

the complete factorization. Consider the product

F-O-I-L

distributive property

Note the last term is the product ab (the lasts), while the coefﬁcient of the middle

term is (the sum of the outers and inners). Since the last term of is

7 and the coefﬁcient of the middle term is we are seeking two numbers with a

product of positive 7 and a sum of negative 8. The numbers are and so the fac-

tored form is It is also helpful to note that if the constant term is posi-

tive, the binomials will have like signs, since only the product of like signs is positive.

If the constant term is negative, the binomials will have unlike signs, since only the

product of unlike signs is negative. This means we can use the sign of the linear term

(the term with degree 1) to guide our choice of factors.

Factoring Trinomials with a Leading Coefﬁcient of 1

If the constant term is positive, the binomials will have like signs:

or ,

to match the sign of the linear (middle) term.

If the constant term is negative, the binomials will have unlike signs:

with the larger factor placed in the binomial

whose sign matches the linear (middle) term.

EXAMPLE 4

䊳

Factoring Trinomials

Factor these expressions:

a. b.

Solution

䊳

a. First rewrite the trinomial in standard form as For

the constant term is positive so the binomials will have like

signs. Since the linear term is negative,

like signs, both negative

1⫺821⫺32⫽ 24; ⫺8 ⫹ 1⫺32⫽⫺11 ⫽⫺11x ⫺ 821x ⫺ 32

⫺11x

⫺ 11x ⫹ 242⫽⫺11x ⫺ 21x ⫺ 2

⫺ 11x ⫹ 24,

⫺11x

⫺ 11x ⫹ 242.

⫺ 10 ⫺ 3x⫺x

⫹ 11x ⫺ 24

1x ⫹ 21x ⫺ 2,

1x ⫺ 21x ⫺ 21x ⫹ 21x ⫹ 2

1x ⫺ 721x ⫺ 12.

⫺1,⫺7

⫺8,

⫺ 8x ⫹ 7a ⫹ b

⫽ x

⫹ 1a ⫹ b2x ⫹ ab

1x ⫹ b21x ⫹ a2⫽ x

⫹ ax ⫹ bx ⫹ ab

1x ⫹ b21x ⫹ a2:

a ⫽ 1,

a ⴝ 1ax

ⴙ bx ⴙ c

12x ⫺ 321x ⫺ 52⫽ 2x

⫺ 13x ⫹ 15x

⫹ 7x ⫹ 10

1x ⫹ 521x ⫹ 22⫽2x

⫺ 13x ⫹ 15.x

⫹ 7x ⫹ 10

a ⫽ 0.c 僆⺢

⫹ bx ⫹ c,

R–41 Section R.4 Factoring Polynomials and Solving Polynomial Equations by Factoring 41

College Algebra Graphs & Models—

B. You’ve just seen how

we can factor common

binomial factors and factor by

grouping

cob19545_chR_040-053.qxd 7/28/10 2:37 PM Page 41

42 CHAPTER R A Review of Basic Concepts and Skills R–42

College Algebra Graphs & Models—

b. First rewrite the trinomial in standard form as The constant

term is negative so the binomials will have unlike signs. Since the linear term

is negative,

unlike signs, one positive and one negative

Now try Exercises 13 and 14

䊳

Sometimes we encounter prime polynomials, or polynomials that cannot be fac-

tored. For the factor pairs of 15 are and with neither pair

having a sum of We conclude that is prime.

, where

If the leading coefﬁcient is not one, the possible combinations of outers and inners are

more numerous. Furthermore, the sum of the outer and inner products will change de-

pending on the position of the possible factors. Note that

and result in a different middle

term, even though identical numbers were used.

To factor note the constant term is positive so the binomials must

have like signs. The negative linear term indicates these signs will be negative. We then

list possible factors for the ﬁrst and last terms of each binomial, then sum the outer and

inner products.

⫺ 13x ⫹ 15,

12x ⫹ 921x ⫹ 32⫽ 2x

⫹ 15x ⫹ 272x

⫹ 21x ⫹ 27

12x ⫹ 321x ⫹ 92⫽

a ⴝ 1ax

ⴙ bx ⴙ c

⫹ 9x ⫹ 15⫹9.

5,1

15x

⫹ 9x ⫹ 15,

⫽ 1x ⫹ 221x ⫺ 52

⫺ 3x ⫺ 10 ⫽ 1x ⫹ 21x ⫺ 2

⫺ 3x ⫺ 10.

As you can see, only possibility 3 yields a linear term of and the correct fac-

torization is then With practice, this trial-and-error process can be

completed very quickly.

If the constant term is negative, the number of possibilities can be reduced by ﬁnd-

ing a factor pair with a sum or difference equal to the absolute value of the linear co-

efﬁcient, as we can then arrange the sign in each binomial to obtain the needed result

as shown in Example 5.

EXAMPLE 5

䊳

Factoring a Trinomial Using Trial and Error

Factor .

Solution

䊳

Note the constant term is negative (binomials will have unlike signs) and .

The factors of 35 are and Two possible ﬁrst terms are: (6z )(z )

and (3z )(2z ), and we begin with 5 and 7 as factors of 35.

7.1

冟

⫺11

冟

⫽ 11

⫺ 11z ⫺ 35

12x ⫺ 321x ⫺ 52.

⫺13x,

is placed in the second binomial;

1221⫺52⫽⫺10; 2 ⫹ 1⫺52⫽⫺3

5 7 2, 5

Possible First and Last Terms Sum of

for and 15 Outers and Inners

4. ⫺6x ⫺ 5x ⫽⫺11x12x ⫺ 521x ⫺ 32

d⫺10x ⫺ 3x ⫽⫺13x12x ⫺ 321x ⫺ 52

⫺2x ⫺ 15x ⫽⫺17x12x ⫺ 1521x ⫺ 12

⫺30x ⫺ 1x ⫽⫺31x12x ⫺ 121x ⫺ 152

Outer and Inner Outer and Inner

(6z )(z ) Products (3z )(2z ) Products

Sum Difference Sum Difference

1. (6z 5)(z 7) 42z ⫹ 5z 42z ⫺ 5z 3. (3z 5)(2z 7) 21z ⫹ 10z 21z ⫺ 10z

47z 37z 31z 11z

2. (6z 7)(z 5) 30z ⫹ 7z 30z ⫺ 7z 4. (3z 7)(2z 5) 15z ⫹ 14z 15z ⫺ 14z

37z 23z 29z 1z

WORTHY OF NOTE

The number of trials needed to

factor a polynomial can also be

reduced by noting that the two

terms in any binomial cannot share

a common factor (all common

factors are removed in a preliminary

step).

cob19545_chR_040-053.qxd 11/23/10 6:33 PM Page 42

Since possibility 3 yields a linear term of 11z, we need not consider other factors

of 35 and write the factored form as The

signs can then be arranged to obtain a middle term of

✓.

Now try Exercises 15 and 16

䊳

D. Factoring Special Forms and Quadratic Forms

Next we consider methods to factor each of the special products we encountered in

Section R.2.

The Difference of Two Squares

Multiplying and factoring are inverse processes. Since we

know that In words, the difference of two squares will

factor into a binomial and its conjugate. To ﬁnd the terms of the factored form, rewrite

each term in the original expression as a square:

Factoring the Difference of Two Perfect Squares

Given any expression that can be written in the form

Note that the sum of two perfect squares cannot be factored using real num-

bers (the expression is prime). As a reminder, always check for a common factor ﬁrst

and be sure to write all results in completely factored form. See Example 6(c).

EXAMPLE 6

䊳

Factoring the Difference of Two Perfect Squares

Factor each expression completely.

a. b. c. d. e.

Solution

䊳

a. write as a difference of squares

b. is prime.

factor out

write as a difference of squares

d. write as a difference of squares

write as a difference of squares ( is prime)

result

e. write as a difference of squares

Now try Exercises 17 and 18

䊳

Perfect Square Trinomials

Since we know that In words,

a perfect square trinomial will factor into a binomial square. To use this idea effectively,

we must learn to identify perfect square trinomials. Note that the ﬁrst and last terms of

are the squares of x and 7, and the middle term is twice the product of

these two terms: These are the characteristics of a perfect square trinomial.217x2⫽ 14x.

⫹ 14x ⫹ 49

⫹ 14x ⫹ 49 ⫽ 1x ⫹ 72

.1x ⫹ 72

⫽ x

⫹ 14x ⫹ 49,

⫺ B

⫽ 1A ⫹ B21A ⫺ B2 ⫽ 1x ⫹ 1721x ⫺ 172

⫺ 7 ⫽ 1x2

⫺ 1172

⫽ 1z

⫹

21z ⫹

21z ⫺

⫹

⫽ 1z

⫹

23z

⫺ 1

⫺ B

⫽ 1A ⫹ B21A ⫺ B2 ⫽ 1z

⫹

21z

⫺

⫽ 1z

⫺ 1

⫺ B

⫽ 1A ⫹ B21A ⫺ B2 ⫽⫺31n ⫹ 421n ⫺ 42

⫽⫺33n

⫺ 142

⫺3 ⫺3n

⫹ 48 ⫽⫺31n

⫺ 162

⫹ 49

⫺ B

⫽ 1A ⫹ B21A ⫺ B2 ⫽ 12w ⫹ 9212w ⫺ 92

4 w

⫺ 81 ⫽ 12w2

⫺ 9

⫺ 7z

⫺

⫺3n

⫹ 48v

⫹ 494w

⫺ 81

⫹ B

⫺ B

⫽ 1A ⫹ B21A ⫺ B2

⫺ B

⫺ 49 ⫽ 1x ⫺ 721x ⫹ 72.

1x ⫺ 721x ⫹ 72⫽ x

⫺ 49,

⫺21z ⫹ 10z ⫽⫺11z

⫺11z: 13z ⫹ 5212z ⫺ 72,

⫺ 11z ⫺ 35 ⫽ 13z

5212z

72.

R–43 Section R.4 Factoring Polynomials and Solving Polynomial Equations by Factoring 43

College Algebra Graphs & Models—

C. You’ve just seen how

we can factor quadratic

polynomials

WORTHY OF NOTE

In an attempt to factor a sum of

two perfect squares, say

let’s list all possible binomial

factors. These are (1)

(2) and

(3) Note that (1) and

(2) are the binomial squares

and with each

product resulting in a “middle”

term, whereas (3) is a binomial

times its conjugate, resulting in a

difference of squares: With

all possibilities exhausted, we

conclude that the sum of two

squares is prime!

⫺ 49.

1v ⫺ 72

,1v ⫹ 72

1v ⫹ 721v ⫺ 72.

1v ⫺ 721v ⫺ 72,

1v ⫹ 721v ⫹ 72,

⫹ 49,

cob19545_chR_040-053.qxd 7/28/10 2:38 PM Page 43

44 CHAPTER R A Review of Basic Concepts and Skills R–44

College Algebra Graphs & Models—

Factoring Perfect Square Trinomials

Given any expression that can be written in the form

EXAMPLE 7

䊳

Factoring a Perfect Square Trinomial

Factor

Solution

䊳

check for common factors:

factor out 3

For the remaining trinomial

1. Are the ﬁrst and last terms perfect squares?

and ✓ Yes.

2. Is the linear term twice the product of and 1?

✓ Yes.

Factor as a binomial square:

This shows

Now try Exercises 19 and 20

䊳

12m

⫺ 12m

⫹ 3m ⫽ 3m12m ⫺ 12

⫺ 4m ⫹ 1 ⫽ 12m ⫺ 12

1 ⫽ 4m

1 ⫽ 112

⫽ 12m2

⫺ 4m ⫹ 1 p

⫽ 3m14m

⫺ 4m ⫹ 12

GCF ⫽ 3m12m

⫺ 12m

⫹ 3m

12m

⫺ 12m

⫹ 3m.

⫺ 2AB ⫹ B

⫽ 1A ⫺ B2

⫹ 2AB ⫹ B

⫽ 1A ⫹ B2

⫾ 2AB ⫹ B

CAUTION

䊳

As shown in Example 7, be sure to include the GCF in your ﬁnal answer. It is a common

error to “leave the GCF behind.”

In actual practice, these calculations can be performed mentally, making the

process much more efﬁcient.

Sum or Difference of Two Perfect Cubes

Recall that the difference of two perfect squares is factorable, but the sum of two perfect

squares is prime. In contrast, both the sum and difference of two perfect cubes are fac-

torable. For either or we have the following:

1. Each will factor into the product of a binomial ( )( )

and a trinomial:

binomial trinomial

2. The terms of the binomial are the quantities

being cubed: (AB)( )

3. The terms of the trinomial are the square of A,

the product AB, and the square of B, respectively: (AB)(A

AB B

)

4. The binomial takes the same sign as the original

expression ( )( )

5. The middle term of the trinomial takes the

opposite sign of the original expression

(the last term is always positive): ( )( )

Factoring the Sum or Difference of Two Perfect Cubes: A

⫾ B

2. A

⫺ B

⫽ 1A ⫺ B21A

⫹ AB ⫹ B

⫹ B

⫽ 1A ⫹ B21A

⫺ AB ⫹ B

⫿ AB ⫹ B

A ⫾ B

AB B

A ⫾ B

⫺ B

⫹ B

cob19545_chR_040-053.qxd 7/28/10 2:38 PM Page 44

EXAMPLE 8

䊳

Factoring the Sum and Difference of Two Perfect Cubes

Factor completely:

a. b.

Solution

䊳

a. write terms as perfect cubes

Use factoring template

and

factoring template

and

simplify

factored form

The results for parts (a) and (b) can be checked using multiplication.

Now try Exercises 21 and 22

䊳

Quadratic Forms and u-Substitution

For any quadratic expression in standard form, the degree of the

leading term is twice the degree of the middle term. Generally, a trinomial is in

quadratic form if it can be written as where the parentheses

“hold” the same factors. The equation is in quadratic form

since In many cases, we can factor these expressions

using a placeholder substitution that transforms them into a more recognizable

form. In a study of algebra, the letter “u” often plays this role. If we let u represent

the expression becomes which can be

factored into After “unsubstituting” (replace u with ), we have

EXAMPLE 9

䊳

Factoring a Quadratic Form

Write in completely factored form:

Solution

䊳

Expanding the binomials would produce a fourth-degree polynomial that would

be very difﬁcult to factor. Instead we note the expression is in quadratic

form. Letting u represent (the variable part of the “middle” term),

becomes

factor

To ﬁnish up, write the expression in terms of x, substituting for u.

substitute for

The resulting trinomials can be further factored.

Now try Exercises 23 and 24

䊳

It is well known that information is retained longer and used more effectively

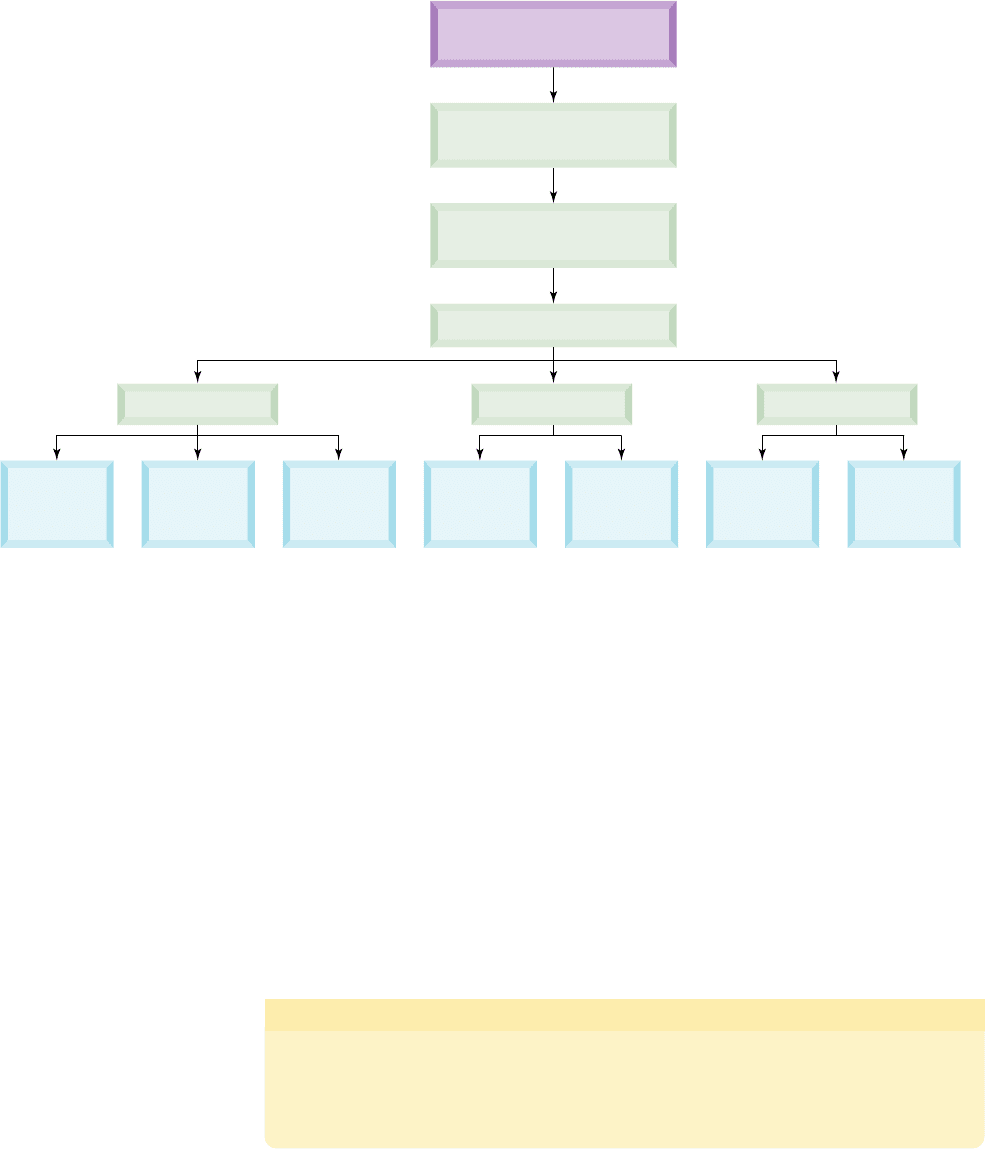
when it’s placed in an organized form. The “factoring flowchart” provided in Fig-

ure R.4 offers a streamlined and systematic approach to factoring and the concepts in-

volved. However, with some practice the process tends to “ﬂow” more naturally than

following a chart, with many of the decisions becoming automatic.

⫺ 2x ⫹ 1 ⫽ 1x ⫺ 12

⫽ 1x ⫺ 321x ⫹ 121x ⫺ 12

⫺ 2x⫽ 1x

⫺ 2x ⫺ 321x

⫺ 2x ⫹ 12

⫺ 2x

⫺ 2u ⫺ 3 ⫽ 1u ⫺ 321u ⫹ 12

⫺ 2u ⫺ 3.21x

⫺ 2x2⫺ 31x

⫺ 2x2

⫺

⫺ 2x

⫺ 2x2

⫺ 21x

⫺ 2x2⫺ 3.

⫺ 921x

⫺ 42⫽ 1x ⫹ 321x ⫺ 321x ⫹ 221x ⫺ 22.

1u ⫺ 921u ⫺ 42.

⫺ 13u ⫹ 36,1x

⫺ 131x

2⫹ 36x

⫺ 131x

2⫹ 36 ⫽ 0.

⫺ 13x

⫹ 36 ⫽ 0

⫹ b1

2⫹ c,

⫹ bx ⫹ c

1 ⫺5m

n ⫹ 40n

⫽⫺5n1m ⫺ 2n21m

⫹ 2mn ⫹ 4n

⫽ 1m ⫺ 2n21m

⫹ 2mn ⫹ 4n

B S 2nA S m m

⫺ 12n2

⫽ 1m ⫺ 2n23m

⫹ m12n2⫹ 12n2

Use A

⫺ B

⫽ 1A ⫺ B21A

⫹ AB ⫹ B

⫽⫺5n3m

⫺ 12n2

⫺5m

n ⫹ 40n

⫽⫺5n1m

⫺ 8n

B S 5A S x x

⫹ 5

⫽ 1x ⫹ 521x

⫺ 5x ⫹ 252

⫹ B

⫽ 1A ⫹ B21A

⫺ AB ⫹ B

⫹ 125 ⫽ x

⫹ 5

⫺5m

n ⫹ 40n

⫹ 125

R–45 Section R.4 Factoring Polynomials and Solving Polynomial Equations by Factoring 45

College Algebra Graphs & Models—

check for common

factors 1GCF ⫽⫺5n2

write terms as perfect cubes

D. You’ve just seen how

we can factor special forms

and quadratic forms

cob19545_chR_040-053.qxd 7/28/10 2:38 PM Page 45

46 CHAPTER R A Review of Basic Concepts and Skills R–46

College Algebra Graphs & Models—

For additional practice with these ideas, see Exercises 25 through 52.

E. Polynomial Equations and the Zero Product Property

The ability to solve linear and quadratic equations is the foundation on which a large

percentage of our future studies are built. Both are closely linked to the solution of

other equation types, as well as to the graphs of these equations.

In standard form, linear and quadratic equations have a known number of

terms, so we commonly represent their coefficients using the early letters of the

alphabet, as in However, these equations belong to the larger

family of polynomial equations. To write a general polynomial, where the num-

ber of terms is unknown, we often represent the coefficients using subscripts on a

single variable, such as and so on.

Polynomial Equations

A polynomial equation of degree n is one of the form

where are real numbers and

As a prelude to solving polynomial equations of higher degree, we’ll ﬁrst look at

quadratic equations and the zero product property. As before, a quadratic equation is

one that can be written in the form where a, b, and c are real num-

bers and . As written, the equation is in standard form, meaning the terms are

in decreasing order of degree and the equation is set equal to zero.

a ⫽ 0

⫹ bx ⫹ c ⫽ 0,

⫽ 0.a

, a

n⫺1

, p , a

, a

⫹ a

n⫺1

⫹

⫹ a

⫽ 0

, a

⫹ bx ⫹ c ⫽ 0.

• Can any result be factored further? • Polynomials that cannot be factored are said to be prime.

Two Four

Standard Form:

decreasing order of degree

Greatest Common Factor

(positive leading coefficient)

Number of Terms

Factoring

Polynomials

Advanced

methods

(Section 4.2)

Difference

of cubes

Difference

of squares

Factor by

grouping

Sum

of cubes

Trinomials

(a ⫽ 1)

Trinomials

(a ⫽ 1)

Three

Figure R.4

cob19545_chR_040-053.qxd 11/22/10 10:56 AM Page 46

Quadratic Equations

A quadratic equation can be written in the form

with and

Notice that a is the leading coefﬁcient, b is the coefﬁcient of the linear (ﬁrst

degree) term, and c is a constant. All quadratic equations have degree two, but can have

one, two, or three terms. The equation is a quadratic equation with two

terms, where and

EXAMPLE 10

䊳

Determining Whether an Equation Is Quadratic

State whether the given equation is quadratic. If yes, identify coefﬁcients a, b, and c.

a. b. c.

d. e.

Solution

䊳

Now try Exercises 53 through 64

䊳

With quadratic and other polynomial equations, we generally cannot isolate the

variable on one side using only properties of equality, because the variable is raised to

different powers. Instead we attempt to solve the equation by factoring and applying

the zero product property.

Zero Product Property

If A and B represent real numbers or real-valued expressions

and

then or .

In words, the property says, If the product of any two (or more) factors is equal to

zero, then at least one of the factors must be equal to zero. We can use this property to

solve higher degree equations after rewriting them in terms of equations with lesser

degree. As with linear equations, values that make the original equation true are called

solutions or roots of the equation.

B ⫽ 0A ⫽ 0

B ⫽ 0,

0.8x

⫽ 0z

⫺ 2z

⫹ 7z ⫽ 8

⫺3

x ⫹ 5 ⫽ 0z ⫺ 12 ⫺ 3z

⫽ 02x

⫺ 18 ⫽ 0

c ⫽⫺81.a ⫽ 1, b ⫽ 0,

⫺ 81 ⫽ 0

a ⫽ 0.a, b, c 僆⺢,

⫹ bx ⫹ c ⫽ 0,

R–47 Section R.4 Factoring Polynomials and Solving Polynomial Equations by Factoring 47

College Algebra Graphs & Models—

Standard Form Quadratic Coefﬁcients

a. yes, deg 2

b. yes, deg 2

c. no, deg 1 (linear equation)

d. no, deg 3 (cubic equation)

e. yes, deg 2 c ⫽ 0b ⫽ 0a ⫽ 0.80.8x

⫽ 0

⫺ 2z

⫹ 7z ⫺ 8 ⫽ 0

⫺3

x ⫹ 5 ⫽ 0

c ⫽⫺12b ⫽ 1a ⫽⫺3⫺3z

⫹ z ⫺ 12 ⫽ 0

c ⫽⫺18b ⫽ 0a ⫽ 22x

⫺ 18 ⫽ 0

WORTHY OF NOTE

The word quadratic comes from the

Latin word quadratum, meaning

square. The word historically refers

to the “four sidedness” of a square,

but mathematically to the area of a

square. Hence its application to

polynomials of the form

, where the variable of

the leading term is squared.

⫹ bx ⫹ c

cob19545_chR_040-053.qxd 7/28/10 2:38 PM Page 47

48 CHAPTER R A Review of Basic Concepts and Skills R–48

College Algebra Graphs & Models—

EXAMPLE 11

䊳

Solving Equations Using the Zero Product Property

Solve by writing the equations in factored form and applying the zero product property.

a. b. c.

Solution

䊳

a. given equation

standard form

factor

set factors equal to zero (zero product property)

result

b. given equation

standard form

factor

set factors equal to zero (zero product property)

result

c. given equation

standard form

factor

set factors equal to zero (zero product property)

result

This equation has only the solution which we call a repeated root.

Now try Exercises 65 through 88

䊳

x ⫽

2x ⫺ 3 ⫽ 0

12x ⫺ 3212x ⫺ 32⫽ 0

4 x

⫺ 12x ⫹ 9 ⫽ 0

4 x

⫽ 12x ⫺ 9

x ⫽⫺

x ⫽ 3

2x ⫹ 1 ⫽ 0

x ⫺ 3 ⫽ 0

12x ⫹ 121x ⫺ 32⫽ 0

2 x

⫺ 5x ⫺ 3 ⫽ 0

⫺5x ⫹ 2x

⫽ 3

x ⫽ 0

x ⫽

x ⫽ 0

3x ⫺ 5 ⫽ 0

x13x ⫺ 52⫽ 0

3 x

⫺ 5x ⫽ 0

3 x

⫽ 5x

⫽ 12x ⫺ 9⫺5x ⫹ 2x

⫽ 33x

⫽ 5x

CAUTION

䊳

Consider the equation While the left-hand side is factorable, the result

is and ﬁnding a solution becomes a “guessing game” because the

equation is not set equal to zero. If you misapply the zero factor property and say that

or the “solutions” are or which are both incorrect!

After subtracting 12 from both sides, becomes

giving with solutions or x ⫽⫺3.x ⫽ 51x ⫺ 521x ⫹ 32⫽ 0

⫺ 2x ⫺ 15 ⫽ 0x

⫺ 2x ⫺ 3 ⫽ 12

x ⫽ 11,x ⫽ 15x ⫹ 1 ⫽ 12,x ⫺ 3 ⫽ 12

1x ⫺ 321x ⫹ 12⫽ 12

⫺ 2x ⫺ 3 ⫽ 12.

EXAMPLE 12

䊳

Solving Polynomials by Factoring

Solve by factoring:

Solution

䊳

given equation

standard form

common factor is 2

factored form

zero product property

result—solve for

Substituting these values into the original equation veriﬁes they are solutions.

Now try Exercises 89 through 92

䊳

x ⫽ 0

x ⫽

⫺5

x ⫽ 4

2 x ⫽ 0

2 x ⫹ 5 ⫽ 0

x ⫺ 4 ⫽ 0

2 x12x ⫹ 521x ⫺ 42⫽ 0

2 x 12x

⫺ 3x ⫺ 202⫽ 0

4 x

⫺ 6x

⫺ 40x ⫽ 0

4 x

⫺ 40x ⫽ 6x

Example 12 reminds us that in the process of factoring polynomials, there may be

a common monomial factor. This factor is also set equal to zero in the solution process

(if the monomial is a constant, no solution is generated).

cob19545_chR_040-053.qxd 7/28/10 2:38 PM Page 48

R–49 Section R.4 Factoring Polynomials and Solving Polynomial Equations by Factoring 49

College Algebra Graphs & Models—

2. If a polynomial will not factor, it is said to be a(n)

polynomial.

3. The difference of two perfect squares always

factors into the product of a(n) and its

4. The expression is said to be a(n)

trinomial, since its factored

form is a perfect (binomial) square.

⫹ 6x ⫹ 9

5. Discuss/Explain why

is not written in

completely factored form, then rewrite it so it is

factored completely.

12x ⫹ 6212x ⫺ 624x

⫺ 36 ⫽

6. Discuss/Explain why is factorable, but

is not. Demonstrate by writing in

factored form, and by exhausting all possibilities for

to show it is prime.x

⫹ 64

⫹ 64a

⫹ b

䊳

CONCEPTS AND VOCABULARY

Fill in each blank with the appropriate word or phrase. Carefully reread the section, if necessary.

R.4 EXERCISES

1. To factor an expression means to rewrite the

expression as an equivalent .

EXAMPLE 13

䊳

Solving Higher Degree Equations

Solve each equation by factoring.

a. b.

Solution

䊳

a. original equation

standard form; factor by grouping

remove common factors from each group

factor common binomial

factored form

zero product property

solve

The solutions are and

b. The equation appears to be in quadratic form and we begin by substituting u

for x

and u

for x

original equation

substitute

for

and

for

factored form

zero product property

substitute

for

factor

zero product property

The solutions are and

Now try Exercises 93 through 100

䊳

In Examples 12 and 13, we were able to solve higher degree polynomial equations

by “breaking them down” into linear and quadratic forms. This basic idea can be

applied to other kinds of equations as well.

x ⫽ 1.x ⫽⫺3, x ⫽ 3, x ⫽⫺1,

x ⫽⫺3 or x ⫽ 3

x ⫽⫺1 or x ⫽ 1

1x ⫹ 321x ⫺ 32⫽ 0

1x ⫹ 121x ⫺ 12⫽ 0

⫺ 9 ⫽ 0

⫺ 1 ⫽ 0

u ⫺ 9 ⫽ 0

u ⫺ 1 ⫽ 0

1u ⫺ 921u ⫺ 12⫽ 0

⫺ 10u ⫹ 9 ⫽ 0

⫺ 10x

⫹ 9 ⫽ 0

x ⫽ 2.x ⫽ 5, x ⫽⫺2,

x ⫽ 5

x ⫽⫺2

x ⫽ 2

x ⫺ 5 ⫽ 0

x ⫹ 2 ⫽ 0

x ⫺ 2 ⫽ 0

1x ⫺ 521x ⫹ 221x ⫺ 22⫽ 0

1x ⫺ 521x

⫺ 42⫽ 0

1x ⫺ 52⫺ 41x ⫺ 52⫽ 0

⫺ 5x

⫺ 4x ⫹ 20 ⫽ 0

⫺ 4x ⫹ 20 ⫽ 5x

⫺ 10x

⫹ 9 ⫽ 0x

⫺ 4x ⫹ 20 ⫽ 5x

E. You’ve just seen how

we can solve polynomial

equations by factoring

cob19545_chR_040-053.qxd 11/22/10 10:58 AM Page 49