Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models
Подождите немного. Документ загружается.

60 CHAPTER R A Review of Basic Concepts and Skills R–60
College Algebra Graphs & Models—
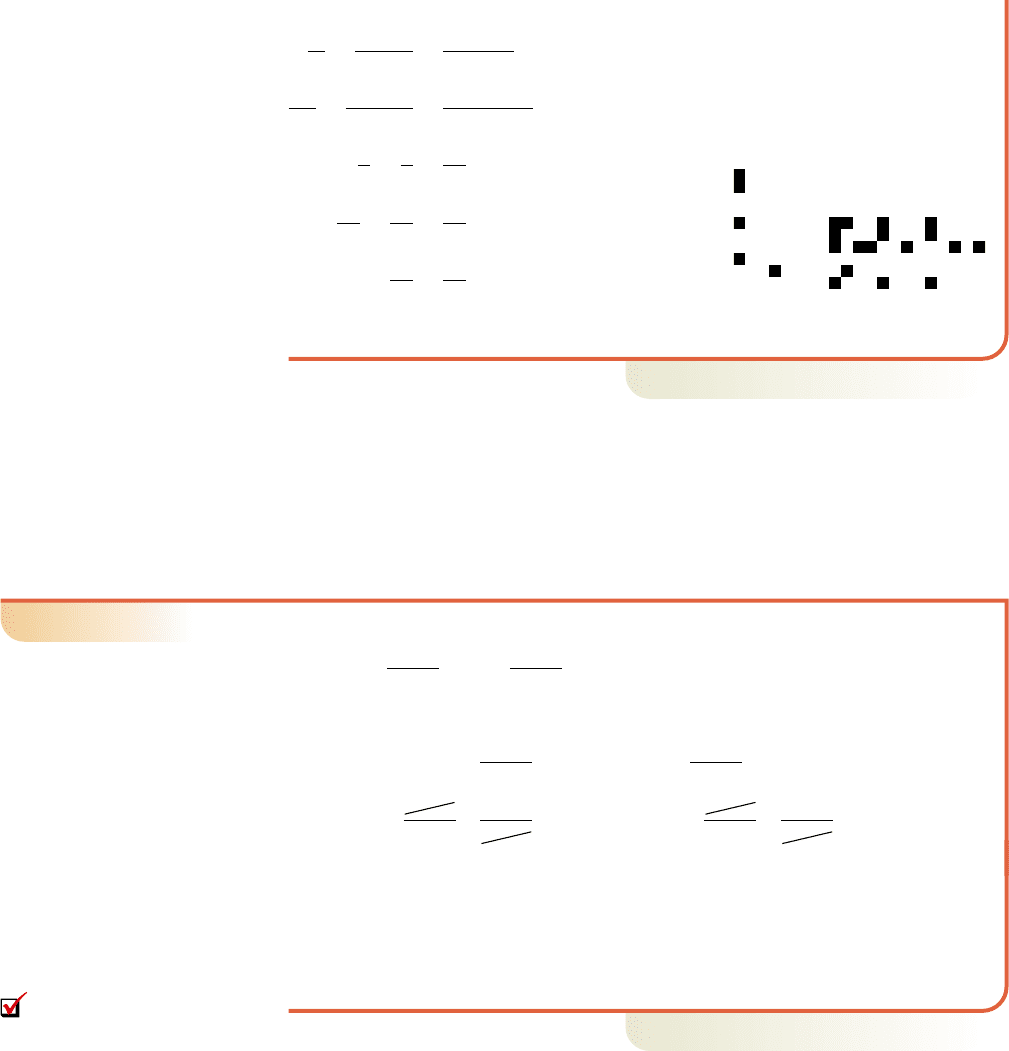
Checking by substitution we have:
original equation
substitute 6 for
m
simplify
common denominator
✓ result
A calculator check is shown in the figure.
Now try Exercises 75 through 80
Multiplying both sides of an equation by a variable sometimes introduces a solu-
tion that satisfies the resulting equation, but not the original equation—the one we’re
trying to solve. Such “solutions” are called extraneous roots and illustrate the need to
check all apparent solutions in the original equation. In the case of rational equations,
we are particularly aware that any value that causes a zero denominator is outside the
domain and cannot be a solution.
EXAMPLE 9
Solving a Rational Equation
Solve:
Solution
The LCD is where
denominators are eliminated
set equation equal to zero
factor
zero factor property
Checking shows is an extraneous root, and is the only valid solution.
Now try Exercises 81 through 86
x ⫽ 5x ⫽ 3
x ⫽ 3
or
x ⫽ 5
1x ⫺ 321x ⫺ 52⫽ 0
x
2
⫺ 8x ⫹ 15 ⫽ 0
x
2
⫺ 3x ⫹ 12 ⫽ x ⫺ 3 ⫹ 4x
1x ⫺ 32x ⫹ a
x ⫺ 3
1
ba
12
x ⫺ 3
b⫽ 1x ⫺ 32112⫹ a
x ⫺ 3
1
ba
4x
x ⫺ 3
b
1x ⫺ 32ax ⫹
12
x ⫺ 3
b⫽ 1x ⫺ 32a1 ⫹
4x
x ⫺ 3
b
x ⫽ 3.x ⫺ 3,
x ⫹
12
x ⫺ 3
⫽ 1 ⫹
4x
x ⫺ 3
.
2
15
⫽
2
15
5
15
⫺
3
15
⫽
2
15
1
3
⫺
1
5
⫽
4
30
2
162
⫺
1
162⫺ 1
⫽
4
162
2
⫺ 162
2
m
⫺
1
m ⫺ 1
⫽
4
m
2
⫺ m
multiply both
sides by LCD
distribute and
simplify
E. You’ve just seen how we
can solve rational equations
cob19545_chR_054-064.qxd 11/22/10 10:27 AM Page 60

2. A rational expression is in when the
numerator and denominator have no common
factors, other than .
4. Since is prime, the expression
is already written in .
6.
1x ⫹ 32
1x ⫺ 22
1x ⫺ 221x ⫹ 32
⫽ 0
1x ⫹ 32
1x
2
⫹ 92/x
2
⫹ 9
CONCEPTS AND VOCABULARY
Fill in each blank with the appropriate word or phrase. Carefully reread the section, if necessary.
R.5 EXERCISES
1. In simplest form, is equal to
, while is equal to .
3. As with numeric fractions, algebraic fractions
require a for addition and
subtraction.
State T or F and discuss/explain your response.
5.
x
x ⫹ 3
⫺
x ⫹ 1
x ⫹ 3
⫽
1
x ⫹ 3
1a ⫺ b2/1b ⫺ a2
1a ⫺ b2/1a ⫺ b2
DEVELOPING YOUR SKILLS
Reduce to lowest terms.
7. a. b.
8. a. b.
9. a. b.
10. a. b.
11. a. b.
12. a. b.
13. a. b.
c. d.
14. a. b.
c. d.
15. a. b.
c. d.
mn
2
⫹ n
2
⫺ 4m ⫺ 4
mn ⫹ n ⫹ 2m ⫹ 2
x
3
⫹ 8
x
2
⫺ 2x ⫹ 4
6x
2
⫹ x ⫺ 15
4x
2
⫺ 9
2n
3
⫹ n
2
⫺ 3n
n
3
⫺ n
2
w
4
⫺ w
4
v
w
3
v ⫺ w
3
n
2
⫺ 4
2 ⫺ n
⫺5v ⫹ 20
25
5m
⫺3
n
5
⫺10mn
2
m
3
n ⫺ m
3
m
4
⫺ m
4
n
y
2
⫺ 9
3 ⫺ y
7x ⫹ 21
63
⫺12a
3
b
5
4a
2
b
⫺4
u
2
⫺ 10u ⫹ 25
25 ⫺ u
2
v
2
⫺ 3v ⫺ 28
49 ⫺ v
2
5 ⫺ x
x ⫺ 5
x ⫺ 7
7 ⫺ x
m
2
⫹ 3m ⫺ 4
m
2
⫺ 4m
r
2
⫹ 3r ⫺ 10
r
2
⫹ r ⫺ 6
a
2
⫹ 3a ⫺ 28
a
2
⫺ 49
x
2
⫺ 5x ⫺ 14
x
2
⫹ 6x ⫺ 7
3x ⫺ 18
6x
2
⫺ 12x
x ⫺ 4
⫺7x ⫹ 28
2x ⫹ 6
4x
2
⫺ 8x
a ⫺ 7
⫺3a ⫹ 21
16. a. b.
c. d.
Compute as indicated. Write final results in lowest terms.
17.
18.
19.
20.
21.
22.
23.
24.
25.
a
2
⫹ a
a
2
⫺ 3a
#
3a ⫺ 9
2a ⫹ 2
5b ⫺ 10
7b ⫺ 28
⫼
2 ⫺ b
5b ⫺ 20
3x ⫺ 9
4x ⫹ 12
⫼
3 ⫺ x
5x ⫹ 15
a
2
⫹ 3a ⫺ 28
a
2
⫹ 5a ⫺ 14
⫼
a
3
⫺ 4a
2
a
3
⫺ 8
p
3
⫺ 64
p
3
⫺ p
2
⫼
p
2
⫹ 4p ⫹ 16
p
2
⫺ 5p ⫹ 4
6v
2
⫹ 23v ⫹ 21
4v
2
⫺ 4v ⫺ 15
#
4v
2
⫺ 25
3v ⫹ 7
x
2
⫺ 7x ⫺ 18
x
2
⫺ 6x ⫺ 27
#
2x
2
⫹ 7x ⫹ 3
2x
2
⫹ 5x ⫹ 2
b
2
⫹ 5b ⫺ 24
b
2
⫺ 6b ⫹ 9
#
b
b
2
⫺ 64
a
2
⫺ 4a ⫹ 4
a
2
⫺ 9
#
a
2
⫺ 2a ⫺ 3
a
2
⫺ 4
ax
2
⫺ 5x
2
⫺ 3a ⫹ 15
ax ⫺ 5x ⫹ 5a ⫺ 25
12y
2
⫺ 13y ⫹ 3
27y
3
⫺ 1
5p
2
⫺ 14p ⫺ 3
5p
2
⫹ 11p ⫹ 2
x
3
⫹ 4x
2
⫺ 5x
x
3
⫺ x
R–61 Section R.5 Rational Expressions and Equations 61
College Algebra Graphs & Models—
cob19545_chR_054-064.qxd 7/28/10 2:45 PM Page 61

26.
27
.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42. a
4x
2
⫺ 25
x
2
⫺ 11x ⫹ 30
⫼
2x
2
⫺ x ⫺ 15
x
2
⫺ 9x ⫹ 18
b
#
4x
2
⫹ 25x ⫺ 21
12x
2
⫺ 5x ⫺ 3
4n
2
⫺ 1
12n
2
⫺ 5n ⫺ 3
#
6n
2
⫹ 5n ⫹ 1
2n
2
⫹ n
#
12n
2
⫺ 17n ⫹ 6
6n
2
⫺ 7n ⫹ 2
p
3
⫹ p
2
⫺ 49p ⫺ 49
p
2
⫹ 6p ⫺ 7
⫼
p
2
⫹ p ⫹ 1
p
3
⫺ 1
3a
3
⫺ 24a
2
⫺ 12a ⫹ 96
a
2
⫺ 11a ⫹ 24
⫼
6a
2
⫺ 24
3a
3
⫺ 81
q
2
⫺
9
25
q
2
⫺
1
10
q ⫺
3
10
⫼
q
2
⫹
17
20
q ⫹
3
20
q
2
⫺
1
16
n
2
⫺
4
9
n
2
⫺
13
15
n ⫹
2
15
⫼
n
2
⫹
4
3
n ⫹
4
9
n
2
⫺
1
25
x
2
⫺ 0.25
x
2
⫹ 0.1x ⫺ 0.2
⫼
x
2
⫺ 0.8x ⫹ 0.15
x
2
⫺ 0.16
x
2
⫺ 0.49
x
2
⫹ 0.5x ⫺ 0.14
⫼
x
2
⫺ x ⫹ 0.21
x
2
⫺ 0.09
x
2
⫹ 4x ⫺ 5
x
2
⫺ 5x ⫺ 14
⫼
x
2
⫺ 1
x
2
⫺ 4
#
x ⫹ 1
x ⫹ 5
y ⫹ 3
3y
2
⫹ 9y
#
y
2
⫹ 7y ⫹ 12
y
2
⫺ 16
⫼
y
2
⫹ 4y
y
2
⫺ 4y
18 ⫺ 6x
x
2
⫺ 25
⫼
2x
2
⫺ 18
x
3
⫺ 2x
2
⫺ 25x ⫹ 50
m
2
⫹ 2m ⫺ 8
m
2
⫺ 2m
⫼
m
2
⫺ 16
m
2
2a ⫺ ab ⫹ 7b ⫺ 14
b
2
⫺ 14b ⫹ 49
⫼
ab ⫺ 2a
ab ⫺ 7a
xy ⫺ 3x ⫹ 2y ⫺ 6
x
2
⫺ 3x ⫺ 10
⫼
xy ⫺ 3x
xy ⫺ 5y
1m
2
⫺ 162
#
m
2
⫺ 5m
m
2
⫺ m ⫺ 20
8
a
2
⫺ 25
#
1a
2
⫺ 2a ⫺ 352
p
2
⫺ 36
2p
#
4p
2
2p
2
⫹ 12p
Compute as indicated. Write answers in lowest terms
[recall that a ⴚ b ⴝⴚ1(b ⴚ a)].
43. 44.
45. 46.
47. 48.
49. 50.
51. 52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
Write each term as a rational expression. Then compute
the sum or difference indicated.
63. a. b.
64. a. b. 2y
⫺1
⫺ 13y2
⫺1
3a
⫺1
⫹ 12a2
⫺1
x
⫺2
⫹ 2x
⫺3
p
⫺2
⫺ 5p
⫺1
m ⫺ 4
3m
2
⫺ 11m ⫹ 6
⫹
m
2m
2
⫺ m ⫺ 15
y ⫹ 2
5y
2
⫹ 11y ⫹ 2
⫹
5
y
2
⫹ y ⫺ 6
m ⫹ 2
m
2
⫺ 25
⫺
m ⫹ 6
m
2
⫺ 10m ⫹ 25
2
m
2
⫺ 9
⫹
m ⫺ 5
m
2
⫹ 6m ⫹ 9
⫺2
3a ⫹ 12
⫺
7
a
2
⫹ 4a
3y ⫺ 4
y
2
⫹ 2y ⫹ 1
⫺
2y ⫺ 5
y
2
⫹ 2y ⫹ 1
2x ⫺ 1
x
2
⫹ 3x ⫺ 4
⫺
x ⫺ 5
x
2
⫹ 3x ⫺ 4
1
a ⫹ 4
⫹
a
a
2
⫺ a ⫺ 20
4n
n
2
⫺ 5n
⫺
3
4n ⫺ 20
y ⫹ 1
y
2
⫹ y ⫺ 30
⫺
2
y ⫹ 6
4
x ⫺ 1
⫺ 9
2
m ⫺ 7
⫺ 5
2
4 ⫺ p
2
⫹
p
p ⫺ 2
m
m
2
⫺ 16
⫹
4
4 ⫺ m
3q
q
2
⫺ 49
⫺
3
2q ⫺ 14
4p
p
2
⫺ 36
⫺
2
p ⫺ 6
3
6a
3
b
⫹
5
9ab
3
7
4x
2
y
3
⫺
1
8xy
4
15
16y
⫺
7
2y
2
3
8x
2
⫹
5
2x
62 CHAPTER R A Review of Basic Concepts and Skills R–62
College Algebra Graphs & Models—
cob19545_chR_054-064.qxd 7/28/10 2:46 PM Page 62
Solve each equation. Identify any extraneous roots.
75.
76.
77.
78.
79. 80.
81.
82.
83.
84.
85.
86.
⫺18
6n
2
⫺ n ⫺ 1
⫹
3n
2n ⫺ 1
⫽
4n
3n ⫹ 1
a
2a ⫹ 1
⫺
2a
2
⫹ 5
2a
2
⫺ 5a ⫺ 3
⫽
3
a ⫺ 3
7
p ⫹ 2
⫺
1
p
2
⫹ 5p ⫹ 6
⫽⫺
2
p ⫹ 3
6
n ⫹ 3
⫹
20
n
2
⫹ n ⫺ 6
⫽
5
n ⫺ 2
10
x ⫺ 5
⫹ x ⫽ 1 ⫹
2x
x ⫺ 5
x ⫹
14
x ⫺ 7
⫽ 1 ⫹
2x
x ⫺ 7
3
5x
⫺
1
2x
⫽
1
x
2
1
3y
⫺
1
4y
⫽
1
y
2
4
2y ⫺ 3
⫽
7
3y ⫺ 5
21
a ⫹ 2
⫽
3
a ⫺ 1
3
m ⫹ 3
⫺
5
m
2
⫹ 3m
⫽
1
m
2
x
⫹
1
x ⫹ 1
⫽
5
x
2
⫹ x
Simplify each compound fraction. Use either method.
65. 66.
67. 68.
69. 70.
71. 72.
Rewrite each expression as a compound fraction. Then
simplify using either method.
73. a. b.
74. a. b.
3 ⫹ 2n
⫺1
5n
⫺2
4 ⫺ 9a
⫺2
3a
⫺2
1 ⫹ 2x
⫺2
1 ⫺ 2x
⫺2
1 ⫹ 3m
⫺1
1 ⫺ 3m
⫺1
2
x
2
⫺ 3x ⫺ 10
6
x ⫹ 2
⫺
4
x ⫺ 5
2
y
2
⫺ y ⫺ 20
3
y ⫹ 4
⫺
4
y ⫺ 5
1
y ⫺ 5
⫺
2
5 ⫺ y
3
y ⫺ 5
⫺
2
y
2
3 ⫺ x
⫹
3
x ⫺ 3
4
x
⫹
5
x ⫺ 3
1 ⫹
3
y ⫺ 6
y ⫹
9
y ⫺ 6
p ⫹
1
p ⫺ 2
1 ⫹
1
p ⫺ 2
8
x
3
⫺
1
27
2
x
⫺
1
3
5
a
⫺
1
4
25
a
2
⫺
1
16
R–63 Section R.5 Rational Expressions and Equations 63
College Algebra Graphs & Models—
WORKING WITH FORMULAS
87. Cost to seize illegal drugs:
The cost C, in millions of
dollars, for a government to find
and seize P% of
a certain illegal drug is modeled
by the rational equation shown.
Complete the table (round to the
nearest dollar) and answer the
following questions.
a. What is the cost of seizing
40% of the drugs? Estimate
the cost at 85%.
b. Why does cost increase
dramatically the closer you get to 100%?
c. Will 100% of the drugs ever be seized?
10 ⱕ P 6 1002
C ⴝ
450P
100 ⴚ P
88. Chemicals in the bloodstream:
Rational equations are often used
to model chemical concentrations
in the bloodstream. The percent
concentration C of a certain drug
H hours after injection into
muscle tissue can be modeled by
the equation shown ( ).
Complete the table (round to the
nearest tenth of a percent) and
answer the following questions.
a. What is the percent
concentration of the drug
3 hr after injection?
b. Why is the concentration virtually equal at
and
c. Why does the concentration begin to decrease?
d. How long will it take for the concentration to
become less than 10%?
H ⫽ 5?H ⫽ 4
H ⱖ 0
C ⴝ
200H
2
H
3
ⴙ 40
H
0
1
2
3
4
5
6
7
200H
2
H
3
ⴙ 40
P
40
60
80
90
93
95
98
100
450P
100 ⴚ P
cob19545_chR_054-064.qxd 7/28/10 2:47 PM Page 63

䊳
APPLICATIONS
89. Stock prices: When a hot new stock hits the market,
its price will often rise dramatically and then taper
off over time. The equation
models the price of stock XYZ d days after it has
“hit the market.” (a) Create a table of values showing
the price of the stock for the first 10 days (rounded to
the nearest dollar) and comment on what you notice.
(b) Find the opening price of the stock. (c) Does the
stock ever return to its original price?
90. Population growth: The Department of Wildlife
introduces 60 elk into a new game reserve. It is
projected that the size of the herd will grow
according to the equation where
N is the number of elk and t is the time in years.
(a) Approximate the population of elk after 14 yr.
(b) If recent counts find 225 elk, approximately
how many years have passed?
91. Typing speed: The number of words per minute
that a beginner can type is approximated by the
equation where N is the number
N ⫽
60t ⫺ 120
t
,
N ⫽
1016 ⫹ 3t2
1 ⫹ 0.05t
,
P ⫽
5017d
2
⫹ 102
d
3
⫹ 50
of words per minute after t weeks,
Use a table to determine how many weeks it takes
for a student to be typing an average of forty-five
words per minute.
92. Memory retention: A group of students is asked
to memorize 50 Russian words that are unfamiliar
to them. The number N of these words that the
average student remembers D days later is modeled
by the equation How many
words are remembered after (a) 1 day? (b) 5 days?
(c) 12 days? (d) 35 days? (e) 100 days? According
to this model, is there a certain number of words
that the average student never forgets?
How many?
93. Pollution removal: For a steel mill, the cost C (in
millions of dollars) to remove toxins from the
resulting sludge is given by where
P is the percent of the toxins removed. What percent
can be removed if the mill spends $88,000,000 on
the cleanup? Round to tenths of a percent.
C ⫽
22P
100 ⫺ P
,
N ⫽
5D ⫹ 35
D
1D ⱖ 12.
3 6 t 6 12.
䊳
EXTENDING THE CONCEPT
94. One of these expressions is not equal to the others.
Identify which and explain why.
a. b.
c. d.
95. The average of A and B is x. The average of C, D,
and E is y. The average of A, B, C, D, and E is:
a. b.
c. d.
31x ⫹ y2
5
21x ⫹ y2
5
2x ⫹ 3y
5
3x ⫹ 2y
5
20
10
#
n
n
20n
#
1
10n
20
#
n ⫼ 10
#
n
20n
10n
96. Given the rational numbers and what is the
reciprocal of the sum of their reciprocals? Given
that and are any two numbers—what is the
reciprocal of the sum of their reciprocals?
c
d
a
b
3
4
,
2
5
64 CHAPTER R A Review of Basic Concepts and Skills R–64
College Algebra Graphs & Models—
cob19545_chR_054-064.qxd 11/23/10 7:09 PM Page 64
College Algebra Graphs & Models—
Square roots and cube roots come from a much larger family called radical expres-
sions. Expressions containing radicals can be found in virtually every field of mathe-
matical study, and are an invaluable tool for modeling many real-world phenomena.
A. Simplifying Radical Expressions of the Form
In previous coursework, you likely noted that only if This definition
cannot be applied to expressions like , since there is no number b such that
. In other words, the expression represents a real number only if
(for a full review of the real numbers and other sets of numbers, see Appendix I at
www.mhhe.com/coburn). Of particular interest to us now is an inverse operation for a
2
.
In other words, what operation can be applied to a
2
to return a? Consider the following.
EXAMPLE 1
䊳
Evaluating a Radical Expression
Evaluate for the values given:
a. b. c.
Solution
䊳
a. b. c.
Now try Exercises 7 and 8
䊳
The pattern seemed to indicate that and that our search for an inverse
operation was complete—until Example 1(c), where we found that
Using the absolute value concept, we can “repair” this apparent discrepancy and state a
general rule for simplifying these expressions: For expressions like
and the radicands can be rewritten as perfect squares and simplified in the same
manner: and
The Square Root of
For any real number a,
EXAMPLE 2
䊳
Simplifying Square Root Expressions
Simplify each expression.
a. b.
Solution
䊳
a.
since
x
could be negative
b.
since
x
5 could be negative
Now try Exercises 9 and 10
䊳
⫽
冟
x ⫺ 5
冟
2x
2
⫺ 10x ⫹ 25 ⫽ 21x ⫺ 52
2
⫽ 13
冟
x
冟
2169x
2
⫽
冟
13x
冟
2x
2
⫺ 10x ⫹ 252169x
2
2a
2
円 a円.
a
2
: 2a
2
2y
6
⫽ 21y
3
2
2
⫽
冟
y
3
冟
.249x
2
⫽ 217x2
2
⫽ 7
冟
x
冟
2y
6
,
249x
2
2a
2
⫽
冟
a
冟
.
21⫺62
2
⫽⫺6.
2a
2
⫽ a
⫽ 6 ⫽ 5 ⫽ 3
21⫺62
2
⫽ 136 25
2
⫽ 125 23
2
⫽ 19
a ⫽⫺6a ⫽ 5a ⫽ 3
2a
2
a ⱖ 01ab
2
⫽⫺16
1⫺16
b
2
⫽ a.1a ⫽ b
1
nn
a
n
R.6 Radicals, Rational Exponents, and Radical Equations
LEARNING OBJECTIVES
In Section R.6 you will review how to:
A. Simplify radical
expressions of the form
B. Rewrite and simplify
radical expressions using
rational exponents
C. Use properties of radicals
to simplify radical
expressions
D. Add and subtract radical
expressions
E. Multiply and divide
radical expressions; write
a radical expression in
simplest form
F. Solve equations and use
formulas involving
radicals
1
n
a
n
R–65 65
cob19545_chR_065-080.qxd 11/22/10 11:15 AM Page 65
To investigate expressions like note the radicand in both and can
be written as a perfect cube. From our earlier definition of cube roots we know
and that every real number has only
one real cube root. For this reason, absolute value notation is not used or needed when
taking cube roots.
The Cube Root of
For any real number a,
EXAMPLE 3
䊳
Simplifying Cube Root Expressions
Simplify each expression.
a. b.
Solution
䊳
a. b.
Now try Exercises 11 and 12
䊳
We can extend these ideas to fourth roots, fifth roots, and so on. For example, the
fifth root of a is b only if In symbols, implies Since an odd
number of negative factors is always negative: and an even number of
negative factors is always positive: we must take the index into account
when evaluating expressions like If n is even and the radicand is unknown,
absolute value notation must be used.
The nth Root of a
n
:
For any real number a,
1. when n is even. 2. when n is odd.
EXAMPLE 4
䊳
Simplifying Radical Expressions
Simplify each expression.
a. b. c. d.
e. f. g. h.
Solution
䊳
a. b. is not a real number
c. d.
e. f.
g. h.
Now try Exercises 13 and 14
䊳
2
7
1x ⫺ 22
7
⫽ x ⫺ 22
6
1m ⫹ 52
6
⫽
冟
m ⫹ 5
冟
⫽ 2p ⫽
冟
2m
冟
or 2
冟
m
冟
2
5
32p
5
⫽ 2
5
12p2
5
2
4
16m
4
⫽ 2
4
12m2
4
1
5
⫺32 ⫽⫺21
5
32 ⫽ 2
1
4
⫺811
4
81 ⫽ 3
2
7
1x ⫺ 22
7
2
6
1m ⫹ 52
6
2
5
32p
5
2
4
16m
4
1
5
⫺321
5
321
4
⫺811
4
81
1
n
a
n
⫽ a1
n
a
n
⫽
冟
a
冟
2
n
a
n
1
n
a
n
.
1⫺22
4
⫽ 16,
1⫺22
5
⫽⫺32,
b
5
⫽ a.1
5
a ⫽ bb
5
⫽ a.
⫽⫺4n
2
⫽⫺3x
2
3
⫺64n
6
⫽ 2
3
1⫺4n
2
2
3
2
3
⫺27x
3
⫽ 2
3
1⫺3x2
3
2
3
⫺64n
6
2
3
⫺27x
3
2
3
a
3
a.
a
3
: 2
3
a
3
1
3
8 ⫽ 2
3
122
3
⫽ 2, 1
3
⫺64 ⫽ 2
3
1⫺42
3
⫽⫺4,
1
3
⫺641
3
82
3
x
3
,
66 CHAPTER R A Review of Basic Concepts and Skills R–66
College Algebra Graphs & Models—
CAUTION
䊳
In Section R.2, we noted that indicating that you cannot square
the individual terms in a sum (the square of a binomial results in a perfect square
trinomial). In a similar way, and you cannot take the square root
of individual terms. There is a big difference between the expressions and
Try evaluating each when and B ⫽ 4.A ⫽ 321A ⫹ B2
2
⫽
冟
A ⫹ B
冟
.
2A
2
⫹ B
2
2A
2
⫹ B
2
⫽ A ⫹ B,
1A ⫹ B2
2
⫽ A
2
⫹ B
2
,
WORTHY OF NOTE
Just as is not a real number,
and do not represent
real numbers. An even number of
repeated factors is always positive!
1
6
⫺161
4
⫺16
1
2
⫺16
A. You’ve just seen how
we can simplify radical
expressions of the form 1
n
a
n
cob19545_chR_065-080.qxd 11/22/10 11:15 AM Page 66
B. Radical Expressions and Rational Exponents
As an alternative to radical notation, a rational (fractional) exponent can be used,
along with the power property of exponents. For notice that an exponent
of one-third can replace the cube root notation and produce the same result:
In the same way, an exponent of one-half can replace the
square root notation: In general, we have the following:
Rational Exponents
If a is a real number and n is an integer greater than 1,
then
provided represents a real number.
EXAMPLE 5
䊳
Simplifying Radical Expressions Using Rational Exponents
Simplify by rewriting each radicand as a perfect nth power and converting to
rational exponent notation.
a. b. c. d.
Solution
䊳
a. b.
c. d.
is not a real number
Now try Exercises 15 and 16
䊳
When a rational exponent is used, as in the
denominator of the exponent represents the index number, while the
numerator of the exponent represents the original power on a. This
is true even when the exponent on a is something other than one! In
other words, the radical expression can be rewritten as
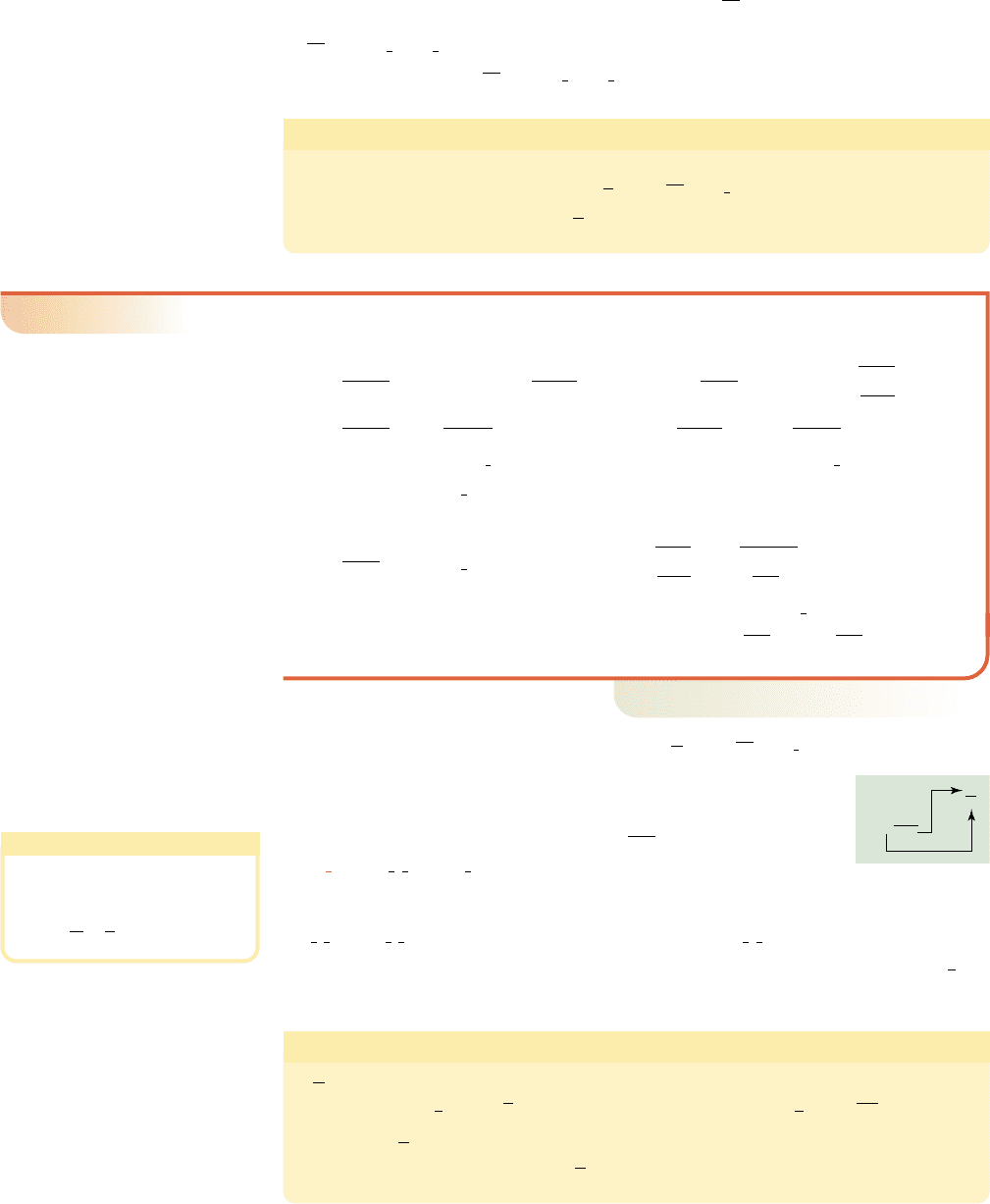
or This is further illustrated in Figure R.6
where we see the rational exponent has the form, “power over root.” To evaluate this
expression without the aid of a calculator, we use the commutative property to rewrite
as and begin with the fourth root of 16:
In general, if m and n have no common factors (other than 1) the expression can
be interpreted in the following two ways.
Rational Exponents
If is a rational number expressed in lowest terms with then
(compute then take the mth power), (compute then take the nth root),
provided represents a real number.1
n
a
a
m
,1
n
a,
112 a
m
n
⫽ 12
n
a2
m
or
122 a
m
n
⫽ 2
n
a
m
n ⱖ 2,
m
n
a
m
n
116
1
4
2
3
1
⫽ 2
3
⫽ 8.116
1
4
2
3
1
116
3
1
2
1
4
16
3
4
.116
3
2
1
4
⫽ 116
3
1
2
1
4
2
4
16
3
1
n
a ⫽ 2
n
a
1
⫽ a
1
n
,
⫽
2w
3
⫽ ca
2w
3
b
3
d
1
3
B
3
8w
3
27
⫽
B
3
a
2w
3
b
3
2
4
⫺81 ⫽ 1⫺812
1
4
⫽⫺2
冟
x
冟
5
⫽⫺5
⫽⫺02x
5
0 ⫽ 1⫺52
3
3
⫽⫺312x
5
2
4
4
1
4
⫽ 31⫺52
3
4
1
3
⫺2
4
16x
20
⫽⫺2
4
12x
5
2
4
2
3
⫺125 ⫽ 2
3
1⫺52
3
B
3
8w
3
27
2
4
⫺81⫺2
4
16x
20
2
3
⫺125
1
n
a
1
n
a ⫽ 2
n
a
1
⫽ a
1
n
2a
2
⫽ 1a
2
2
1
2
⫽ a
2
2
⫽
冟
a
冟
.
2
3
a
3
⫽ 1a
3
2
1
3
⫽ a
3
3
⫽ a.
1
3
a
3
⫽ a,
R–67 Section R.6 Radicals, Rational Exponents, and Radical Equations 67
College Algebra Graphs & Models—
WORTHY OF NOTE
Any rational number can be
decomposed into the product
of a unit fraction and an
integer: .
m
n
⫽
1
n
#
m
(兹a
m
)
n
a
m
n
Figure R.6
cob19545_chR_065-080.qxd 11/22/10 11:15 AM Page 67
One application of the product property is to simplify radical expressions. In gen-
eral, the expression is in simplified form if a has no factors (other than 1) that are
perfect nth roots.
EXAMPLE 7
䊳
Simplifying Radical Expressions
Write each expression in simplest form using the product property.
a. b. c. d.
Solution
䊳
a. b.
⫽ 25x1
3
x
⫽ 5
#
5
#
x
#
1
3
x ⫽ 312
⫽ 5
#
2
3
125
#
2
3
x
3
#
2
3
x
1
⫽ 1912
5 2
3
125x
4
⫽ 5
#
2
3
125
#
x
4
118 ⫽ 19
#
2
2
3
4n
5
1.22
3
16n
4
⫺4 ⫹ 220
2
52
3
125x
4
118
1
n
a
Expressions with rational exponents are generally easier to evaluate if we compute
the root first, then apply the exponent. Computing the root first also helps us determine
whether or not an expression represents a real number.
EXAMPLE 6
䊳
Simplifying Expressions with Rational Exponents
Simplify each expression, if possible.
a. b. c. d.
Solution
䊳
a. b.
or not a real number
c. d.
or
Now try Exercises 17 through 22
䊳
C. Using Properties of Radicals to Simplify Radical Expressions
The properties used to simplify radical expressions are closely connected to the prop-
erties of exponents. For instance, the product to a power property holds even when n
is a rational number. This means and When the second
statement is expressed in radical form, we have with both
forms having a value of 10. This suggests the product property of radicals, which
can be extended to include cube roots, fourth roots, and so on.
Product Property of Radicals
If and represent real-valued expressions, then
and 1
n
A
#
1
n
B ⫽ 1
n
AB.1
n
AB ⫽ 1
n
A
#
1
n
B
1
n
B1
n
A
14
#
25 ⫽ 14
#
225,
14
#
252
1
2
⫽ 4
1
2
#
25
1
2
.1xy2
1
2
⫽ x
1
2
y
1
2
⫺
1
4
⫽⫺2
⫺2
⫽ 1⫺22
2
or 4
⫽⫺11
3
82
⫺2
⫽ 11
3
⫺82
2
⫺8
⫺
2
3
⫽⫺18
1
3
2
⫺2
1⫺82
2
3
⫽
3
1⫺82
1
3
4
2
⫺343 ⫽⫺172
3
⫽ 11⫺492
3
⫽⫺11492
3
1⫺492
3
2
⫽ 31⫺492
1
2
4
3
, ⫺49
3
2
⫽⫺149
1
2
2
3
⫺8
⫺
2
3
1⫺82
2
3
1⫺492
3
2
⫺49
3
2
68 CHAPTER R A Review of Basic Concepts and Skills R–68
College Algebra Graphs & Models—
WORTHY OF NOTE
While the expression
represents the real number the
expression is not a
real number, even though
Note that the second exponent is
not in lowest terms.
1
3
⫽
2
6
.
1⫺82
2
6
⫽ 11
6
⫺82
2
⫺2,
1⫺82
1
3
⫽ 1
3
⫺8
B. You’ve just seen how
we can rewrite and simplify
radical expressions using
rational exponents
CAUTION
䊳
Note that this property applies only to a product of two terms, not to a sum or difference.
In other words, while 29 ⫹ x
2
⫽
|
3 ⫹ x
|
!29x
2
⫽
冟
3x
冟
,
e
These steps can
be done mentally
cob19545_chR_065-080.qxd 7/28/10 2:14 PM Page 68
c. d.
Now try Exercises 23 through 26
䊳
When radicals are combined using the product property, the result may contain a
perfect nth root, which should be simplified. Note that the index numbers must be the
same in order to use this property.
⫽⫺2 ⫹ 15
⫽
1
21⫺2 ⫹ 152
2
⫽
⫺4 ⫹ 215
2
1.22
3
16n
4
2
3
4n
5
⫽ 1.22
3
64
#
n
9
⫺4 ⫹ 120
2
⫽
⫺4 ⫹ 14
#
5
2
R–69 Section R.6 Radicals, Rational Exponents, and Radical Equations 69
College Algebra Graphs & Models—
WORTHY OF NOTE
For expressions like those in
Example 7(c), students must
resist the “temptation” to reduce
individual terms as in
Remember, only factors can
be reduced.
⫺4 ⫹ 120
2
⫽⫺2 ⫹ 120.
⫽ 4.8n
3
⫽ 1.2142n
3
⫽ 1.22
3
642
3
1n
3
2
3
⫽ 1.22
3
642
3
n
9
Quotient Property of Radicals
If and represent real-valued expressions with then
and .
Many times the product and quotient properties must work together to simplify a
radical expression, as shown in Example 8A.
EXAMPLE 8A
䊳
Simplifying Radical Expressions
Simplify each expression:
a. b.
Solution
䊳
a. b.
Radical expressions can also be simplified using rational exponents.
EXAMPLE 8B
䊳
Using Rational Exponents to Simplify Radical Expressions
Simplify using rational exponents:
a. b. c.
Solution
䊳
a. b. c.
Now try Exercises 27 through 30
䊳
⫽ v
2
1
3
v ⫽ 6p
2
q
2
1q
⫽ 2
6
m
5
⫽ v
6
3
v
1
3
⫽ 6p
2
q
2
q
1
2
⫽ m
5
6
⫽ v
7
3
⫽ 6p
2
q
1
4
2
⫹
1
2
2
⫽ m
1
3
⫹
1
2
⫽ v
3
3
#
v
4
3
⫽ 36
1
2
p
4
2
q
5
2
1
3
m1m ⫽ m
1
3
m
1
2
v2
3
v
4
⫽ v
1
#
v
4
3
236p
4
q
5
⫽ 136p
4
q
5
2
1
2
1
3
m1mv2
3
v
4
236p
4
q
5
⫽
31
3
3
5x
⫽ 3a
2
⫽
1
3
27
#
3
5x
⫽ 29a
4
A
3
81
125x
3
⫽
1
3
81
2
3
125x
3
218a
5
22a
⫽
B
18a
5
2a
A
3
81
125x
3
218a
5
22a
1
n
A
1
n
B
⫽
A
n
A
BA
n
A
B
⫽
1
n
A
1
n
B
B ⫽ 0,1
n
B1
n
A
C. You’ve just seen how
we can use properties of
radicals to simplify radical
expressions
The quotient property of radicals can also be established using exponential
properties. The fact that suggests the following:
1100
125
⫽
A
100
25
⫽ 2
cob19545_chR_065-080.qxd 11/22/10 11:15 AM Page 69
