Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models
Подождите немного. Документ загружается.

80 CHAPTER R A Review of Basic Concepts and Skills R–80
College Algebra Graphs & Models—
millions of miles (Kepler’s third law of planetary
motion). Use the equation to approximate the
maximum radius of each orbit, given the number of
days it takes for one revolution. (See Exercises 65
and 66.)
a. Mercury: 88 days
b. Venus: 225 days
c. Earth: 365 days
d. Mars: 687 days
e. Jupiter: 4333 days
f. Saturn: 10,759 days
72. Wind-powered energy: If a wind-powered
generator is delivering P units of power, the
velocity V of the wind (in miles per hour) can be
determined using where k is a constant
that depends on the size and efficiency of the
generator. Given approximately how
many units of power are being delivered if the
wind is blowing at 27 miles per hour? (See
Exercise 68.)
k ⫽ 0.004,
V ⫽
A
3
P
k
,
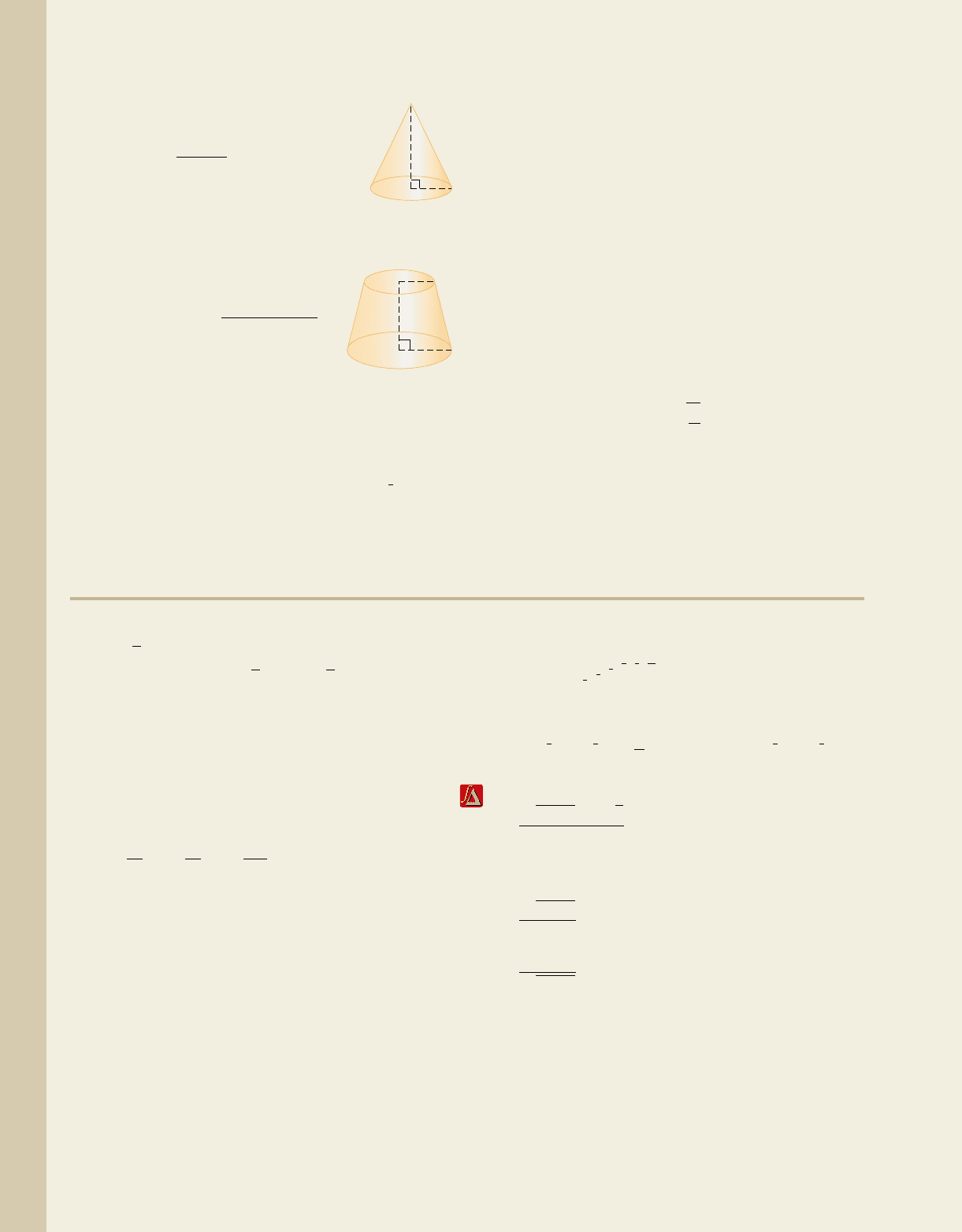
69. Surface area: The lateral surface
area (surface area excluding the base)
S of a cone is given by the formula
where r is the
radius of the base and h is the height
of the cone. Find the lateral surface
area of a cone that has a radius of 6 m and a height of
10 m. Answer in simplest form.
70. Surface area: The lateral surface
area S of a frustum (a truncated
cone) is given by the formula
where a is the radius of the upper
base, b is the radius of the lower
base, and h is the height. Find the surface area of a
frustum where and
Answer in simplest form.
71. Planetary motion: The time T (in days) for a
planet to make one revolution (elliptical orbit)
around the sun is modeled by where
R is the maximum radius of the planet’s orbit in
T ⫽ 0.407R
3
2
,
h ⫽ 10 m.b ⫽ 8 m,a ⫽ 6 m,
S ⫽ 1a ⫹ b22h
2
⫹ 1b ⫺ a2
2
,
S ⫽ r2r
2
⫹ h
2
,
h
r
h
a
b
䊳
EXTENDING THE CONCEPT
The expression is not factorable using integer
values. But the expression can be written in the form
enabling us to factor it as a “binomial”
and its conjugate: Use this idea to
factor the following expressions.
73. a.
b.
74. a.
b.
75. The following terms form a pattern that continues
until the sixth term is found:
(a) Compute the sum
of all six terms; (b) develop a system (investigate
the pattern further) that will enable you to find the
sum of 12 such terms without actually writing out
the terms.
23x
⫹ 29x ⫹ 227x ⫹ p
9w
2
⫺ 17
4v
2
⫺ 11
n
2
⫺ 19
x
2
⫺ 5
1x 27
2 1x 272.
x
2
1272
2
,
x
2
7
76. Find a quick way to simplify the expression
without the aid of a calculator.
77. If find the value of
78. Rewrite by rationalizing the numerator:
Determine the values of x for which each expression
represents a real number.
79.
80.
x
2
⫺ 4
1x ⫺ 1
1x ⫺ 1
x
2
⫺ 4
1x ⫹ h
⫺ 1x
h
x
1
2
⫹ x
⫺
1
2
.1x
1
2
⫹ x
⫺
1
2
2
2
⫽
9
2
,
a3
5
6
b
3
2
4
5
3
4
2
5
10
3
aaa
a
aaa
a
cob19545_chR_065-080.qxd 7/28/10 2:16 PM Page 80

R–81 Overview of Chapter R 81
College Algebra Graphs & Models—
Prerequisite Definitions, Properties, Formulas, and Relationships
Notation and Relations
concept notation description example
•
Set notation: {members} braces enclose the members of a set set of even whole numbers
•
Is an element of indicates membership in a set
•
Empty set or { } a set having no elements odd numbers in A
•
Is a proper subset of indicates the elements of one set
are entirely contained in another
•
Defining a set the set of all x, such that x ...
Sets of Numbers
•
Natural:
•
Whole:
•
Integers:
•
Rational:
•
Irrational: {numbers with a nonterminating,
•
{all rational and irrational numbers}
nonrepeating decimal form}
Absolute Value of a Number Distance between numbers a and b
on the number line
•
The distance between a number n
and zero (always positive) or
For a complete review of these ideas, go to www.mhhe.com/coburn.
R.1 Properties of Real Numbers: For real numbers a, b, and c,
Commutative Property Associative Property
•
Addition:
•
Addition:
•
Multiplication:
•
Multiplication:
Identities Inverses
•
Additive:
•
Additive:
•
Multiplicative:
•
Multiplicative:
R.2 Properties of Exponents: For real numbers a and b, and integers m, n, and p
(excluding 0 raised to a nonpositive power),
•
Product property:
•
Product to a power:
•
Quotient property:
•
Negative exponents:
1a, b ⫽ 02
b
⫺n
⫽
1
b
n
; a
a
b
b
⫺n
⫽ a
b
a
b
n
b
m
b
n
⫽ b
m⫺n
1b ⫽ 02
1a
m
b
n
2
p
⫽ a
mp
#
b
np
b
m
#
b
n
⫽ b
m⫹n
p
q
#
q
p
⫽ 1; p, q ⫽ 01
#
a ⫽ a
a ⫹ 1⫺a2⫽ 00 ⫹ a ⫽ a
1a
#
b2
#
c ⫽ a
#
1b
#
c2a
#
b ⫽ b
#
a
1a ⫹ b2⫹ c ⫽ a ⫹ 1b ⫹ c2a ⫹ b ⫽ b ⫹ a
0n0⫽ e
n if n ⱖ 0
⫺n if n 6 0
冟
b ⫺ a
冟冟
a ⫺ b
冟
Real: ⺢ ⫽⺘ ⫽
⺡ ⫽ e
p
q
, where p, q 僆 ⺪; q ⫽ 0f⺪ ⫽ 5p , ⫺3, ⫺2, ⫺1, 0, 1, 2, 3, p6
⺧ ⫽ 50, 1, 2, 3, p6⺞ ⫽ 51, 2, 3, 4, p6
S ⫽ 5x
|
x ⫽ 6n for n 僆 ⺧65x
|
x p6
S ( A
S ⫽ 50, 6, 12, 18, 24, p6(
⭋
14 僆 A僆
A ⫽ 50, 2, 4, 6, 8, p6
•
Power property:
•
Quotient to a power:
•
Zero exponents:
•
Scientific notation: N ⫻ 10
k
; 1 ⱕ
冟
N
冟
6 10, k 僆 ⺪
b
0
⫽ 1 1b ⫽ 02
a
a
m
b
n
b
p
⫽
a
mp
b
np
1b ⫽ 02
1b
m
2
n
⫽ b
mn
OVERVIEW OF CHAPTER R
cob19545_chR_081-084.qxd 7/28/10 4:48 PM Page 81

82 CHAPTER R A Review of Basic Concepts and Skills R–82
College Algebra Graphs & Models—
R.2 Polynomials
•
A polynomial is a sum or difference of monomial terms
•
Polynomials are classified as a monomial, binomial, trinomial, or polynomial, depending on the number of terms
•
The degree of a polynomial in one variable is the same as the largest exponent occuring on the variable in any term
•
A polynomial expression is in standard form when written with the terms in descending order of degree
R.3 Solving Linear Equations and Inequalities
•
Properties of Equality:
additive property multiplicative property
If A and B are algebraic expressions, where , If A and B are algebraic expressions, where ,
then . then
[C can be positive or negative] and
•
A linear equation in one variable is one that can be written in the form , where the exponent on the
variable is a 1.
•
To solve a linear equation, we attempt to isolate the term containing the variable using the additive property, then
solve for the variable using the multiplicative property.
•
An equation can be an identity (always true), a contradiction (never true) or conditional (true or false depending
on the input value[s]).
•
If an equation contains fractions, multiplying both sides by the least common denominator of all fractions will
“clear the denominators” and reduce the amount of work required to solve.
•
Inequalities are solved using properties similar to those used for solving equations. The one exception is when
multiplying or dividing by a negative quantity, as the inequality symbol must then be reversed to maintain the
truth of the resulting statement.
•
Solutions to an inequality can be given using a simple inequality, graphed on a number line, stated in set notation,
or stated using interval notation.
•
Given two sets A and B: A intersect B is the set of elements shared by both A and B (elements common to
both sets). A union B is the set of elements in either A or B (elements are combined to form a larger set).
•
Compound inequalities are formed using the conjunction “and” or the conjunction “or.” The result can be either a
joint inequality as in , or a disjoint inequality, or .
R.4 Special Factorizations
••
••
•
Certain equations of higher degree can be solved using factoring skills and the zero product property.
R.5 Rational Expressions: For polynomials P, Q, R, and S with no denominator of zero,
•
Lowest terms:
•
Equivalence:
•
Multiplication:
•
Division:
•
Addition:
•
Subtraction:
•
Addition/subtraction with unlike denominators:
1. Find the LCD of all rational expressions.
2. Build equivalent expressions using LCD.
3. Add/subtract numerators as indicated.
4. Write the result in lowest terms.
•
To solve rational equations, first clear denominators using the LCD, noting values that must be excluded.
•
Multiplying an equation by a variable quantity sometimes introduces extraneous solutions. Check all results in the
original equation.
P
R
⫺
Q
R
⫽
P ⫺ Q
R
P
R
⫹
Q
R
⫽
P ⫹ Q
R
P
Q
⫼
R
S
⫽
P
Q
#
S
R
⫽
PS
QR
P
Q
#
R
S
⫽
P
#
R
Q
#
S
⫽
PR
QS
P
Q
⫽
P
#
R
Q
#
R
P
#
R
Q
#
R
⫽
P
Q
A
3
⫹ B
3
⫽ 1A ⫹ B21A
2
⫺ AB ⫹ B
2
2A
3
⫺ B
3
⫽ 1A ⫺ B21A
2
⫹ AB ⫹ B
2
2
A
2
⫾ 2AB ⫹ B
2
⫽ 1A ⫾ B2
2
A
2
⫺ B
2
⫽ 1A ⫹ B21A ⫺ B2
x 7 7x 6 ⫺2⫺3 6 x ⱕ 5
1A ´ B2
1A ¨ B2
ax ⫹ b ⫽ c
A
C
⫽
B
C
;C ⫽ 0
A
#
C ⫽ B
#
CA ⫹ C ⫽ B ⫹ C
A ⫽ BA ⫽ B
cob19545_chR_081-084.qxd 7/28/10 4:48 PM Page 82

R–83 Practice Test 83
College Algebra Graphs & Models—
R.6 Properties of Radicals
•
is a real number only for
•
only if
•
For any real number a, when n is even
•
If a is a real number and n is an integer greater
than 1, then provided represents a
real number
•
If and represent real numbers,
•
A radical expression is in simplest form when: 1. the radicand has no factors that are perfect nth roots,
2. the radicand contains no fractions, and
3. no radicals occur in a denominator.
1
n
AB ⫽ 1
n
A
#
1
n
B
1
n
B1
n
A
1
n
a 1
n
a ⫽ a
1
n
1
n
a
n
⫽
冟
a
冟
b
n
⫽ a1
n
a ⫽ b,
a ⱖ 01a
•
only if
•
If n is even, represents a real number only
if
•
For any real number a, when n is odd
•
If is a rational number written in lowest terms
with , then and
provided represents a real number.
•
If and represent real numbers and
B
n
A
B
⫽
1
n
A
1
n
B
B ⫽ 0,1
n
B1
n
A
2
n
a
a
m
n
⫽ 1
n
a
m
a
m
n
⫽ 11
n
a2
m
n ⱖ 2
m
n
1
n
a
n
⫽ a
a ⱖ 0
1
n
a
b
2
⫽ a1a ⫽ b,
R.6 Pythagorean Theorem
•
For any right triangle with legs a and b and
hypotenuse c: .a
2
⫹ b
2
⫽ c
2
•
For any triangle with sides a, b,and c,if
then the triangle is a right triangle.a
2
⫹ b
2
⫽ c
2
,
•
To solve radical equations, isolate the radical on one side, then apply the appropriate “nth power” to free up the
radicand. Repeat the process if needed. See flowchart on page 74.
•
For equations with a rational exponent isolate the variable term and raise both sides to the power. If m is even,
there will be two real solutions.
n
m
m
n
,
1. State true or false. If false, state why.
a. b.
c. d.
2. State the value of each expression.
a. b.
c. d.
3. Evaluate each expression:
a. b.
c. d.
4. Evaluate each expression:
a. b.
c. d.
5. Evaluate using a calculator:
6. State the value of each expression, if possible.
a. b. 6 ⫼ 00 ⫼ 6
2000
a1 ⫹
0.08
12
b
12
#
10
4.2 ⫼ 1⫺0.62
⫺2.8
⫺0.7
1⫺0.621⫺1.521⫺42a⫺2
1
3
b
1.3 ⫹ 1⫺5.92⫺0.7 ⫹ 1.2
⫺
1
3
⫺
5
6
7
8
⫺ a⫺
1
4
b
1400
1⫺36
1
3
⫺1251 121
⫺21x ⫺ 32⫽⫺2x ⫺ 3x ⫺ 3 ⫽⫺3 ⫹ x
7
0
⫽ 013 ⫹ 42
2
⫽ 25
7. State the number of terms in each expression and
identify the coefficient of each.
a. b.
8. Evaluate each expression given and
. Round to hundredths as needed.
a. b.
9. Translate each phrase into an algebraic expression.
a. Nine less than twice a number is subtracted from
the number cubed.
b. Three times the square of half a number is
subtracted from twice the number.
10. Create a mathematical model using descriptive
variables.
a. The radius of the planet Jupiter is approximately
119 mi less than 11 times the radius of the Earth.
Express the radius of Jupiter in terms of the
Earth’s radius.
b. Last year, Video Venue Inc. earned $1.2 million
more than four times what it earned this year.
Express last year’s earnings of Video Venue Inc.
in terms of this year’s earnings.
12
⫺ x14 ⫺ x
2
2⫹
y
x
2x ⫺ 3y
2
y ⫽⫺2
x ⫽⫺0.5
c ⫹ 2
3
⫹ c⫺2v
2
⫹ 6v ⫹ 5
PRACTICE TEST
cob19545_chR_081-084.qxd 7/28/10 4:48 PM Page 83

84 CHAPTER R A Review of Basic Concepts and Skills R–84
College Algebra Graphs & Models—
11. Simplify by combining like terms.
a.
b.
c.
12. Factor each expression completely.
a. b.
c.
13. Simplify using the properties of exponents.
a. b.
c. d.
14. Simplify using the properties of exponents.
a.
b.
c. d.
15. Compute each product.
a.
b.
16. Add or subtract as indicated.
a.
b.
Simplify or compute as indicated.
17. a. b.
c. d.
e.
f.
18. a. b.
c. d.
e. f.
g. h.
8
16 ⫺ 12
B
2
5x
1x ⫹ 1521x ⫺ 1527140 ⫺ 190
⫺4 ⫹ 132
8
a
25
16
b
⫺3
2
A
3
⫺8
27v
3
21x ⫹ 112
2
m ⫹ 3
m
2
⫹ m ⫺ 12
⫺
2
51m ⫹ 42
x
2
⫺ 25
3x
2
⫺ 11x ⫺ 4
⫼
x
2
⫹ x ⫺ 20
x
2
⫺ 8x ⫹ 16
3x
2
⫺ 13x ⫺ 10
9x
2
⫺ 4
x
3
⫺ 27
x
2
⫹ 3x ⫹ 9
4 ⫺ n
2
n
2
⫺ 4n ⫹ 4
x ⫺ 5
5 ⫺ x
12x
2
⫹ 4x ⫺ 92⫺ 17x
4
⫺ 2x
2
⫺ x ⫺ 92
1⫺5a
3
⫹ 4a
2
⫺ 32⫹ 17a
4
⫹ 4a
2
⫺ 3a ⫺ 152
12a ⫹ 3b2
2
13x
2
⫹ 5y213x
2
⫺ 5y2
⫺7x
0
⫹ 1⫺7x2
0
a
a
⫺3
#
b
c
⫺2
b
⫺4
13.2 ⫻ 10
⫺17
2⫻ 12.0 ⫻ 10
15
2
⫺12a
3
b
5
3a
2
b
4
a
5p
2
q
3
r
4
⫺2pq
2
r
4
b
2
a
m
2
2n
b
3
1⫺2a
3
2
2
1a
2
b
4
2
3
5
b
⫺3
x
3
⫹ 5x
2
⫺ 9x ⫺ 45
4v
3
⫺ 12v
2
⫹ 9v9x
2
⫺ 16
4x ⫺ 1x ⫺ 2x
2
2⫹ x13 ⫺ x2
⫺413b ⫺ 22⫹ 5b
8v
2
⫹ 4v ⫺ 7 ⫹ v
2
⫺ v
19. Maximizing revenue: Due to past experience, the
manager of a video store knows that if a popular
video game is priced at $30, the store will sell 40
each day. For each decrease of $0.50, one additional
sale will be made. The formula for the store’s
revenue is then where x
represents the number of times the price is
decreased. Multiply the binomials and use a table of
values to determine (a) the number of decreases
that will give the most revenue and (b) the maximum
amount of revenue.
20. Diagonal of a rectangular
prism: Use the Pythagorean
theorem to determine the
length of the diagonal of the
rectangular prism shown in
the figure. (Hint: First find
the diagonal of the base.)
21. Solve each linear equation.
a. b.
c. d.
e.
f.
22. If one-fourth of the sum of a number and twelve is
added to three, the result is sixteen. Find an equation
model for this statement, then use it to find the
number.
23. Solve each polynomial equation by factoring.
a.
b.
c.
24. Solve each rational equation.
a.
b.
c.
25. Solve each radical equation.
a.
b.
c. 13x ⫹ 4
⫽ 2 ⫺ 1x ⫹ 2
31x ⫹ 4 ⫽ x ⫹ 4
2x
2
⫹ 7
2
⫹ 3 ⫽ 5
n
n ⫹ 2
⫺
3
n ⫺ 4
⫽
4n ⫹ 20
n
2
⫺ 2n ⫺ 8
3h
h ⫹ 3
⫺
7
h
2
⫹ 3h
⫽
1
h
3
5x
⫹
7
10
⫽
1
4x
g
4
⫺ 10g
2
⫹ 9 ⫽ 0
⫺7r
3
⫹ 21r
2
⫹ 28r ⫽ 0
x
3
⫺ 7x
2
⫽ 4x ⫺ 28
⫺
g
6
⫽ 3 ⫺
1
2
⫺
5g
12
⫺813p ⫹ 52⫺ 9 ⫽ 613 ⫺ 4p2
1
2
x ⫹
2
3
⫽
3
4
4m ⫺ 5 ⫽ 11m ⫹ 2
312n ⫺ 62⫹ 1 ⫽ 7⫺2b ⫹ 7 ⫽⫺5
50¢
R ⫽ 130 ⫺ 0.5x2140 ⫹ x2,
42 cm
32 cm
24 cm
cob19545_chR_081-084.qxd 11/22/10 10:29 AM Page 84

College Algebra G&M—
Relations, Functions,
and Graphs
CHAPTER OUTLINE
1.1 Rectangular Coordinates; Graphing Circles
and Other Relations 86
1.2 Linear Equations and Rates of Change 103
1.3 Functions, Function Notation, and the
Graph of a Function 117
1.4 Linear Functions, Special Forms, and
More on Rates of Change 134
1.5 Solving Equations and Inequalities Graphically;
Formulas and Problem Solving 148
1.6 Linear Function Models and Real Data 163
CHAPTER CONNECTIONS
Viewing relations and functions in terms of an
equation, a table of values, and the related
graph, often brings a clearer understanding of
the relationships involved. For instance, while
many business are aware that internet use is
increasing with time, they are very interested
in the
rate of growth
, in order to prepare and
develop related goods and services. This
application appears as Exercise 109 in
Section 1.4.
Check out these other real-world connections
䊳
Earthquake Range: Section 1.1, Exercise 96
䊳
Garbage Collection: Section 1.2, Exercise 42
䊳
Eating Out: Section 1.4, Exercise 112
䊳
Credit Card Use: Section 1.6, Exercise 33
85
cob19545_ch01_085-102.qxd 11/22/10 1:08 PM Page 85

1.1 Rectangular Coordinates; Graphing Circles and Other Relations
In everyday life, we encounter a large variety of relationships. For instance, the time it
takes us to get to work is related to our average speed; the monthly cost of heating a
home is related to the average outdoor temperature; and in many cases, the amount of
our charitable giving is related to changes in the cost of living. In each case we say that
a relation exists between the two quantities.
A. Relations, Mapping Notation, and Ordered Pairs
In the most general sense, a relation is simply a corre-
spondence between two sets. Relations can be repre-
sented in many different ways and may even be very
“unmathematical,” like the one shown in Figure 1.1
between a set of people and the set of their correspond-
ing birthdays. If P represents the set of people and B
represents the set of birthdays, we say that elements of
P correspond to elements of B, or the birthday relation
maps elements of Pto elements of B. Using what is called
mapping notation, we might simply write From
a purely practical standpoint, we note that while it is possible for two different people
to share the same birthday, it is quite impossible for the same person to have two different
birthdays. Later, this observation will help us mark the difference between a relation
and special kind of relation called a function.
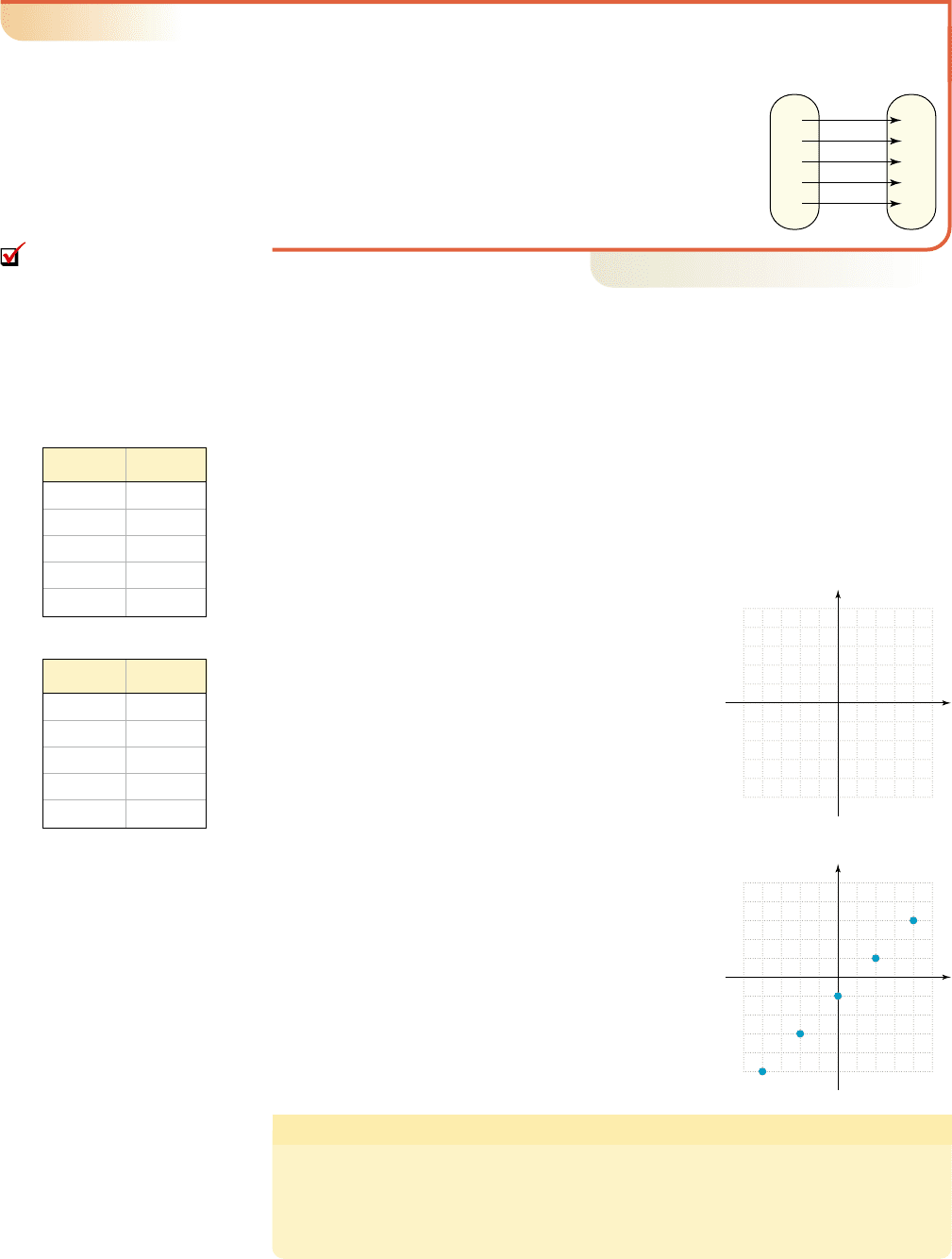
The bar graph in Figure 1.2 is also an
example of a relation. In the graph, each
year is related to annual consumer spend-
ing per person on cable and satellite televi-
sion. As an alternative to mapping or a bar
graph, this relation could also be repre-
sented using ordered pairs. For example,
the ordered pair (5, 234) would indicate
that in 2005, spending per person on
cable and satellite TV in the United
States averaged $234. When a relation is
represented using ordered pairs, we say
the relation is pointwise-defined.
Over a long period of time, we could
collect many ordered pairs of the form (t, s), where consumer spending s depends on the
time t. For this reason we often call the second coordinate of an ordered pair (in this case s)
the dependent variable, with the first coordinate designated as the independent variable.
The set of all first coordinates is called the domain of the relation. The set of all second
coordinates is called the range.
P S B.
LEARNING OBJECTIVES
In Section 1.1 you will see
how we can:
A. Express a relation in
mapping notation and
ordered pair form
B. Graph a relation
C. Graph relations on
a calculator
D. Develop the equation and
graph of a circle using
the distance and midpoint
formulas
86 1–2
College Algebra G&M—
Consumer spending
(dollars per year)
400
500
300
200
100
795
($192)
($234)
($281)
($375)
($411-est)
3 11
Year (0 → 2000)
Missy
Jeff
Angie
Megan
Mackenzie
Michael
Mitchell
April 12
Nov 11
Sept 10
Nov 28
May 7
April 14
PB
Figure 1.1
Figure 1.2
Source: 2009 Statistical Abstract of the United States,
Table 1089 (some figures are estimates)
cob19545_ch01_085-102.qxd 11/1/10 8:52 AM Page 86
B. The Graph of a Relation
Relations can also be stated in equation form. The equation expresses a
relation where each y-value is one less than the corresponding x-value (see Table 1.1).
The equation expresses a relation where each x-value corresponds to the
absolute value of y (see Table 1.2). In each case, the relation is the set of all ordered
pairs (x, y) that create a true statement when substituted, and a few ordered pair solu-
tions are shown in the tables for each equation.
Relations can be expressed graphically using a rec-
tangular coordinate system. It consists of a horizontal
number line (the x-axis) and a vertical number line (the
y-axis) intersecting at their zero marks. The point of inter-
section is called the origin. The x- and y-axes create a
flat, two-dimensional surface called the xy-plane and
divide the plane into four regions called quadrants.
These are labeled using a capital “Q” (for quadrant) and
the Roman numerals I through IV, beginning in the
upper right and moving counterclockwise (Figure 1.3).
The grid lines shown denote the integer values on each
axis and further divide the plane into a coordinate grid,
where every point in the plane corresponds to an ordered
pair. Since a point at the origin has not moved along either
axis, it has coordinates (0, 0). To plot a point (x, y) means
we place a dot at its location in the xy-plane. A few of the
ordered pairs from are plotted in Figure 1.4,
where a noticeable pattern emerges—the points seem to
lie along a straight line.
If a relation is pointwise-defined, the graph of the
relation is simply the plotted points. The graph of a re-
lation in equation form, such as , is the set of
all ordered pairs (x, y) that are solutions (make the
equation true).
Solutions to an Equation in Two Variables
1. If substituting and results in a true equation, the ordered pair
(a, b) is a solution and on the graph of the relation.
2. If the ordered pair (a, b) is on the graph of a relation, it is a solution
(substituting and will result in a true equation).y bx a
y bx a
y x 1
y x 1
x
冟
y
冟
y x 1
1–3 Section 1.1 Rectangular Coordinates; Graphing Circles and Other Relations 87
College Algebra G&M—
Table 1.1 y ⴝ x ⴚ 1
Table 1.2 x ⴝ 円y円
EXAMPLE 1
䊳
Expressing a Relation as a Mapping and as a Pointwise-Defined Relation
Represent the relation from Figure 1.2 in mapping notation
and as a pointwise-defined relation, then state its
domain and range.
Solution
䊳
Let t represent the year and s represent consumer spending.
The mapping gives the diagram shown. As a pointwise-
defined relation we have (3, 192), (5, 234), (7, 281), (9, 375),
and (11, 411). The domain is the set {3, 5, 7, 9, 11}; the
range is {192, 234, 281, 375, 411}.
Now try Exercises 7 through 12
䊳
For more on this relation, see Exercise 93.
t S s
ts
192
234
281
375
411
3
5
7
9
11
x
QIQII
QIVQIII
y
543215 4 3 2 1
1
2
3
4
5
2
3
4
5
1
x
y
55
5
5
(2, 3)
(4, 5)
(0, 1)
(4, 3)
(2, 1)
Figure 1.3
Figure 1.4
A. You’ve just seen how
we can express a relation in
mapping notation and ordered
pair form
xy
0
21
43
1
32
54
xy
2
1
00
11
22
1
2
cob19545_ch01_085-102.qxd 11/1/10 8:52 AM Page 87
88 CHAPTER 1 Relations, Functions, and Graphs 1–4
College Algebra G&M—
(4, 3)
(2, 1)
(0, 1)
(2, 3)
(4, 5)
y x 1
x
y
55
5
5
(2, 2)
(0, 0)
(2, 2)
x y
x
y
55
5
5
Figure 1.5
Figure 1.7
y x 1: selected integer values
Figure 1.9
y x 1: selected real number values
Figure 1.10
y x 1: all real number values
Figure 1.8
y x 1: selected rational values
Figure 1.6
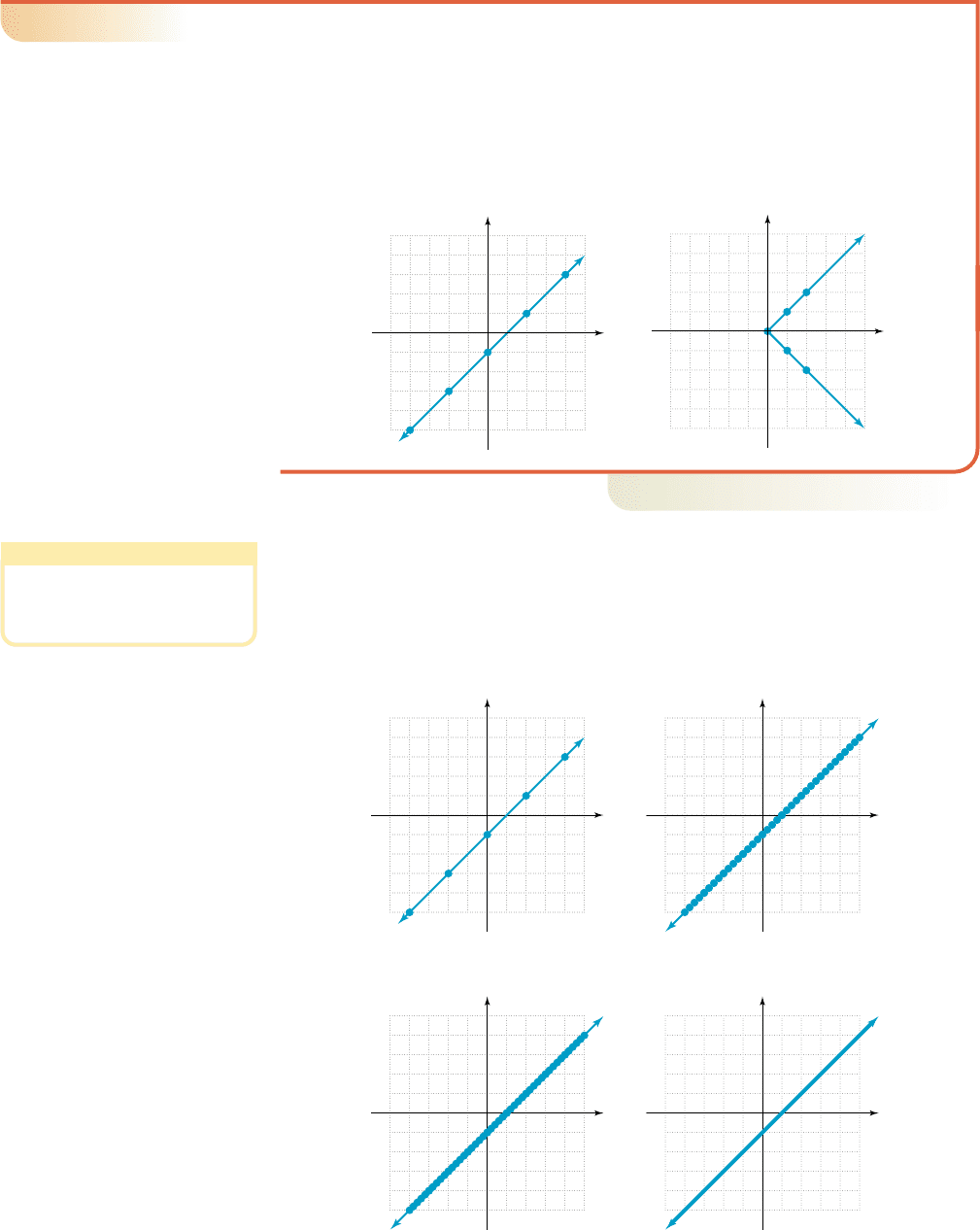
WORTHY OF NOTE
As the graphs in Example 2
indicate, arrowheads are used
where appropriate to indicate the
infinite extension of a graph.
Now try Exercises 13 through 16
䊳
While we used only a few points to graph the relations in Example 2, they are
actually made up of an infinite number of ordered pairs that satisfy each equation, includ-
ing those that might be rational or irrational. This understanding is an important part of
reading and interpreting graphs, and is illustrated for you in Figures 1.7 through 1.10.
x
y
55
5
5
x
y
55
5
5
x
y
55
5
5
x
y
55
5
5
We generally use only a few select points to determine the shape of a graph, then draw a
straight line or smooth curve through these points, as indicated by any patterns formed.
EXAMPLE 2
䊳
Graphing Relations
Graph the relations and using the ordered pairs given in Tables 1.1
and 1.2.
Solution
䊳
For , we plot the points then connect them with a straight line (Figure 1.5).
For , the plotted points form a V-shaped graph made up of two half lines
(Figure 1.6).
x
冟
y
冟
y x 1
x
冟
y
冟
y x 1
cob19545_ch01_085-102.qxd 11/1/10 8:52 AM Page 88
Since there are an infinite number of ordered pairs forming the graph of , the
domain cannot be given in list form. Here we note x can be any real number and write
D: Likewise, y can be any real number and for the range we have R: All
of these points together make these graphs continuous, which for our purposes means
you can draw the entire graph without lifting your pencil from the paper.
Actually, a majority of graphs cannot be drawn using only a straight line or directed
line segments. In these cases, we rely on a “sufficient number” of points to outline the
basic shape of the graph, then connect the points with a smooth curve. As your experi-
ence with graphing increases, this “sufficient number of points” tends to get smaller as
you learn to anticipate what the graph of a given relation should look like. In particular,
for the linear graph in Figure 1.5 we notice that both the x- and y-variables have an
implied exponent of 1. This is in fact a characteristic of linear equations and graphs. In
Example 3 we’ll notice that if the exponent on one of the variables is 2 (either x or y is
squared) while the other exponent is 1, the result is a graph called a parabola. If the
x-term is squared (Example 3a) the parabola is oriented vertically, as in Figure 1.11,
and its highest or lowest point is called the vertex. If the y-term is squared (Example 3c),
the parabola is oriented horizontally, as in Figure 1.13, and the leftmost or rightmost
point is the vertex. The graphs and equations of other relations likewise have certain
identifying characteristics. See Exercises 85 through 92.
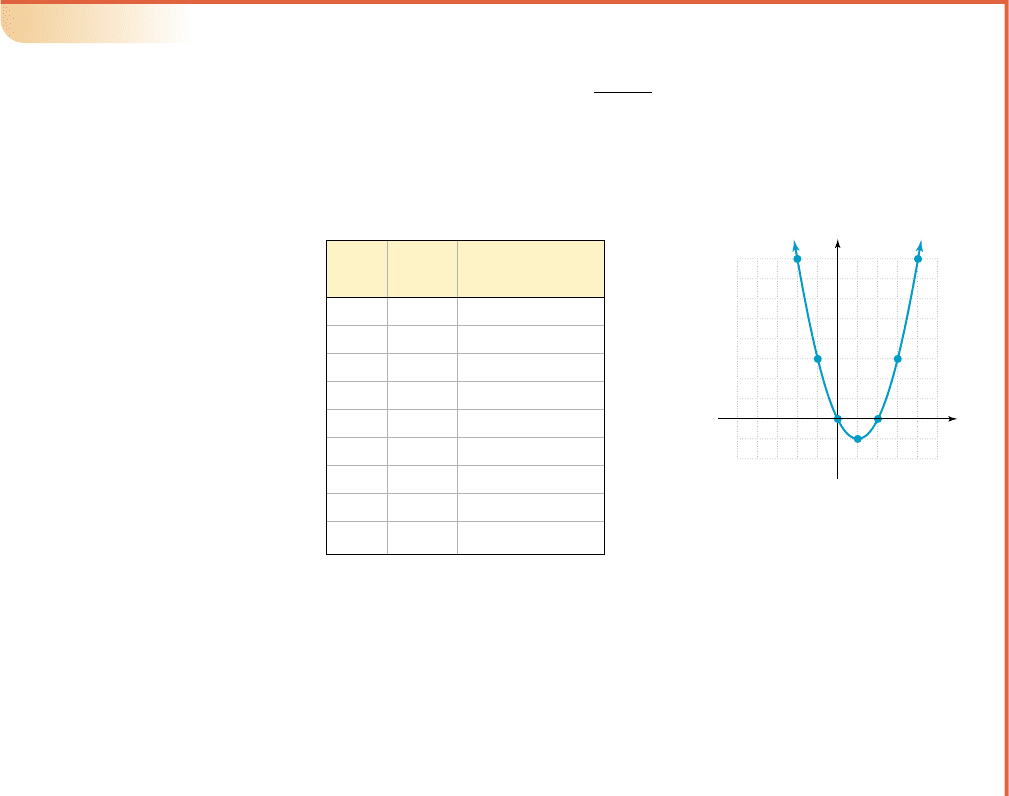
EXAMPLE 3
䊳
Graphing Relations
Graph the following relations by completing the tables given. Then use the graph
to state the domain and range of the relation.
a. b. c.
Solution
䊳
For each relation, we use each x-input in turn to determine the related y-output(s),
if they exist. Results can be entered in a table and the ordered pairs used to assist
in drawing a complete graph.
a. y ⴝ x
2
2x
x y
2
y 29 x
2
y x
2
2x
y 僆 ⺢.x 僆 ⺢.
y x 1
1–5 Section 1.1 Rectangular Coordinates; Graphing Circles and Other Relations 89
College Algebra G&M—
Figure 1.11
(2, 0)
(3, 3)
(4, 8)
(2, 8)
(1, 3)
(0, 0)
(1, 1)
y x
2
2x
x
y
55
2
5
The resulting vertical parabola is shown in Figure 1.11. Although ( ) and
( ) cannot be plotted here, the arrowheads indicate an infinite extension of
the graph, which will include these points. This “infinite extension” in the upward
direction shows there is no largest y-value (the graph becomes infinitely “tall”).
Since the smallest possible y-value is [from the vertex ( )], the range is
. However, this extension also continues forever in the outward direction
as well (the graph gets wider and wider). This means the x-value of all possible
ordered pairs could vary from negative to positive infinity, and the domain is all
real numbers. We then have and .R: y 1D: x 僆 ⺢
y 1
1, 11
3, 15
4, 24
(x, y)
xyOrdered Pairs
24 ( )
15 ( )
8()
3()
0 0 (0, 0)
1 (1, )
2 0 (2, 0)
3 3 (3, 3)
4 8 (4, 8)
1
1
1, 31
2, 82
3, 153
4, 244
cob19545_ch01_085-102.qxd 11/1/10 8:52 AM Page 89
