Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.

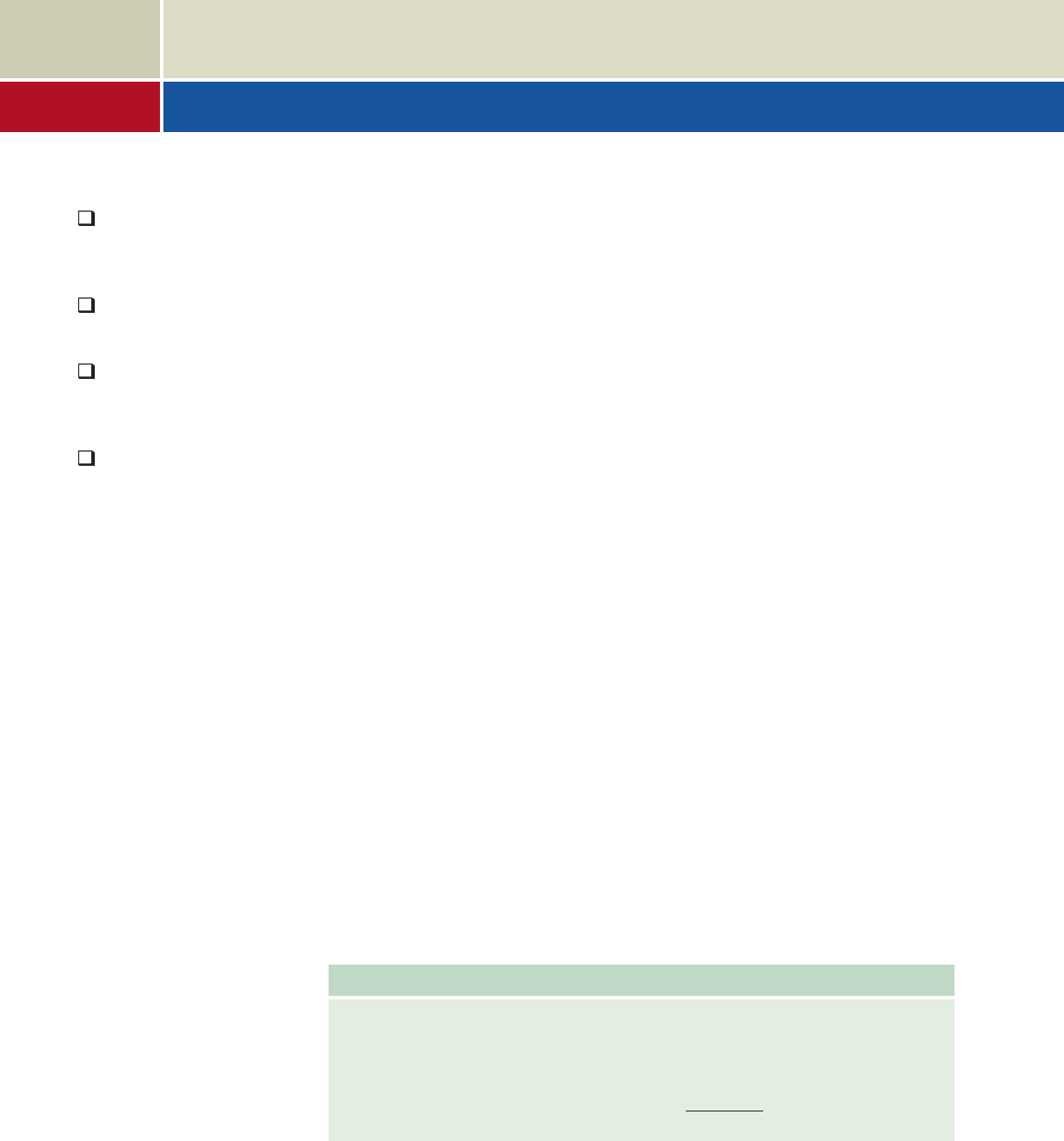
The derivation of the sum and difference identities in Section 6.3 was a “watershed
event” in the study of identities. By making various substitutions, they lead us very
naturally to many new identity families, giving us a heightened ability to simplify
expressions, solve equations, find exact values, and model real-world phenomena. In
fact, many of the identities are applied in very practical ways, as in a study of projec-
tile motion and the conic sections (Chapter 10). In addition, one of the most profound
principles discovered in the eighteenth and nineteenth centuries was that electricity,
light, and sound could all be studied using sinusoidal waves. These waves often inter-
act with each other, creating the phenomena known as reflection, diffraction, super-
position, interference, standing waves, and others. The product-to-sum and
sum-to-product identities play a fundamental role in the investigation and study of
these phenomena.
A. The Double-Angle Identities
The double-angle identities for sine, cosine, and tangent can all be derived using the
related sum identities with two equal angles We’ll illustrate the process here
for the cosine of twice an angle.
sum identity for cosine
assume and substitute for
simplify—double-angle identity for cosine
Using the Pythagorean identity we can easily find two
additional members of this family, which are often quite useful. For
we have
double-angle identity for cosine
substitute for
double-angle in terms of sine
Using we obtain an additional form:
double-angle identity for cosine
substitute for
double-angle in terms of cosine
The derivations of and are likewise developed and are asked for
in Exercise 103. The double-angle identities are collected here for your convenience.
The Double-Angle Identities
cosine: sine:
tangent:
tan122
2 tan
1 tan
2
2 cos
2
1
1 2 sin
2
sin122 2 sin cos cos122 cos
2
sin
2
tan122sin122
cos122 2 cos
2
1
sin
2
1 cos
2
cos
2
11 cos
2
2
cos122 cos
2
sin
2
sin
2
1 cos
2
cos122 1 2 sin
2
cos
2
1 sin
2
11 sin
2
2 sin
2
cos122 cos
2
sin
2
cos
2
1 sin
2
cos
2
sin
2
1,
cos122 cos
2
sin
2
cos1 2 cos cos sin sin
cos1 2 cos cos sin sin
1 2.
640 6-26
Learning Objectives
In Section 6.4 you will learn how to:
A. Derive and use the
double-angle identities
for cosine, tangent, and
sine
B. Develop and use the
power reduction and
half-angle identities
C. Derive and use the
product-to-sum and
sum-to-product
identities
D. Solve applications using
these identities
6.4 The Double-Angle, Half-Angle, and Product-to-Sum Identities
College Algebra & Trignometry—
cob19529_ch06_640-654.qxd 12/27/08 0:08 Page 640

6-27 Section 6.4 The Double-Angle, Half-Angle, and Product-to-Sum Identities 641
EXAMPLE 1
Using a Double-Angle Identity to Find Function Values
Given , find the value of
Solution
Using the double-angle identity for cosine in terms of sine, we find
double-angle in terms of sine
substitute for
result
If then
Now try Exercises 7 through 20
Like the fundamental identities, the double-angle identities can be used to
verify or develop others. In Example 2, we explore one of many multiple-angle
identities, verifying that can be rewritten as (in terms of
powers of ).
EXAMPLE 2
Verifying a Multiple Angle Identity
Verify that is an identity.
Solution
Use the sum identity for cosine, with and Note that our goal is an
expression using cosines only, with no multiple angles.
sum identity for cosine
substitute for and for
substitute for and
multiply
substitute for
multiply
combine terms
Now try Exercises 21 and 22
EXAMPLE 3
Using a Double-Angle Formula to Find Exact Values
Find the exact value of .
Solution
A product of sines and cosines having the same argument hints at the double-angle
identity for sine. Using and dividing by 2 givessin122 2 sin cos
sin 22.5° cos 22.5°
4 cos
3
3 cos
2 cos
3
cos 2 cos 2 cos
3
sin
2
1 cos
2
2 cos
3
cos 2 cos 11 cos
2
2
2 cos
3
cos 2 cos sin
2
sin122cos122
cos132 12 cos
2
12 cos 12 sin cos 2 sin
2
cos12 2 cos122 cos sin122sin
cos1 2 cos cos sin sin
. 2
cos132 4 cos
3
3 cos
cos
4 cos
3
3 cos cos132
cos122
7
32
.sin
5
8
,
7
32
2a
5
8
b
2
25
32
1
25
32
sin
5
8
1 2a
5
8
b
2
cos122 1 2 sin
2
cos122.sin
5
8
College Algebra & Trignometry—
cob19529_ch06_640-654.qxd 01/13/2009 09:47 PM Page 641 ssen 1 HD 049:Desktop Folder:Satya 13/01/09:Used file:MHDQ092-6.4:

642 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-28
double-angle identity for sine
replace with
multiply
Now try Exercises 23 through 30
B. The Power Reduction and Half-Angle Identities
Expressions having a trigonometric function raised to a power occur quite frequently
in various applications. We can rewrite even powers of these trig functions in terms of
an expression containing only cosine to the power 1, using what are called the power
reduction identities.This makes the expression easier to use and evaluate. It can legit-
imately be argued that the power reduction identities are actually members of the
double-angle family, as all three are a direct consequence. To find identities for cos
2
x
and sin
2
x, we solve the related double-angle identity involving cos (2x).
in terms of sine
subtract 1, then divide by 2
power reduction identity for sine
Using the same approach for gives The identity for
can be derived from (see Exercise 104), but in this case
it’s easier to use the identity The result is
The Power Reduction Identities
EXAMPLE 4
Using a Power Reduction Formula
Write in terms of an expression containing only cosines to the power 1.
Solution
original expression
substitute for sin
2
x
multiply
substitute for cos
2
(2x)
multiply
result
Now try Exercises 31 through 36
3 4 cos12x2 cos14x2
2 4 cos12x2 1 cos14x2
1 cos14x2
2
2c1 2 cos12x2
1 cos14x2
2
d
231 2 cos12x2 cos
2
12x24
1 cos12x2
2
8c
1 cos12x2
2
d
2
8 sin
4
x 81sin
2
x2
2
8 sin
4
x
cos
2
1 cos122
2
sin
2
1 cos122
2
tan
2
1 cos122
1 cos122
1 cos122
1 cos122
.tan
2
u
sin
2
u
cos
2
u
.
tan122
2 tan
1 tan
2
tan
2
cos
2
1 cos122
2
.cos
2
sin
2
1 cos122
2
2 sin
2
cos122 1
cos122 1 2 sin
2
cos122
sin 45°
12
2
12
2
2
12
4
sin 45°
2
22.5° sin 22.5° cos 22.5°
sin12322.5°42
2
sin cos
sin122
2
College Algebra & Trignometry—
A. You’ve just learned how
to derive and use the double-
angle identities for cosine,
tangent, and sine
cob19529_ch06_615-700.qxd 11/11/08 6:20 PM Page 642 epg HD 049:Desktop Folder:11/11/08:z_old:

6-29 Section 6.4 The Double-Angle, Half-Angle, and Product-to-Sum Identities 643
The half-angle identities follow directly from those above, using algebra and a
simple change of variable. For we first take square roots and
obtain Using the substitution gives
and making these substitutions results in the half-angle identity for cosine:
where the radical’s sign depends on the quadrant in which
terminates. Using the same substitution for sine gives
and for the tangent identity, In the case of we can
actually develop identities that are free of radicals by rationalizing the denominator
or numerator. We’ll illustrate the former, leaving the latter as an exercise (see
Exercise 102).
multiply by the conjugate
rewrite
Pythagorean identity
Since and sin u has the same sign as for all u in its domain,
the relationship can simply be written
The Half-Angle Identities
EXAMPLE 5
Using Half-Angle Formulas to Find Exact Values
Use the half-angle identities to find exact values for (a) and (b)
Solution
Noting that is one-half the standard angle we can find each value by
applying the respective half-angle identity with in Quadrant I.u 30°
30°,15°
tan 15°.sin 15°
tana
u
2
b
sin u
1 cos u
tana
u
2
b
1 cos u
sin u
tana
u
2
b
A
1 cos u
1 cos u
sina
u
2
b
A
1 cos u
2
cosa
u
2
b
A
1 cos u
2
tana
u
2
b
1 cos u
sin u
.
tana
u
2
b
1 cos u 7 0
2x
2
x
`
1 cos u
sin u
`
B
11 cos u2
2
sin
2
u
B
11 cos u2
2
1 cos
2
u
tana
u
2
b
A
11 cos u211 cos u2
11 cos u211 cos u2
tana
u
2
b,tana
u
2
b
A
1 cos u
1 cos u
.
sina
u
2
b
A
1 cos u
2
,
u
2
cosa
u
2
b
A
1 cos u
2
,
u
2
,u 2cos
A
1 cos122
2
.
cos
2
1 cos122
2
,
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 6:20 PM Page 643 epg HD 049:Desktop Folder:11/11/08:z_old:

644 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-30
a. b.
Now try Exercises 37 through 48
EXAMPLE 6
Using Half-Angle Formulas to Find Exact Values
For and in QIII, find exact values of and
Solution
With in QIII we know must be in QII and
we choose our signs accordingly: and
Now try Exercises 49 through 64
C. The Product-to-Sum Identities
As mentioned in the introduction, the product-to-sum and sum-to-product identities
are of immense importance to the study of any phenomenon that travels in waves, like
light and sound. In fact, the tones you hear as you dial a telephone are actually the sum
of two sound waves interacting with each other. Each derivation of a product-to-sum
identity is very similar (see Exercise 105), and we illustrate by deriving the identity
for Beginning with the sum and difference identities for cosine, we have
cosine of a difference
cosine of a sum
combine equations
divide by 2
The identities from this family are listed here.
cos cos
1
2
3cos1 2 cos1 24
2 cos cos cos1 2 cos1 2
cos cos sin sin
cos1 2
cos cos sin sin cos1 2
cos cos .
A
9
25
3
5
A
16
25
4
5
Q
1
a
7
25
b
2
Q
1
a
7
25
b
2
cosa
2
b
A
1 cos
2
sina
2
b
A
1 cos
2
cosa
2
b6 0.sina
2
b7 0
S
2
6
2
6
3
4
2
S 6 6
3
2
,
cosa
2
b.sina
2
bcos
7
25
sin 15°
1
2 13
2
tan 15°
1
13
2
1
2
2 13
Q
1
13
2
2
tana
30
2
b
1 cos 30
sin 30
sina
30
2
b
A
1 cos 30
2
B. You’ve just learned how
to develop and use the power
reduction and half-angle
identities
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 6:20 PM Page 644 epg HD 049:Desktop Folder:11/11/08:z_old:

6-31 Section 6.4 The Double-Angle, Half-Angle, and Product-to-Sum Identities 645
The Product-to-Sum Identities
EXAMPLE 7
Rewriting a Product as an Equivalent Sum Using Identities
Write the product 2 cos(27t) cos(15t) as the sum of two cosine functions.
Solution
This is a direct application of the product-to-sum identity, with
and
product-to-sum identity
substitute
result
Now try Exercises 65 through 73
There are times we find it necessary to “work in the other direction,” writing a sum
of two trig functions as a product. This family of identities can be derived from the
product-to-sum identities using a change of variable. We’ll illustrate the process for
You are asked for the derivation of in Exercise 106. To
begin, we use and This creates the sum and
the difference yielding and , respectively.
Dividing the original expressions by 2 gives and which all
together make the derivation a matter of direct substitution. Using these values in any
product-to-sum identity gives the related sum-to-product, as shown here.
The sum-to-product identities follow.
The Sum-to-Product Identities
cos u cos v 2 sina
u v
2
b sina
u v
2
b sin u sin v 2 cosa
u v
2
b sina
u v
2
b
sin u sin v 2 sina
u v
2
b cosa
u v
2
b cos u cos v 2 cosa
u v
2
b cosa
u v
2
b
2 sina
u v
2
b cosa
u v
2
b sin u sin v
sina
u v
2
b cosa
u v
2
b
1
2
1sin u sin v2
sin cos
1
2
3sin1 2 sin1 24
u v
2
,
u v
2
v u2 2 2v,
2 2 2u2 u v.2 u v
cos u cos vsin u sin v.
cos112t2 cos142t2
2 cos127t2cos115t2 2a
1
2
b3cos127t 15t2 cos127t 15t24
cos cos
1
2
3cos1 2 cos1 24
15t. 27t
cos sin
1
2
3sin1 2 sin1 24 sin cos
1
2
3sin1 2 sin1 24
sin sin
1
2
3cos1 2 cos1 24 cos cos
1
2
3cos1 2 cos1 24
College Algebra & Trignometry—
product-to-sum identity (sum of
sines)
substitute for , for ,
substitute u for and v for
multiply by 2
u v
2
u v
2
cob19529_ch06_615-700.qxd 11/11/08 6:20 PM Page 645 epg HD 049:Desktop Folder:11/11/08:z_old:

646 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-32
EXAMPLE 8
Rewriting a Sum as an Equivalent Product Using Identities
Given and express as a product of
trigonometric functions.
Solution
This is a direct application of the sum-to-product identity with
and
Now try Exercises 74 through 82
For a mixed variety of identities, see Exercises 83–100.
D. Applications of Identities
In more advanced mathematics courses, rewriting an expression using identities
enables the extension or completion of a task that would otherwise be very difficult
(or even impossible). In addition, there are a number of practical applications in the
physical sciences.
Projectile Motion
A projectile is any object that is thrown, shot, kicked, dropped, or otherwise given an
initial velocity, but lacking a continuing source of propulsion. If air resistance is
ignored, the range of the projectile depends only on its initial velocity v and the angle
at which it is propelled. This phenomenon is modeled by the function
EXAMPLE 9
Using Identities to Solve an Application
a. Use an identity to show is equivalent to
b. If the projectile is thrown with an initial velocity of ft/sec, how far will
it travel if ?
c. From the result of part (a), determine what angle will give the maximum
range for the projectile.
Solution
a. Note that we can use a double-angle identity if we rewrite the coefficient.
Writing as and commuting the factors gives
b. With ft/sec and , the formula gives
Evaluating the result shows the projectile travels a horizontal distance of 144 ft.
r 115°2 a
1
32
b1962
2
sin 30°. 15°v 96
r12 a
1
32
bv
2
12 sin cos 2 a
1
32
b v
2
sin122.
2a
1
32
b
1
16
15°
v 96
r12
1
32
v
2
sin122.
r12
1
16
v
2
sin cos
r 12
1
16
v
2
sin cos .
2 sin111t2 cos1t2
sin112t2 sin110t2 2 sina
12t 10t
2
b cosa
12t 10t
2
b
sin u sin v 2 sina
u v
2
b cosa
u v
2
b
v 10t.u 12t
sin u sin v,
y
1
y
2
y
2
sin110t2,y
1
sin112t2
C. You’ve just learned how
to derive and use the
product-to-sum and sum-
to-product identities
sum-to-product identity
substitute for
u and for v
substitute
10t
12t
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 6:20 PM Page 646 epg HD 049:Desktop Folder:11/11/08:z_old:
6-33 Section 6.4 The Double-Angle, Half-Angle, and Product-to-Sum Identities 647
c. For any initial velocity v, will be maximized when is a maximum.
This occurs when , meaning and The maximum
range is achieved when the projectile is released at an angle of
Now try Exercises 109 and 110
45°.
45°.2 90°sin122 1
sin122r12
GRAPHICAL SUPPORT
The result in Example 9(c) can be verified
graphically by assuming an initial velocity
of 96 ft/sec and entering the function
as Y
1
on a
graphing calculator. With an amplitude of 288
and results confined to the first quadrant, we
set an appropriate window, graph the function,
and use the (CALC 4:maximum)
feature. As shown in the figure, the max occurs at 45°.
TRACE
2nd
r12
1
32
1962
2
sin122 288 sin122
300
0
900
Sound Waves
Each tone you hear on a touch-tone phone is actually the combination of precisely two
sound waves with different frequencies (frequency f is defined as ). This is why
the tones you hear sound identical, regardless of what phone you use. The sum-
to-product and product-to-sum formulas help us to understand, study, and use sound in
very powerful and practical ways, like sending faxes and using other electronic media.
EXAMPLE 10
Using an Identity to Solve an Application
On a touch-tone phone, the sound created by
pressing 5 is produced by combining a sound
wave with frequency 1336 cycles/sec, with
another wave having frequency 770 cycles/sec.
Their respective equations are
and with
the resultant wave being or
Rewrite this
sum as a product.
Solution
This is a direct application of the sum-to-product identity, with and
Computing one-half the sum/difference of u and v gives
and
sum-to-product identity
Now try Exercises 111 and 112
Note we can identify the button pressed when the wave is written as a sum. If we
have only the resulting wave (written as a product), the product-to-sum formula must
be used to identify which button was pressed.
Additional applications requiring the use of identities can be found in Exercises
113 through 117.
cos12672t2 cos11540t2 2 cos12106t2cos1566t2
cos u cos v 2 cosa
u v
2
b cosa
u v
2
b
2672t 1540t
2
566t.
2672t 1540t
2
2106t
v 1540t.
u 2672t
y cos12672t2 cos11540t2.
y y
1
y
2
y
2
cos12 770t2,y
1
cos12 1336t2
f
B
2
substitute for u
and for v1540t
2672t
D. You’ve just learned how
to solve applications using
identities
College Algebra & Trignometry—
1
1209 cps
23
456
789
*
0#
1477 cps
697 cps
770 cps
852 cps
941 cps
1336 cps
cob19529_ch06_615-700.qxd 11/11/08 6:20 PM Page 647 epg HD 049:Desktop Folder:11/11/08:z_old:
6.4 EXERCISES
648 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-34
CONCEPTS AND VOCABULARY
Fill in each blank with the appropriate word or phrase.
Carefully reread the section if needed.
1. The double-angle identities can be derived using
the identities with For we
expand using .
2. If is in QIII then and must be
in since .
3. Multiple-angle identities can be derived using the
sum and difference identities. For sin (3x) use sin
( ).
6
2
6
2
180° 6 6 270°
cos1 2
cos122 .
4. For the half-angle identities the sign preceding the
radical depends on the in which .
5. Explain/Discuss how the three different identities
for are related. Verify that
6. In Example 6, we were given and
in QIII. Discuss how the result would differ if we
stipulate that is in QII instead.
cos
7
25
1 cos x
sin x
sin x
1 cos x
.
tana
u
2
b
u
2
DEVELOPING YOUR SKILLS
Find exact values for sin(2 ), cos(2 ), and tan(2 ) using
the information given.
7. ; in QII 8. ; in QII
9. in QII 10. ; in QIII
11. in QIII 12. in QI
13. ;
14. ;
15. ;
16.
Find exact values for , and tan using the
information given.
17. in QII
18. ; in QIII2sin122
240
289
2sin122
24
25
;
sin , cos
cos 7 0cot
80
39
;
sec 6 0csc
5
3
tan 7 0cos
8
17
cos 6 0sin
48
73
sec
53
28
;tan
13
84
;
sin
63
65
cos
9
41
;
cos
21
29
sin
5
13
19. ; in QII
20. ; in QIV
21. Verify the following identity:
22. Verify the following identity:
Use a double-angle identity to find exact values for the
following expressions.
23. 24.
25. 26.
27. 28.
29. Use a double-angle identity to rewrite
9 sin (3x) cos (3x) as a single function.
[Hint: .]
30. Use a double-angle identity to rewrite
as a single term.
[Hint: Factor out a constant.]
2.5 5 sin
2
x
9
9
2
122
2 tan 1
12
2
1 tan
2
1
12
2
2 tan 22.5°
1 tan
2
22.5°
2 cos
2
a
12
b 11 2 sin
2
a
8
b
cos
2
15° sin
2
15°cos 75° sin 75°
cos142 8 cos
4
8 cos
2
1
sin132 3 sin 4 sin
3
2cos122
120
169
2cos122
41
841
College Algebra & Trignometry—
cob19529_ch06_640-654.qxd 12/26/08 20:25 Page 648

Rewrite in terms of an expression containing only
cosines to the power 1.
31. sin
2
x cos
2
x 32. sin
4
x cos
2
x
33. 3 cos
4
x 34. cos
4
x sin
4
x
35. 2 sin
6
x 36. 4 cos
6
x
Use a half-angle identity to find exact values for
, and for the given value of .
37. 38.
39. 40.
41. 42.
43. 44.
Use the results of Exercises 37–40 and a half-angle
identity to find the exact value.
45. 46.
47. 48.
Use a half-angle identity to rewrite each expression as a
single, nonradical function.
49. 50.
51. 52.
53. 54.
Find exact values for and
using the information given.
55. ; is obtuse
56. ; is obtuse
57. ; in QII
58. ; in QIII
59. ; in QIItan
35
12
sin
7
25
cos
4
5
cos
8
17
sin
12
13
tan a
2
bsin a
2
b, cos a
2
b,
1211 cos x2
1 cos x
sin12x2
1 cos12x2
1 cos16x2
sin16x2A
1 cos142
1 cos142
A
1 cos 45°
2A
1 cos 30°
2
cosa
5
24
bsina
24
b
tan 37.5°sin 11.25°
11
12
3
8
112.5° 67.5°
5
12
12
75° 22.5°
tan sin , cos
60. ; in QIII
61. ; is acute
62. ; is acute
63.
64.
Write each product as a sum using the product-to-sum
identities.
65. 66.
67. 68.
69.
70.
Find the exact value using product-to-sum identities.
71.
72. 73.
Write each sum as a product using the sum-to-product
identities.
74. 75.
76. 77.
78.
79.
Find the exact value using sum-to-product identities.
80.
81.
82.
Verify the following identities.
83.
84.
1 2 sin
2
x
2 sin x cos x
cot12x2
2 sin x cos x
cos
2
x sin
2
x
tan12x2
sina
11
12
b sina
7
12
b
sina
17
12
b sina
13
12
b
cos 75° cos 15°
cos1852t2 cos11209t2
cos1697t2 cos 11447t2
cosa
7x
6
b cosa
5x
6
bsina
11x
8
b sina
5x
8
b
sin114k2 sin141k2cos19h2 cos14h2
sina
7
12
b sina
12
bsina
7
8
b cosa
8
b
2 cos 15° sin 135°
2 cos12150t2 cos1268t2
2 cos11979t2 cos1439t2
2 sina
5t
2
b sina
9t
2
b2 cosa
7t
2
b cosa
3t
2
b
cos1152 sin132sin142 sin182
csc
41
9
;
2
6 6
cot
21
20
; 6 6
3
2
cos
48
73
sin
15
113
sec
65
33
6-35 Section 6.4 The Double-Angle, Half-Angle, and Product-to-Sum Identities 649
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 6:20 PM Page 649 epg HD 049:Desktop Folder:11/11/08:z_old:
