Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.


85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97. 1 sin
2
122 1 4 sin
2
4 sin
4
1 2 sin
2
a
x
4
b cosa
x
2
b
cos
2
a
x
2
b sin
2
a
x
2
b cos x
csc 12x2
1
2
csc x sec x
tan x cot x 2 csc 12x2
cot tan
2 cos 122
sin 122
tan 122
2
cot tan
csc
2
2
cos 122
sin
2
cos 122
sin
2
cot
2
1
sin 14x2 4 sin x cos x11 2 sin
2
x2
cos182 cos
2
142 sin
2
142
1sin
2
x 12
2
sin
4
x cos 12x2
1sin x cos x2
2
1 sin 12x2
98.
99.
100.
101. Show .
102. Show that is equivalent
to by rationalizing the numerator.
103. Derive the identity for and using
and where .
104. Derive the identity for using
Hint: Solve for and
work in terms of sines and cosines.
105. Derive the product-to-sum identity for .
106. Derive the sum-to-product identity for
.cos u cos v
sin sin
tan
2
tan122
2 tan12
1 tan
2
12
.
tan
2
12
tan 1 2,sin 1 2
tan 122sin 122
sin u
1 cos u
tana
u
2
b
A
1 cos u
1 cos u
sin
2
11 cos 2
2
c2 sina
2
bd
2
sin m sin n
cos m cos n
tana
m n
2
b
sin1120t2 sin180t2
cos1120t2 cos180t2
cot120t2
2 cos
2
a
x
2
b 1 cos x
650 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-36
WORKING WITH FORMULAS
107. Supersonic speeds, the sound barrier, and Mach
numbers:
The speed of sound varies with temperature and
altitude. At , sound travels about 742 mi/hr at
sea level. A jet-plane flying faster than the speed of
sound (called supersonic speed) has “broken the
sound barrier.” The plane projects three-
dimensional sound waves about the nose of the craft
that form the shape of a cone. The cone intersects
the Earth along a hyperbolic path, with a sonic
boom being heard by anyone along this path. The
ratio of the plane’s speed to the speed of sound is
32°F
M csc a
2
b
called its Mach number M, meaning a plane flying
at is traveling 3.2 times the speed of
sound. This Mach number can be determined using
the formula given here, where is the vertex angle
of the cone described. For the following exercises,
use the formula to find or as required. For
parts (a) and (b), answer in exact form (using a
half-angle identity) and approximate form.
a. b. c.
108. Malus’s law:
When a beam of plane-polarized light with
intensity I
0
hits an analyzer, the intensity I of the
transmitted beam of light can be found using the
formula shown, where is the angle formed
between the transmission axes of the polarizer and
the analyzer. Find the intensity of the beam when
and candelas (cd). Answer in
exact form (using a power reduction identity) and
approximate form.
I
0
300 15°
I I
0
cos
2
M 2 45° 30°
M
M 3.2
College Algebra & Trignometry—
cob19529_ch06_640-654.qxd 12/29/2008 09:11 am Page 650
6-37 Section 6.4 The Double-Angle, Half-Angle, and Product-to-Sum Identities 651
APPLICATIONS
Range of a projectile: Exercises 109 and 110 refer to
Example 9. In Example 9, we noted that the range of a
projectile was maximized at . If or
, the projectile falls short of its maximum potential
distance. In Exercises 109 and 110 assume that the
projectile has an initial velocity of 96 ft/sec.
109. Compute how many feet short of maximum the
projectile falls if (a) and (b) .
Answer in both exact and approximate form.
110. Use a calculator to compute how many feet short of
maximum the projectile falls if (a) and
and (b) and . Do you
see a pattern? Discuss/explain what you notice and
experiment with other values to confirm your
observations.
Touch-tone phones: The diagram given in Example 10
shows the various frequencies used to create the tones for a
touch-tone phone. One button is randomly pressed and the
resultant wave is modeled by y(t) shown. Use a product-to-
sum identity to write the expression as a sum and determine
the button pressed.
111.
112.
113. Clock angles: Kirkland
City has a large clock
atop city hall, with a
minute hand that is 3 ft
long. Claire and Monica
independently attempt to
devise a function that
will track the distance
between the tip of the
minute hand at t minutes between the hours, and
the tip of the minute hand when it is in the
vertical position as shown. Claire finds the
function , while Monica devises
. Use the identities
from this section to show the functions are
equivalent.
114. Origami: The
Japanese art of
origami involves the
repeated folding of a
single piece of paper
to create various art
forms. When the
upper right corner of
d1t2
A
18
c
1 cos
a
t
30
bd
d1t2 `6 sina
t
60
b`
y 1t2 2 cos 11906t2cos 1512t2
y 1t2 2 cos 12150t2cos 1268t2
52.5° 37.5° 50°
40°
67.5° 22.5°
6 45°
7 45°
45°
a rectangular 21.6-cm by 28-cm piece of paper
is folded down until the corner is flush with the
other side, the length L of the fold is
related to the angle by . (a) Show
this is equivalent to , (b) find the
length of the fold if and (c) find the angle
if .
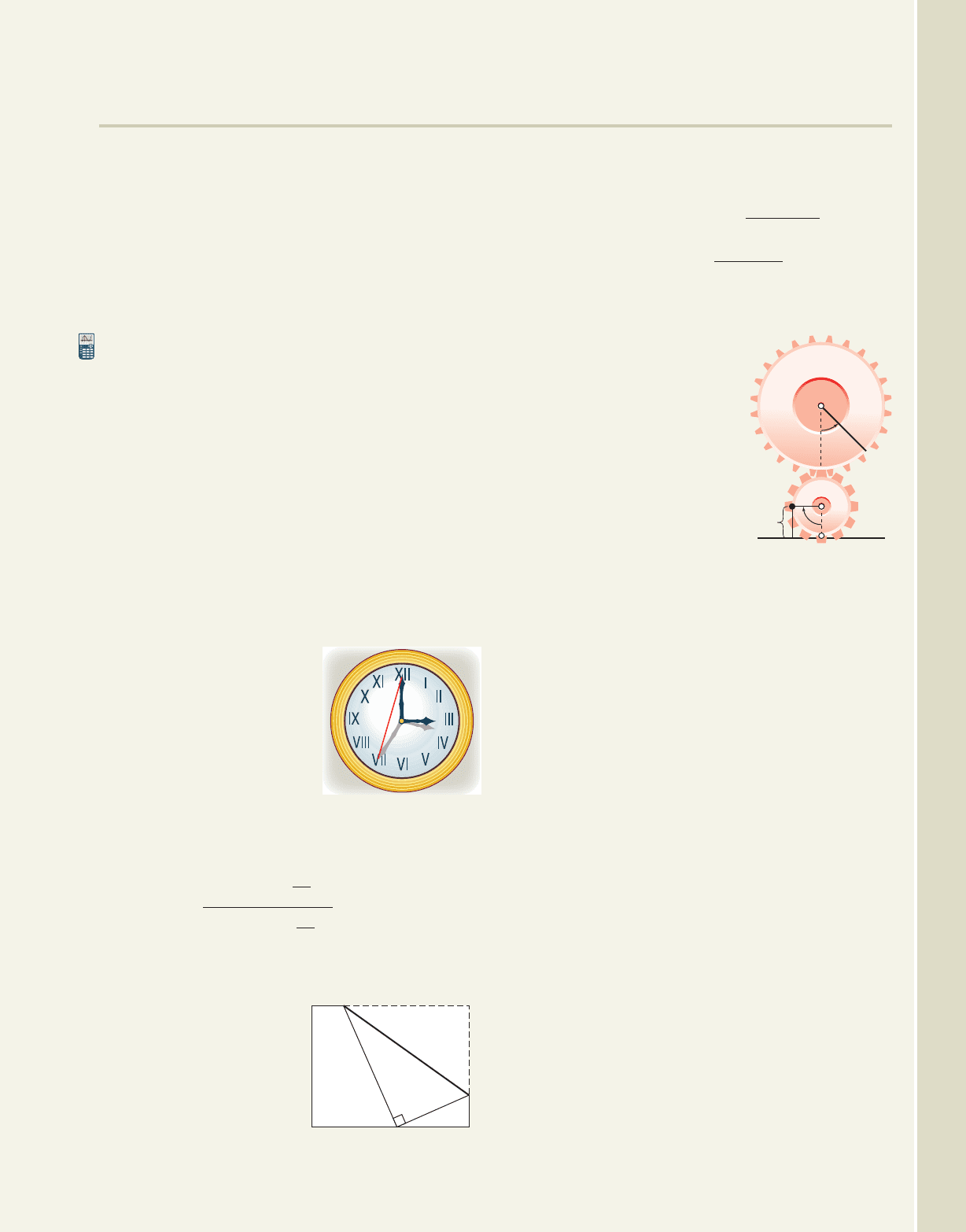
115. Machine gears: A machine
part involves two gears.
The first has a radius of 2 cm
and the second a radius of
1 cm, so the smaller gear
turns twice as fast as the
larger gear. Let represent
the angle of rotation in the
larger gear, measured from
a vertical and downward
starting position. Let P be a
point on the circumference
of the smaller gear, starting at the vertical and
downward position. Four engineers working on
an improved design for this component devise
functions that track the height of point P above
the horizontal plane shown, for a rotation of
by the larger gear. The functions they develop
are: Engineer A:
Engineer B: Engineer C:
and Engineer D:
Use any of the identities
you’ve learned so far to show these four
functions are equivalent.
116. Working with identities: Compute the value of
two ways, first using the half-angle identity
for sine, and second using the difference identity
for sine. (a) Find a decimal approximation for each
to show the results are equivalent and (b) verify
algebraically that they are equivalent. (Hint:
Square both sides.)
117. Working with identities: Compute the value of
two ways, first using the half-angle identity
for cosine, and second using the difference identity
for cosine. (a) Find a decimal approximation for
each to show the results are equivalent and
(b) verify algebraically that they are equivalent.
(Hint: Square both sides.)
cos 15°
sin 15°
h12 1 cos 122.
k12 1 sin
2
cos
2
;
g12 2 sin
2
;
f 12 sin 12 90°2 1;
°
L 28.8 cm
30°,
L
21.6 sec
sin122
L
10.8
sin cos
2
d
28 cm
L
21.6 cm
2 cm
1 m
P
h
2
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 6:20 PM Page 651 epg HD 049:Desktop Folder:11/11/08:z_old:
6. Verify each identity.
a.
b.
7. Given and are obtuse angles with
and , find
a.
b.
c. tan 1 2
cos 1 2
sin 1 2
tan
80
39
sin
56
65
cot x tan x
csc x sec x
cos
2
x sin
2
x
sec
2
x tan
2
x
sec
2
x
cos
2
x
652 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-38
EXTENDING THE CONCEPT
118. Can you find three distinct, real numbers whose
sum is equal to their product? A little known fact
from trigonometry stipulates that for any triangle,
the sum of the tangents of the angles is equal to the
products of their tangents. Use a calculator to test
this statement, recalling the three angles must sum
to . Our website at www.mhhe.com/coburn
shows a method that enables you to verify the
statement using tangents that are all rational values.
119. A proof without
words: From
elementary
geometry we have
the following:
(a) an angle
inscribed in a
semicircle is a right
angle; and (b) the
measure of an
180°
inscribed angle (vertex on the circumference) is
one-half the measure of its intercepted arc.
Discuss/explain how the unit-circle diagram offers
a proof that . Be detailed and
thorough.
120. Using and repeatedly applying the half-
angle identity for cosine, show that is
equal to . Verify the result
using a calculator, then use the patterns noted to
write the value of in closed form (also
verify this result). As becomes very small, what
appears to be happening to the value of ?cos
cos 1.875°
1
2 12 12
13
2
cos 3.75°
30°
tana
x
2
b
sin x
1 cos x
MAINTAINING YOUR SKILLS
121. (3.3) Use the rational roots theorem to find all
zeroes of .
122. (5.1) The hypotenuse of a certain right triangle is
twice the shortest side. Solve the triangle.
123. (5.3) Verify that is on the unit circle, then
find and to verify .1 tan
2
sec
2
sec tan
1
16
65
,
63
65
2
x
4
x
3
8x
2
6x 12 0
124. (5.5) Write the equation of
the function graphed in
terms of a sine function of
the form
.y A sin 1Bx C2 D
1
1
cos
sin
s
2
3
2
1
1
2
3
y
x
2
MID-CHAPTER CHECK
1. Verify the identity using a multiplication:
2. Verify the identity by factoring:
3. Verify the identity by combining terms:
4. Show the equation given is not an identity.
5. Verify each identity.
a.
b.
1 sec x
csc x
1 cos x
cot x
0
sin
3
x cos
3
x
sin x cos x
1 sin x cos x
1 sec
2
x tan
2
x
2 sin x
sec x
cos x
csc x
cos x sin x
cos
2
x cot
2
x cos
2
x cot
2
x
sin x 1csc x sin x2 cos
2
x
College Algebra & Trignometry—
Exercise 119
cob19529_ch06_615-700.qxd 11/11/08 6:20 PM Page 652 epg HD 049:Desktop Folder:11/11/08:z_old:
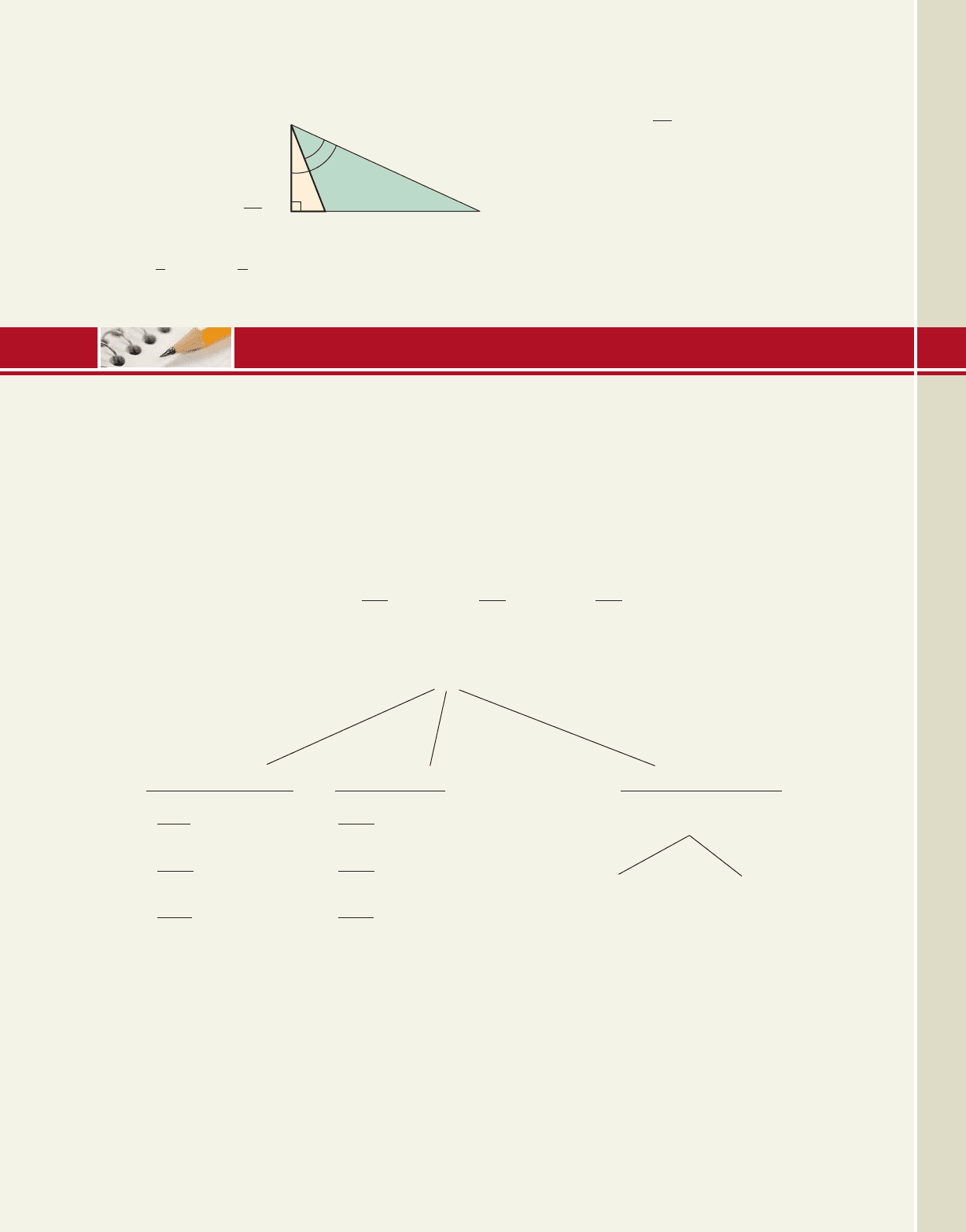
8. Use the diagram
shown to compute
sin A, cos A, and
tan A.
9. Given
and in QII, find exact values of
and .
cosa
2
bsina
2
b
cos
15
17
10. Given with in QIII, find the value of
, and .tan122sin 122, cos 122
sin
7
25
6-39 Reinforcing Basic Concepts 653
48
14
60⬚
A
REINFORCING BASIC CONCEPTS
It is a well-known fact that information is retained longer and used more effectively when it is organized, sequential, and
connected. In this Strengthening Core Skills (SCS), we attempt to do just that with our study of identities. In flowchart
form we’ll show that the entire range of identities has only two tiers, and that the fundamental identities and the sum and
difference identities are really the keys to the entire range of identities. Beginning with the right triangle definition of
sine, cosine, and tangent, the reciprocal identities and ratio identities are more semantic (word related) than mathe-
matical, and the Pythagorean identities follow naturally from the properties of right triangles. These form the first tier.
Identities—Connections and Relationships
Basic Definitions
Fundamental Identities
defined defined derived
Recipr
ocal Identities Ratio Identities Pythagorean Identities
(divide by ) (divide by )
sin
2
cos
2
sec
csc
tan
1
tan
cot
1 cot
2
csc
2
tan
2
1 sec
2
cos
sin
cot
1
cos
sec
sin
2
cos
2
1
sin
cos
tan
1
sin
csc
tan
opp
adj
cos
adj
hyp
sin
opp
hyp
College Algebra & Trignometry—
The reciprocal and ratio identities are actually defined, while the Pythagorean identities are derived from these two
families. In addition, the identity is the only Pythagorean identity we actually need to memorize; the
other two follow by division of and as indicated.
In virtually the same way, the sum and difference identities for sine and cosine are the only identities that need to be
memorized, as all other identities in the second tier flow from these.
sin
2
cos
2
sin
2
cos
2
1
Exercise 8
cob19529_ch06_640-654.qxd 12/26/08 20:33 Page 653

654 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-40
Double-Angle Identities Power Reduction Identities Half-Angle Identities Product-to-Sum Identities
use solve for in solve for combine various
in sum identities related identity and use in the sum/difference identities
power reduction identities
see Section 6.4
see Section 6.4
(use ) (use )
cos
2
1 sin
2
sin
2
1 cos
2
cos 122 1 2 sin
2
cos 122 2 cos
2
1
sina
u
2
b
A
1 cos u
2
sin
2
1 cos 122
2
cos122 cos
2
sin
2
cosa
u
2
b
A
1 cos u
2
cos
2
1 cos122
2
sin122 2 sin cos
u/2
cos122
cos , sin cos
2
, sin
2
Exercise 1: Starting with the identity
derive the other two Pythagorean identities.
sin
2
cos
2
1,
Exercise 2: Starting with the identity
derive the double-angle identities for cosine.
cos sin sin ,cos1 2 cos
College Algebra & Trignometry—
6.5 The Inverse Trig Functions and Their Applications
Learning Objectives
In Section 6.5 you will learn how to:
A. Find and graph the
inverse sine function
and evaluate related
expressions
B. Find and graph the
inverse cosine and
tangent functions and
evaluate related
expressions
C. Apply the definition and
notation of inverse trig
functions to simplify
compositions
D. Find and graph inverse
functions for sec x,
csc x, and cot x
E. Solve applications
involving inverse
functions
While we usually associate the number with the features of a circle, it also occurs
in some “interesting” places, such as the study of normal (bell) curves, Bessel func-
tions, Stirling’s formula, Fourier series, Laplace transforms, and infinite series. In
much the same way, the trigonometric functions are surprisingly versatile, finding their
way into a study of complex numbers and vectors, the simplification of algebraic
expressions, and finding the area under certain curves—applications that are hugely
important in a continuing study of mathematics. As you’ll see, a study of the inverse
trig functions helps support these fascinating applications.
A. The Inverse Sine Function
In Section 4.1 we established that only one-to-one functions have an inverse. All six
trig functions fail the horizontal line test and are not one-to-one as given. However,
by suitably restricting the domain, a one-to-one function can be defined that makes
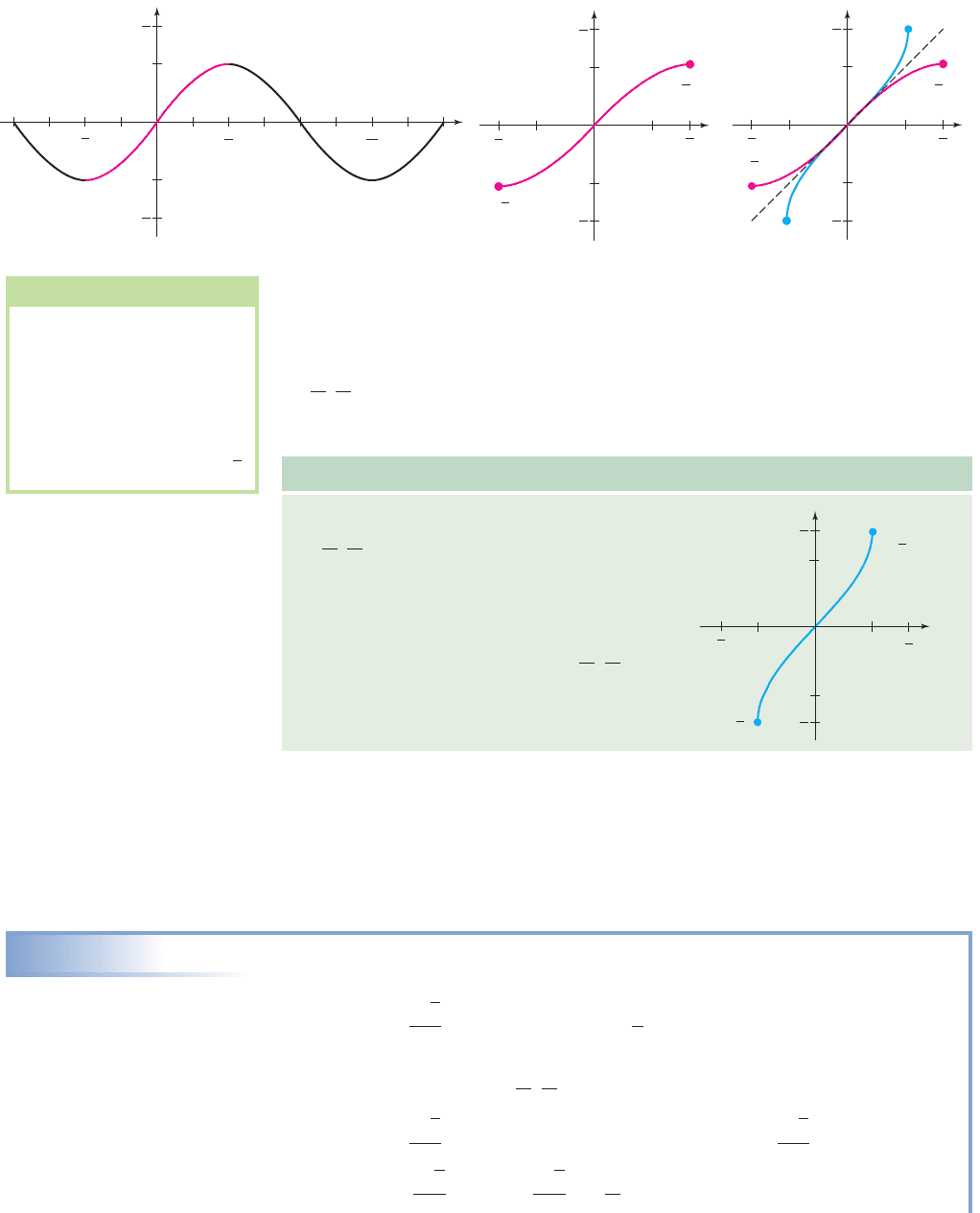
finding an inverse possible. For the sine function, it seems natural to choose
the interval since it is centrally located and the sine function attains all
possible range values in this interval. A graph of is shown in Figure 6.5, with
the portion corresponding to this interval colored in red. Note the range is still
(Figure 6.6).
31, 14
y sin x
c
2
,
2
d
Sum/Difference Identities
sin 1 2 sin cos cos sin
cos 1 2 cos cos sin sin
cob19529_ch06_640-654.qxd 1/19/09 19:12 Page 654 User-S178 MAC-OSX_1:broker:MH-DUBUQUE:MHDQ092:MHDQ092-6.4:MHDQ092-6.4:
6-41 Section 6.5 The Inverse Trig Functions and Their Applications 655
x
y
1
y sin x
2
2
2
2
1
23
2
x
y
1
11
y sin x
2
2
2
2
1
, 1
2
, 1
2
Figure 6.5 Figure 6.6
x
y
1
11
y sin
1
x
y sin x
y
x
2
2
2
2
1
, 1
2
, 1
2
Figure 6.7
WORTHY OF NOTE
In Example 4 of Section 4.1,
we noted that by suitably
restricting the domain of
a one-to-one function
could be defined that made
finding an inverse function
possible. Specifically, for
f1x2 x
2
; x 0, f
1
1x2 1x.
y x
2
,
We can obtain an implicit equation for the inverse of by interchanging
x- and y-values, obtaining By accepted convention, the explicit form of the
inverse sine function is written or Since domain and range
values have been interchanged, the domain of is and the range is
The graph of can be found by reflecting the portion in red across
the line and using the endpoints of the domain and range (see Figure 6.7).
The Inverse Sine Function
For with domain
and range
the inverse sine function is
or
with domain and range
if and only if
From the implicit form we learn to interpret the inverse function as, “y
is the number or angle whose sine is x.” Learning to read and interpret the explicit form
in this way will be helpful. That is, means “y is the number or angle whose
sine is x.”
EXAMPLE 1
Evaluating Using Special Values
Evaluate the inverse sine function for the values given:
a. b. c.
Solution
For x in and y in
a. y is the number or angle whose sine is
so
sin
1
a
13
2
b
3
.1 sin y
13
2
,
13
2
y sin
1
a
13
2
b:
c
2
,
2
d,31, 14
y sin
1
2y arcsina
1
2
by sin
1
a
13
2
b
y sin
1
x
x sin y 3 y sin
1
xy sin
1
x 3 x sin y
y sin
1
x
x sin y,
sin y xy sin
1
x
c
2
,
2
d.31, 14
y arcsin x,y sin
1
x
31, 14,c
2
,
2
d
y sin x
y x
y sin
1
xc
2
,
2
d.
31, 14y sin
1
x
y arcsin x.y sin
1
x
x sin y.
y sin x
x
y
1
1
1
1
y
sin
1
x
2
2
2
2
2
1,
2
1,
College Algebra & Trignometry—
cob19529_ch06_655-670.qxd 12/26/08 21:07 Page 655
656 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-42
b. y is the arc or angle whose sine is
so
c. y is the number or angle whose sine is 2
Since 2 is not in is undefined.
Now try Exercises 7 through 12
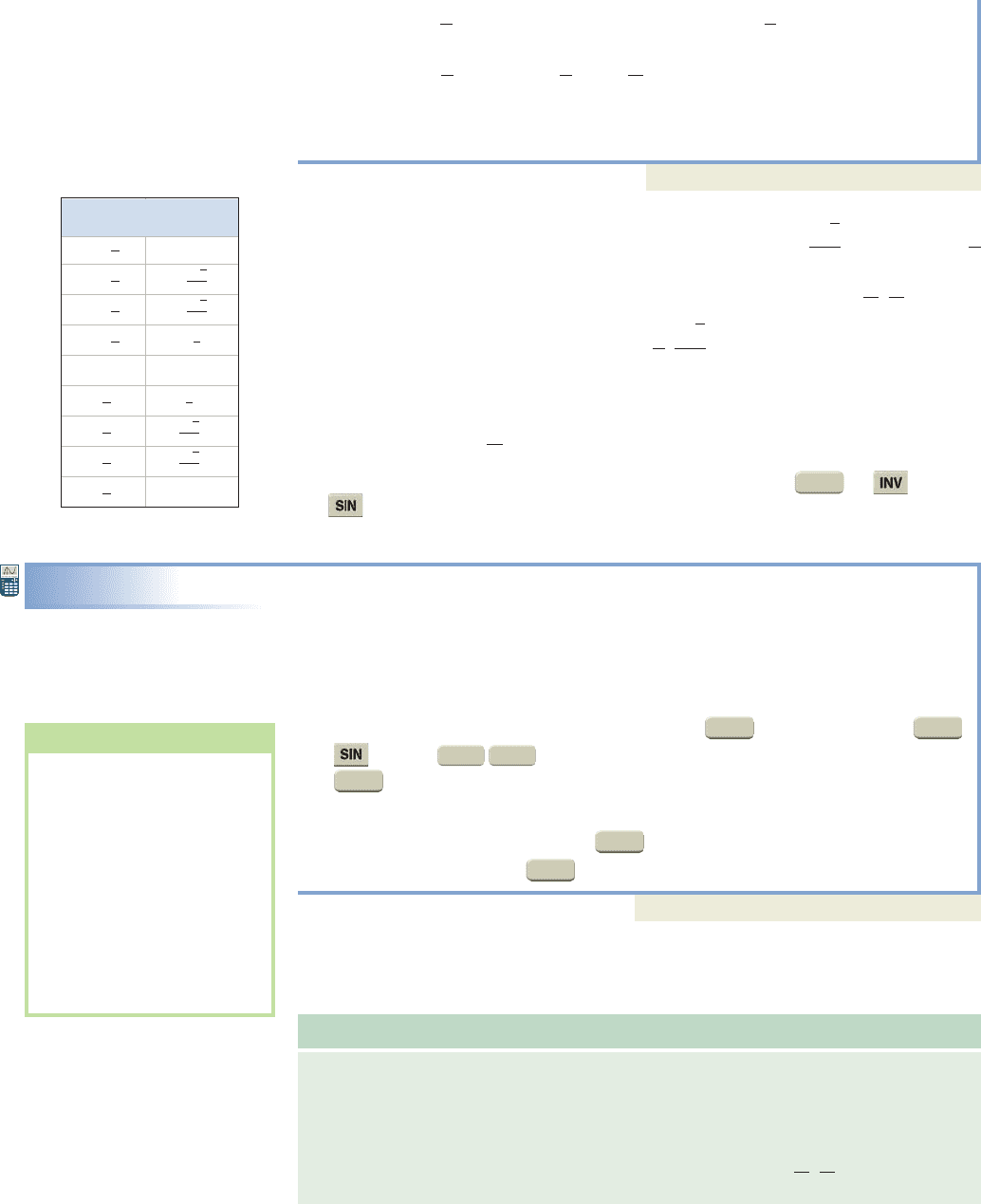
In Examples 1a and 1b, note that the equations and
each have an infinite number of solutions, but only one solution in
When x is one of the standard values can be
evaluated by reading a standard table “in reverse.” For we locate the
number in the right-hand column of Table 6.1, and note the “number or angle
whose sine is ” is If x is between and 1 but is not a standard value, we can
use the function on a calculator, which is most often the or function
for .
EXAMPLE 2
Evaluating Using a Calculator
Evaluate each inverse sine function twice. First in radians rounded to four decimal
places, then in degrees to the nearest tenth.
a. b.
Solution
For x in we evaluate
a. With the calculator in radian , use the keystrokes
0.8492 . We find radians. In degree
, the same sequence of keystrokes gives (note
that .
b. In radian , we find
. In degree ,
Now try Exercises 13 through 16
From our work in Section 4.1, we know that if f and g are inverses, and
This suggests the following properties.
Inverse Function Properties for Sine
For and
I. for x in
and
II. for x in c
2
,
2
d1g f 21x2 sin
1
1sin x2 x
31, 141f g21x2 sin 1sin
1
x2 x
g1x2 sin
1
x:f 1x2 sin x
1g f 21x2 x.
1f g21x2 x
sin
1
10.23172 13.4°.
MODE
0.2338 rad
sin
1
10.23172
MODE
y arcsin 10.23172:
1.0145 rad 58.1°2
sin
1
10.84922 58.1°
MODE
sin
1
10.84922 1.0145
ENTER
)
2ndMODE
y sin
1
0.8492:
y sin
1
x.31, 14,
y arcsin 10.23172y sin
1
0.8492
y sin
1
x
2nd
sin
1
1
2
.1,
1
y arcsin 112,
y sin
1
xa0,
1
2
,
13
2
, 1, and so onb,
c
2
,
2
d.
sin y
1
2
sin y
13
2
31, 14, sin
1
1221 sin y 2.
y sin
1
122:
arcsin a
1
2
b
6
.1 sin y
1
2
,
1
2
y arcsina
1
2
b:
Table 6.1
x sin x
00
1
2
13
2
3
12
2
4
1
2
6
1
2
6
12
2
4
13
2
3
1
2
WORTHY OF NOTE
The notation for the
inverse sine function is a
carryover from the
notation for a general inverse
function, and likewise has
nothing to do with the recip-
rocal of the function. The
arcsin x notation derives from
our work in radians on the
unit circle, where
can be interpreted as “y is an
arc whose sine is x.”
y arcsin x
f
1
1x2
sin
1
x
College Algebra & Trignometry—
cob19529_ch06_655-670.qxd 11/12/08 4:20 AM Page 656 epg HD 049:Desktop Folder:Satya 11/10/08:
6-43 Section 6.5 The Inverse Trig Functions and Their Applications 657
EXAMPLE 3
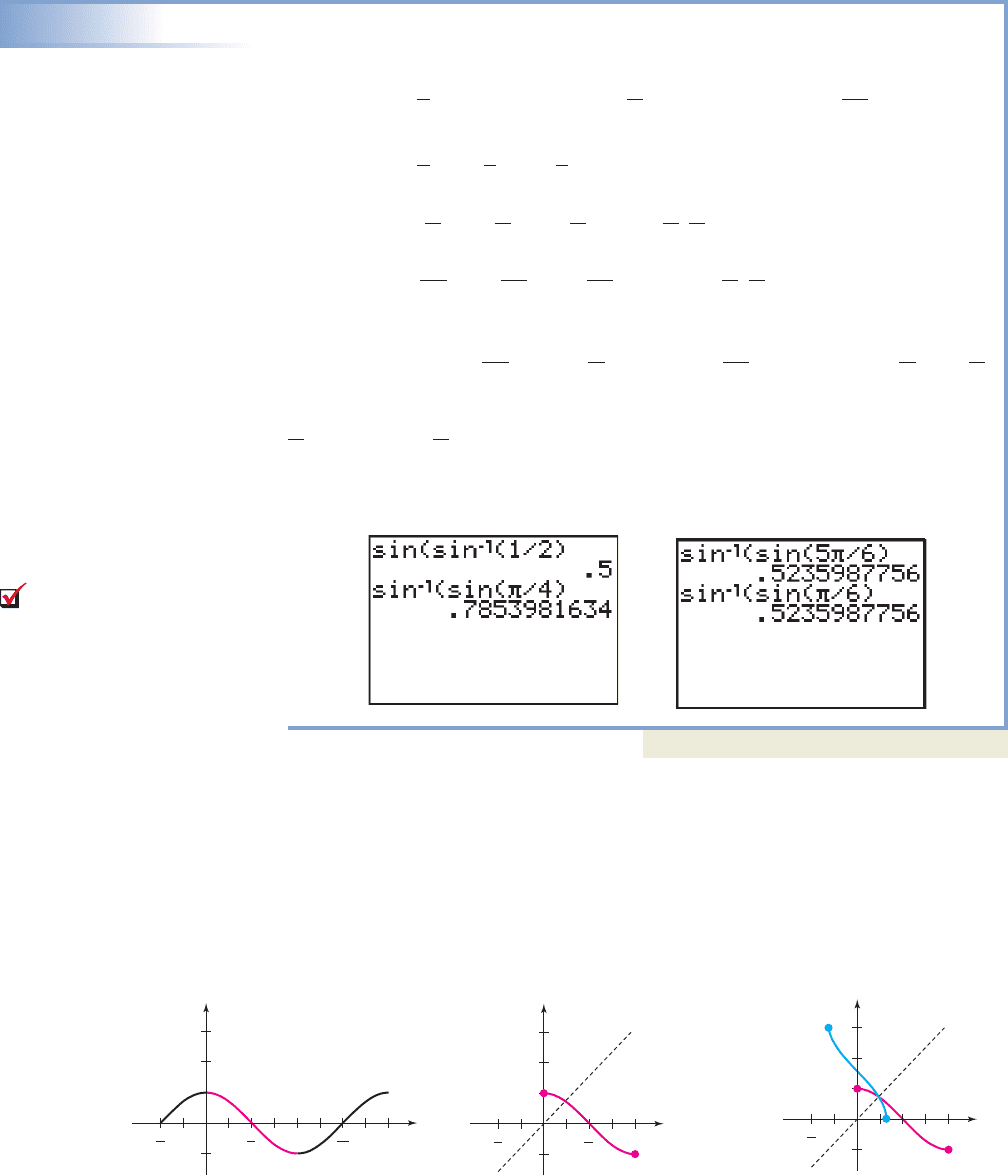
Evaluating Expressions Using Inverse Function Properties
Evaluate each expression and verify the result on a calculator.
a. b. c.
Solution
a. since is in Property I
b. since is in Property II
c. since is not in
This doesn’t mean the expression cannot be evaluated, only that we cannot use
Property II. Since
The calculator verification for each is shown in Figures 6.8 and 6.9. Note
and
4
0.7854.
6
0.5236
sina
5
6
b sina
6
b, sin
1
casin
5
6
bd sin
1
csina
6
bd
6
.
c
2
,
2
d.
5
6
sin
1
csina
5
6
bd
5
6
,
c
2
,
2
d
4
arcsincsina
4
bd
4
,
31, 14
1
2
sincsin
1
a
1
2
bd
1
2
,
sin
1
csina
5
6
bdarcsincsina
4
bdsincsin
1
a
1
2
bd
Figure 6.8
Parts (a) and (b)
Figure 6.9
Part (c)
A. You’ve just learned how
to find and graph the inverse
sine function and evaluate
related expressions
Now try Exercises 17 through 24
B. The Inverse Cosine and Inverse Tangent Functions
Like the sine function, the cosine function is not one-to-one and its domain must also
be restricted to develop an inverse function. For convenience we choose the interval
since it is again somewhat central and takes on all of its range values in this
interval. A graph of the cosine function, with the interval corresponding to this inter-
val shown in red, is given in Figure 6.10. Note the range is still (Figure 6.11).31, 14
x 30, 4
y cos(x)
x
1
2
3
2
2
2
3
2
y
y cos(x)
x
1
2
3
2
2
y
(, 1)
(0, 1)
y
cos
1
(x)
y cos (x)
x
1
3
2
y
(, 1)
(0, 1)
(1, )
(1, 0)
2
Figure 6.10
Figure 6.11
Figure 6.12
For the implicit equation of inverse cosine, becomes with the
corresponding explicit forms being or By reflecting the
graph of across the line we obtain the graph of shown in
Figure 6.12.
y cos
1
xy x,y cos x
y arccos x.y cos
1
x
x cos y,y cos x
College Algebra & Trignometry—
cob19529_ch06_655-670.qxd 12/26/08 21:08 Page 657

658 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-44
The Inverse Cosine Function
For with domain and range
the inverse cosine function is
or
with domain and range
if and only if
EXAMPLE 4
Evaluating Using Special Values
Evaluate the inverse cosine for the values given:
a. b. c.
Solution
For x in and y in ,
a. y is the number or angle whose cosine is
This shows
b. y is the arc or angle whose cosine is
This shows
c. y is the number or angle whose cosine is
Since is undefined.
Now try Exercises 25 through 34
Knowing that and are inverse functions enables us to state
inverse function properties similar to those for sine.
Inverse Function Properties for Cosine
For and
I. for x in
and
II. for x in
EXAMPLE 5
Evaluating Expressions Using Inverse Function Properties
Evaluate each expression.
a. b. c.
Solution
a. since 0.73 is in Property I
b. since is in Property II30, 4
12
arccosccosa
12
bd
12
,
31, 14cos3cos
1
10.7324 0.73,
cos
1
ccosa
4
3
bdarccosccosa
12
bdcos 3cos
1
10.7324
30, 41g f 21x2 cos
1
1cos x2 x
31, 141f g21x2 cos1cos
1
x2 x
g1x2 cos
1
x:f1x2 cos x
y cos
1
xy cos x
31, 14, cos
1
1 cos y .y cos
1
:
arccosa
13
2
b
5
6
.
13
2
1 cos y
13
2
.
y arccosa
13
2
b:
cos
1
0
2
.
0 1 cos y 0.y cos
1
0:
30, 431, 14
y cos
1
y arccosa
13
2
by cos
1
0
y cos
1
x
cos y xy cos
1
x
30, 4.31, 14
y arccos xy cos
1
x
31, 14,
30, 4y cos x
y
cos
1
(x)
x
1
3
1
2
(1, )
(1, 0)
y
2
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 6:14 PM Page 658 epg HD 049:Desktop Folder:11/11/08:z_old:

6-45 Section 6.5 The Inverse Trig Functions and Their Applications 659
c. since is not in
This expression cannot be evaluated using Property II. Since
The results can also be verified using a calculator.
Now try Exercises 35 through 42
For the tangent function, we likewise restrict the domain to obtain a one-to-one
function, with the most common choice being The corresponding range
is . The implicit equation for the inverse tangent
function is with the explicit forms
or With the domain and
range interchanged, the domain of is
, and the range is The graph of
for x in is shown in red (Figure 6.13), with
the inverse function shown in blue
(Figure 6.14).
The Inverse Tangent Function Inverse Function Properties for Tangent
For with domain and For and
range , the inverse tangent function is I. for x in
or
and
with domain and range II. for x in
if and only if
EXAMPLE 6
Evaluating Expressions Involving Inverse Tangent
Evaluate each expression.
a. b.
Solution
For x in and y in
a. since
b. since is in Property II
Now try Exercises 43 through 52
a
2
,
2
b0.89arctan3tan10.89240.89,
tana
3
b13tan
1
1132
3
,
a
2
,
2
b,
arctan3tan 10.8924tan
1
1132
tan y xy tan
1
x
a
2
,
2
b.1g f 21x2 tan
1
1tan x2 xa
2
,
2
b.
y arctan x,tan
1
xy
1f g21x2 tan1tan
1
x2 x
g1x2 tan
1
x:f 1x2 tan xa
2
,
2
by tan x
y tan
1
x
a
2
,
2
b
y tan xa
2
,
2
b.
y tan
1
x
y arctan x.y tan
1
x
x tan y
a
2
,
2
b.
cosa
4
3
b cosa
2
3
b, cos
1
ccosa
4
3
bd cos
1
ccosa
2
3
bd
2
3
.
30, 4.
4
3
cos
1
ccosa
4
3
bd
4
3
,
y tan x
x
y
3
1
2
3
1
2
, 1
4
, 1
4
y tan
1
x
4
1,
4
1,
2
2
x
y
3
1
2
3
1
2
Figure 6.13
Figure 6.14
B. You’ve just learned
how to find and graph the
inverse cosine and tangent
functions and evaluate related
expressions
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 6:14 PM Page 659 epg HD 049:Desktop Folder:11/11/08:z_old:
