Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.

660 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-46
C. Using the Inverse Trig Functions to Evaluate Compositions
In the context of angle measure, the expression represents an angle—
the angle y whose sine is It seems natural to ask, “What happens if we take the
tangent of this angle?” In other words, what does the expression
mean? Similarly, if represents a real number between and 1, how do
we compute ? Expressions like these occur in many fields of study.
EXAMPLE 7
Simplifying Expressions Involving Inverse Trig Functions
Simplify each expression:
a. b.
Solution
a. In Example 1 we found Substituting for
gives showing
b. For we begin with the inner function
Substituting for gives With the appropriate checks
satisfied we have showing
Now try Exercises 53 through 64
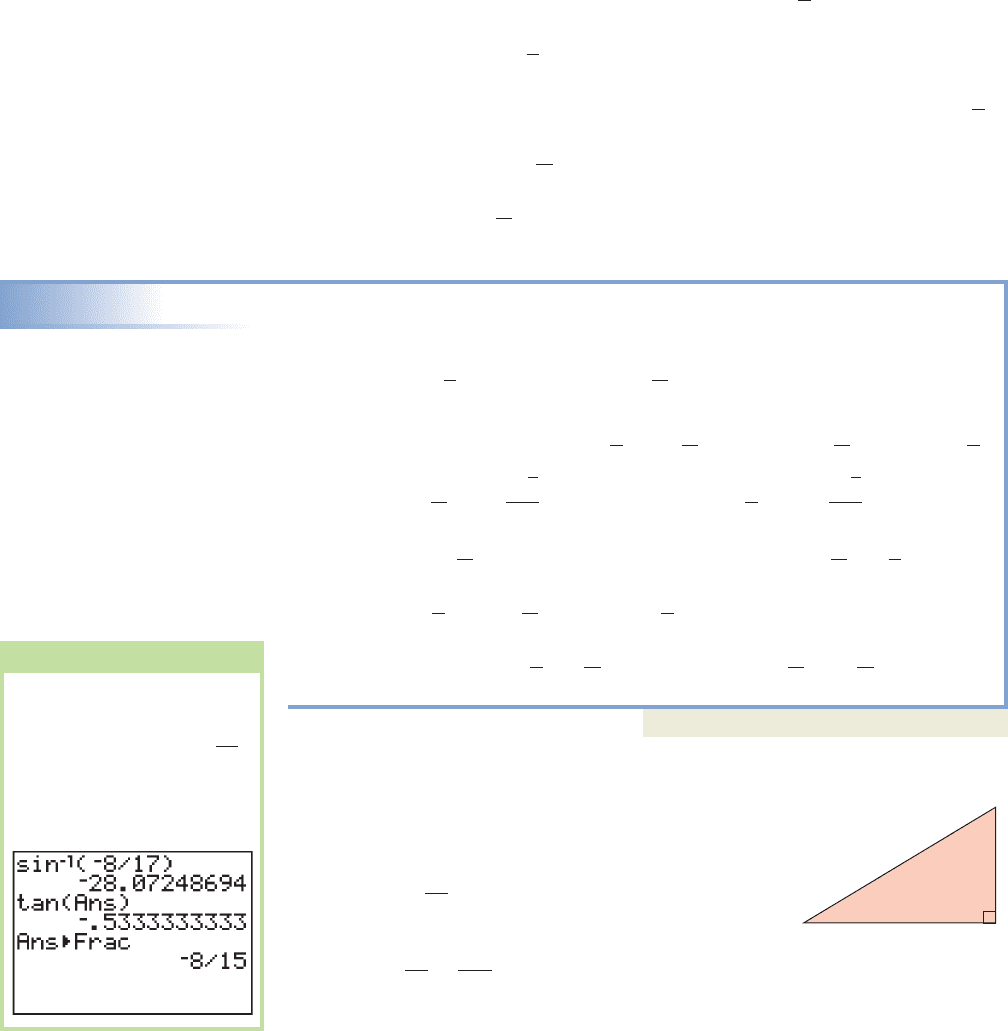
If the argument is not a special value and we need the
answer in exact form, we can draw the triangle described
by the inner expression using the definition of the trigono-
metric functions as ratios. In other words, for either
y or we draw a triangle with hypotenuse
17 and side 8 opposite to model the statement, “an angle
whose sine is ” (see Figure 6.15). Using the Pythagorean theorem, we find
the adjacent side is 15 and can now name any of the other trig functions.
8
17
opp
hyp
sin
1
a
8
17
b,
sin
1
ccosa
3
bd
6
.sin
1
a
1
2
b
6
,
sin
1
a
1
2
b.cosa
3
b
1
2
cosa
3
b
1
2
.sin
1
ccosa
3
bd,
tancarcsina
1
2
bd
13
3
.tana
6
b
13
3
,
arcsina
1
2
b
6
arcsina
1
2
b
6
.
sin
1
ccosa
3
bdtancarcsina
1
2
bd
sin
1
ccosa
3
bd
1y cosa
3
b
tancsin
1
a
1
2
bd
1
2
.
y sin
1
a
1
2
b
17
adj
8
Figure 6.15
WORTHY OF NOTE
To verify the result of
Example 8, we can actually
find the value of
on a calculator, then take the
tangent of the result. See the
figure.
sin
1
a
8
17
b
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 6:14 PM Page 660 epg HD 049:Desktop Folder:11/11/08:z_old:
6-47 Section 6.5 The Inverse Trig Functions and Their Applications 661
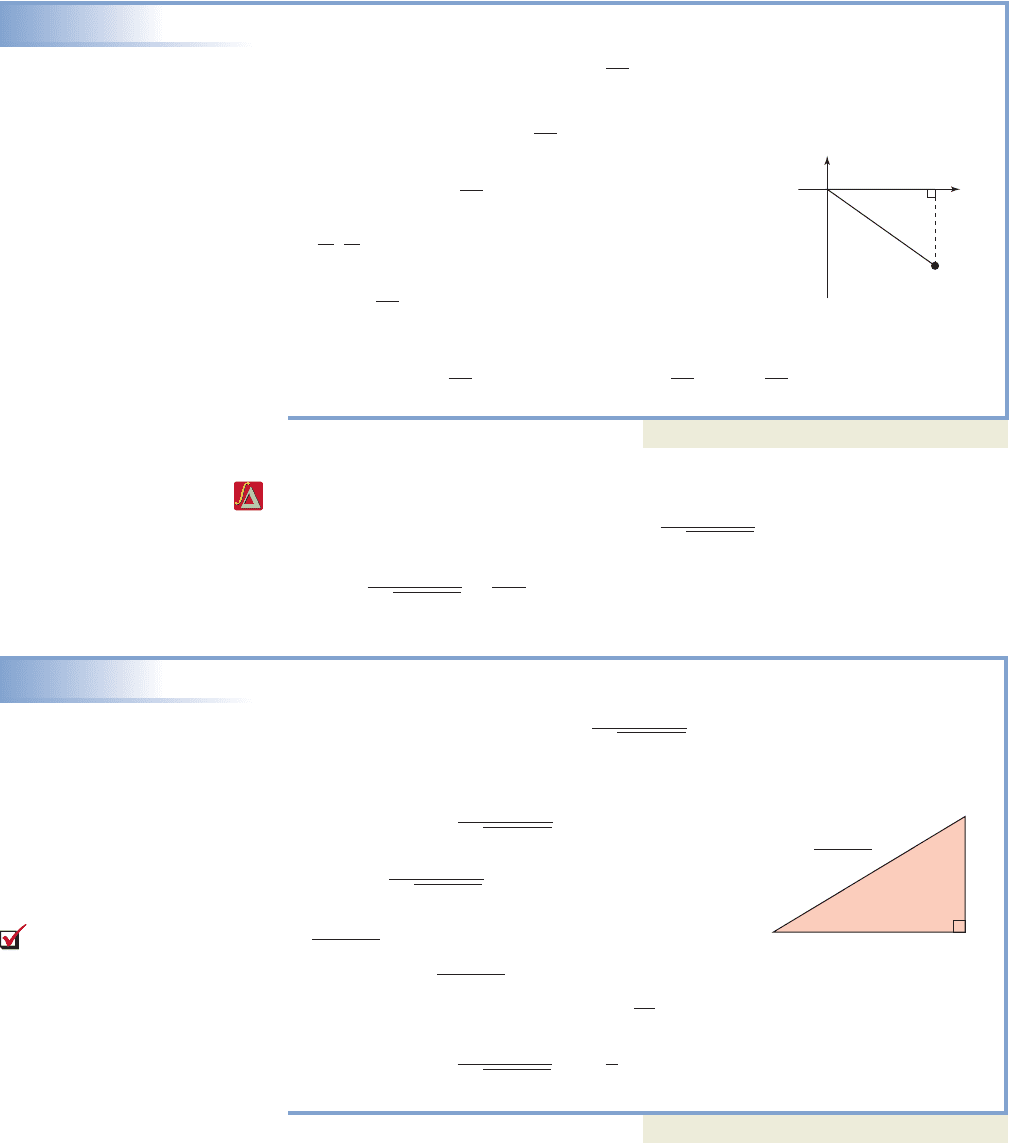
EXAMPLE 8
Using a Diagram to Evaluate an Expression Involving Inverse Trig Functions
Evaluate the expression
Solution
The expression is equivalent to
where with in
(QIV or QI). For
must be in
QIII or QIV. To satisfy both, must be in QIV. From the figure
we note showing
Now try Exercises 65 through 72
These ideas apply even when one side of the triangle is unknown. In other words,
we can still draw a triangle for since “ is an angle whose
cosine is ”
EXAMPLE 9
Using a Diagram to Evaluate an Expression Involving Inverse Trig Functions
Evaluate the expression Assume and the inverse
function is defined for the expression given.
Solution
Rewrite as where
Draw a triangle with
side x adjacent to and a hypotenuse of
The Pythagorean theorem gives
which leads to
giving This shows
(see the figure).
Now try Exercises 73 through 76
D. The Inverse Functions for Secant, Cosecant, and Cotangent
As with the other functions, we restrict the domain of the secant, cosecant, and cotangent
functions to obtain a one-to-one function that is invertible (an inverse can be found).
Once again the choice is arbitrary, and some domains are easier to work with than
others in more advanced mathematics. For we’ve chosen the “mosty sec x,
tan tanccos
1
a
x
2x
2
16
bd
4
x
opp 116
4.opp
2
1x
2
162 x
2
x
2
opp
2
12x
2
162
2
,
2x
2
16.
cos
1
a
x
2x
2
16
b.
tan ,tanccos
1
a
x
2x
2
16
bd
x 7 0tanccos
1
a
x
2x
2
16
bd.
x
2x
2
16
adj
hyp
.
cos
1
a
x
2x
2
16
b,
tancsin
1
a
8
17
bd
8
15
.tan
8
15
,
sin
8
17
1sin 6 02,
c
2
,
2
d
sin
1
a
8
17
b
tan ,tancsin
1
a
8
17
bd
tancsin
1
a
8
17
bd.
15
17
(15, 8)
8
x
opp
√x
2
16
C. You’ve just learned
how to apply the definition
and notation of inverse trig
functions to simplify
compositions
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 6:14 PM Page 661 epg HD 049:Desktop Folder:11/11/08:z_old:
662 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-48
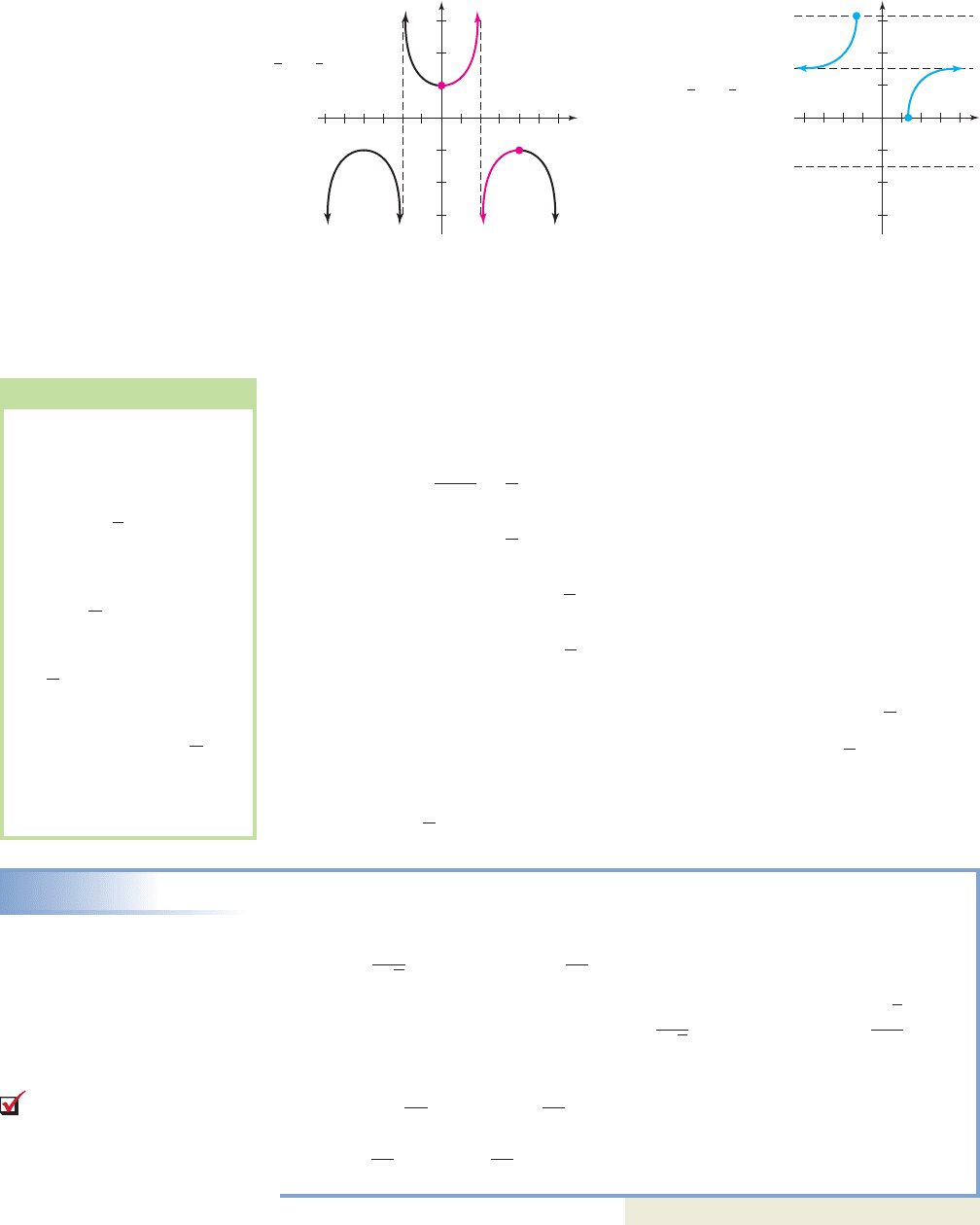
intuitive” restriction, one that seems more centrally located (nearer the origin). The
graph of is reproduced here, along with its inverse function (see Figures 6.16
and 6.17). The domain, range, and graphs of the functions and
are asked for in the Exercises (see Exercise 100).
The functions , and can be evaluated by
noting their relationship to , and , respectively. For
, we have
definition of inverse function
property of reciprocals
reciprocal ratio
rewrite using inverse function notation
substitute for y
In other words, to find the value of evaluate .
Similarly, the expression can be evaluated using . The
expression can likewise be evaluated using an inverse tangent function:
EXAMPLE 10
Evaluating an Inverse Trig Function
Evaluate using a calculator only if necessary:
a. b.
Solution
a. From our previous discussion, for we evaluate
Since this is a standard value, no calculator is needed and the result is
b. For find on a calculator:
Now try Exercises 77 through 86
tan
1
a
12
b 1.3147.cot
1
a
12
b
tan
1
a
12
bcot
1
a
12
b,
30°.
cos
1
a
13
2
b.sec
1
a
2
13
b,
cot
1
a
12
bsec
1
a
2
13
b
tan
1
a
1
x
b.cot
1
x
cot
1
x
sin
1
a
1
x
b,
x
1csc
1
x
y cos
1
a
1
x
b,
x
1y sec
1
x,
sec
1
x sec
1
x cos
1
a
1
x
b
y cos
1
a
1
x
b
cos y
1
x
1
sec y
1
x
sec y x
y sec
1
x
y tan
1
xy cos
1
x, y sin
1
x
y cot
1
xy sec
1
x, y csc
1
x
y cot
1
xy csc
1
x
y sec x
x
y
3
1
2
3
1
2
x [0, ) ( , ]
2
2
y sec x
y
(, 1] [1, )
x
y
3
1
2
3
1
2
y sec
1
x
x
(, 1] [1, )
y [0, ) ( ,
]
2
2
Figure 6.16
y sec x
Figure 6.17
y sec
1
x
WORTHY OF NOTE
While the domains of
and
both include all real
numbers, evaluating
using involves the
restriction To maintain
consistency, the equation
is often
used. The graph of
is that of
reflected across
the x-axis and shifted
units up, with the result
identical to the graph of
.y cot
1
x
2
y tan
1
x
y
2
tan
1
x
cot
1
x
2
tan
1
x
x 0.
tan
1
a
1
x
b
cot
1
x
y tan
1
xy cot
1
x
D. You’ve just learned
how to find and graph inverse
functions for sec x, csc x, and
cot x
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 6:14 PM Page 662 epg HD 049:Desktop Folder:11/11/08:z_old:
6-49 Section 6.5 The Inverse Trig Functions and Their Applications 663
A summary of the highlights from this section follows.
Summary of Inverse Function Properties and Compositions
1. For sin x and 2. For cos x and
for any x in the interval for any x in the interval
for any x in the interval
for any x in the interval
E. Applications of Inverse Trig Functions
We close this section with one example of the many ways that inverse functions can
be applied.
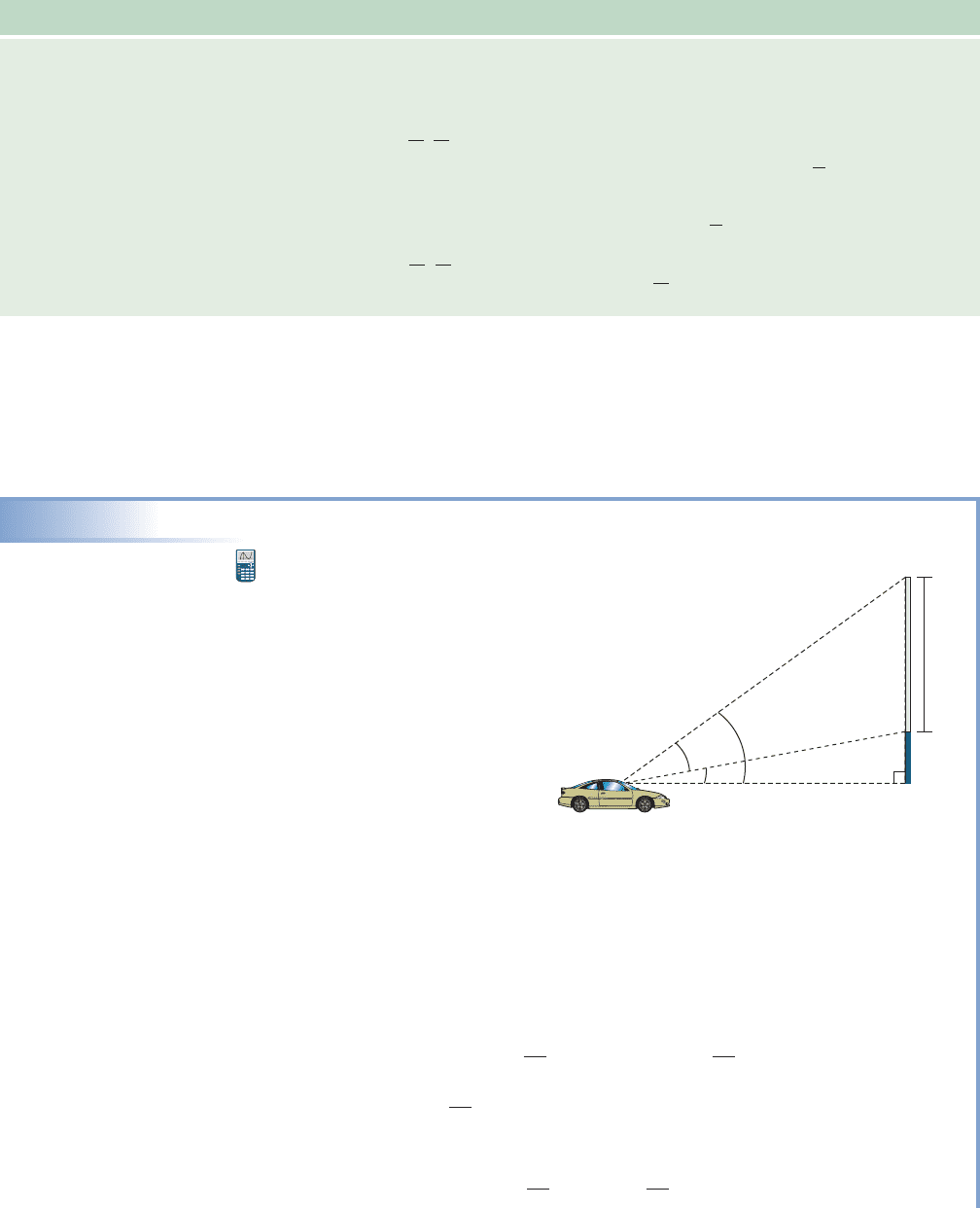
EXAMPLE 11
Using Inverse Trig Functions to Find Viewing Angles
Believe it or not, the drive-in
movie theaters that were so
popular in the 1950s are
making a comeback! If you
arrive early, you can park in
one of the coveted “center
spots,” but if you arrive late,
you might have to park very
close and strain your neck to
watch the movie. Surprisingly,
the maximum viewing angle
(not the most comfortable
viewing angle in this case) is actually very close to the front. Assume the base of a
30-ft screen is 10 ft above eye level (see Figure 6.18).
a. Use the inverse function concept to find expressions for angle and angle .
b. Use the result of Part (a) to find an expression for the viewing angle .
c. Use a calculator to find the viewing angle (to tenths of a degree) for
distances of 15, 25, 35, and 45 ft, then to determine the distance x (to tenths of
a foot) that maximizes the viewing angle.
Solution
a. The side opposite is 10 ft, and we want to know x — the adjacent side. This
suggests we use giving In the same way, we find
that
b. From the diagram we note that and substituting for and
directly gives tan
1
a
40
x
b tan
1
a
10
x
b.
,
tan
1
a
40
x
b.
tan
1
a
10
x
b.tan
10
x
,
30, 4cos
1
1cos x2 x,
c
2
,
2
dsin
1
1sin x2 x,
31, 14cos1cos
1
x2 x,31, 14sin1sin
1
x2 x,
cos
1
x,sin
1
x,
Figure 6.18
x
10 ft
30 f
t
College Algebra & Trignometry—
4. To evaluate use
use
use for all real numbers x
2
tan
1
x,cot
1
x,
sin
1
a
1
x
b,
x
1csc
1
x,
cos
1
a
1
x
b,
x
1,
sec
1
x,
3. For tan x and
for any real number x
for any x in the interval a
2
,
2
btan
1
1tan x2 x,
tan1tan
1
x2 x,
tan
1
x,
cob19529_ch06_615-700.qxd 11/11/08 6:14 PM Page 663 epg HD 049:Desktop Folder:11/11/08:z_old:

c. After we enter a graphing calculator gives
approximate viewing angles of
and for
25, 35, and 45 ft, respectively. From these
data, we note the distance x that makes a
maximum must be between 15 and 35 ft,
and using (CALC)
4:maximum shows is a maximum of
at a distance of 20 ft from the screen
(see Figure 6.19).
Now try Exercises 89 through 95
36.9°
TRACE
2nd
x 15,29.1°,35.8 °, 36.2°, 32.9°,
Y
1
tan
1
a
40
x
b tan
1
a
10
x
b,
664 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-50
E. You’ve just learned
how to solve applications
involving inverse functions
Figure 6.19
0 100
50
0
More on Inverse Functions
TECHNOLOGY HIGHLIGHT
The domain and range of the inverse functions for sine, cosine, and
tangent are preprogrammed into most graphing calculators, making
them an ideal tool for reinforcing the concepts involved. In particular,
implies that only if and
For a stark reminder of this fact we’ll use the TABLE
feature of the grapher. Begin by using the TBLSET screen (
) to set TblStart with After placing the
calculator in degree , go to the screen and input
and (the composition ).
Then disable Y
2
[turn it off—Y
3
will read it anyway) so that both Y
1
and
Y
3
will be displayed simultaneously on the TABLE screen. Pressing
brings up the TABLE shown in Figure 6.20, where we
note the inputs are standard angles, the outputs in Y
1
are the
(expected) standard values, and the outputs in Y
3
return the original
standard values. Now scroll upward until is at the top of the
X column (Figure 6.21), and note that Y
3
continues to return standard
angles from the interval —a stark reminder that while the
expression Once again we note that while can be
evaluated, it cannot be evaluated directly using the inverse function properties. Use these ideas to
complete the following exercises.
Exercise 1: Go through an exercise similar to the one here using and Remem-
ber to modify the TBLSET to accommodate the restricted domain for cosine.
Exercise 2: Complete parts (a) and (b) using the TABLE from Exercise 1. Complete parts (c) and (d)
without a calculator.
a. b.
c. d.
cos
1
1cos 240°2cos
1
1cos 120°2
cos
1
1cos 210°2cos
1
1cos 150°2
Y
2
cos
1
x.Y
1
cos x
sin
1
1sin 150°2sin 150° 0.5, sin
1
1sin 150°2 150°.
390°, 90°4
180°
GRAPH
2nd
Y
2
Y
1
Y
3
Y
2
1Y
1
2Y
1
sin x, Y
2
sin
1
x,
Y =MODE
¢Tbl 30. 90
WINDOW
2nd
1 x 1.
90° y 90°sin
1
y xsin x y
Figure 6.20
Figure 6.21
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 6:14 PM Page 664 epg HD 049:Desktop Folder:11/11/08:z_old:
6-51 Section 6.5 The Inverse Trig Functions and Their Applications 665
DEVELOPING YOUR SKILLS
The tables here show values of ,
,
and for
[
to
]. The restricted domain used to
develop the inverse functions is shaded. Use the
210180
tan cos sin
CONCEPTS AND VOCABULARY
Fill in each blank with the appropriate word or phrase.
Carefully reread the section if needed.
1. All six trigonometric functions fail the
test and therefore are not
to .
2. The two most common ways of writing the inverse
function for are and .
3. The domain for the inverse sine function is
and the range is .
y sin x
4. The domain for the inverse cosine function is
and the range is .
5. Most calculators do not have a key for evaluating
an expression like Explain how it is done
using the key.
6. Discuss/Explain what is meant by the implicit form
of an inverse function and the explicit form. Give
algebraic and trigonometric examples.
sec
1
5.
y sin
y cos y tan
0
0
01
13
2
210°
1180°
13
2
30°
13
2
150°
1
2
60°
1
2
120°90°
90°
1
2
120°
1
2
60°
13
2
150°
13
2
30°1180°
cos cos
Use the preceding tables to fill in each blank (principal values only).
sin
1
112sina
2
b1
sin
1
a
1
2
bsina
5
6
b
1
2
arcsina
1
2
b
6
sina
6
b
sin
1
0 sin 0 0
arcsin 0 0sin 180°
arcsina
13
2
bsin160°2
13
2
sin
1
a
13
2
bsin 120°
13
2
sin
1
0 sin 0
0
1
0
00
1
2
210°
180°
1
2
30°
1
2
150°
13
2
60°
13
2
120°190°
90°
13
2
120°
13
2
60°
1
2
150°
1
2
30°180°
sin sin
6.5 EXERCISES
information from these tables to complete the exercises
that follow.
7. 8.
0
—
—
0
00 13
210°
180°
13
3
30°
13
3
150°1360°
13
120°90°
90°13
120°
13
60°
13
3
150°
13
3
30°180°
tan tan
College Algebra & Trignometry—
cob19529_ch06_655-670.qxd 12/29/2008 09:19 am Page 665
Evaluate without the aid of calculators or tables,
keeping the domain and range of each function in mind.
Answer in radians.
9. 10.
11. 12.
Evaluate using a calculator, keeping the domain and
range of each function in mind.Answer in radians to the
nearest ten-thousandth and in degrees to the nearest
tenth.
13. arcsin 0.8892 14.
15. 16.
Evaluate each expression.
17. 18.
19. 20.
21. 22.
23. 24.
Use the tables given prior to Exercise 7 to fill in each
blank (principal values only).
25.
26.
sincarcsina
3
5
bdsin 1sin
1
0.82052
arcsincsina
2
3
bdsin
1
1sin 135°2
sin
1
1sin 30°2arcsincsina
3
bd
sincarcsina
13
2
bdsincsin
1
a
12
2
bd
sin
1
a
1 15
2
bsin
1
a
1
17
b
arcsina
7
8
b
arcsina
1
2
bsin
1
1
arcsina
13
2
bsin
1
a
12
2
b
Evaluate without the aid of calculators or tables.
Answer in radians.
27. 28.
29. 30. arccos (0)
Evaluate using a calculator. Answer in radians to the
nearest ten-thousandth, degrees to the nearest tenth.
31. arccos 0.1352 32.
33. 34.
Evaluate each expression.
35. 36.
37. 38.
39. 40.
41. 42.
Use the tables presented before Exercise 7 to fill in each
blank. Convert from radians to degrees as needed.
43.
44.
Evaluate without the aid of calculators or tables.
45. 46.
47. 48. tan
1
0arctan1132
arctan112tan
1
a
13
3
b
arccos1cos 44.2°2cos
1
ccosa
5
4
bd
coscarccosa
13
2
bdcosccos
1
a
12
2
bd
coscarccos a
8
17
bdcos1cos
1
0.55602
cos
1
1cos 60°2arccosccosa
4
bd
cos
1
a
16 1
5
bcos
1
a
15
3
b
arccosa
4
7
b
cos
1
112
arccosa
13
2
bcos
1
a
1
2
b
666 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-52
cos
1
112cos 1
arccosa
1
2
bcos 120°
1
2
arccosa
13
2
b
6
cosa
6
b
cos
1
1 cos 0 1
tan
1
1132tana
3
b
arctana
13
3
btan 30°
13
3
arctan113
2
3
tana
3
b
tan
1
0 tan 0 0
arctan 1
4
tana
4
b
arctan 1132tan 120° 13
tan
1
0 tan 0
tan
1
a
13
3
btan1150°2
13
3
cos
1
1 cos122 1
arccosa
1
2
b 120°cos1120°2
cos
1
a
13
2
bcosa
6
b
13
2
cos
1
a
1
2
bcos160°2
1
2
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 6:14 PM Page 666 epg HD 049:Desktop Folder:11/11/08:z_old:

Evaluate using a calculator, keeping the domain and
range of each function in mind.Answer in radians to the
nearest ten-thousandth and in degrees to the nearest
tenth.
49. 50.
51. 52.
Simplify each expression without using a calculator.
53. 54.
55. 56.
57. 58.
59. 60.
Explain why the following expressions are not defined.
61. 62. cot(arccos 1)
63. 64.
Use the diagrams below to write the value of: (a) ,
(b) , and (c) .
65. 66.
67. 68.
10
3x
√100 9x
2
6
x
√x
2
36
10
20
10√3
0.3
0.5
0.4
tan cos
sin
cos
1
cseca
2
3
bdsin
1
ccsca
4
bd
tan1sin
1
12
arcsin1cos 135°2arccos3sin130°24
cotccos
1
a
1
2
bdcsccsin
1
a
12
2
bd
seccarcsina
1
2
bdtancarccosa
13
2
bd
cos
1
csina
3
bdsin
1
ccosa
2
3
bd
arctan1162arctana
29
21
b
tan
1
10.32672tan
1
12.052
Evaluate each expression by drawing a right triangle
and labeling the sides.
69. 70.
71. 72.
73. 74.
75.
76.
Use the tables given prior to Exercise 7 to help fill in
each blank.
77.
78.
Evaluate using a calculator only as necessary.
79. arccsc 2 80.
81. 82.
83. arcsec 5.789 84.
85. 86. arccsc 2.9875sec
1
17
cot
1
a
17
2
b
arccot112cot
1
13
csc
1
a
2
13
b
tancsec
1
a
29 x
2
x
bd
coscsin
1
a
x
212 x
2
bd
tancarcseca
5
2x
bdcotcarcsina
3x
5
bd
tanccos
1
a
123
12
bdsinctan
1
a
15
2
bd
coscsin
1
a
11
61
bdsinccos
1
a
7
25
bd
6-53 Section 6.5 The Inverse Trig Functions and Their Applications 667
sec
1
2 60°sec160°2
arcsec 1 sec1360°2 1
arcseca
2
13
bseca
7
6
b
2
13
arcsec 2 sec160°2 2
WORKING WITH FORMULAS
87. The force normal to an object on an inclined
plane:
When an object is on an inclined plane, the normal
force is the force acting perpendicular to the plane
and away from the force of gravity, and is
measured in a unit called newtons (N). The
magnitude of this force depends on the angle of
incline of the plane according to the formula
F
N
mg cos
above, where m is the mass of the object in
kilograms and g is the force of gravity (9.8 m/sec
2
).
Given , find (a) F
N
for and
and (b) for and .F
N
2 NF
N
1 N 45°
15°m 225 g
g
F
N
225 kg
225 kg
g
F
N
College Algebra & Trignometry—
sec
1
112
sec12
arcseca
2
13
bsec130°2
2
13
arcsec 2
3
seca
3
b
sec
1
1 sec 0 1
cob19529_ch06_655-670.qxd 12/29/08 19:54 Page 667

When a circular pipe is
exposed to a fan-driven
source of heat, the
temperature of the air
reaching the pipe is
greatest at the point
nearest to the source
(see diagram). As you
move around the
circumference of the
pipe away from the
source, the temperature
of the air reaching the
pipe gradually
decreases.
One possible model of this phenomenon is given by
the formula shown, where T is the temperature of
the air at a point (x, y) on the circumference of a
pipe with outer radius , T
0
is the
temperature of the air at the source, and T
R
is the
surrounding room temperature. Assuming
, and : (a) Find the
temperature of the air at the points (0, 5), (3, 4), (4,
3), (4.58, 2), and (4.9, 1).
(b) Why is the temperature decreasing for this
sequence of points? (c) Simplify the formula using
and use it to find two points on the pipe’s
circumference where the temperature of the air
is .
113°
r 5
r 5 cmT
R
72°T
0
220°F
r 2x
2
y
2
668 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-54
y
x
2
y
2
r
2
Pipe
Heat source
Fan
x
r
APPLICATIONS
89. Snowcone
dimensions: Made in
the Shade Snowcones
sells a colossal size
cone that uses a conical
cup holding 20 oz of
ice and liquid. The cup
is 20 cm tall and has a
radius of 5.35 cm. Find
the angle formed by a
cross-section of the cup.
90. Avalanche conditions: Winter avalanches occur
for many reasons, one being the slope of the
mountain. Avalanches
seem to occur most often
for slopes between
and (snow gradually
slides off steeper
slopes). The slopes at a
local ski resort have an
average rise of 2000 ft
for each horizontal run
of 2559 ft. Is this resort
prone to avalanches?
Find the angle and
respond.
60°
35°
91. Distance to hole: A
popular story on the
PGA Tour has Gerry Yang, Tiger
Woods’teammate at Stanford
and occasional caddie, using
the Pythagorean theorem to
find the distance Tiger
needed to reach a
particular hole. Suppose
you notice a marker in
the ground stating that
the straight line
distance from the
marker to the hole (H)
is 150 yd. If your ball B
is 48 yd from the marker (M) and angle BMH is a
right angle, determine the angle and your straight
line distance from the hole.
92. Ski jumps: At a
waterskiing contest on
a large lake, skiers use
a ramp rising out of the
water that is 30 ft long
and 10 ft high at the
high end. What angle
does the ramp make
with the lake?
2000 ft
2559 ft
30 ft
10 ft
150 yd
48 yd
Marker
M
B
H
20 cm
5.35 cm
College Algebra & Trignometry—
Exercise 89
Exercise 90
Exercise 91
Exercise 92
88. Heat flow on a cylindrical pipe:
T 1T
0
T
R
2 sina
y
2x
2
y
2
b T
R
; y 0
cob19529_ch06_655-670.qxd 12/26/08 21:14 Page 668
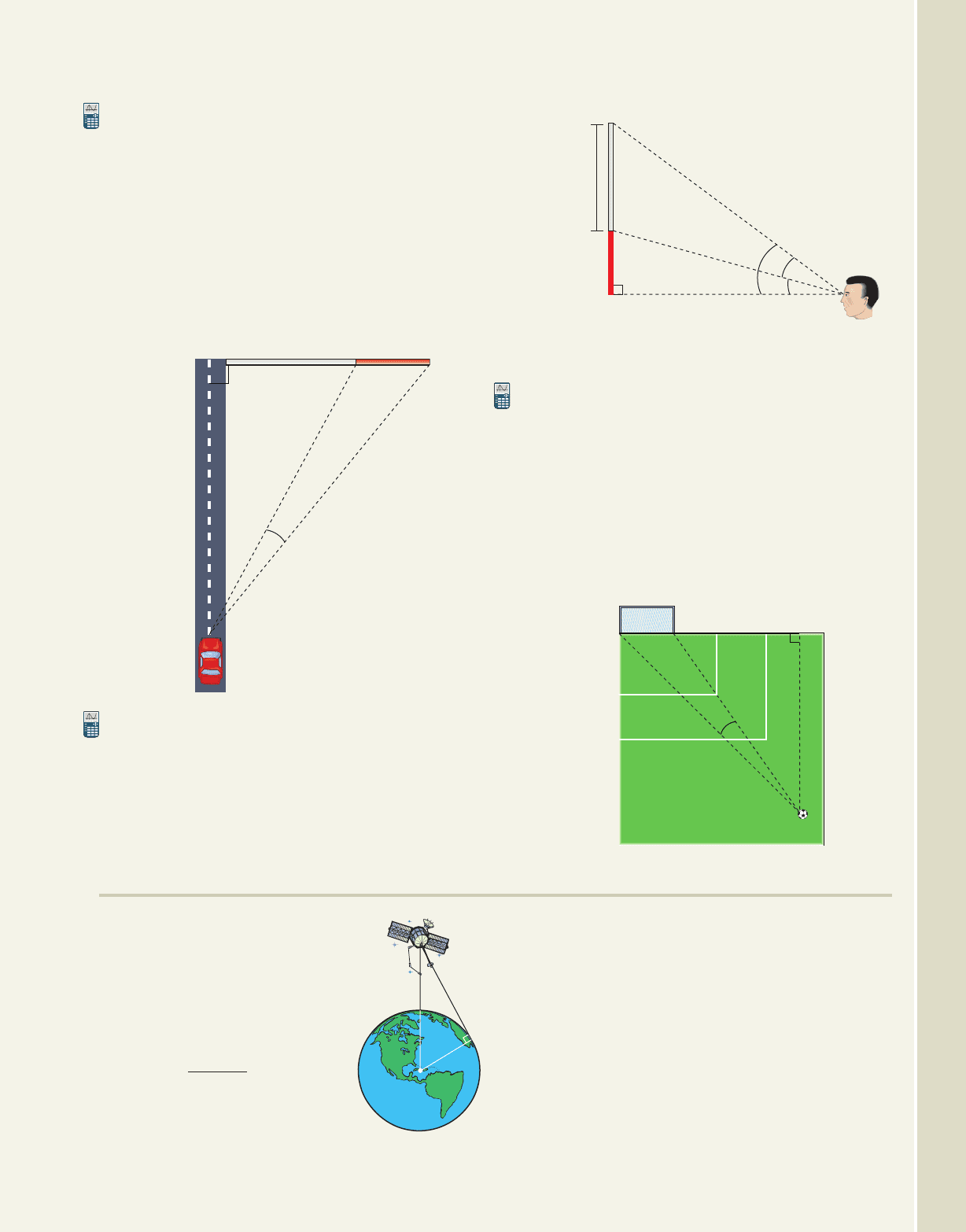
6-55 Section 6.5 The Inverse Trig Functions and Their Applications 669
Exercise 94
Exercise 95
x
2.5 ft
1.5 ft
Exercise 93
d
25 ft
50 ft
d
70 ft
(goal area)
(penalty area)
(sideline)
24 ft
93. Viewing angles for advertising: A 25-ft-wide
billboard is erected perpendicular to a straight
highway, with the closer edge 50 ft away (see
figure). Assume the advertisement on the billboard
is most easily read when the viewing angle is
or more. (a) Use inverse functions to find an
expression for the viewing angle . (b) Use a
calculator to help determine the distance d (to
tenths of a foot) for which the viewing angle is
greater than . (c) What distance d maximizes
this viewing angle?
10.5°
10.5°
EXTENDING THE CONCEPT
Consider a satellite orbiting at an
altitude of x mi above the Earth.
The distance d from the satellite
to the horizon and the length s of
the corresponding arc of the
Earth are shown in the diagram.
96. To find the distance d we
use the formula
(a) Show
how this formula was
developed using the
d 22rx x
2
.
Pythagorean theorem. (b) Find a formula for the
angle in terms of r and x, then a formula for the
arc length s.
97. If the Earth has a radius of 3960 mi and the
satellite is orbiting at an altitude of
150 mi, (a) what is the measure of angle ?
(b) how much longer is d than s?
Earth
r
r
Center
of the Earth
s
x
d
College Algebra & Trignometry—
calculator to help determine the distance x (to tenths
of a foot) that maximizes this viewing angle.
95. Shooting angles and shots on goal: A soccer
player is on a breakaway and is dribbling just
inside the right sideline toward the opposing goal
(see figure). As the defense closes in, she has just a
few seconds to decide when to shoot. (a) Use
inverse functions to find an expression for the
shooting angle . (b) Use a calculator to help
determine the distance d (to tenths of a foot) that
will maximize the shooting angle for the
dimensions shown.
94. Viewing angles at an art show: At an art show, a
painting 2.5 ft in height is hung on a wall so that its
base is 1.5 ft above the eye level of an average
viewer (see figure). (a) Use inverse functions to find
expressions for angles and . (b) Use the result to
find an expression for the viewing angle . (c) Use a
cob19529_ch06_615-700.qxd 11/11/08 6:14 PM Page 669 epg HD 049:Desktop Folder:11/11/08:z_old:
