Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.


610 CHAPTER 5 An Introduction to Trigonometry 5-108
7. Given and find the value of the
other five trig functions of
8. Verify that is a point on the unit circle,
then find the value of all six trig functions associated
with this point.
9. In order to take pictures of a dance troupe as it
performs, a camera crew rides in a cart on tracks that
trace a circular arc. The radius of the arc is 75 ft, and
from end to end the cart sweeps out an angle of
in 20 seconds. Use this information to find
(a) the length of the track in feet and inches, (b) the
angular velocity of the cart, and (c) the linear
velocity of the cart in both ft/sec and mph.
172.5°
a
1
3
,
212
3
b
.
tan 6 0,cos
2
5
College Algebra & Trignometry—
10. Solve the triangle shown.
Answer in table form.
11. The “plow” is a yoga position
in which a person lying on
their back brings their feet
up, over, and behind their
head and touches them to the
floor. If distance from hip to shoulder (at the right
angle) is 57 cm and from hip to toes is 88 cm, find
the distance from shoulders to toes and the angle
formed at the hips.
12. While doing some
night fishing, you
round a peninsula
and a tall light house
comes into view.
Taking a sighting,
you find the angle of
elevation to the top
of the lighthouse is
If the lighthouse
is known to be 27 m tall, how far from the
lighthouse are you?
13. Find the value of satisfying the
conditions given.
a. t in QIII
b. t in QIV
c. t in QIItan t 1,
sec t
213
3
,
sin t
1
2
,
t 30, 24
25°.
A
rms
T
o
r
so
Legs
Hi
ps
H
ea
d
T
oes
15.0 cm
AC
B
57
Exercise 10
Exercise 11
14. In arid communities, daily water usage can often be
approximated using a sinusoidal model. Suppose
water consumption in the city of Caliente del Sol
reaches a maximum of 525,000 gallons in the heat of
the day, with a minimum usage of 157,000 gallons
in the cool of the night. Assume corresponds
to 6:00 A.M. (a) Use the information to construct a
sinusoidal model, and (b) Use the model to
approximate water usage at 4:00 P.M. and 4:00 A.M.
15. State the domain, range, period, and amplitude (if it
exists), then graph the function over 1 period.
a. b.
c.
16. State the amplitude, period, horizontal shift, vertical
shift, and endpoints of the primary interval. Then
sketch the graph using a reference rectangle and the
rule of fourths:
17. An athlete throwing the shot-put begins his first
attempt facing due east, completes three and one-
half turns and launches the shot facing due west.
What angle did his body turn through?
18. State the domain, range, and period, then sketch the
graph in
a. b.
19. Due to tidal motions,
the depth of water in
Brentwood Bay varies
sinusoidally as shown in the
diagram, where time is in
hours and depth is in feet.
Find an equation that models
the depth of water at time t.
20. Find the value of t satisfying
the given conditions.
a. t in QIII
b. t in QII
sec t 1.5;
sin t 0.7568;
y cota
1
2
tby tan12t2
30, 22.
y 12 sina3t
4
b 19.
y 2 tan13t2
y sec ty 2 sina
5
tb
t 0
25
27 m
Exercise 12
Time (hours)
Depth (ft)
20 241612840
8
4
16
20
12
Exercise 19
cob19529_ch05_601-614.qxd 01/13/2009 09:12 PM Page 610 ssen 1 HD 049:Desktop Folder:Satya 13/01/09:Used file:MHDQ092-5-SUMM:
5-109 Calculator Exploration and Discovery 611
Variable Amplitudes
and Modeling the
Tides
Tidal motion is often too complex to be modeled by a single sine function. In this
Exploration and Discovery, we’ll look at a method that combines two sine functions
to help model a tidal motion with variable amplitude. In the process, we’ll use much
of what we know about the amplitude, horizontal shifts and vertical shifts of a sine
function, helping to reinforce these important concepts and broaden our understand-
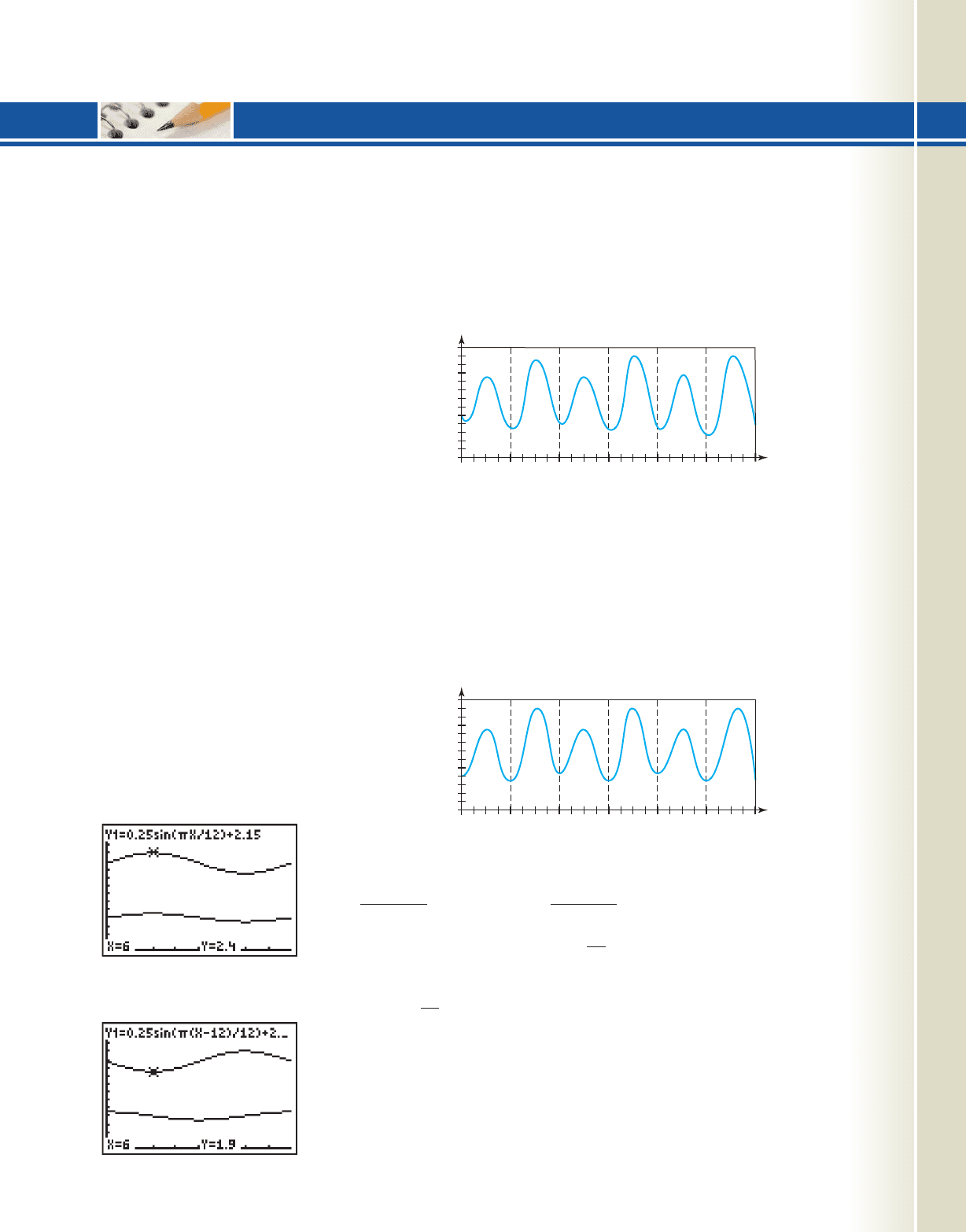
ing about how they can be applied. The graph in Figure 5.93 shows three days of tidal
motion for Davis Inlet, Canada.
As you can see, the amplitude of the graph varies, and there is no single sine func-
tion that can serve as a model. However, notice that the amplitude varies predictably,
and that the high tides and low tides can independently be modeled by a sine function.
To simplify our exploration, we will use the assumption that tides have an exact 24-hr
period (close, but no), that variations between high and low tides takes place every 12 hr
(again close but not exactly true), and the variation between the “low-high” (1.9 m) and
the “high-high” (2.4 m) is uniform. A similar assumption is made for the low tides. The
result is the graph in Figure 5.94.
First consider the high tides, which vary from a maximum of 2.4 to a minimum of
1.9. Using the ideas from Section 5.7 to construct an equation model gives
and With a period of hr we
obtain the equation Using 0.9 and 0.7 as the
maximum and minimum low tides, similar calculations yield the equation
(verify this). Graphing these two functions over a 24-hr period
yields the graph in Figure 5.95, where we note the high and low values are correct, but the
two functions are in phase with each other. As can be determined from Figure 5.94, we
want the high tide model to start at the average value and decrease, and the low tide equa-
tion model to start at high-low and decrease. Replacing x with in Y
1
and x with
in Y
2
accomplishes this result (see Figure 5.96). Now comes the fun part! Since Y
1
x 6
x 12
Y
2
0.1 sina
12
xb 0.8
Y
1
0.25 sina
12
xb 2.15.
P 24D
2.4 1.9
2
2.15.A
2.4 1.9
2
0.25
0.9
0.7
0.9
0.7
0.9
0.7
2.4
2.4
1.9
1.9 1.9
2.4
t
Height (m)
0
1
2
Midni
g
ht Noon Midni
g
ht Noon Midni
g
ht Noon Midni
g
h
t
0.9
0.7
0.8
0.7
0.7
0.6
2.42.4
2.0
1.9 1.9
2.3
t
Height (m)
0
1
2
Midni
g
ht Noon Midni
g
ht Noon Midni
g
ht Noon Midni
g
h
t
College Algebra & Trignometry—
Figure 5.93
Figure 5.94
CALCULATOR EXPLORATION AND DISCOVERY
0
024
3
Figure 5.95
0
024
3
Figure 5.96
cob19529_ch05_601-614.qxd 12/29/08 4:55 PM Page 611 epg HD 049:Desktop Folder:Satya 29/12/08:Coburn_do_t del-ch05:MHDQ092-SUMM:
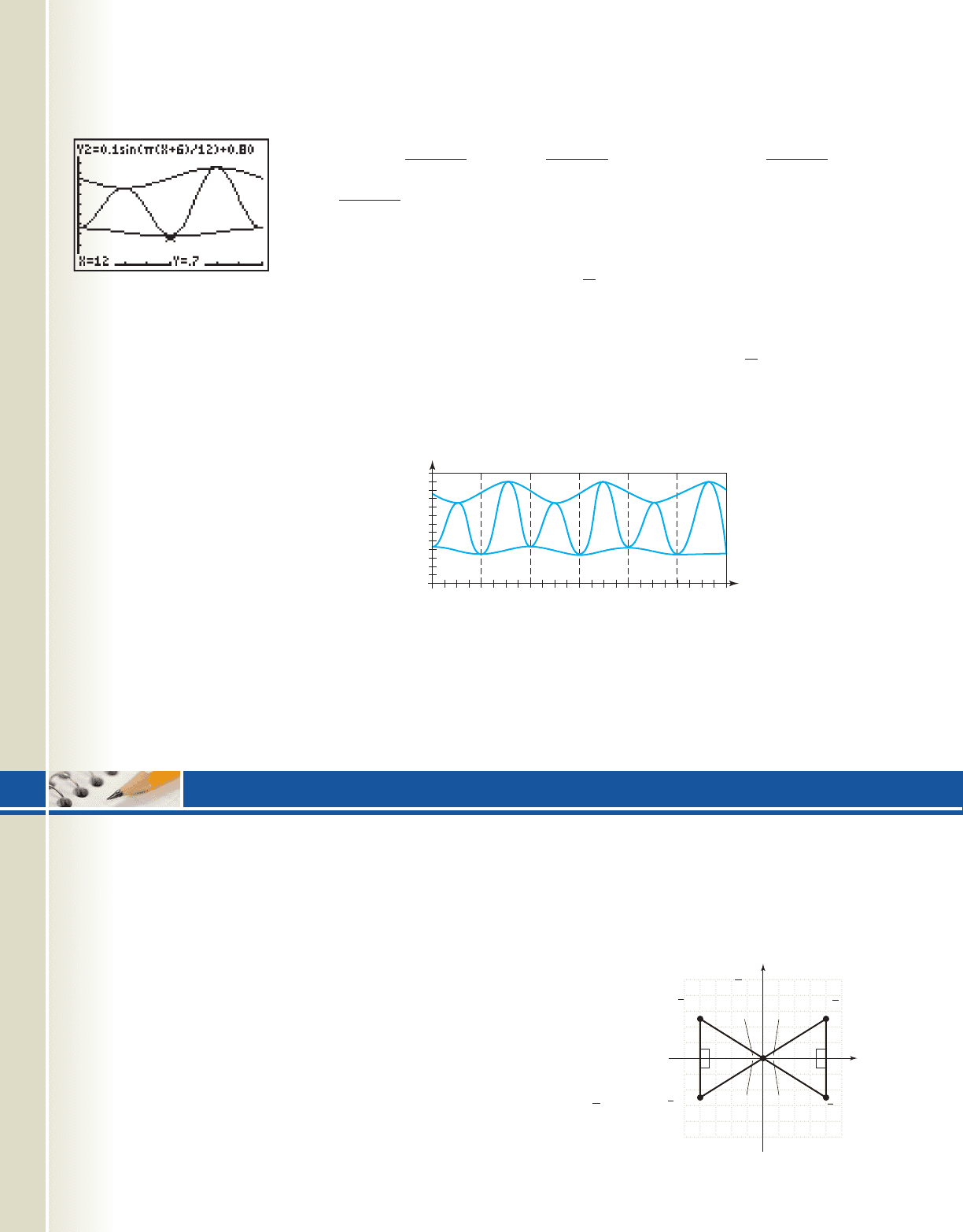
represents the low/high maximum values for high tide, and Y
2
represents the low/high
minimum values for low tide, the amplitude and average value for the tidal motion at Davis
Inlet are and By entering and
the equation for the tidal motion (with its variable amplitude) will have
the form where the value of B and C must be determined.
The key here is to note there is only a 12-hr difference between the changes in ampli-
tude, so (instead of 24) and for this function. Also, from the graph
(Figure 5.94) we note the tidal motion begins at a minimum and increases, indicating a
shift of 3 units to the right is required. Replacing x with gives the equation
modeling these tides, and the final equation is
Figure 5.97 gives a screen shot of Y
1
, Y
2
, and Y
5
in the interval [0, 24]. The tidal graph
from Figure 5.94 is shown in Figure 5.98 with Y
3
and Y
4
superimposed on it.
Exercise 1: The website www.tides.com/tcpred.htm offers both tide and current pre-
dictions for various locations around the world, in both numeric and graphical form.
In addition, data for the “two” high tides and “two” low tides are clearly highlighted.
Select a coastal area where tidal motion is similar to that of Davis Inlet, and repeat this
exercise. Compare your model to the actual data given on the website. How good was
the fit?
0.9
0.7
0.9
0.7
0.9
0.7
2.4
2.4
1.9
1.9 1.9
Y
2
Y
5
Y
1
2.4
t
Height (m)
0
1
2
Midni
g
ht Noon Midni
g
ht Noon Midni
g
ht Noon Midni
g
ht
Y
5
Y
3
sinc
6
1x 32d Y
4
.
x 3
B
6
P 12
Y
5
Y
3
sin1Bx C2 Y
4
,
Y
4
Y
1
Y
2
2
,
Y
3
Y
1
Y
2
2
D
Y
1
Y
2
2
!A
Y
1
Y
2
2
612 CHAPTER 5 An Introduction to Trigonometry 5-110
Figure 5.98
College Algebra & Trignometry—
Standard Angles, Reference Angles, and the Trig Functions
STRENGTHENING CORE SKILLS
out this study. Know the chart on page 550 and the ideas
that led to it.
The standard angles/values brought us to the
trigonometry of any angle, forming a strong bridge to
the second core skill:
(2) using reference
angles to determine
the value of the trig
functions in each
quadrant. For review,
a 30-60-90 triangle
will always have sides
that are in the propor-
tion
regardless of its size.
1x: 13
x:2x,
A review of the main ideas discussed in this chapter indi-
cates there are four of what might be called “core skills.”
These are skills that (a) play a fundamental part in the
acquisition of concepts, (b) hold the overall structure
together as we move from concept to concept, and (c) are
ones we return to again and again throughout our study.
The first of these is (1) knowing the standard angles and
standard values. These values are “standard” because no
estimation, interpolation, or special methods are required
to name their value, and each can be expressed as a single
factor. This gives them a great advantage in that further
conceptual development can take place without the main
points being obscured by large expressions or decimal
approximations. Knowing the value of the trig functions
for each standard angle will serve you very well through-
22
2
2
x
y
(√3, 1)
(√3, 1)
(√3, 1)
(√3, 1)
sin
r
2
1
2
2
2
2
r
30
r
30
r
30
r
30
Figure 5.99
0
3
024
Figure 5.97
cob19529_ch05_601-614.qxd 12/29/08 4:55 PM Page 612 epg HD 049:Desktop Folder:Satya 29/12/08:Coburn_do_t del-ch05:MHDQ092-SUMM:

5-111 Cumulative Review Chapters 1–5 613
College Algebra & Trignometry—
This means for any angle , where
or since the ratio is fixed but the sign
depends on the quadrant of :
[QI], [QII], [QIII],
[QIV], and so on (see Figure 5.99).
In turn, the reference
angles led us to a third core
skill, helping us realize that
if was not a quadrantal
angle, (3) equations like
must have
two solutions in
From the standard angles
and standard values we
learn to recognize that for
which will occur as a reference angle in the two quadrants
where cosine is negative, QII and QIII. The solutions in
are and (see Figure 5.100).
Of necessity, this brings us to the fourth core skill, (4)
effective use of a calculator. The standard angles are a
wonderful vehicle for introducing the basic ideas of
trigonometry, and actually occur quite frequently in real-
world applications. But by far, most of the values we
encounter will be nonstandard values where must be
found using a calculator. However, once is found,
the reason and reckoning inherent in these ideas can be
directly applied.
The Summary and Concept Review Exercises, as well
as the Practice Test offer ample opportunities to refine
these skills, so that they will serve you well in future chap-
ters as we continue our attempts to explain and understand
the world around us in mathematical terms.
r
r
210° 150°30, 360°2
r
30°,cos
13
2
,
30, 360°2.
cos12
13
2
sin 330°
1
2
sin 210°
1
2
sin 150°
1
2
sin 30°
1
2
sin
1
2
sin
1
2
r
30°,
Exercise 1: Fill in the table from memory.
t 0
Exercise 2: Solve each equation in without the use
of a calculator.
a.
b.
c.
d.
Exercise 3: Solve each equation in using a calcu-
lator and rounding answers to four decimal places.
a.
b.
c.
d. 2 sec t 5
3 tan t
1
2
1
4
312
cos t 12 0
16
sin t 2 1
30, 22
12
sec t 1 3
13
tan t 2 1
312
cos t 4 1
2 sin t 13
0
30, 22
5
4
7
6
5
6
3
4
2
3
tan t
y
x
cos t x
sin t y
2
3
4
6
CUMULATIVE REVIEW CHAPTERS 1–5
1. Solve the inequality given:
2. Find the domain of the function:
3. Given that draw a right triangle that
corresponds to this ratio, then use the Pythagorean
theorem to find the length of the missing side.
Finally, find the two acute angles.
4. Without a calculator, what values in make
the equation true: sin t
13
2
?
30, 22
tan
80
39
,
y 2x
2
2x 15
2
x 1
3 6 5
5. Given is a point on the unit circle
corresponding to t, find all six trig functions of t.
State the domain and range of each function shown:
6. 7. a.
b. g1x2
2x
x
2
49
x
y
55
5
5
f(x)
f1x2 12x 3y f1x2
a
3
4
,
17
4
b
22
2
2
x
y
(√3, 1)
(√3, 1)
cos
r
2
√3
2
2
150
210
r
30
r
30
Figure 5.100
cob19529_ch05_601-614.qxd 12/29/08 4:55 PM Page 613 epg HD 049:Desktop Folder:Satya 29/12/08:Coburn_do_t del-ch05:MHDQ092-SUMM:

614 CHAPTER 5 An Introduction to Trigonometry 5-112
8.
9. Analyze the graph of the function in Exercise 6,
including: (a) maximum and minimum values;
(b) intervals where and
(c) intervals where f is increasing or decreasing; and
(d) any symmetry noted. Assume the features you
are to describe have integer values.
10. The attractive force that exists between two magnets
varies inversely as the square of the distance between
them. If the attractive force is 1.5 newtons (N) at a
distance of 10 cm, how close are the magnets when
the attractive force reaches 5 N?
11. The world’s tallest indoor waterfall is in Detroit,
Michigan, in the lobby of the International Center
Building. Standing 66 ft from the base of the falls,
the angle of elevation is How tall is the
waterfall?
12. It’s a warm, lazy Saturday and Hank is watching a
county maintenance crew mow the park across the
street. He notices the mower takes 29 sec to pass
through of rotation from one end of the park to
the other. If the corner of the park is 60 ft directly
across the street from his house, (a) how wide is the
park? (b) How fast (in mph) does the mower travel
as it cuts the grass?
13. Graph using transformations of a parent function:
14. Graph using transformations of a parent function:
15. Find for all six trig functions, given the point
is a point on the terminal side of the
angle. Then find the angle in degrees, rounded to
tenths.
16. Given (a) in what quadrant does the arc
terminate? (b) What is the reference arc? (c) Find the
value of sin t rounded to four decimal places.
17. A jet-stream water sprinkler shoots water a distance
of 15 m and turns back-and-forth through an angle
of . (a) What is the length of the arc thatt 1.2 rad
t 5.37,
P19, 402
f12
g1x2 e
x1
2.
f1x2
1
x 1
2.
77°
60°.
f1x26 0;f1x2 0
y T1x2
the sprinkler reaches? (b) What is the area in m
2
of
the yard that is watered?
18. Determine the equation of graph shown given it is of
the form
19. Determine the equation of the graph shown given it
is of the form
20. In London, the average temperatures on a summer
day range from a high of to a low of
(Source: 2004 Statistical Abstract of the United
States, Table 1331). Use this information to write
a sinusoidal equation model, assuming the low
temperature occurs at 6:00
A.M. Clearly state the
amplitude, average value, period, and horizontal
shift.
21. The graph of a function f(x) is given. Sketch the
graph of
22. The volume of a spherical cap is given by
Solve for r in terms of V and h.
23. Find the slope and y-intercept:
24. Solve by factoring:
25. At what interest rate will $1000 grow to $2275 in
12 yr if compounded continuously?
4x
3
8x
2
9x 18 0.
3x 4y 8.
r
h
V
h
2
3
13r h2.
x
y
55
5
5
f
1
1x2.
56°F72°F
2
1
0
1
2
y
x
4
3
4
2
y A sin1Bt C2 D.
y
t
3
4
3
4
4
2
4
4
2
4
2
2
8
,
1
y A tan1Bt2.
xT(x)
0
1
2
3
41
53
65
1
3
5
7
cob19529_ch05_601-614.qxd 12/29/08 4:55 PM Page 614 epg HD 049:Desktop Folder:Satya 29/12/08:Coburn_do_t del-ch05:MHDQ092-SUMM:

Trigonometric
Identities, Inverses,
and Equations
CHAPTER OUTLINE
6.1 Fundamental Identities and
Families of Identities 616
6.2 Constructing and Verifying Identities 624
6.3 The Sum and Difference Identities 630
6.4 The Double-Angle, Half-Angle, and
Product-to-Sum Identities 640
6.5 The Inverse Trig Functions and
Their Applications 654
6.6 Solving Basic Trig Equations 671
6.7 General Trig Equations and Applications 682
6
6
CHAPTER CONNECTIONS
Have you ever noticed that people who arrive
early at a movie tend to choose seats about
halfway up the theater’s incline and in the
middle of a row? More than likely, this is due
to a phenomenon called the optimal viewing
angle, or the angle formed by the viewer’s
eyes and the top and bottom of the screen.
Seats located in this area maximize the
viewing angle, with the measure of the angle
depending on factors such as the distance
from the floor to the bottom of the screen, the
height of the screen, the location of a seat,
and the incline of the auditorium. Here,
trigonometric functions and identities play an
important role. This application appears as
Exercise 59 of Section 6.2.
Check out these other real-world connections:
Finding the Viewing Angle from a Seat
at the Theatre (Section 6.2, Exercise 64)
Modeling the Range of a Projectile
(Section 6.4, Exercise 109)
Maximizing the Shooting Angle during a
Break-away (Section 6.5, Exercise 95)
Modeling the Grade of a Treadmill during
a Workout Session (Section 6.7, Exercise 54)
615
College Algebra & Trignometry—
cob19529_ch06_615-623.qxd 12/29/2008 08:28 am Page 615

In this section we begin laying the foundation necessary to work with identities
successfully. The cornerstone of this effort is a healthy respect for the fundamental
identities and vital role they play. Students are strongly encouraged to do more than
memorize them—they should be internalized,meaning they must become a natural and
instinctive part of your core mathematical knowledge.
A. Fundamental Identities and Identity Families
An identity is an equation that is true for all elements in the domain. In trigonometry,
some identities result directly from the way the trig functions are defined. For instance,
since and , and the identity immediately
follows. We call identities of this type fundamental identities. Successfully working
with other identities will depend a great deal on your mastery of these fundamental
types. For convenience, the definition of the trig functions are reviewed here, followed
by the fundamental identities that result.
Given point P(x, y) on the unit circle, and the central angle associated with P,
we have and
Fundamental Trigonometric Identities
Reciprocal Ratio Pythagorean Identities due
identities identities identities to symmetry
These identities seem to naturally separate themselves into the four groups or fam-
ilies listed, with each group having additional relationships that can be inferred from
the definitions. For instance, since is the reciprocal of must be the
reciprocal of Similar statements can be made regarding and as well
as and . Recognizing these additional “family members” enlarges the
number of identities you can work with, and will help you use them more effectively.
In particular, since they are reciprocals:
See Exercises 7 and 8.
EXAMPLE 1
Identifying Families of Identities
Use algebra to write four additional identities that belong to the Pythagorean
family.
tan cot 1.
sin csc 1, cos sec 1,
cot tan
sec cos sin .
csc , csc sin
tan12tan 1 cot
2
csc
2
cot
cos
sin
tan
1
cot
cos12 cos tan
2
1 sec
2
tan
sec
csc
cos
1
sec
sin12sin sin
2
cos
2
1tan
sin
cos
sin
1
csc
cot
x
y
; y 0csc
1
y
; y 0sec
1
x
; x 0
tan
y
x
; x 0sin ycos x
2x
2
y
2
1
sin
1
csc
csc
r
y
,
1
csc
y
r
sin
y
r
616 6-2
Learning Objectives
In Section 6.1 you will learn how to:
A. Use fundamental identi-
ties to help understand
and recognize identity
“families”
B. Verify other identities
using the fundamental
identities and basic
algebra skills
C. Use fundamental identi-
ties to express a given
trig function in terms of
the other five
D. Use counterexamples
and contradictions to
show an equation is not
an identity
6.1 Fundamental Identities and Families of Identities
WORTHY OF NOTE
The word fundamental itself
means, “a basis or founda-
tion supporting an essential
structure or function”
(Merriam Webster).
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 8:18 PM Page 616 epg HD 049:Desktop Folder:11/11/08:z_PDF:

6-3 Section 6.1 Fundamental Identities and Families of Identities 617
Solution
Starting with
original identity
• subtract
• take square root
original identity
• subtract
• take square root
For the identities involving a radical, the choice of sign will depend on the
quadrant of the terminal side.
Now try Exercises 9 and 10
The four additional Pythagorean identities are marked with a “•” in Example 1.
The fact that each of them represents an equality gives us more options when attempt-
ing to verify or prove more complex identities. For instance, since
we can replace with or replace with any time they
occur in an expression. Note there are many other members of this family, since similar
steps can be performed on the other Pythagorean identities. In fact, each of the funda-
mental identities can be similarly rewritten and there are a variety of exercises at the
end of this section for practice.
B. Verifying an Identity Using Algebra
Note that we cannot prove an equation is an identity by repeatedly substituting input
values and obtaining a true equation. This would be an infinite exercise and we might
easily miss a value or even a range of values for which the equation is false. Instead
we attempt to rewrite one side of the equation until we obtain a match with the other
side, so there can be no doubt. As hinted at earlier, this is done using basic algebra skills
combined with the fundamental identities and the substitution principle. For now we’ll
focus on verifying identities by using algebra. In Section 6.2 we’ll introduce some
guidelines and ideas that will help you verify a wider range of identities.
EXAMPLE 2
Using Algebra to Help Verify an Identity
Use the distributive property to verify that is an
identity.
Solution
Use the distributive property to simplify the left-hand side.
distribute
substitute 1 for
Since we were able to transform the left-hand side into a duplicate of the right,
there can be no doubt the original equation is an identity.
Now try Exercises 11 through 20
Often we must factor an expression, rather than multiply, to begin the verification
process.
EXAMPLE 3
Using Algebra to Help Verify an Identity
Verify that is an identity.1 cot
2
x sec
2
x cot
2
x
1 sin
2
cos
2
cos
2
sin csc 1 sin
2
sin 1csc sin 2 sin csc sin
2
sin 1csc sin 2 cos
2
cos
2
,1 sin
2
1 sin
2
,cos
2
cos
2
1 sin
2
,
cos 21 sin
2
sin
2
cos
2
1 sin
2
sin
2
cos
2
1
sin 21 cos
2
cos
2
sin
2
1 cos
2
sin
2
cos
2
1
sin
2
cos
2
1,
A. You’ve just learned how
to use fundamental identities
to help understand and
recognize identity “families”
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 8:18 PM Page 617 epg HD 049:Desktop Folder:11/11/08:z_PDF:

618 CHAPTER 6 Trigonometric Identities, Inverses, and Equations 6-4
Solution
The left side is as simple as it gets. The terms on the right side have a common
factor and we begin there.
factor out
substitute for
power property of exponents
Now try Exercises 21 through 28
Examples 2 and 3 show you can begin the verification process on either the left or
right side of the equation, whichever seems more convenient. Example 4 shows how
the special products and/or
can be used in the verification process.
EXAMPLE 4
Using a Special Product to Help Verify an Identity
Use a special product and fundamental identities to verify that
is an identity.
Solution
Begin by squaring the left-hand side, in hopes of using a Pythagorean identity.
binomial square
rewrite terms
substitute 1 for
At this point we appear to be off by a sign, but quickly recall that sine is on odd
function and By writing as
we can complete the verification:
rewrite expression to obtain
✓
substitute for
Now try Exercises 29 through 34
Another common method used to verify identities is simplification by combining
terms, using the model For the right-
hand side immediately becomes , which gives See
Exercises 35 through 40.
C. Writing One Function in Terms of Another
Any one of the six trigonometric functions can be written in terms of any of the other
functions using fundamental identities. The process involved offers practice in working
with identities, highlights how each function is related to the other, and has practical
applications in verifying more complex identities.
EXAMPLE 5
Writing One Trig Function in Terms of Another
Write the function cos x in terms of the tangent function.
Solution
Begin by noting these functions share “common ground” via sec x, since
and Starting with sec
2
x,
Pythagorean identity
square roots
sec x 21 tan
2
x
sec
2
x 1 tan
2
x
cos x
1
sec x
.sec
2
x 1 tan
2
x
1
cos u
sec u.
sin
2
u cos
2
u
cos u
sec u
sin
2
u
cos u
cos u,
A
B
C
D
AD BC
BD
.
sin x
sin1x2 1 2 sin(x) cos x
sin x
1 21sin x21cos x2
1 21sin x21cos x2,1 2 sin x cos xsin x sin1x2.
sin
2
x cos
2
x
1 2 sin x cos x
sin
2
x cos
2
x 2 sin x cos x
1sin x cos x2
2
sin
2
x 2 sin x cos x cos
2
x
1sin x cos x2
2
1 2 sin(x) cos x
1A B2
2
A
2
2AB B
2
1A B21A B2 A
2
B
2
cot x tan x 1
1
2
1
1cot x tan x2
2
sec
2
x 1tan
2
x
cot
2
x tan
2
x
cot
2
x
cot
2
x sec
2
x cot
2
x cot
2
x 1sec
2
x 12
B. You’ve just learned how
to verify other identities using
the fundamental identities and
basic algebra skills
College Algebra & Trignometry—
cob19529_ch06_615-700.qxd 11/11/08 8:18 PM Page 618 epg HD 049:Desktop Folder:11/11/08:z_PDF:

6-5 Section 6.1 Fundamental Identities and Families of Identities 619
We can now substitute for sec x in
substitute for sec x
Now try Exercises 41 through 46
Example 5 also reminds us of a very important point — the sign we choose for the
final answer is dependent on the terminal side of the angle. If the terminal side is in QI
or QIV we chose the positive sign since in those quadrants. If the angle ter-
minates in QII or QIII, the final answer is negative since in those quadrants.
Similar to our work in Chapter 5, given the value of cot t and the quadrant of t, the
fundamental identities enable us to find the value of the other five functions at t. In fact,
this is generally true for any given trig function and real number or angle t.
EXAMPLE 6
Using a Known Value and Quadrant Analysis to Find Other Function Values
Given with t in QIV, find the value of the other five functions at t.
Solution
The function value follows immediately, since cotangent and tangent
are reciprocals. The value of sec t can be found using
Pythagorean identity
substitute for tan t
square , substitute for 1
combine terms
take square roots
Since sec t is positive in QIV, we have This automatically gives
(reciprocal identities), and we find using
or the ratio identity (verify).
Now try Exercises 47 through 55
D. Showing an Equation Is Not an Identity
To show an equation is not an identity, we need only find a single value for which the
functions involved are defined but the equation is false. This can often be done by trial
and error, or even by inspection. To illustrate the process, we’ll use two common mis-
conceptions that arise in working with identities.
EXAMPLE 7
Showing an Equation is Not an Identity
Show the equations given are not identities.
a. b. cos1 2 cos cos sin12x2 2 sin x
tan t
sin t
cos t
sin
2
t 1 cos
2
tsin t
40
41
cos t
9
41
sec t
41
9
.
sec t
41
9
1681
81
81
81
40
9
81
81
1600
81
40
9
1 a
40
9
b
2
sec
2
t 1 tan
2
t
sec
2
t 1 tan
2
t.
tan t
40
9
cot t
9
40
cos x 6 0
cos x 7 0
21 tan
2
xcos x
1
21 tan
2
x
cos x
1
sec x
.21 tan
2
x
WORTHY OF NOTE
It is important to note the
stipulation “valid where both
are defined” does not
preclude a difference in the
domains of each function.
The result of Example 5 is
indeed an identity, even
though the expressions have
unequal domains.
College Algebra & Trignometry—
C. You’ve just learned
how to use fundamental
identities to express a given
trig function in terms of the
other five
cob19529_ch06_615-700.qxd 11/11/08 8:18 PM Page 619 epg HD 049:Desktop Folder:11/11/08:z_PDF:
