Цитович Б.В. Лекции по теоретической метрологии
Подождите немного. Документ загружается.

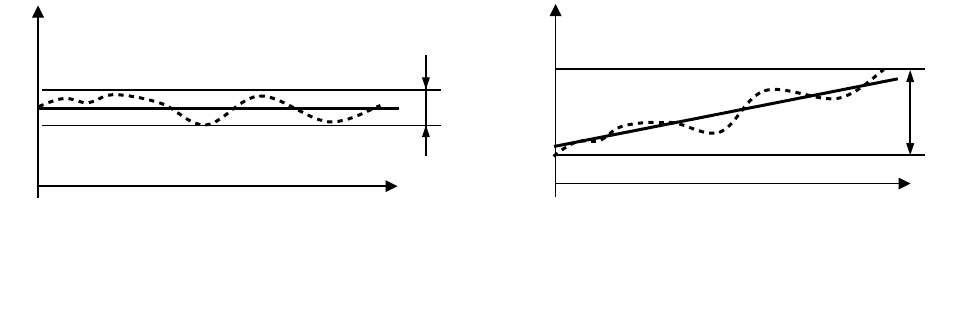
Размах R' включает в себя как рассеяние результатов из-за случайной составляющей
погрешности измерений, так и переменную систематическую составляющую погрешности (при ее
наличии), вызывающую закономерное изменение результатов во времени. Для того чтобы можно
было отдельно рассматривать влияние на измерения детерминированных и стохастических
воздействий, из результатов измерений исключают систематические составляющие погрешностей.
Такую операцию называют «исправлением результатов измерений», а результаты измерений
после исключения из них систематических погрешностей считают «исправленными». В
соответствии со сказанным, следует различать размахи «неисправленных» R' и «исправленных» R
результатов измерений.
Полное исправление результатов требует абсолютной строгости в определении
систематических составляющих погрешностей каждого из результатов измерений, что
невозможно осуществить с помощью точечной диаграммы. Даже если принятые при ее
построении допущения соответствуют реальной ситуации, постоянная составляющая
систематических погрешностей всегда остается невыявленной. Однако с использованием
точечной диаграммы можно осуществить «частичное исправление» результатов измерений. Для
этого на экспериментальные точки накладывают аппроксимирующую линию, которая отражает
изменения результатов из-за систематических погрешностей. Если считать, что отклонения
результатов от построенной тенденции их изменения вызваны собственно случайными
составляющими погрешности, можно перейти к их количественной оценке.
В этом случае делается допущение, что аппроксимирующая линия полностью отражает
систематические изменения результатов (линия «текущего среднего значения»), а отклонения от
этой линии рассматривают как случайные составляющие погрешности каждого из наблюдений.
Числовые оценки отклонений определяют по точечной диаграмме с учетом ее масштаба.
Предложенный прием позволяет разделить и наглядно представить на диаграмме систематические
и случайные составляющие погрешности измерений.
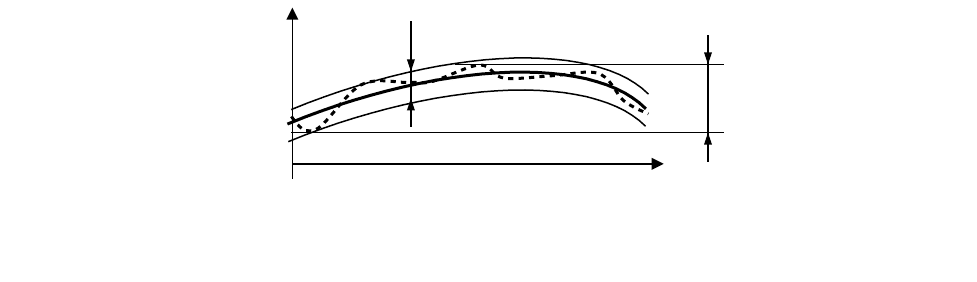
Для оценки размаха R «исправленных» результатов измерений, который отражает
рассеяние результатов из-за наличия только случайной составляющей погрешности, с помощью
диаграммы исключают влияние переменной систематической составляющей погрешности. Размах
R (рисунок 7.4) определяют как расстояние между двумя линиями, проведенными эквидистантно
аппроксимирующей линии через две наиболее удаленные от нее точки, а его значение
рассчитывают с учетом масштаба точечной диаграммы.
Описанное «исправление» результатов измерений названо частичным, поскольку
неизвестное (и потому отсутствующее на диаграмме) истинное значение измеряемой величины
искусственно заменяется некоторым «текущим средним значением». «Текущее среднее значение»
Х Х
R' R'
N N
а б
Рисунок 7.3 – Размахи R' результатов на точечных диаграммах без тенденции изменения
результатов а и с прогрессирующей тенденцией б
воспроизводится на диаграмме аппроксимирующей линией, учитывающей влияние переменной
части систематической погрешности.
Точечная диаграмма результатов многократных измерений физической величины,
полученных с помощью одной методики выполнения измерений, не дает представления о
значении постоянной систематической погрешности. Диаграмма одной серии не содержит
достаточной информации для такого анализа из-за отсутствия «опорного значения», которым
можно было бы заменить истинное.
Анализ результатов измерений каждой отдельной серии обычно начинают с выявления
тенденции изменения результатов измерений и ее качественной оценки. Затем на диаграмму
наносят аппроксимирующую линию, соответствующую характеру изменения результатов серии.
При анализе диаграмм могут встретиться три варианта:
серия без тенденции изменения результатов;
серия без явно выраженной тенденции изменения результатов;
серия c явной тенденцией изменения результатов.
Первый вариант свидетельствует об отсутствии в серии переменной систематической
погрешности, диаграмму аппроксимируют прямой линией, параллельной оси абсцисс. Такая
аппроксимация свидетельствует о наличии в серии постоянной систематической составляющей
погрешности, значение которой оценить невозможно (это может быть значимая либо
пренебрежимо малая погрешность).
При отсутствии в серии явно выраженной тенденции изменения результатов ее также как и
в первом варианте аппроксимируют прямой линией, параллельной оси абсцисс.
Для аппроксимации диаграмм третьего варианта по возможности выбирают наклонные
прямые линии (линейно прогрессирующее в сторону увеличения или уменьшения изменение
результатов) или простейшие кривые линии в виде параболы, дуги окружности, синусоиды
(прогрессирующее изменение с затуханием, модальное или периодическое изменение
результатов). При любой аппроксимации обязательно будут наблюдаться несовпадение
результатов и аппроксимирующей линии. Отклонения могут быть вызваны объективными
причинами (наличие случайных погрешностей в результатах измерений), или несоответствующей
аппроксимацией результатов (неправильный характер и расположение аппроксимирующей
линии). Успешность выбора аппроксимирующей зависимости и ее наложения на
экспериментальные точки зависит от числа наблюдений и опыта исследователя. Можно проводить
аппроксимирующие линии выбранного вида с использованием математических методов
(например, метода наименьших квадратов), но точность и достоверность результатов при этом
практически не повышается. Поскольку сами погрешности имеют малые значения, а анализ
точечных диаграмм основан на допущениях, не обеспечивающих высокий уровень строгости,
незначительные погрешности аппроксимации, как правило, имеют второй порядок малости и
X R
R'
N
Рисунок 7.4 – Размах R' неисправленных результатов и размах R, характеризующий
рассеяние результатов относительно тенденции их изменения («текущего среднего значения»)
«погрешности оценки погрешностей» не приводят к существенному искажению результатов
исследования.
Чаще всего аппроксимация простейшими линиями оказывается достаточно эффективной,
но не исключаются и возможные уточнения, например использование параболы или экспоненты
для описания участка прогрессирующих данных или наложение синусоиды на наклонную прямую
линию. Однако при этом следует иметь в виду, что стремление к высокой точности в подборе
аппроксимирующей линии не имеет смысла, поскольку не гарантирована строгость соответствия
точечной диаграммы допущениям, положенным в основу ее построения. Как показывает опыт
анализа точечных диаграмм, незначительные различия при моделировании систематических
тенденций разными исследователями при оценивании погрешностей приводят к расхождениям
второго порядка малости и не оказывают значимого влияния на результаты таких числовых
оценок как среднее квадратическое отклонение.
Примерами серий с очевидными тенденциями можно считать точечные диаграммы на
рисунке 7.2. На рисунке 7.2а просматривается тенденция увеличения результатов, которую проще
всего аппроксимировать прямой линией. Такая тенденция свидетельствует о наличии в
результатах прогрессирующей систематической погрешности линейного характера. Тенденция на
рисунке 7.2б – немонотонная, результаты сначала увеличиваются, затем после достижения
максимума уменьшаются, что позволяет предложить аппроксимацию дугой окружности или
участком синусоиды. Немонотонное изменение результатов может свидетельствовать о наличии
периодической систематической составляющей, однако для уверенного заключения об этом
экспериментальных данных явно недостаточно. Зато на рисунке 7.2в очевидно просматривается
периодическая тенденция, которую можно аппроксимировать косинусоидой в 3/4 периода.
После проведения аппроксимирующей линии визуально оценивают экстремальные
отклонения от этой линии. При наличии одной или нескольких точек, явно выпадающих из общей
тенденции, делается отрицательное заключение об их принадлежности исследуемому массиву
результатов измерений. Результаты, соответствующие этим точкам, оценивают как содержащие
грубые погрешности и цензурируют, полагая, что они получены ошибочно. Результаты,
подозрительные на наличие промахов, но вызывающие сомнения, оставляют для последующего
статистического отбраковывания, которое выходит за пределы анализа точечных диаграмм.
Если не наблюдается резко выпадающих из общей тенденции отклонений (результатов с
грубыми погрешностями), то через самые удаленные от аппроксимирующей линии точки
(максимальные отклонения «в плюс» и «в минус») проводят эквидистанты аппроксимирующей
линии. Расстояние между ними вдоль оси ординат в масштабе точечной диаграммы равно размаху
отклонений R, и рассматривается как одна из характеристик случайной составляющей
погрешности анализируемой серии.
Проведенные на точечной диаграмме аппроксимирующая линия и эквидистанты позволяют
количественно оценить не только размахи отклонений R' (общий размах результатов измерений) и
R (размах частично исправленных результатов измерений), но и другие параметры и
характеристики точечной диаграммы, включая изменение прогрессирующей составляющей в
серии результатов (приращение а в пределах серии), амплитуду А или удвоенную амплитуду 2А
периодической составляющей, а также ее ориентировочный период Т в числах (номерах)
наблюдений.
Точечная диаграмма в определенных случаях позволяет высказать некоторые суждения не
только о сходимости результатов в серии, но и о правильности измерений, поскольку устойчивая
тенденция изменения результатов измерений свидетельствует о наличии в них переменной
систематической погрешности. Анализ точечных диаграмм позволяет делать логически
обоснованные предположения об изменении условий измерений в самом широком понимании
этого термина. Например, наличие прогрессирующей тенденции в серии измерений может быть
связано с закономерным изменением одной или нескольких влияющих величин, накапливающейся
усталостью оператора, накапливающимся воздействием чувствительного элемента на объект
измерений. Предположения об износе элементов измерительной цепи средства измерений, как
правило, неправомочны, поскольку существенный износ деталей прибора при проведении
нескольких десятков или даже сотен измерений может наблюдаться только у особо неудачных
конструкций или отдельных экземпляров средств измерений.
Ниже приведены точечные диаграммы (рисунок 7.5), на основании которых проведен
анализ результатов измерений каждой из проведенных серий и примеры гипотетических
высказываний о возможных причинах характерных особенностей результатов в сериях.
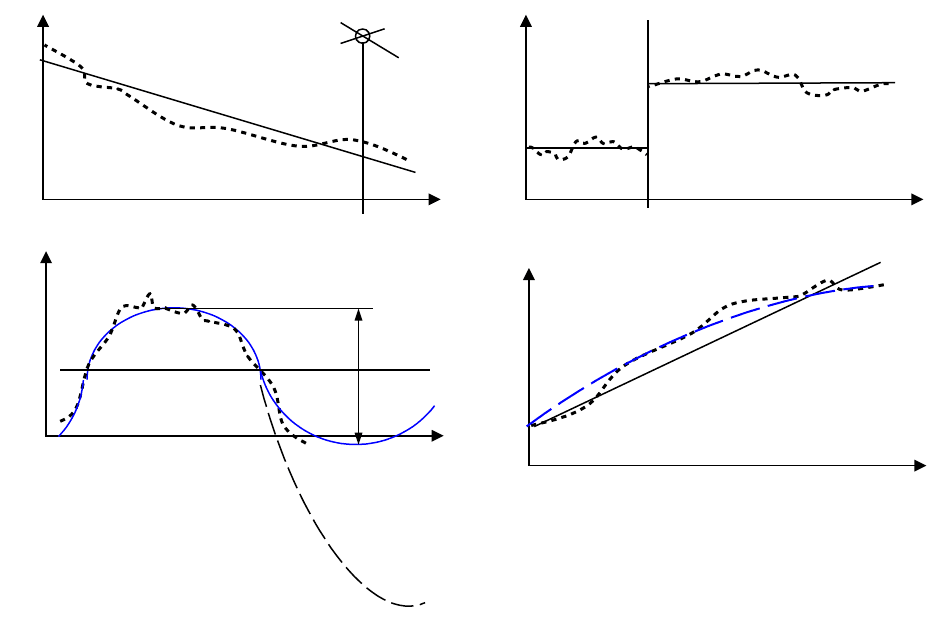
Точечная диаграмма на рисунке 7.5а имеет явно выраженную тенденцию монотонного
убывания значений, что свидетельствует о наличии в серии прогрессирующей погрешности
(тенденция изменения отражена аппроксимирующей прямой). Результат n
j
цензурируется как
результат с грубой погрешностью – он явно выпадает из общей тенденции, несмотря на то, что его
значение близко к значениям в начале серии. Возможные причины появления этого результата –
ошибка оператора (промах при манипулировании или при отсчитывании) либо сбой в работе
прибора.
Особенностью точечной диаграммы на рисунке 7.5б является очевидное наличие двух
участков 1 и 2, каждый из которых не имеет явно выраженной тенденции изменения результатов.
Резкое (скачкообразное) изменение результатов между участками 1 и 2 свидетельствуют о
фактическом изменении условий измерений в серии в широком смысле этого термина (возможно,
произошло незамеченное изменение влияющей величины, изменилась измеряемая величина, был
заменен оператор или случилось некое иное событие), результатом чего стало получение двух
серий вместо одной.
Скачкообразное изменение результатов позволяет высказать несколько предположений:
возможно, был перерыв в работе, за время которого изменились условия измерений (одна или
несколько влияющих величин), могло произойти мгновенное изменение настройки (сбой
настройки) прибора. В качестве гипотезы можно также рассмотреть возможную «подмену»
измеряемой физической величины, то есть фактический переход от одной из номинально
одинаковых физических величин к другой, например, из-за незамеченного изменения
контрольного сечения (контрольной точки).
Точечная диаграмма на рисунке 7.5в имеет явно выраженную тенденцию немонотонного
изменения значений, что может свидетельствовать о наличии в серии периодической
(циклической) погрешности. Возможные тенденции изменения результатов отражены двумя
аппроксимирующими линиями – сплошной и штриховой, из которых видно, что предполагаемые
тенденции примерно вдвое различаются по периоду и амплитудам. Поскольку для достоверных
заключений о наличии периодической погрешности, ее амплитуде и предполагаемом периоде
наличной информации недостаточно, по возможности следует продолжить серию измерений, при
невозможности – высказать предположения, четко оговаривая принятые допущения.
При выполнении нескольких серий многократных измерений одной и той же физической
величины с использованием разных методик выполнения измерений весьма эффективно их
сопоставление с помощью точечных диаграмм, построенных в одном масштабе. Анализ каждой из
серий измерений включает оценку отдельно по каждой серии тенденций изменения результатов
измерений и оценки размахов Ri.
Сравнительный анализ результатов нескольких серий измерений одной и той же
физической величины позволяет оценить воспроизводимость измерений. Характеристиками
воспроизводимости измерений в двух сериях могут быть значения размахов и расхождение
средних значений при практическом отсутствии тенденции изменения результатов, поскольку
переменные систематические погрешности обязательно приведут к низкой сходимости
результатов в серии и воспроизводимости серий. В случае неравноточных МВИ можно получить
также предварительную оценку систематических постоянных погрешностей для заведомо менее
точной серии. Для оценки систематических постоянных погрешностей серию сравнивают с более
точной «опорной» серией, если в ней не наблюдаются явные тенденции изменения результатов.
Сходимость измерений в каждой из серий и между двумя сериями можно оценить по
систематическим расхождениям и отклонениям от аппроксимирующих линий (расхождениями
текущих средних и размахами), причем возможную сходимость оценивают по размахам после
«исправления результатов» (исключения влияния тенденции изменения результатов, если она
обнаружена). О правильности измерений можно судить по значениям размахов Ri и по числовым
характеристикам тенденций изменения результатов. Можно ожидать высокой правильности
только в той серии, в которой размахи минимальны и тенденции изменения результатов
практически отсутствуют.
X X
1 2
n
j
N N
а б
X
X
2A a1
a2
N
N
в г
Рисунок 12 – Примеры точечных диаграмм с элементами графического анализа
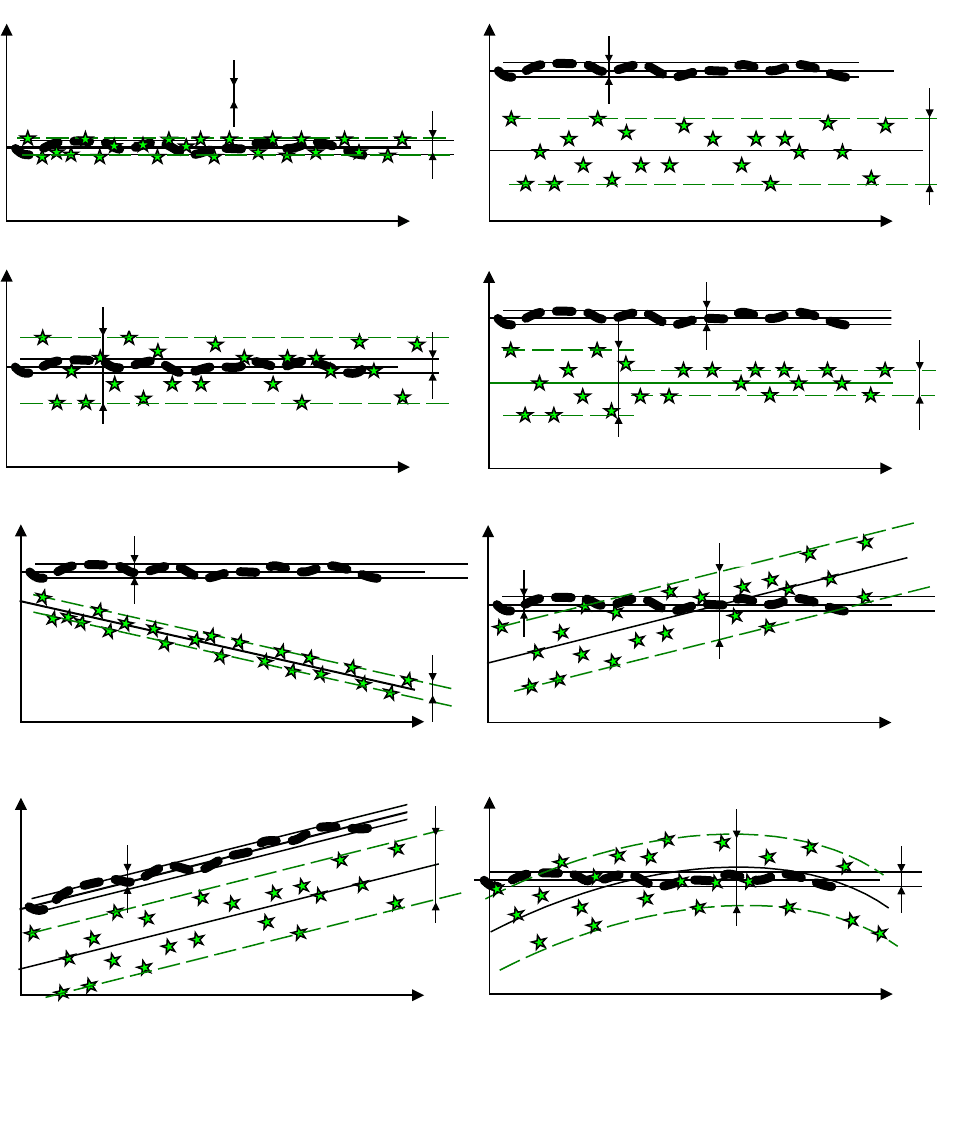
Все характеристики особенно хорошо видны на точечной диаграмме с двумя сериями
измерений, оформленными в одном масштабе. Примеры таких точечных диаграмм с элементами
анализа приведены на рисунках 7.6 а – 7.6 з.
а б
в г
д е
ж з
Приведем примеры краткого сравнительного анализа двойных диаграмм, представленных
на рисунке 7.6.
В тексте использованы уже встречавшиеся обозначения размахов «исправленных
результатов» (R), средних значений серии наблюдений (X) и истинного значения измеряемой
физической величины (Q).
R
1
R
2
R
1
R
2
R'
2
R
2
R
1
R
1
R"
2
R
1
R
2
R
1
R
2
R
2
R
1
R
2
R
1
Рисунок 7.6 – Примеры «парных» точечных диаграмм. Точками представлена
«опорная» диаграмма, полученная при использовании более точной МВИ 1,
звездочками – диаграмма, полученная при использовании менее точной МВИ 2.
Значения размахов «неисправленных результатов», средние значения каждой из серий и
истинные значения измеряемой физической величины на точечных диаграммах не показаны,
чтобы не загромождать рисунок. Подробный анализ каждой из диаграмм не проводится,
поскольку примеры такого анализа были представлены ранее.
На диаграмме 7.6а представлены две серии без переменных систематических погрешностей
(в обеих сериях отсутствуют тенденции изменения результатов), которые можно считать
практически равнорассеянными, (поскольку R
1
≈ R
2
), но неравноточными (поскольку Х
1
≠ Х
2
).
Неравенство средних значений свидетельствует о том, что либо одна, либо обе имеют постоянные
систематические составляющие, значимые по сравнению со случайными составляющими (Х
1
– Х
2
> R
1
≈ R
2
).
Серии на диаграмме 7.6б без переменных систематических погрешностей,
неравнорассеянные (поскольку R
1
≠ R
2
) и неравноточные (в них кроме того, что R
1
≠ R
2
, еще и Х
1
≠
Х
2
), причем либо в одной, либо в обеих сериях присутствуют постоянные систематические
погрешности (если, например, считать Х
1
≈ Q, то Х
2
≠ Q, поскольку Х
1
≠ Х
2
).
На диаграмме 7.6в показаны серии без переменных систематических погрешностей
неравноточные и неравнорассеянные (R
1
≠ R
2
), причем обе имеют практически одинаковые
постоянные систематические составляющие (поскольку Х
1
≈ Х
2
).
На диаграмме 7.6г представлены две серии без переменных систематических
погрешностей, неравнорассеянные (поскольку R
1
≠ R
2
), причем более грубая серия имеет два
характерных участка с различающимися размахами (видно, что R'
2
≠ R"
2
). Серии неравноточные,
поскольку кроме неравенства случайных погрешностей еще и Х
1
≠ Х
2
, следовательно различны и
постоянные систематические погрешности). Одна из серий, либо обе имеют значимые постоянные
систематические составляющие (поскольку Х
1
≠ Х
2
) .
Первая серия на диаграмме 7.6д не имеет переменных систематических погрешностей, у
второй – явно выраженная тенденция изменения результатов (значения монотонно убывают, что
свидетельствует о наличии прогрессирующей систематической составляющей). Серии
неравноточные (R'
1
≠ R'
2
), но можно графически или аналитически привести их к практически
равнорассеянным (поскольку R
1
≈ R
2
), для чего необходимо исключить из рассмотрения
переменную систематическую составляющую второй серии.
На диаграмме 7.6е представлены две серии очевидно неравноточные и неравнорассеянные.
Первая серия не имеет переменных систематических погрешностей, у второй явно выраженная
прогрессирующая тенденция изменения результатов (значения монотонно возрастают, что
свидетельствует о наличии прогрессирующей систематической составляющей).
Две явно неравноточные и неравнорассеянные серии на диаграмме 7.6ж имеют примерно
одинаковые прогрессирующие тенденции изменения результатов (однотипные возрастающие
значения свидетельствуют о наличии практически одинаковых прогрессирующих
систематических составляющих).
На последней диаграмме 7.6з представлены две явно неравноточные и неравнорассеянные
серии, одна из которых имеет немонотонную тенденцию изменения результатов (вначале
возрастающие, а затем убывающие значения свидетельствуют о наличии систематической
составляющей, предположительно циклического характера). Для достоверных заключений о
наличии во второй серии периодической погрешности, ее амплитуде и предполагаемом периоде
наличной информации недостаточно.
МОДУЛЬ 8. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА И ФОРМЫ ПРЕДСТАВЛЕНИЯ
РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
В ходе решения различных измерительных задач часто встречается необходимость
математической обработки результатов измерений. В литературных источниках описание
математической обработки результатов измерений часто сведено к статистической обработке
некоторых абстрактных данных, свободных от систематической составляющей, что фактически
отражает только одну сторону проблемы.
Анализ математической обработки результатов измерений позволяет выделить следующие
типовые задачи:
- обработка результатов прямых многократных измерений одной и той же физической
величины (серии измерений);
- расчет результатов косвенных измерений физической величины, в том числе при
многократных прямых измерениях каждой из величин, входящих в формулу для расчета
результатов косвенных измерений;
- обработка результатов измерений массива номинально одинаковых величин;
- обработка результатов измерений разных величин или изменяющейся физической
величины.
Третий и четвертый случаи выходят за рамки чистой метрологии, поскольку относятся к
более широкому классу задач, решаемых в ходе проведения экспериментальных исследований.
В метрологии для повышения достоверности и представительности результатов достаточно
часто прибегают к многократным повторениям операции измерений одной и той же физической
величины. При этом каждый единичный результат называют наблюдением при измерении, а
результат измерений получают как интегральную оценку всего массива наблюдений. Поэтому в
метрологии под математической обработкой результатов измерений традиционно понимают
обработку результатов многократных прямых или косвенных измерений одной и той же
физической величины.
Математическая обработка включает два принципиально разных направления:
детерминированную обработку результатов измерений и статистическую обработку.
Детерминированная математическая обработка результатов измерений в обязательном порядке
применяется при получении результатов косвенных измерений. Например, для определения
плотности некоторого вещества измеряют массу и объем одного и того же образца, после чего
рассчитывают его плотность. В линейно-угловых измерениях часто рассчитывают угол по
результатам измерений длин, межосевые расстояния отверстий по координатам осей и т.д.
При наличии систематических тенденций изменения результатов многократных измерений
одной и той же величины также можно применить детерминированную математическую
обработку результатов. В ходе этой обработки стремятся получить аналитическое описание
систематической составляющей погрешности измерений. Такое описание позволяет исключить
из дальнейшего рассмотрения переменные систематические погрешности. Результаты
измерений, из которых исключены систематические погрешности, в метрологии называют
«исправленными». Данные после полного или частичного «исправления» можно подвергать
статистической обработке. Под «частичным исправлением» мы понимаем исключение переменной
систематической составляющей погрешности. В таком случае математическая обработка
позволяет получить неискаженные оценки вида распределения и его моментов, кроме оценки
математического ожидания (она может оказаться смещенной из-за неисключенной постоянной
составляющей систематической погрешности).
Задача обработки массива результатов измерений номинально одинаковых величин может
появиться в ходе измерительного контроля неидеального объекта с множеством однородных
физических величин, заданных одним параметром. Если расхождения результатов в предыдущих
группах задач были обусловлены только погрешностями измерений, то в рассматриваемой задаче
сами измеряемые величины могут существенно различаться. Например, шарик для подшипника
качения не является идеальной сферой и имеет бесконечное число толщин, которые нормированы
как один диаметральный размер. Еще более сложные задачи возникают при контроле партии
однородной продукции по одному из параметров, при измерениях номинально одинаковых
физических величин, многократно воспроизводимых в ходе экспериментальных исследований
технологических процессов и т.д.
Последняя задача – обработка результатов измерений разных величин или изменяющейся
физической величины – характерна для экспериментальных исследований, связанных с
выявлением характера изменения исследуемой величины (параметра) при контролируемом
изменении одного или нескольких аргументов. В метрологии такие задачи характерны для
поверки и калибровки средств измерений, а также для метрологической аттестации средств
измерений и методик выполнения измерений.
Отсутствие четкой постановки задачи обработки результатов измерений часто приводит к
недоразумениям, в том числе к искажению получаемых результатов за счет перемешивания
случайных (стохастических) результатов воспроизведения измеряемых величин и случайных
погрешностей измерений этих величин. Дополнительные искажения могут внести неисключенные
систематические составляющие, вне зависимости от источников их появления (возможны
систематические изменения при многократном воспроизведении номинально одинаковых
измеряемых величин и/или систематические погрешности измерений одной физической
величины).
Статистическая обработка некоторых произвольных «исправленных» результатов (любых
стохастически изменяющихся значений, будь то результаты измерений или результаты
многократного воспроизведения номинально одинаковых величин) рассмотрена во многих
литературных источниках. Корректно выполненная статистическая обработка «исправленных»
результатов измерений отличается строгой постановкой задачи и соблюдением требований
метрологической нормативной документации (ГОСТ 8.207-76, МИ 1317-86 и др.).
Статистическая обработка исправленных результатов прямых измерений
Подготовка массива результатов измерений к статистической обработке заключается в
«исправлении результатов измерений». Задача-максимум состоит в исключении из результатов
измерений всех систематических составляющих, задача минимум – в исключении переменных
систематических составляющих. Следует признать, что любое исключение погрешностей не
бывает абсолютным; в результатах могут содержаться невыявленные систематические
составляющие, а также всегда остаются неисключенные остатки систематических
погрешностей. Методы выявления, оценки и исключения систематических погрешностей и
методы оценки неисключенных остатков систематических погрешностей рассмотрены в
соответствующем модуле.
Рассмотрим порядок статистической обработки исправленных результатов прямых
равнорассеянных измерений одной и той же физической величины.
1. Расчет среднего арифметического значения X
ср
(получение точечной оценки результата
измерения)
n
X
ср
= Σ X
i
.
i =1
2. Расчет отклонений V
i
результатов наблюдений от среднего арифметического
V
i
= X
ср
– X
i
.
2a. Проверка правильности расчетов значений отклонений и среднего арифметического
n
Σ V
i
≈ 0.
i =1
Если сумма значимо отличается от нуля, то либо неправильно рассчитаны отклонения, либо
среднее арифметическое значение и отклонения. Несущественные отклонения от нуля возможны
из-за округления среднего арифметического.
3. Расчет оценки с к о результатов наблюдений
_________________________
˜ /
n
σ
X
= √ [1/(n-1)] ∙ Σ (Xср – Xi)
2
i =1
4. Проверка гипотезы о сходимости эмпирического и теоретического распределений по
критериям согласия.
При n > 50 для проверки принадлежности распределения к нормальному предпочтительно
использование критериев Пирсона
2
(рекомендуется использовать при n > 100) или Мизеса-
Смирнова
2
. При 15 < n < 50 для проверки принадлежности распределения к нормальному
предпочтительным является составной критерий (W).
Проверки по критериям согласия проводят при уровне значимости q от 10 % до 2 %.
Принятые значения уровней значимости приводят в описании методики выполнения измерений
или обработки результатов измерений.
При n ≤ 15 проверку принадлежности распределения к нормальному не проводят, а
качественную оценку формируют на основе априорной информации о виде (законе)
распределения случайной величины, что позволяет затем перейти к соответствующей
количественной оценке.
5. Статистическая проверка наличия результатов с грубыми погрешностями.
При наличии результатов, подозрительных на наличие грубой погрешности, определяют
критерий ν для статистического отбраковывания экстремальных результатов X
extr
и сравнивают его
с критическим значением ν'
ν = ( |X
extr
– X
ср
| / σ) > ν'.
При нормальном распределении погрешностей можно применять упрощенную процедуру
отбраковывания экстремальных отклонений, например, по критерию 3σ
|V
extr
| > 3σ.
Соблюдение неравенства позволяет утверждать, что проверяемый результат содержит
грубую погрешность и должен исключаться из рассмотрения. Если отбракован хотя бы один
результат с грубой погрешностью обработка повторяется с п.1.
6. Расчет оценки среднего квадратического отклонения результата измерения (оценки с к о
среднего арифметического значения)
˜
˜
__
σ
Xср
= σ
X
/√ n
7. Расчет значения границы погрешности результата измерения Δ (по модулю)
Δ = t σ
Xср
;
где t – коэффициент Стьюдента, зависящий от числа результатов наблюдений n и принятой
доверительной вероятности Р;
