CIMA - C3 Fundamentals Of Business Mathematics

Подождите немного. Документ загружается.

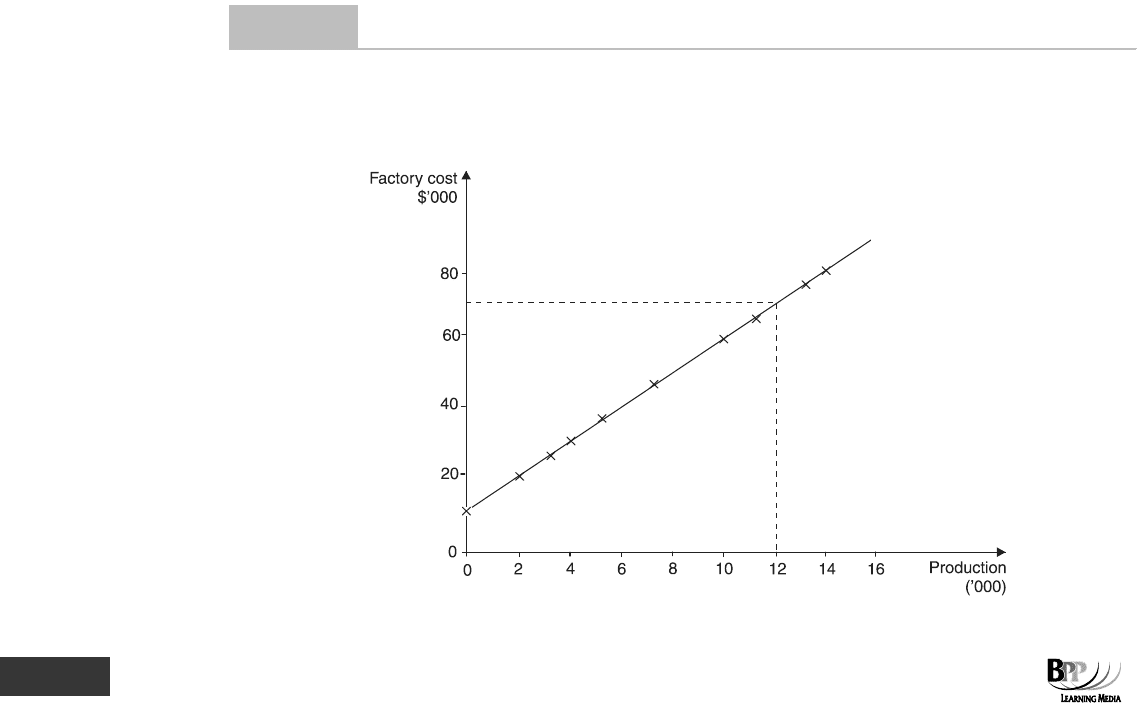
110 3: Data presentation ⏐ Part B Summarising and analysing data

Month Production Factory cost

Thousands $'000

20X8

November 7 45

December 10 59

20X9

January 13 75

February 14 80

March 11 65

April 7 46

May 5 35

June 4 30

July 3 25

August 2 20

September 1 15

October 5 35

You may assume that the value of money remained stable throughout the year.

Required

(a) Draw a scatter diagram related to the data provided above, and plot on it the line of best fit.

(b) Now answer the following questions.

(i) What would you expect the factory cost to have been if 12,000 widgets had been produced in a

particular month?

(ii) What is your estimate of WDG

's monthly fixed cost?

Answe

Your answers to parts (b)(i) and (ii) may have been slightly different from those given here, but they should not

have been very different, because the data points lay very nearly along a straight line.

(a) WDG Co – Scatter diagram of production and factory costs, November 20X8-October 20X9

Part B Summarising and analysing data ⏐ 3: Data presentation 111

(b) (i) The estimated factory cost for a production of 12,000 widgets is $70,000.

(ii) The monthly fixed costs are indicated by the point where the line of best fit meets the vertical axis

(costs at zero production). The fixed costs are estimated as $10,000 a month.

7 Using spreadsheets

Excel includes the facility to produce a range of charts and graphs. The Chart Wizard provides a tool to simplify the

process of chart construction.

As we saw in Chapter 1b, using Microsoft Excel, it is possible to display data held in a range of spreadsheet cells in

a variety of charts or graphs.

7.1 Creating a histogram

Earlier in this chapter, we looked at data on output and number of employees. We will now use the same data to

illustrate how Excel can be used to create a histogram. The data is first input into a spreadsheet as follows.

A B C D

Weekly output per employee

1087 850 1084 792

924 1226 1012 1205

1265 1028 1230 1182

1086 1130 989 1155

1134 1166 1129 1160

The next step is to calculate the frequencies using the FREQUENCY function. This function calculates how often

values occur within a

range of values, and then returns a vertical array of numbers. Since FREQUENCY returns an

array, it must be entered as an array formula. The format is =FREQUENCY(DATARANGE,BIN) where BIN is the

required range to be used for the x axis. This has been input into cells F3 to F9 in the spreadsheet below.

To enter the FREQUENCY formula, first select the range G3:G9 and then enter =FREQUENCY(A3:D7,F3:F9) and hold

down the CTRL and SHIFT keys as you press ENTER.

A B C D E F G

Weekly output per employee

Output Frequency

1087 850 1084 792 700 0

924 1226 1012 1205 800 1

1265 1028 1230 1182 900 1

1086 1130 989 1155 1000 2

1134 1166 1129 1160 1100 5

1200 7

1300 4

T F

RWAR

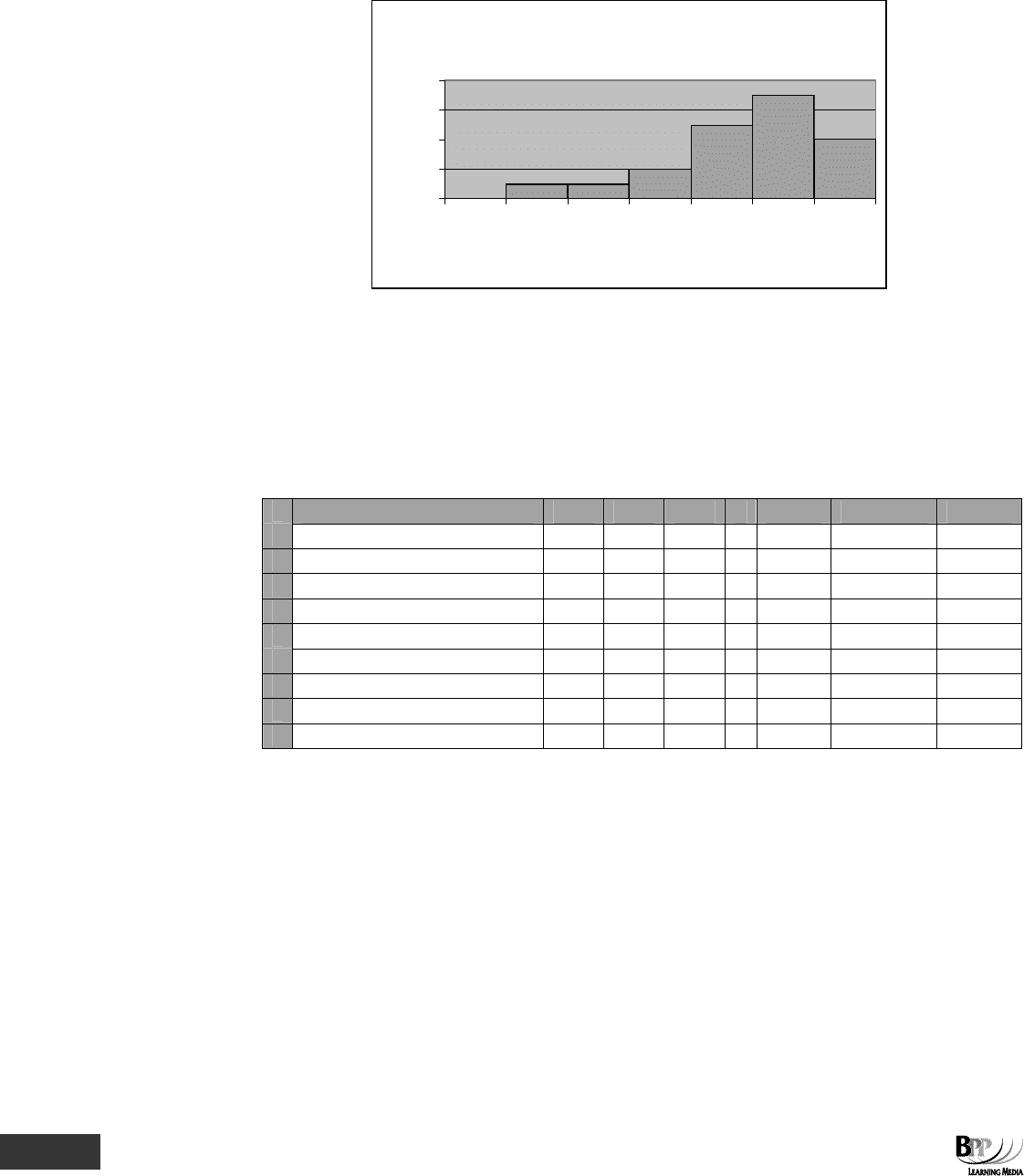
112 3: Data presentation ⏐ Part B Summarising and analysing data

We can now use the Chart Wizard to produce a histogram from the frequency data. Select the range G3:G9 and

click on the chart icon. Select the

column option and then in Step 2 click on the series tab and click in the box next

to 'Category (x) axis labels'. Select the range F3:F9 and click finish.

Frequency distribution

700 800 900 1000 1100 1200 1300

Output

Frequency

In order to make the bars touch, right click on one of the bars on the chart, select FORMAT DATA SERIES, then

OPTIONS. Set the gap width to zero.

7.2 Creating an ogive

Excel can also be used to draw an ogive, the graph of a cumulative frequency distribution. In the spreadsheet

below, a column for

cumulative frequency has been inserted. The cumulative frequencies are calculated by

entering =G3 into cell H3, then =H3+G4 into cell H4. This formula has then been copied down to cell H9.

A B C D E F G H

Weekly output per employee

Output Frequency Cum frq

1087 850 1084 792 700 0 0

924 1226 1012 1205 800 1 1

1265 1028 1230 1182 900 1 2

1086 1130 989 1155 1000 2 4

1134 1166 1129 1160 1100 5 9

1200 7 16

1300 4 20

We can now use the Chart Wizard to produce an ogive using the XY chart option. First select the range F3:F9 then

hold down the CTRL key and select the range H3:H9. Click on the chart icon and select the XY (scatter) with lines

option. Add titles to the chart.

Part B Summarising and analysing data ⏐ 3: Data presentation 113

Ogive

0 500 1000 1500

Output

Cumulative

frequency

Chapter Roundup

• Tables are a simple way of presenting information about two variables.

• Charts often convey the meaning or significance of data more clearly than would a table.

• There are three main types of bar chart: simple, component (including percentage component) and multiple (or

compound).

• Frequency distributions are used if values of particular variables occur more than once.

• A frequency distribution can be represented pictorially by means of a histogram. The number of observations in a

class is represented by the area covered by the bar, rather than by its height.

• An ogive shows the cumulative number of items with a value less than or equal to, or alternatively greater than or

equal to, a certain amount.

• Scatter diagrams are graphs which are used to exhibit data, (rather than equations) in order to compare the way in

which two variables vary with each other.

• Excel includes the facility to produce a range of charts and graphs. The Chart Wizard provides a tool to simplify the

process of chart construction.

114 3: Data presentation ⏐ Part B Summarising and analysing data

Quick Quiz

1 Which of the following is not recommended when producing a table of information?

A Keeping accuracy to a maximum

B Clearly labelling all columns

C Eliminating unnecessary information

D Ordering columns and rows by order of importance and magnitude

2 When selecting a standard width of bar in a histogram you would select the size of the class interval which occurs

most frequently.

True

False F

3 A grouped frequency distribution can be drawn as a(n) histogram/ogive, whereas a cumulative frequency

distribution can be graphed as a(n) ogive/histogram.

4 A scatter diagram has an x axis and a y axis which represent dependent and independent variables as follows.

x axis independent variable

y axis dependent variable

5 Which Excel function can be used to calculate how often values occur within a range of values?

6 In a histogram, one class is ¾ the width of the other classes. If the score in that class is 33, the correct height to

plot on the histogram is

7 A pie chart is used to display the following data:

Sales %

Region A 26

Region B 41

Region C 33

What angle on the pie chart will be used to represent Region C's share of sales?

A 33

B 237.6

C 118.8

D 59.4

8 A cumulative frequency distribution of output of employees is as follows:

Weekly output Cumulative frequency

Units

Less than 150 90

Less than 200 250

Less than 300 310

Less than 400 340

Less than 600 350

How many employees produced more than 200 units?

How many employees produced between 200 and 300 units?

]

[

Part B Summarising and analysing data ⏐ 3: Data presentation 115

Answers to Quick Quiz

1 A Maximising accuracy would make the table too detailed and hard to understand.

2 True

3 A grouped frequency distribution can be drawn as a

histogram, whereas a cumulative frequency distribution can

be graphed as an

ogive.

4 x axis independent variable

y axis dependent variable

5 Frequencies are calculated in Excel using the FREQUENCY function.

0.75

= 44

7 C Region C's angle is given by 33% × 360 = 118.8

8 produced more than 200 units

produced between 200 and 300 units

Now try the questions below from the Exam Question Bank

Question numbers Pages

31-37 330-332

]

[

116 3: Data presentation ⏐ Part B Summarising and analysing data

117

Topic list Syllabus references

1 The arithmetic mean C, (iv), (4)

2 The mode C, (iv), (4)

3 The median C, (iv), (4)

Averages

Introduction

In Chapter 3 we saw how data can be summarised and presented in tabular, chart and

graphical formats. Sometimes you might need more information than that provided by

diagrammatic representations of data. In such circumstances you may need to apply some

sort of numerical analysis, for example you might wish to calculate a measure of centrality

and a measure of dispersion. In Chapter 4b we will look at measures of dispersion, in this

chapter measures of centrality, or averages.

An average is a representative figure that is used to give some impression of the size of all

the items in the population. There are three main types of average.

• Arithmetic mean

• Mode

• Median

We will be looking at each of these averages in turn, their calculation, advantages and

disadvantages. In the next chapter we will move on to the second type of numerical measure,

measures of dispersion.

118 4a: Averages ⏐ Part B Summarising and analysing data

1 The arithmetic mean

1.1 Arithmetic mean of ungrouped data

The arithmetic mean is the best known type of average and is widely understood. It is used for further statistical

analysis.

Arithmetic mean of ungrouped data =

itemsofNumber

itemsofvaluesofSum

The arithmetic mean of a variable x is shown as

('x bar').

1.1.1 Example: The arithmetic mean

The demand for a product on each of 20 days was as follows (in units).

3 12 7 17 3 14 9 6 11 10 1 4 19 7 15 6 9 12 12 8

The arithmetic mean of daily demand is

days of Number

demand of Sum

185

= 9.25 units

In this example, demand on any one day is never actually 9.25 units. The arithmetic mean is merely an

average

representation

of demand on each of the 20 days.

1.2 Arithmetic mean of data in a frequency distribution

It is more likely in an assessment that you will be asked to calculate the arithmetic mean of a frequency

distribution

. In our previous example, the frequency distribution would be shown as follows.

Daily demand

Frequency

Demand

frequency

185

= 9.25

T F

RWAR

Part B Summarising and analysing data ⏐ 4a: Averages 119

1.3 Sigma, Σ

Σ means 'the sum of' and is used as shorthand to mean 'the sum of a set of values'.

In the previous example:

(a)

∑f would mean the sum of all the frequencies, which is 20

(b)

∑fx would mean the sum of all the values of 'frequency multiplied by daily demand', that is, all 14

values of fx, so

∑fx = 185

1.4 Arithmetic mean of grouped data in class intervals

The arithmetic mean of grouped data,

∑

where n is the number of values recorded, or the number

of items measured.

This formula will be given to you in your exam.

You might also be asked to calculate (or at least approximate) the arithmetic mean of a frequency distribution,

where the frequencies are shown in class intervals.

1.4.1 Example: The arithmetic mean of grouped data

Using the example in Paragraph 1.2, the frequency distribution might have been shown as follows.

Daily demand Frequency

> 0 ≤ 5 4

> 5

≤ 10 8

>10

≤ 15 6

>15

≤ 20

There is, of course, an extra difficulty with finding the average now; as the data have been collected into classes, a

certain amount of detail has been lost and the values of the variables to be used in the calculation of the mean are

not clearly specified.

1.4.2 The mid-point of class intervals

To calculate the arithmetic mean of grouped data we therefore need to decide on a value which best represents all

of the values in a particular class interval

. This value is known as the mid-point.

The

mid-point of each class interval is conventionally taken, on the assumption that the frequencies occur evenly

over the class interval range. In the example above, the variable is discrete, so the first class includes 1, 2, 3, 4 and

5, giving a mid-point of 3. With a

continuous variable, the mid-points would have been 2.5, 7.5 and so on. Once

the value of x has been decided, the mean is calculated using the formula for the arithmetic mean of grouped data.

Key term

T F

RWAR

Assessment

formula