CIMA - C3 Fundamentals Of Business Mathematics

Подождите немного. Документ загружается.

140 4b: Dispersion ⏐ Part B Summarising and analysing data

4.6 The main properties of the standard deviation

The standard deviation's main properties are as follows.

(a) It is based on

all the values in the distribution and so is more comprehensive than dispersion

measures based on quartiles, such as the quartile deviation.

(b) It is suitable for

further statistical analysis.

more difficult to understand than some other measures of dispersion.

The importance of the standard deviation lies in its

suitability for further statistical analysis (we shall consider

this further when we study the normal distribution in Chapter 7).

4.7 The variance and the standard deviation of several items together

You may need to calculate the variance and standard deviation for n items together, given the variance and

standard deviation for one item alone.

4.8 Example: Several items together

The daily demand for an item of inventory has a mean of 6 units, with a variance of 4 and a standard deviation of 2

units. Demand on any one day is unaffected by demand on previous days or subsequent days.

Required

Calculate the arithmetic mean, the variance and the standard deviation of demand for a five day week.

Solution

If we let

• Arithmetic mean =

= 6

• Variance = σ

= 4

• Standard deviation = σ= 2

• Number of days in week = n = 5

The following rules apply to

x, σ

and σ when we have several items together.

• Arithmetic mean = n x = 5 × 6 = 30 units

• Variance = nσ

= 5 × 4

= 20 units

• Standard deviation =

nσ = 20 = 4.47 units

5 The coefficient of variation

5.1 Comparing the spreads of two distributions

The spreads of two distributions can be compared using the coefficient of variation.

Coefficient of variation (coefficient of relative spread) =

Standard deviation

mean

Formula to

learn

T F

RWAR

Part B Summarising and analysing data ⏐ 4b: Dispersion 141

The bigger the coefficient of variation, the wider the spread. For example, suppose that two sets of data, A and B,

have the following means and standard deviations.

A B

Mean 120 125

Standard deviation 50 51

Coefficient of variation (50/120) 0.417 (51/125) 0.408

Although B has a higher standard deviation in absolute terms (51 compared to 50) its relative spread is less than

A's since the coefficient of variation is smaller.

Question

Coefficient of variation

Calculate the coefficient of variation of the distribution in the questions on pages 134 and 137.

Answe

Coefficient of variation =

mean

deviation standard

2.32

72.13

= 0.426

Question

Variance

The number of new orders received by five salesmen last week is: 1, 3, 5, 7, 9. The variance of the number of new

orders received is:

A 2.40

B 2.83

C 6.67

D 8.00

Answe

)x (x −

1 16

3 4

5 0

7 4

∑x =

()

xx −∑

x = = 5

()

−∑

= 8

The correct answer is therefore D.

142 4b: Dispersion ⏐ Part B Summarising and analysing data

6 Skewness

6.1 Skewed distributions

As well as being able to calculate the average and spread of a frequency distribution, you should be aware of the

skewness of a distribution.

Skewness is the asymmetry of a frequency distribution curve.

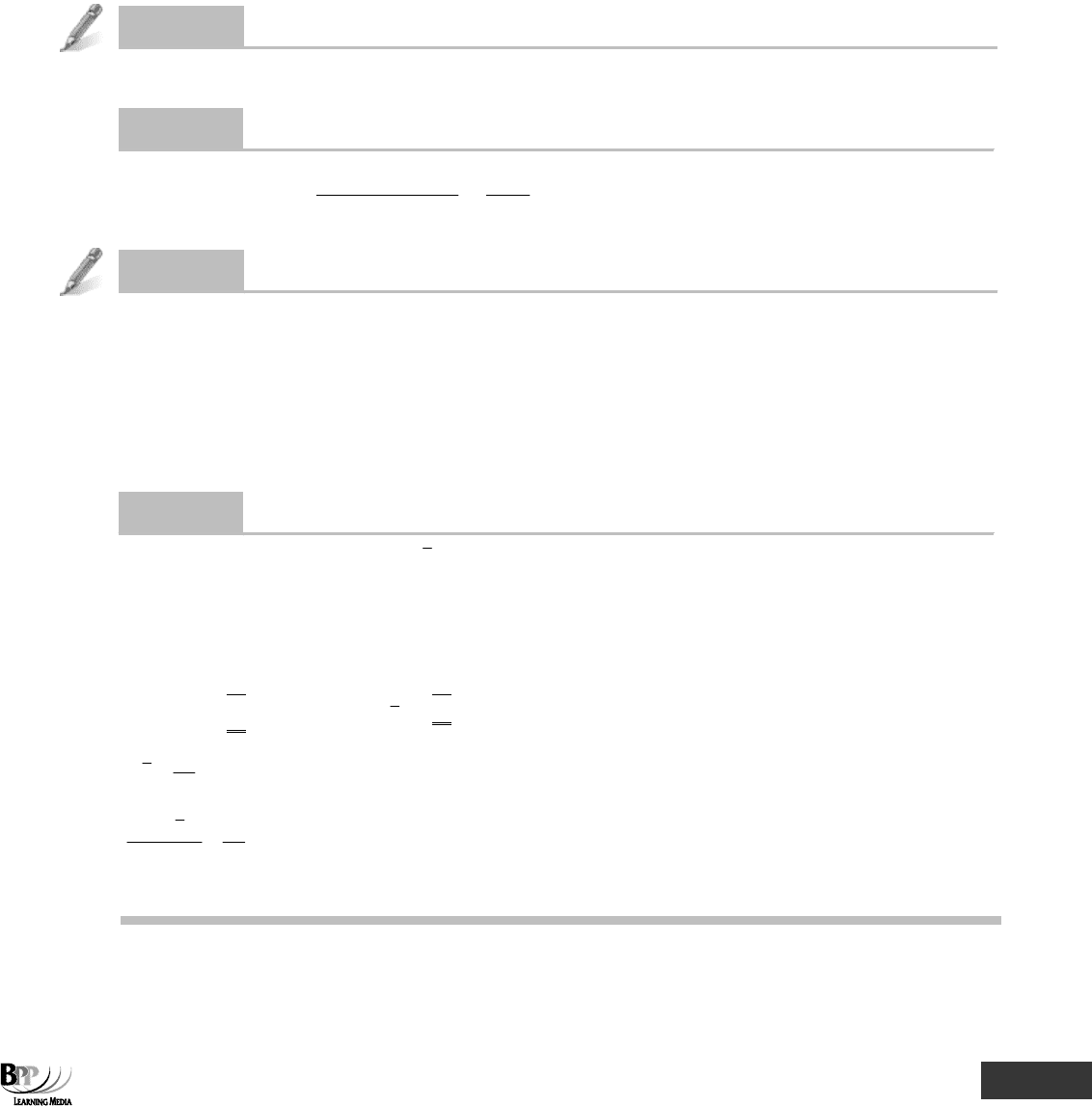
6.2 Symmetrical frequency distributions

A symmetrical frequency distribution (a normal distribution) can be drawn as follows.

Properties of a symmetrical distribution

• Its mean, mode and median all have the same value, M

• Its two halves are mirror images of each other

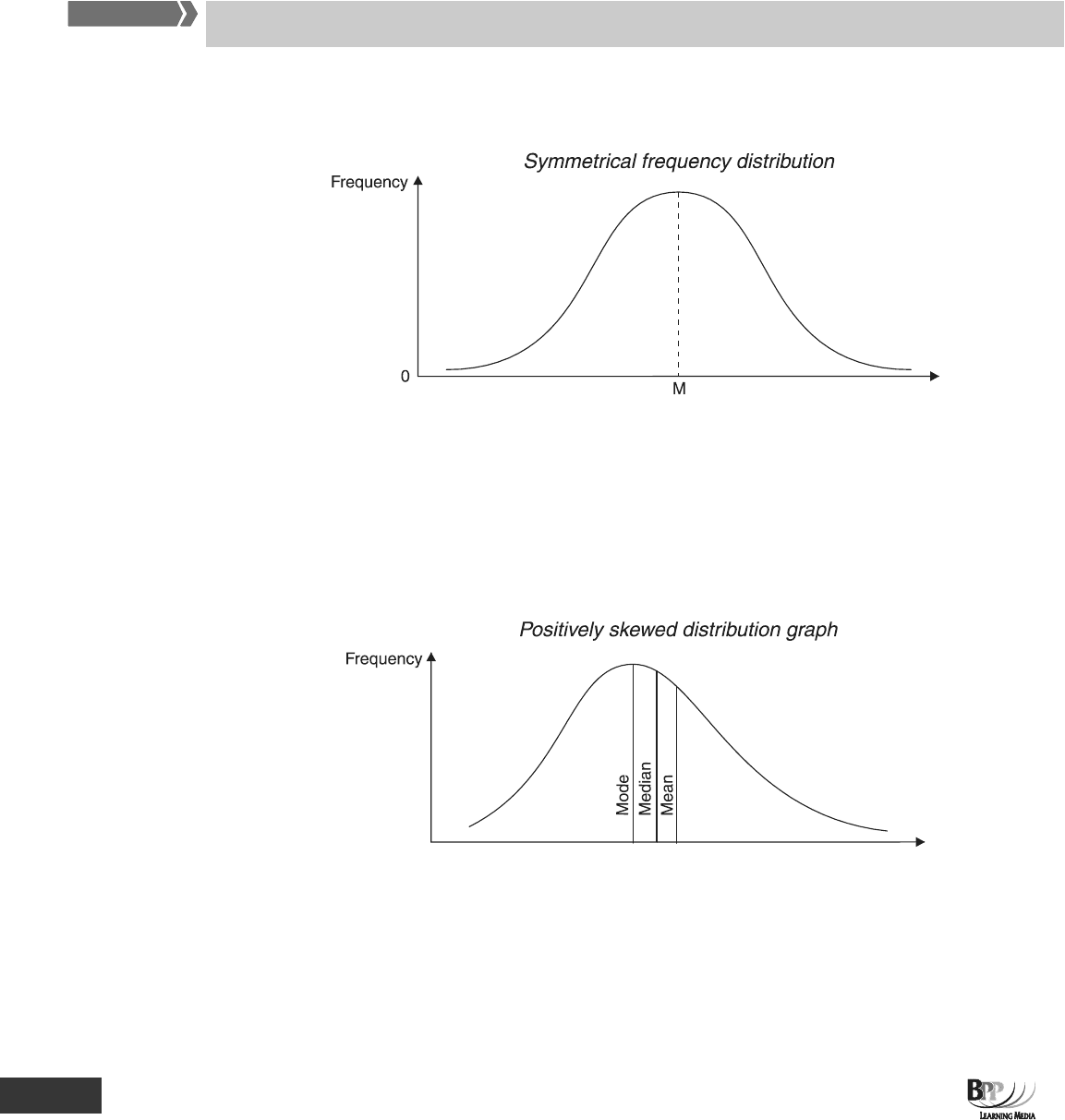
6.3 Positively skewed distributions

A positively skewed distribution's graph will lean towards the left hand side, with a tail stretching out to the right,

and can be drawn as follows.

Properties of a positively skewed distribution

• Its mean, mode and median all have different values

• The mode will have a lower value than the median

• Its mean will have a higher value than the median (and than most of the distribution)

• It does not have two halves which are mirror images of each other

T F

RWAR

Part B Summarising and analysing data ⏐ 4b: Dispersion 143

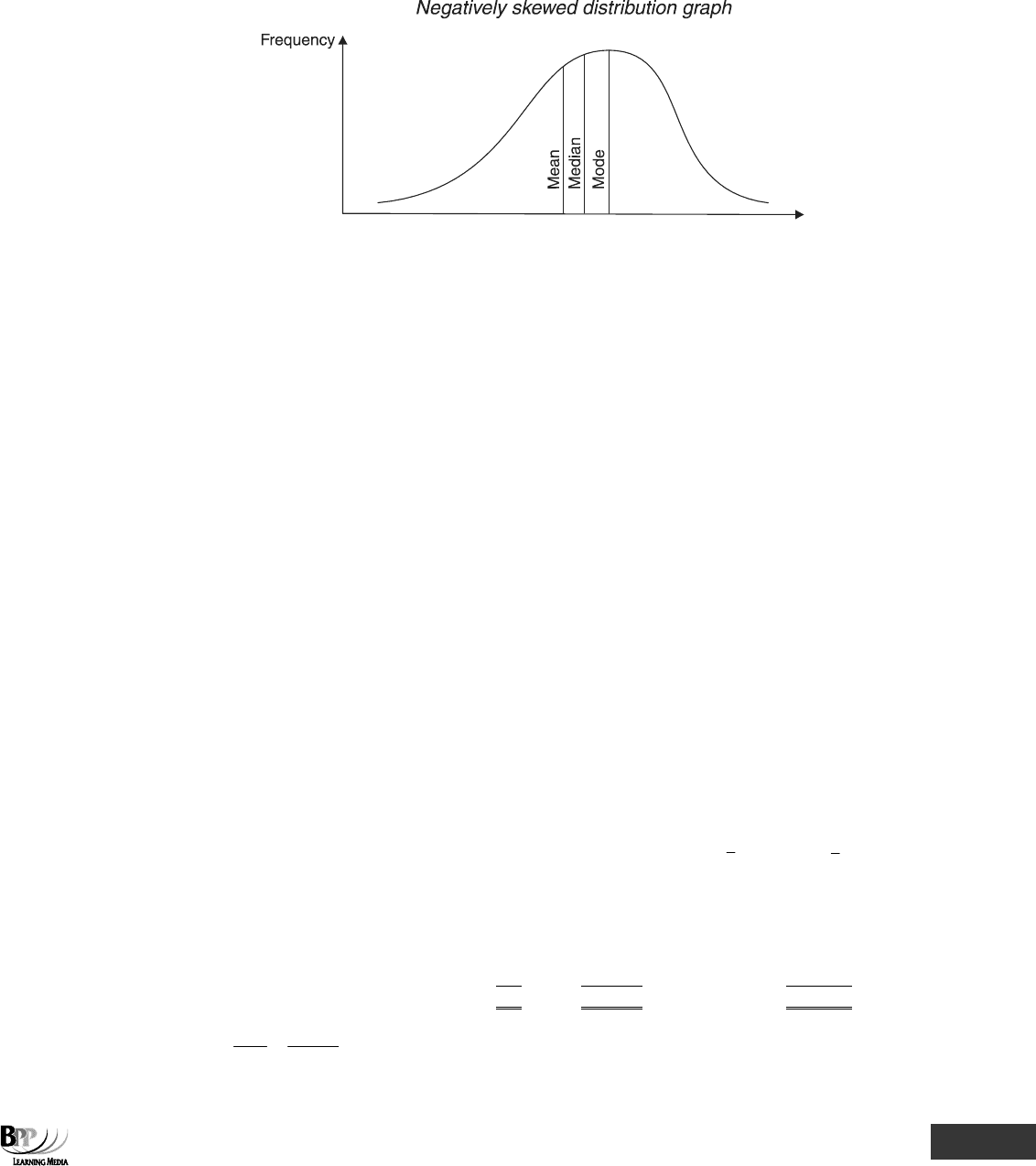
6.4 Negatively skewed distributions

A negatively skewed distribution's graph will lean towards the right hand side, with a tail stretching out to the

left, and can be drawn as follows.

Properties of a negatively skewed distribution

• Its mean, median and mode all have different values

• The mode will be higher than the median

• The mean will have a lower value than the median (and than most of the distribution)

Since the mean is affected by extreme values, it may not be representative of the items in a very skewed

distribution.

6.5 Example: Skewness

In a quality control test, the weights of standard packages were measured to give the following grouped frequency

table.

Weights in grams Number of packages

198 and less than 199 3

199 and less than 200 8

200 and less than 201 93

201 and less than 202 148

202 and less than 203 48

Required

(a) Calculate the mean, standard deviation and median of the weights of the packages.

(b) Explain whether or not you think that the distribution is symmetrical.

Solution

(a) Weight

Mid point

g x f fx

(

)

x-xf

198 and less than 199

198.5

595.5

–2.77

23.0187

199 and less than 200

199.5

1,596.0

–1.77

25.0632

200 and less than 201

200.5

18,646.5

–0.77

55.1397

201 and less than 202

201.5

148

29,822.0

0.23

7.8292

202 and less than 203

202.5

9,720.0

1.23

72.6192

300

60,380.0

183.6700

Mean =

∑

300

380,60

= 201.27g

144 4b: Dispersion ⏐ Part B Summarising and analysing data

Standard deviation =

300

67.183

= 0.78g

The

median (the 150th item) could be estimated as

201 +

148

)3893150( −−−

= 201.31g

(b) The distribution appears not to be symmetrical, but negatively skewed.

The mean is in the higher end of the range of values at 201.27 g.

The median has a higher value than the mean, and the mode has a higher value than the median. This

suggests that the frequency distribution is negatively skewed.

Measures of spread are valuable in giving a full picture of a frequency distribution. We would nearly always want to

be told an average for a distribution, but just one more number, a measure of spread, can be very informative.

Question

Skewness

Which of these options is true where data is highly positively skewed?

A The least representative average is the median

B The mode will overestimate the average

C The mean will tend to overestimate the average

D The mean, mode and median will produce equally representative results

Answe

C The mean will tend to overstate the average, and the mode will underestimate it.

7 Using spreadsheets

Excel can be used to produce descriptive statistics concerning a data set. A range of cells is given a name and

measures of average and dispersion calculated.

7.1 Naming a range of data

In the spreadsheet below, data concerning the times taken to produce a batch of 100 units of Product X have been

input.

A B C D E F

1 Tine taken in minutes to produce a batch of 100 units of Product X

2 21 17 24 11 37 27

3 20 15 17 23 29 30

4 24 18 24 21 24 20

Important!

T F

RWAR

Part B Summarising and analysing data ⏐ 4b: Dispersion 145

The first step is to name the range of data from cell A2 to F4. This is done by selecting the cells to be included,

double clicking in the name box at the top left of the screen to the left of the formula bar, and typing in the name

DATA. This will be quicker than specifying cell ranges for each calculation.

7.2 Measures of average

The measures of average are the mean, mode and median.

A B C D E F

Time taken in minutes to produce a batch of 100 units of Product X

21 17 24 11 37 27

20 15 17 23 29 30

24 18 24 21 24 20

Mean 22.33

Mode 24

Median 22

(a) In cell B6, the mean has been calculated using the AVERAGE function

=AVERAGE(DATA)

(b) In cell B7, the mode has been calculated using the MODE function

=MODE(DATA)

=MEDIAN(DATA)

7.3 Measures of dispersion

The measures of dispersion are the range, standard deviation and variance.

A B C D E F

Time taken in minutes to produce a batch of 100 units of Product X

21 17 24 11 37 27

20 15 17 23 29 30

24 18 24 21 24 20

Minimum 11

Maximum 37

Range 26

Standard deviation 6.06

Variance 36.71

(a) In cell B6, the minimum has been calculated using the MIN function

=MIN(DATA)

(b) In cell B7, the maximum has been calculated using the MAX function

=MAX(DATA)

146 4b: Dispersion ⏐ Part B Summarising and analysing data

=B7-B6

(d) In cell B9, the standard deviation has been calculated using the STDEV function

=STDEV(DATA)

(e) In cell B10, the variance been calculated using the VAR function

=VAR(DATA)

You need to learn how to put these functions into an Excel formula so that you can reproduce them in the

assessment.

Chapter Roundup

• The range is the difference between the highest and lowest observations.

• The quartiles and the median divide the population into four groups of equal size.

• The semi-interquartile range is half the difference between the upper and lower quartiles.

• The inter-quartile range is the difference between the upper and lower quartiles (Q

– Q

) and hence shows the

range of values of the middle half of the population.

• The mean deviation is a measure of the average amount by which the values in a distribution differ from the

arithmetic mean.

• The variance, σ

, is the average of the squared mean deviation for each value in a distribution.

• The standard deviation, which is the square root of the variance, is the most important measure of spread used in

statistics. Make sure you understand how to calculate the standard deviation of a set of data.

• The spreads of two distributions can be compared using the coefficient of variation.

• Skewness is the asymmetry of a frequency distribution curve.

• Excel can be used to produce descriptive statistics concerning a data set. A range of cells is given a name and

measures of average and dispersion calculated.

Quick Quiz

1 Fill in the blanks in the statements below using the words in the box.

(a) quartile = Q

= value which 25% of the population fall.

(b) quartile = Q

= value which 25% of the population fall.

Upper Above Below Lower

2 (a) The formula for the semi-interquartile range is

(b) The semi-interquartile range is also known as the

Assessment

focus point

Part B Summarising and analysing data ⏐ 4b: Dispersion 147

3 Which command should be entered into a cell to find the mean of a number of values labelled DATA in an Excel

spreadsheet?

4 In a negatively skewed distribution:

A The mean is the same as the median

B The mean is smaller than the median

C The mean lies between the median and the mode

D The mean is larger than the median

5 The standard deviation of a sample of data is 36. What is the value of the variance?

Answers to Quick Quiz

1 (a) Lower quartile = Q

= value below which 25% of the population fall

(b)

Upper quartile = Q

= value above which 25% of the population fall

2 (a)

−

(b) Quartile deviation

3 =AVERAGE(DATA)

4 B The mean is smaller than the median.

5 The variance is the square of the standard deviation.

= 1,296

Now try the questions below from the Exam Question Bank

Question numbers Pages

43-45 333-334

1,296

148 4b: Dispersion ⏐ Part B Summarising and analysing data

149

Topic list Syllabus references

1 Basic terminology C, (viii), (7)

2 Index relatives C, (viii), (7)

3 Time series of index relatives C, (viii), (7)

4 Time series deflation C, (x), (7)

5 Composite index numbers C, (viii), (7)

6 Weighted index numbers C, (ix), (7)

7 The Retail Prices Index for the United Kingdom C, (xiii), (x), (7)

Index numbers

Introduction

A number of methods of data presentation looked at in Chapter 3 can be used to identify

visually the trends in data over a period of time. It may also be useful, however, to identify

trends using statistical rather than visual means. This is frequently achieved by constructing

a set of index numbers.

Index numbers provide a standardised way of comparing the values, over time, of prices,

wages, volume of output and so on. They are used extensively in business, government and

commerce.