Чураков Е.П. Математические методы обработки экспериментальных данных в экономике

Подождите немного. Документ загружается.

Пусть z

В^, yeR^ и z -

(p(y) —

решение некоторой задачи,

найденное как функция вектора

у.

Тогда:

Определение

2.3.

Решение z =

фС^)

Hдiзыв2icтcя

устойчивым,

ес-

ли при

V8 > О

35(8)

> О

такое,

что из неравенства

\\у\

—

У2\\

< 5(e)

сле-

дует ||zi -

Z2II

< е, где у\ и

У2 —

произвольные элементы из R'^,

Z]=(f(y\),Z2='(p(y2)'

По существу, это определение означает, что решение устойчи-

во,

если малым по норме изменениям

8у

аргумента

соответству-

ют

малые по норме изменения

8z в

решении

так что ||8z||~>0 при

IISjiHO.

Определение 2.4. Задача поиска решения z = ф(у) называется

корректно

поставленной на паре пространств R'^, R'", если вы-

полняются условия:

для \/уе

Я^

существует решение ze R'";

2) решение определено однозначно,

т.е.

единственно;

3) решение устойчиво.

Задачи, не удовлетворяющие перечисленным требованиям,

называют

некорректно

поставленными.

связи с поиском МНК-

оценок наибольшее беспокойство вызывает третье условие, что и

порождает, как

уже

отмечалось, необходимость найти своеобраз-

ный критерий устойчивости решения. Осуществим это намере-

ние в связи с поиском решения системы алгебраических уравне-

ний

y=-Az,AER'''^, (2.41)

подобной определяющей МНК-оценку системе (2.23). Для этого

нам понадобятся некоторые дополнительные сведения о вектор-

ных

матричных нормах.

Определение

2.5.

Пустъу=

[J/]GR'^,

т.е.

2,...,

п.

Тогда

чис-

ло

М = (ly/+ ЬГ

... +

\УпГ)'^^Р>и

(2.42)

называется

гельдеровой

нормой вектора у.

зависимости

от/?

получают

ту

или

иную

частную норму Так,

при/7 = 1 получают октаэдрическую [9], или /i-норму [26]; при

имеем уже широко нами использовавшуюся евклидову, или

/2-норму; при /7 = оо получим кубическую, или /оо-норму

|[у||

= maxjlyj, / =

1,2,...,

п).

зависимости от характера решаемой

задачи применяют ту или иную частную норму.

Определение 2.6.

Пусть А

[а,у]е

R'"^ и

\\у\\е

R^.

Тогда число

;;GR^з;^0„

А'II

называется

нормой матрицы

А,

согласованной

нормой вектора;?.

Помимо трех традиционных аксиом, которым удовлетворяет

норма любого математического объекта из линейного простран-

ства, матричная норма (2.43) обладает еще одним свойством: ес-

лиАеК'^'^иВеК"'^,то

|И^|<|И1|хМ.

(2.44)

зависимости от способа определения векторной нормы по-

лучают определенную матричную норму Так, если

\\у\\

- /i-нор-

ма, то

М||=тахЕ|%|

1<А:<л/=:1

И называется максимальной

столбцовой

нормой. Если ||у|| -

/оо-норма, то

М||=тах

\а^1,\

\<i<mk=\

называется максимальной

строчной

нормой. Если Щ

—

евкли-

дова норма, то

MlhV^max»

где Хтах

- максимальное собственное число матрицы

А^А

назы-

вается

спектральной

нормой. Используются и другие матричные

нормы. Например,

т п ^

MJhJX

Y^afj,

илиприт =

А/

\\А\\=п

max \ац,\,

V/=U=1 \<i,k<n

Полезно иметь в виду

\\Щ >

|И"^||

l|J£ll/IMI,

где

Е,

Ае R^^^

Возвратимся теперь к системе (2.41). Пусть вместо точного

значения у получено приближенное значение у

у + 5у. Тогда

вместо точного решения z системы получим приближенное

z= z + 6z, причем отклонения связаны уравнением

Ьу

Adz

или

5z = ^~^б>^. Переходя к нормам, получаем с учетом (2.44)

||5г|| ^

|И~^11 X

1|5у|1- Рассмотрим относительную ошибку решения

||Sz||/||zl|. Из (2.44) следует

||j;

|| <

\\А\\

х ||/||. Перемножив два послед-

них неравенства, получим

NIxllFll^lNlxIM-'llxIMilxllzlH

45)

=>W/||z1|:S|H-4|x|MI|x||5j;||/|ly'||.

Отсюда следует, что относительная ошибка в решении, вы-

званная неточным заданием входных данных

j;*,

тем больше, чем

больше число

ЦА'^Ц

\\A\l

которое может служить своеобразным

индикатором устойчивости решения.

Определение 2.7. Число D^ =

Ы~Ч

1И11

Для невырожденной

матрицы ^ и

оо для

вырожденной называется

числом

обуслов-

ленности

матрицы А.

Некоторые характерные свойства числа обусловленности [19]:

max!

l^minl"~

наибольшее

Наи-

меньшее по модулю собственные числа матрицы

А;

D^B

D^D^

для произведения АВ матриц. Матрицы с большим числом обус-

ловленности называются

плохо обусловленными

в противовес хо-

рошо

обусловленным

матрицам, которым соответствуют малые

числа обусловленности.

Таким образом, чем больше число обусловленности матрицы,

тем большая относительная ошибка решения порождается одной

и той же

относительной ошибкой задания входных данных

>?.

При

этом следует иметь в виду, что конкретное значение числа обус-

ловленности зависит от способа задания нормы

\\А\\

матрицы А,

Заметим, что современные пакеты прикладных программ преду-

сматривают вычисление чисел обусловленности матриц при раз-

личных заданиях их норм.

Выявленные особенности системы (2.41) свойственны, разу-

меется, и системе (2.23), используемой для поиска МНК-оценки

(2.24).

Если матрица Т Т оказывается плохо обусловленной, ис-

пользовать выражение (2.24) как средство практического вычис-

ления МНК-оценки рискованно, так как даже малые ошибки в

задании вектора

Ч^^у

могут привести к большим отклонениям ре-

шения, т.е. к большим ошибкам МНК-оценки. Несложно полу-

чить аналогичное (2.45) неравенство для уравнения (2.23). Пусть

У*

\ff^Q __

гипотетический вектор экспериментальных данных,

соответствующих идеальному случаю безошибочных наблюде-

ний,

= Y^e + 8

—

результат реальных наблюдений. Тогда

по

аналогии

(2.45) получаем

не

в||

||в||

l^'^^'ll

||(W)-^||

{^''eW

II^^Vll.

Отсюда следует,

что при

плохо обусловленной матрице

Y^Y

нужны иные, нежели (2.24), принципы поиска решения системы

(2.23).

Эти

принципы

и при

плохо обусловленной матрице

Y^Y

должны гарантировать приемлемо малые ошибки оценивания.

Успехи вычислительной математики

этом направлении

в по-

следнее время связаны с разработкой так называемых .we/wc?(3oe/?^-

гуляризации, объединенных

весьма разветвленную математиче-

скую теорию решения некорректных задач (например, [24]).

Да-

лее,

не

вдаваясь

терминологические

принципиальные осо-

бенности методов регуляризации, рассмотрим один

из

алгорит-

мов,

позволяющих обеспечить устойчивость решения при вычис-

лении МНК-оценок

организовать достаточно рациональную

вычислительную схему поиска этих оценок.

2.3.7. Рекуррентный метод наименьших квадратов

Предположим,

что

поиск МНК-оценки осуществляется

не по

всему массиву

>^1,

yj-,

'•••>Уп

экспериментальных

данньис,

а лишь

по

части^1,^2»

•••»

Уь

к<п.

Это означает, что целевая функция (2.20)

и соответствующая оптимизационная задача приобретают вид

/jt

= X

[У]

W^(xj)ef

min

по е.

(2.46)

Техника решения задачи (2.46) уже известна, и ее «материали-

зация» может быть представлена

форме (2.25)

в^^>

lv(xi)yr

(2.47)

Здесь индекс

оценки указывает

на

объем эксперименталь-

ных данных, используемых при ее вычислении. Выражение (2.47)

введено чисто формально

том отношении, что проблема обра-

щаемости матрицы в (2.47) не обсуждается, так как в последую-

щем она легко снимается.

Утверждение 2.9. Пусть матрицы Р, Q, R таковы, что образуют

невырожденную матрицу

Р~^ 4-

Q^RT^Q.

Тогда справедливо пред-

ставление

(Р-*

Q^R-^Q)-^

=Р-

PQ^iQPQ^

+ Ry^QP. (2.48)

Доказательство этой так называемой леммы об

обращении

ма-

трицы можно найти, например, в [20], и мы не будем на нем ос-

танавливаться.

Введем обозначение

51^

^-l

Ev(^/)v

(^/)

к-\

1 V(^/)V

(Xi) +

V(XA:)¥ (Xk)

-1

ё^^^=щ

= (%-i~^+Wk)V(x,)rK

Воспользовавшись леммой об обращении матрицы, предста-

вим

% = %-1 - '3ik.Mxk)(W^(xj,) 3if,_Mxk) + l)~V(Xk) ^k~h (2.49)

Это позволяет следующим образом преобразовать выражение

(2.47):

fk-i ]

lw(Xi)yi-^\V(xk)yk

к-\

i^k-l -Qk-l^-l) 1 WiXi)yi+^kW(Xj,)yk,

/=l

где обозначено ^^_i = 9l^_iV(X)t)(\|f^(x^) 3ik-Mxk) + l)"V^(^it).

По аналогии с (2.47)

^k-ilv(Xi)yi^e^^-^^

и, следовательно,

в(к) = в<^-^> - ^,_1 в(^-^> +

%^(Хк)Ук^

в соответствии с введенными обозначениями имеем:

Sik-Г^

91^-^

yif(Xk)yv^(Xk) => Qk-i

= ^к

У¥(хк)У¥^{Хк).

Это позволяет окончательно записать

в(к) = в^^-1)^ 9i;t W(Xk)(yk- V(Xk)e^^-'^), k=h2,..., п. (2.50)

Совокупность выражений (2.49), (2.50) обычно и принято на-

зывать рекуррентным методом наименьших квадратов (РМНК).

Вычисления по этому методу организуются последовательно.

Вначале полагают к= I; задают начальные условия, наиболее ча-

сто в виде 9^^^ = 0,91о = уД где

= const >>

из (2.49) находят 9li,

а из (2.50)

—

в^^\ что формально соответствует поиску оценки

в^^^

регрессионных параметров по единственному эксперимен-

тальному результату;;!. Разумеется, никакого серьезного внима-

ния к оценке в^^^ проявлять нельзя, она лишена какого-либо

практического смысла и должна рассматриваться как формаль-

ный «эпизод» на пути получения МНК-оценки. Далее принима-

ют

А:

= 2, из (2.49) находят

912 »

^ из (2.50)

—

в^^\ что соответству-

ет уточненной по второму экспериментальному наблюдению

У2

оценке. Далее аналогичным образом проводятся вычисления при

/: = 3,4,..., л, что приводит к оценке в^'^^ принимаемой за МНК-

оценку.

Как видно, при такой схеме вычислений не приходится обра-

щать плохо обусловленную матрицу, что стимулирует получение

устойчивого решения. Чтобы более явно раскрыть механизм это-

го явления, поступим следующим образом. С использованием

матрицы

91;^

МНК-оценку (2.25) можем представить в следующем

виде:

Е V(Xi)yi

= 91„

yv(Xi)yi.

(2.51)

(=1

/=1

Матрица

91„

вычисляется последовательно. Будем иметь:

% = (%Г^

v(jc,)v^(xi))-'; 9l2 =

(91,-'

Щх2)у/^(Х2)Г^

= (91о-' + v(aci)\|fVi) + W2)v\x2)r^;...;

Если учесть результат последовательного вычисления матри-

цы

91;^,

выражение (2.51) перепишется так:

f . \

-1

1=1

^ 1 " Т ^

Ч '=1 /

-1

(2.52)

/=1

Как видим, оценки (2.51), (2.52) различаются: если в (2.51)

т ^ т

матрица ^ ^=E¥(J^/)V (^/) плохо обусловлена, то ее аналог

/=1

-1 '^ Т -1

V^"

S ¥(^/)¥ (^/) в (2.52) благодаря начальному

условию у

может оказаться хорошо обусловленной матрицей, что и обеспе-

чивает устойчивость решения.

Чтобы получить представление об эффективности РМНК,

приведем результаты одного вычислительного эксперимента. Его

существо заключается в следующем. Были заданы конкретные

матрица Y размерностью

= 10на/г7 + 1=3и вектор в. Матри-

ца Т строилась случайным образом, но так, что один из ее столб-

цов отличался от соседнего только одним элементом, изменение

которого позволяло варьировать число обусловленности матри-

цы

Y^Y.

Далее решалась прямая задача,

результате чего находи-

ли

вектор

j;*

= ^в. Этот вектор искажался случайным «шумом» е

с независимыми и равномерно распределенными на [-с, с] ком-

понентами, что приводило к формированию вектора у - у

г.

Построенный таким образом вектор у использовался при реше-

нии обратной задачи, т.е. при поиске оценки в вектора в в соот-

ветствии с регулярным (2.24) и рекуррентным (2.49), (2.50) мето-

дами наименьших

квадратов.

Результаты вычислений содержатся

табл.

2.1.

таблице использованы следующие обозначения: D =

ЦЧ'^Ч?!!

т -1 т Цф'^еИ

||(^

40 II - число обусловленности матрицы Ч? Т; " ^ " -

llwVll

относительная ошибка при формировании свободных членов

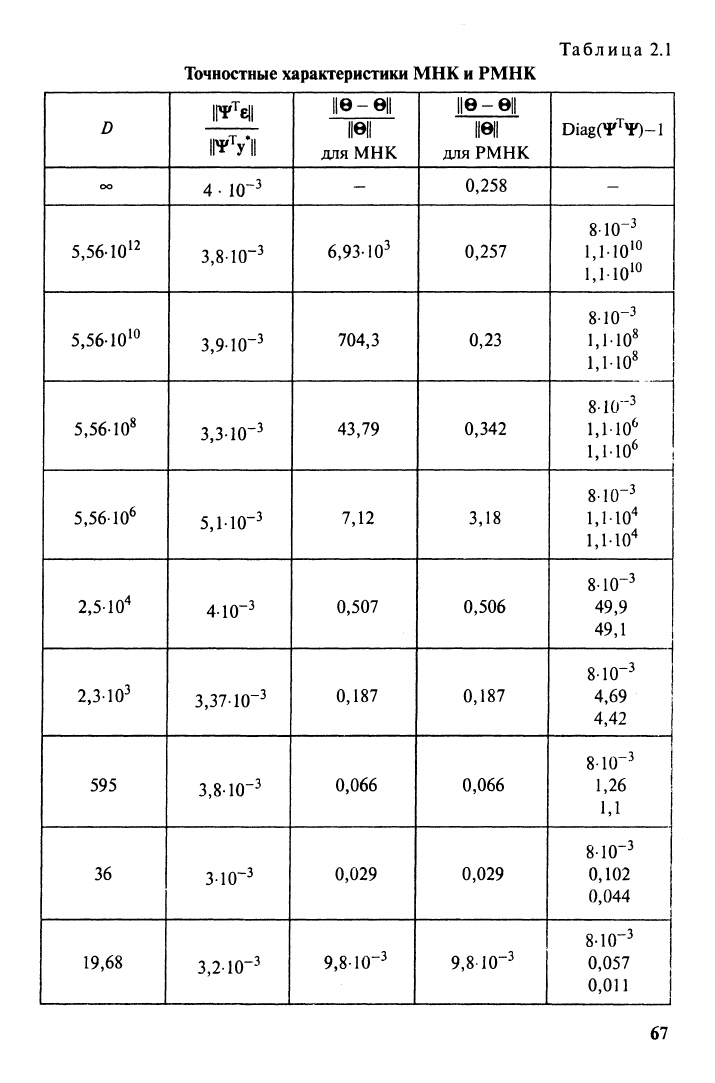
Таблица 2.1

Точностные характеристики МНК

РМНК

оо

5,56-10^2

5,56-10^^

5,56-10^

5,5610^

2,5-10'^

2,310^

595

36 i

' 19,68

II^Vll

•

iO~^

3,810-^

3,910"^

3,310"^

5,110"^

410-^

3,37-10"^

3,8-10"^

310-^

3,210-^

1 1|в-в||

lieil

для МНК

6,9310^

704,3

43,79

7,12

0,507

0,187

0,066

0,029

9,810-^

1 1|в-в||

lieil

1 для РМНК

0,258

0,257

0,23

0,342

3,18

0,506

0,187

0,066

0,029

9,810-^

Diag(y'^^-1

810-^

1,110^^

1,М0^^

8-10-^

1,М0^

' 8-10"^

1,110^

1,110^ 1

8-10""^

1,Ы0^

8-10-^

49,9

49,1 1

8-10-^ j

4,69

4,42

810-^

1,26 1

1,1

8-10-^

0,102

0,044 1

8-10"^

0,057 1

0,011 i

||е~е||

системы уравнений (2.23); ц^., для МНК - относительная

11^11

ошибка МНК-оценки (2.24); ^*

для РМНК - относитель-

II в II

пая ошибка оценки, найденной рекуррентным методом наи-

меньших квадратов-diag

(4f^W)~^

—

столбец диагональных эле-

ментов матрицы (Т Т)~^ определяющей точность МНК-оцен-

ки.

При проведении вычислений применялись евклидова вектор-

ная и спектральная матричная нормы. Содержащиеся в табл. 2.1

данные получены усреднением по десяти реализациям вектора е,

ковариационная матрица которого в эксперименте принималась

равной (2/3)xlO""^jE'. Истинное значение вектора в формирова-

лось случайным образом и оказалось равным в^ = [4,063

0,053

1,655].

Первая строка

табл.

2.1 соответствует вырожденной мат-

рице

4f^4f.

Из таблицы видно, что при плохо обусловленных мат-

рицах

4f^4f

рекуррентный метод, в отличие от регулярного, ведет

себя вполне «пристойно».

По мере уменьшения числа обусловленности матрицы Y^Y

точностные характеристики методов сближаются. Наблюдаемое

ухудшение точности рекуррентного метода в «среднем» диапазо-

не чисел обусловленности можно объяснить

тем,

что все исследо-

вания проводились при одном и том же значении параметра у,

определяющего начальную матрицу ^Q = уЕ в структуре рекур-

рентного алгоритма (было принято у = 10 ). Вместе с тем иссле-

дования свидетельствуют об определенной чувствительности ал-

горитма к значению этого параметра, которое полезно адаптиро-

вать к числу обусловленности матрицы Y^Y. Так, если при

= 5,56

10 положить

10^,

то относительная ошибка рекур-

рентно найденной оценки оказывается равной

0,723

(вместо 3,18

при

10"^).

Выбор оптимального значения параметра

здесь не

обсуждается.

2.3.8. Коэффициент детерминации.

Послерегрессионный анализ регрессионной модели

Коэффициент детерминации. Рассмотренные выше методы рег-

рессионного анализа предполагали, что регрессионная модель

(2.2) (число и характер экзогенных переменных, структура и раз-

мерность вектор-функции Щх) и т.п.) выбрана и обоснована

средствами предварительного анализа регрессионной модели

(см.

п.

1.5). После проведения рефессионного анализа исследова-

тель располагает большей информацией о свойствах модели, так

как для регрессионных параметров модели и дисперсии экспери-

ментальных ошибок получены МНК-оценки и установлены их

основные свойства. Это позволяет с позиций новых знаний еще

раз возвратиться к модели (2.2), подвергнуть ее дополнительному

анализу и при необходимости подкорректировать.

В эконометрических задачах существенная часть послерег-

рессионного анализа связана с применением так называемого

коэффициента детерминации. Чтобы его определить (здесь воз-

можны различные подходы), рассмотрим вариацию (разброс)

вар(у) экспериментальных данных (2.4) относительно их средне-

го значения, которую по определению примем равной

1« -.7 \ -91 -Т

eap{y)

-^(yi-yY ^-Wy-ysW ^-i.y-ys) {y-ys),

rii^i n n

где y=^iyi,

5 = [1

1 ... if GR^

Введем обозначения: /= Тв - оцененные значения регрес-

сионных составляющих в наблюдениях у, г= у —/ есть оценки

экспериментальных ошибок, и представим

1 - - -> т - - -

вар{у)

= '-'{у

- f

f - ysy {у - f

-v

f - ys)

-(y-ff(y-f)-^'(f-ysf(f-ys)

^iy-ff(f-ys)=^

n n n

1 ~ 2 - ^^-^^^

~e'^e

ea/7(/)

-e^(/->;s),

n n

1 - - T -^ -

где величина eap(f)

—(f-ys) (f-ys) характеризует разброс

регрессионных составляющих наблюдений относительно средне-

го значения наблюдений. Покажем, что последнее слагаемое в

(2.53) равно нулю. Действительно, имеем:

ё = д;-Ч'в = ^в

е- '¥(4f^4fy^4f^(We + е) = (£ - WCP^W)-^W^)E.