Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


Appendix 1
Preliminaries (review of
fundamental concepts)
This appendix is for those readers who need a review; a number of fundamental
concepts or theorem will be reviewed without giving proofs or attempting to
achieve completeness.
We assume that the reader is alrea dy familiar with the classes of real
numbers used in analysis. The set of positive integers (also known as natural
numbers) 1, 2, ...; n admits the ope rations of addition without restriction, that
is, they can be added (and therefore multiplied) together to give other positive
integers. The set of integers 0, 1; 2; ...; n admits the operations of addition
and subtraction among themselves. Rational numbers are numbers of the form
p=q, where p and q are integers and q 6 0. Examples of rational numbers are 2/3,
ÿ10=7. This set admits the further property of division among its members. The
set of irrational numbers includes all numbers which cannot be expressed as the
quotient of two integers. Examples of irrational numbers are
2
p
;
11
3
p
; and any
number of the form
a=b
n
p
, where a and b are integers which are perfect nth
powers.
The set of real numbers contains all the rationals and irrationals. The important
property of the set of real numbers fxg is that it can be put into (1:1) cor-
respondence with the set of points fPg of a line as indicated in Fig. A.1.
The basic rules governing the combinations of real numbers are:
commutative law: a b b a; a b b a;
associative law: a b ca bc; a b ca bc;
distributive law: a b ca b a c;
index law a
m
a
n
a
mn
; a
m
=a
n
a
mÿn
a 6 0;
where a; b; c, are algebraic symbols for the real numbers.
Problem A1.1
Prove that
2
p
is an irrational number.
506

(Hint: Assume the contrary, that is, assume that
2
p
p=q, where p and q are
positive integers having no common integer factor.)
Inequalities
If x and y are real numbers, x > y means that x is greater than y;andx < y means
that x is less than y. Similarly, x y implies that x is either greater than or equal
to y. The following basic rules governing the operations with inequalities:
(1) Multiplication by a constant: If x > y, then ax > ay if a is a positive num-
ber, and ax < ay if a is a negative number.
(2) Addition of inequalities: If x; y; u; v are real numbers, and if x > y, and
u > v, than x u > y v.
(3) Subtraction of inequalities: If x > y,andu > v, we cannot deduce that
x ÿ u > y ÿ v. Why? It is evident that x ÿ uÿy ÿ v
x ÿ yÿu ÿ v is not necessarily positive.
(4) Multiplication of inequalities: If x > y, and u > v, and x; y; u; v are all posi-
tive, then xu > yv. When some of the numbers are negative, then the result is
not necessarily true.
(5) Division of inequalities: x > y and u > v do not imply x= u > y=v.
When we wish to consider the numerical value of the variable x without regard
to its sign, we write jxj and read this as `absolute or mod x'. Thus the inequality
jxja is equivalent to a x a.
Problem A1.2
Find the values of x which satisfy the following inequalities:
(a) x
3
ÿ 7x
2
21x ÿ 27 > 0,
(b) j7 ÿ 3xj < 2,
(c)
5
5x ÿ 1
>
2
2x 1
. (Warning: cross multiplying is not permitted.)
Problem A1.3
If a
1
; a
2
; ...; a
n
and b
1
; b
2
; ...; b
n
are any real numbers, prove Schwarz's
inequality:
a
1
b
1
a
2
b
2
a
n
b
n
2
a
2
1
a
2
2
a
n
n
b
2
1
b
2
2
b
n
n
:
507
INEQUALITIES
Figure A1.1.

Problem A1.4
Show that
1
2
1
4
1
8
1
2
nÿ1
1 for all positive integers n > 1:
If x
1
; x
2
; ...; x
n
are n positive numb ers, their arithmetic mean is de®n ed by
A
1
n
X
n
k1
x
k
x
1
x
2
x
n
n
and their geometric mean by
G
n
Y
n
k1
x
k
s
x
1
x
2
x
n
n
p
;
where
P
and
Q
are the summation and product signs. The harmonic mean H is
sometimes useful and it is de®ned by
1
H
1
n
X
n
k1
1
x
k
1
n
1
x
1
1
x
2
1
x
n
:
There is a basic inequality among the three means: A G H, the equality sign
occurring when x
1
x
2
x
n
.
Problem A1.5
If x
1
and x
2
are two positive numbers, show that A G H.
Functions
We assume that the reader is familiar with the concept of functions and the
process of graphing functions.
A polynomial of degree n is a function of the form
f xp
n
xa
0
x
n
a
1
x
nÿ1
a
2
x
nÿ2
a
n
a
j
constant; a
0
6 0:
A polynomial can be diÿerentiated and integrated. Although we have written
a
j
constant, they might still be functions of some other variable independent
of x. For example,
t
ÿ3
x
3
sin tx
2
t
p
x t
is a polynomial functi on of x (of degree 3) and each of the as is a function of a
certain varia ble t: a
0
t
ÿ3
; a
1
sin t; a
2
t
1=2
; a
3
t.
The polynomial equation f x0 has exactly n roots provided we count repe-
titions. For example, x
3
ÿ 3x
2
3x ÿ 1 0 can be written x ÿ 1
3
0 so that
the three roots are 1, 1, 1. Note that here we have used the binomial theorem
a x
n
a
n
na
nÿ1
x
nn ÿ 1
2!
a
nÿ2
x
2
x
n
:
508
APPENDIX 1 PRELIMINARIES
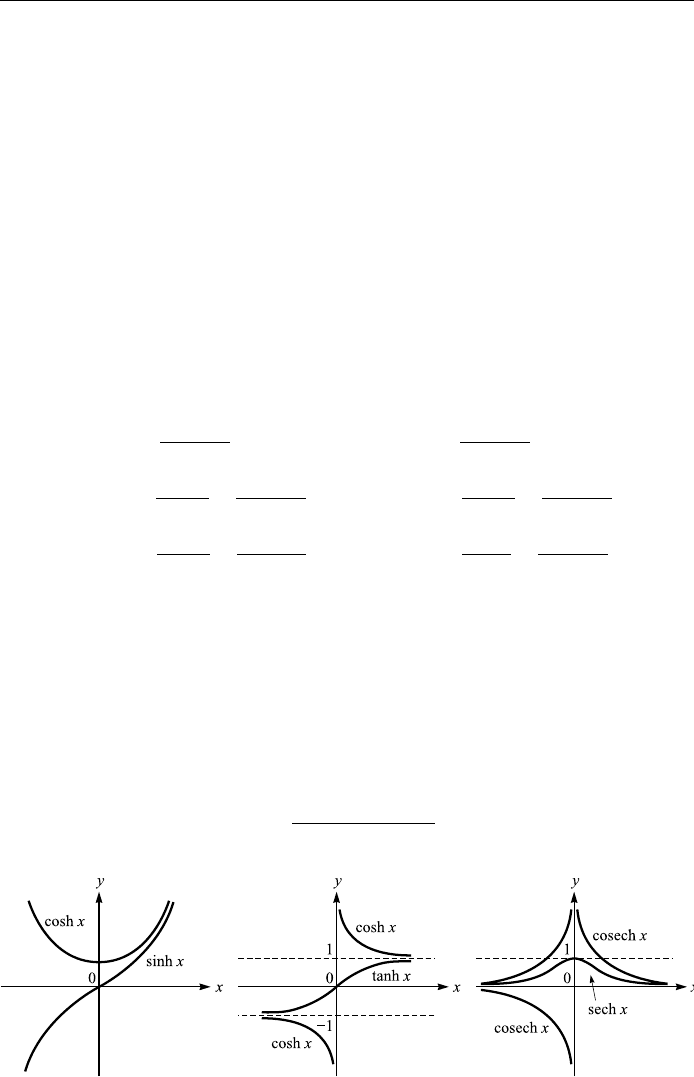
A rational function is of the form f xp
n
x=q
n
x, where p
n
x and q
n
x
are polynomials.
A transcendental function is any function which is not algebraic, for example,
the trigonometric functions sin x, cos x, etc., the exponential functions e
x
, the
logarithmic functions log x, and the hyperbolic functions sinh x, cosh x, etc.
The exponential functions obey the index law. The logarithmic functions are
inverses of the exponential functions, that is, if a
x
y then x log
a
y, where a is
called the base of the logarithm. If a e, which is often called the natural base of
logarithms, we denote log
e
x by ln x, called the natural logarithm of x. The funda-
mental rules obeyed by logarithms are
lnmnln m ln n; lnm=nln m ÿ ln n; and ln m
p
p ln m:
The hyperbolic functions are de®ned in terms of exponential functions as
follows
sinh x
e
x
ÿ e
ÿx
2
; cosh x
e
x
e
ÿx
2
;
tanh x
sinh x
cosh x
e
x
ÿ e
ÿx
e
x
e
x
; coth x
1
tanh x
e
x
e
ÿx
e
x
ÿ e
ÿx
;
sech x
1
cosh x
2
e
x
e
ÿx
; cosech x
1
sinh x
2
e
x
ÿ e
ÿx
:
Rough graphs of these six functions are given in Fig. A1. 2.
Some fundame ntal relationships among these functions are as follows:
cosh
2
x ÿ sinh
2
x 1; sech
2
x tanh
2
x 1; coth
2
x ÿ cosech
2
x 1;
sinhx ysinh x cosh y cosh x sinh y;
coshx ycosh x cosh y sinh x sinh y;
tanhx y
tanh x tanh y
1 tanh x tanh y
:
509
FUNCTIONS
Figure A1.2. Hyperbolic functions.

Problem A1.6
Using the rules of exponents, prove that ln mnln m ln n:
Problem A1.7
Prove that: asin
2
x
1
2
1 ÿ cos 2x; cos
2
x
1
2
1 cos 2x, and (b) A cos x
B sin x
A
2
B
2
p
sinx , where tan A=B
Problem A1.8
Prove that: acosh
2
x ÿ sinh
2
x 1, and (b)
2
x tanh
2
x 1.
Limits
We are sometimes required to ®nd the limit of a function f x as x approaches
some particular value :
lim
x!
f xl:
This means that if jx ÿ j is small enough, jf xÿlj can be made as small as we
please. A more precise analytic description of lim
x!
f xl is the following:
For any ">0 (however small) we can always ®nd a number
(which, in general, depends upon ") such that f xÿl
jj
<"
whenever x ÿ
jj
<.
As an example, consider the limit of the simple function f x2 ÿ 1=x ÿ 1 as
x ! 2. Then
lim
x!2
f x1
for if we are given a number, say " 10
ÿ3
, we can always ®nd a number which is
such that
2 ÿ
1
x ÿ 1
ÿ 1 < 10
ÿ3
A1:1
provided jx ÿ 2j <. In this case (A1.1) will be true if 1=x ÿ 1 > 1 ÿ 10
ÿ3
0:999. This requires x ÿ 1 < 0:999
ÿ1
,orx ÿ 2 < 0:999
ÿ1
ÿ 1. Thus we need
only take 0:999
ÿ1
ÿ 1.
The functio n f x is said to be continuous at if lim
x!
f xl.Iff x is con-
tinuous at each point of an interval such as a x b or a < x b, etc., it is said to be
continuous in the interval (for example, a polynomial is continuous at all x).
The de®nition implies that lim
x!ÿ0
f xlim
x!0
f xf at all points
of the interval (a; b), but this is clearly inapplicable at the endpoints a and b.At
these points we de®ne continuity by
lim
x!a0
f xf a and lim
x!bÿ0
f xf b:
510
APPENDIX 1 PRELIMINARIES

A ®nite discontinuity may occur at x . This will arise when
lim
x!ÿ0
f xl
1
, lim
x!ÿ0
f xl
2
, and l
1
6 l
2
.
It is obvious that a continuous function will be bounded in any ®nite interval.
This means that we can ®nd numbers m and M independent of x and such that
m f xM for a x b. Furthermo re, we expect to ®nd x
0
; x
1
such that
f x
0
m and f x
1
M.
The order of magnitude of a function is indicated in terms of its variable. Thus,
if x is very small, and if f xa
1
x a
2
x
2
a
3
x
3
(a
k
constant), its magni-
tude is governed by the term in x and we write f x Ox. When a
1
0, we
write f xOx
2
, etc. When f xOx
n
, then lim
x!0
ff x=x
n
g is ®nite and/
or lim
x!0
ff x=x
nÿ1
g0.
A function f x is said to be diÿerentiable or to possess a derivative at the point
x if lim
h!0
f x hÿf x=h exists. We write this limit in various forms
df =dx; f
0
or Df , where D d=dx. Most of the functions in physics can be
successively diÿerentiated a number of times. These successive derivatives are
written as f
0
x; f
00
x; ...; f
n
x; ...; or Df ; D
2
f ; ...; D
n
f ; ...:
Problem A1.9
If f xx
2
, prove that: (a) lim
x!2
f x4, and b f x is continuous at x 2.
In®nite series
In®nite series involve the notion of sequence in a simple way. For example,
2
p
is
irrational and can only be expressed as a non-recurring decimal 1:414 ...: We can
approximate to its value by a sequence of rationals, 1, 1.4, 1.41, 1.414, ...say fa
n
g
which is a countable set limit of a
n
whose values approach inde®nitely close to
2
p
.
Because of this we say the limit of a
n
as n tends to in®nity exists and equals
2
p
,
and write lim
n!1
a
n
2
p
.
In general, a sequence u
1
; u
2
; ...; fu
n
g is a function de®ned on the set of natural
numbers. The sequence is said to have the limit l or to converge to l, if given any
">0 there exists a number N > 0 such that ju
n
ÿ lj <"for all n > N, and in such
case we write lim
n!1
u
n
l.
Consider now the sums of the sequence fu
n
g
s
n
X
n
r1
u
r
u
1
u
2
u
3
; A:2
where u
r
> 0 for all r.Ifn !1, then (A.2) is an in®nite series of positive terms.
We see that the behavior of this series is determined by the behavior of the
sequence fu
n
g as it converges or diverges. If lim
n!1
s
n
s (®nite) we say that
(A.2) is convergent and has the sum s. When s
n
!1as n !1, we say that (A.2)
is divergent.
511
INFINITE SERIES

Example A1.1.
Show that the series
X
1
n1
1
2
n
1
2
1
2
2
1
2
3
is convergent and has sum s 1.
Solution: Let
s
n
1
2
1
2
2
1
2
3
1
2
n
;
then
1
2
s
n
1
2
2
1
2
3
1
2
n1
:
Subtraction gives
1 ÿ
1
2
s
n
1
2
ÿ
1
2
n1
1
2
1 ÿ
1
2
n
; or s
n
1 ÿ
1
2
n
:
Then since lim
n!1
s
n
lim
n!1
1 ÿ 1=2
n
1, the series is convergent and has
the sum s 1.
Example A1.2.
Show that the series
P
1
n1
ÿ1
nÿ1
1 ÿ 1 1 ÿ 1 is diverg ent.
Solution: Here s
n
0 or 1 according as n is even or odd. Hence lim
n!1
s
n
does
not exist and so the series is divergent.
Example A1.3.
Show that the geometric series
P
1
n1
ar
nÿ1
a ar ar
2
; where a and r are
constants, ( a) converges to s a=1 ÿ r if jrj < 1; and (b) diverges if jrj > 1.
Solution: Let
s
n
a ar ar
2
ar
nÿ1
:
Then
rs
n
ar ar
2
ar
nÿ1
ar
n
:
Subtraction gives
1 ÿ rs
n
a ÿ ar
n
or s
n
a1 ÿ r
n
1 ÿ r
:
512
APPENDIX 1 PRELIMINARIES

(a)Ifjrj < 1;
lim
n!1
s
n
lim
n!1
a1 ÿ r
n
1 ÿ r
a
1 ÿ r
:
(b)Ifjrj > 1,
lim
n!1
s
n
lim
n!1
a1 ÿ r
n
1 ÿ r
does not exist.
Example A1.4.
Show that the p series
P
1
n1
1=n
p
converges if p > 1 and diverges if p 1.
Solution: Using f n1=n
p
we have f x1=x
p
so that if p 6 1,
Z
1
1
dx
x
p
lim
M!1
Z
M
1
x
ÿp
dx lim
M!1
x
1ÿp
1 ÿ p
þ
þ
þ
þ
M
1
lim
M!1
M
1ÿp
1 ÿ p
ÿ
1
1 ÿ p
"#
:
Now if p > 1 this limit exists and the corresponding series converges. But if p < 1
the limit does not exist an d the series diverges.
If p 1 then
Z
1
1
dx
x
lim
M!1
Z
M
1
dx
x
lim
M!1
ln x
þ
þ
þ
þ
M
1
lim
M!1
ln M;
which does not exist and so the corres ponding series for p 1 diverges.
This shows that 1
1
2
1
3
diverges even though the nth term approaches
zero.
Tests for convergence
There are several important tests for convergence of series of positive terms.
Before using these simple tests, we can often weed out some very badly divergent
series with the following preliminary test:
If the terms of an in®nite series do not tend to zero (that is, if
lim
n!1
a
n
6 0, the series diverges. If lim
n!1
a
n
0, we must
test further:
Four of the common tests are given below:
Comparison test
If u
n
v
n
(all n), then
P
1
n1
u
n
converges when
P
1
n1
v
n
converges. If u
n
v
n
(all
n), then
P
1
n1
u
n
diverges when
P
1
n1
v
n
diverges.
513
INFINITE SERIES

Since the behavior of
P
1
n1
u
n
is unaÿected by removing a ®nite number of
terms from the series, this test is true if u
n
v
n
or u
n
v
n
for all n > N. Note that
n > N means from some term onward. Often, N 1.
Example A1.5
(a) Since 1=2
n
11=2
n
and
P
1=2
n
converges,
P
1=2
n
1 also converges.
(b) Since 1=ln n > 1=n and
P
1
n2
1=n diverges,
P
1
n2
1=ln n also diverges.
Quotient test
If u
n1
=u
n
v
n1
=v
n
(all n ), then
P
1
n1
u
n
converges when
P
1
n1
v
n
converges. And
if u
n1
=u
n
v
n1
=v
n
(all n), then
P
1
n1
u
n
diverges when
P
1
n1
v
n
diverges.
We can write
u
n
u
n
u
nÿ1
u
nÿ1
u
nÿ2
u
2
u
1
u
1
v
n
v
nÿ1
v
nÿ1
v
nÿ2
v
2
v
1
v
1
so that u
n
v
n
u
1
which proves the quotient test by using the comparison test.
A similar argument shows that if u
n1
=u
n
v
n1
=v
n
(all n), then
P
1
n1
u
n
diverges when
P
1
n1
v
n
diverges.
Example A1.6
Consider the series
X
1
n1
4n
2
ÿ n 3
n
3
2n
:
For large n, 4n
2
ÿ n 3 = n
3
2n is approximately 4=n. Taking
u
n
4n
2
ÿ n 3=n
3
2n and v
n
1=n, we have lim
n!1
u
n
=v
n
1. Now
since
P
v
n
P
1=n diverges,
P
u
n
also diverges.
D'Alembert's ratio test:
P
1
n1
u
n
converges when u
n1
=u
n
< 1 (all n N) and diverges when u
n1
=u
n
> 1.
Write v
n
x
nÿ1
in the quotient test so that
P
1
n1
v
n
is the geometric series with
common ratio v
n1
=v
n
x. Then the quotient test proves that
P
1
n1
u
n
converges
when x < 1 and diverges when x > 1:
Sometimes the ratio test is stated in the following form: if lim
n!1
u
n1
=u
n
,
then
P
1
n1
u
n
converges when <1 and diverges when >1.
Example A1.7
Consider the series
1
1
2!
1
3!
1
n!
:
514
APPENDIX 1 PRELIMINARIES

Using the ratio test, we have
u
n1
u
n
1
n 1!
1
n!
n!
n 1!
1
n 1
< 1;
so the series converges.
Integral test.
If f x is positive, continuous and monotonic decreasing and is such that
f nu
n
for n > N, then
P
u
n
converges or diverges according as
Z
1
N
f xdx lim
M!1
Z
M
N
f xdx
converges or diverges. We often have N 1 in practice.
To prove this test, we will use the following property of de®nite integrals:
If in a x b; f xgx, then
Z
b
a
f xdx
Z
b
a
gxdx.
Now from the monotonicity of f x, we have
u
n1
f n 1f xf nu
n
; n 1; 2; 3; ...:
Integrating from x n to x n 1 and using the above quoted property of
de®nite integrals we obtain
u
n1
Z
n1
n
f xdx u
n
; n 1; 2; 3; ...:
Summing from n 1toM ÿ 1,
u
1
u
2
u
M
Z
M
1
f xdx u
1
u
2
u
Mÿ1
: A1:3
If f x is strictly decreasing, the equality sign in (A1.3) can be omitted.
If lim
M!1
R
M
1
f xdx exists and is equal to s, we see from the left hand inequal-
ity in (A1.3) that u
1
u
2
u
M
is monotonically increasing and bounded
above by s, so that
P
u
n
converges. If lim
M!1
R
M
1
f xdx is unbounded, we see
from the right hand inequality in (A1.3) that
P
u
n
diverges.
Geometrically, u
1
u
2
u
M
is the total area of the rectangles shown
shaded in Fig. A1.3, while u
1
u
2
u
Mÿ1
is the total area of the rectangles
which are shaded and non-shaded. The area under the curve y f x from x 1
to x M is intermediate in value between the two areas given above, thus illus-
trating the result (A1.3).
515
INFINITE SERIES
