Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


The Poisson distribution has the mean
EX
X
1
m0
m
m
e
ÿ
m!
X
1
m1
m
e
ÿ
m ÿ 1!
X
1
m0
m
e
ÿ
m!
e
ÿ
X
1
m0
m
m!
e
ÿ
e
; 14 :27
where we have made use of the result
X
1
m0
m
m!
e
:
The variance
2
of the Poisson distribution is
2
VarXEX ÿ EX
2
EX
2
ÿEX
2
X
1
m0
m
2
m
e
ÿ
m!
ÿ
2
e
ÿ
X
1
m1
m
m
m ÿ 1!
ÿ
2
e
ÿ
d
d
e
ÿ
ÿ
2
: 14:28
To illustrate the use of the Poisson distribution, let us consider a simple exam-
ple. Suppose the probability that an individual suÿers a bad reaction from a ¯u
injection is 0.001; what is the probability that out of 2000 individuals (a) exactly 3,
(b) more than 2 individuals will suÿer a bad reaction? Now X denotes the number
of individuals who suÿer a bad reaction and it is binomially distributed. However,
we can use the Poisson approximation, because the bad reactions are assumed to
be rare events. Thus
PX m
m
e
ÿ
m!
; with mp 2000 0:0012:
(a) PX 3
2
3
e
ÿ2
3!
0:18;
b PX > 21 ÿPX 0PX 1PX 2
1 ÿ
2
0
e
ÿ2
0!
2
1
e
ÿ2
1!
2
2
e
ÿ2
2!
"#
1 ÿ 5e
ÿ2
0:323:
An exact evaluation of the probabil ities using the binomial distribution would
require mu ch more labor.
496
INTRODUCTION TO PROBABILITY THEORY
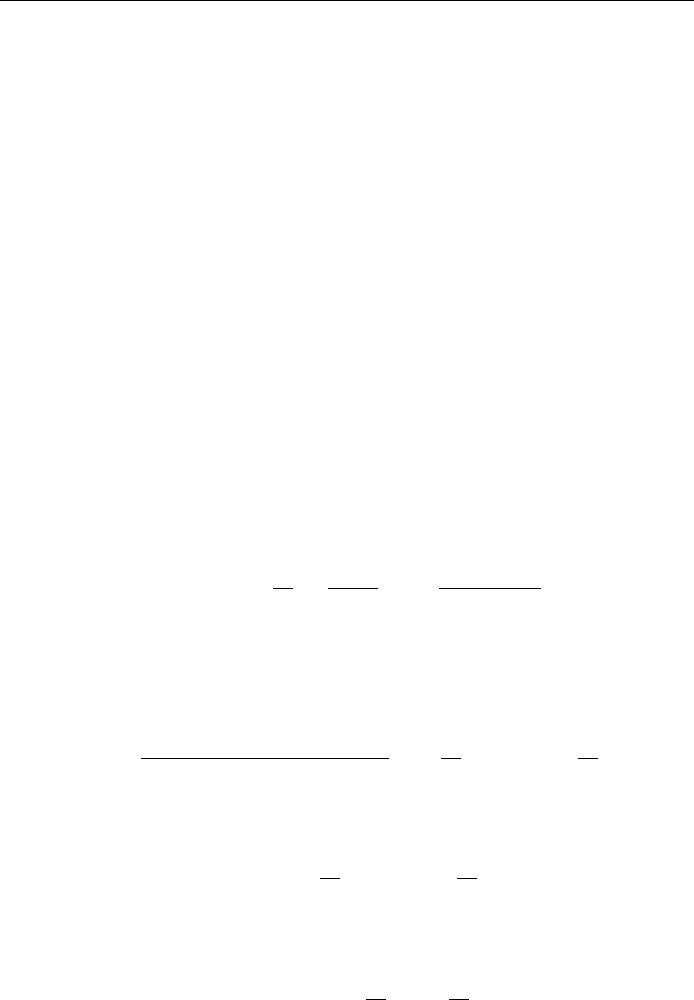
The Poisson distribution is very important in nuclear physics. Suppose that we
have n radioactive nuc lei and the probability for any one of these to decay in a
given interval of time T is p, then the probability that m nuclei will decay in the
interval T is given by the binomial distribution. However, n may be a very large
number (such as 10
23
), and p may be the order of 10
ÿ20
, and it is impractical to
evaluate the binomial distribution with numbers of these magnitudes.
Fortunately, the Poisson distribution can come to our rescue.
The Poisson distribution has its own signi®cance beyond its connection with the
binomial distribution and it can be derived mathematically from elementary con-
siderations. In general, the Poisson distribution applies when a very large number
of experiments is carried out, but the probability of success in each is very small,
so that the expected number of successes is a ®nite number.
The Gaussian (or norm al) distribution
The second limit of the binomial distribution that is of interest to us results when
both n and pn are large. Clearly, we assume that m, n,andn ÿ m are large enough
to permit the use of Stirling's formula (n!
2n
p
n
n
e
ÿn
). Replacing m!, n!, and
(n ÿ m)! by their approximations and after simpli®cation, we obtain
PX m
np
m
m
nq
n ÿ m
nÿm
n
2mn ÿ m
r
: 14:29
The binomial distribution has the mean value np (see Eq. (14.20). Now let
denote the deviation of m from np; that is, m ÿ np. Then n ÿ m nq ÿ ;
and Eq. (14.29) becomes
PX m
1
2npq 1 =np1 ÿ =np
p
1
np
ÿnp
1 ÿ
nq
ÿnq
or
PX mA 1
np
ÿnp
1 ÿ
nq
ÿnqÿ
;
where
A
2npq 1
np
1 ÿ
nq
s
:
Then
log PX mAÿnp log 1 =npÿnq ÿ log1 ÿ =nq:
497
SPECIAL PROBABILITY DISTRIBUTIONS

Assuming jj< npq, so that =npjj< 1 and =nqjj< 1, this permits us to write the
two convergent series
log 1
np
np
ÿ
2
2n
2
p
2
3
3n
3
p
3
ÿ;
log 1 ÿ
nq
ÿ
nq
ÿ
2
2n
2
q
2
ÿ
3
3n
3
q
3
ÿ:
Hence
log PX mAÿ
2
2npq
ÿ
3
p
2
ÿ q
2
2 3n
2
p
2
q
2
ÿ
4
p
3
q
3
3 4n
3
p
3
q
3
ÿ:
Now, if jj is so small in comparison with npq that we ignore all but the ®rst term
on the right hand side of this expansion and A can be replaced by 2npq
1=2
, then
we get the approximation formula
PX m
1
2npq
p
e
ÿ
2
=2npq
: 14:30
When
npq
p
; Eq. (14.30) becomes
f mPX m
1
2
p
e
ÿ
2
=2
2
: 14:31
This is called the Guassian, or normal, distribution. It is a very good approxima-
tion even for quite small values of n.
The Gaussian distribution is a symmetrical bell-shaped distribution about its
mean , and is a measure of the width of the distribution. Fig. 14.4 gives a
comparison of the binomial distribution and the Gaussian approximation.
The Gaussian distribution also has a signi®cance far beyond its connection with
the binomial distribution. It can be derived mathematically from elementary con-
siderations, and is found to agree empirically with random errors that actually
498
INTRODUCTION TO PROBABILITY THEORY
Figure 14.4.
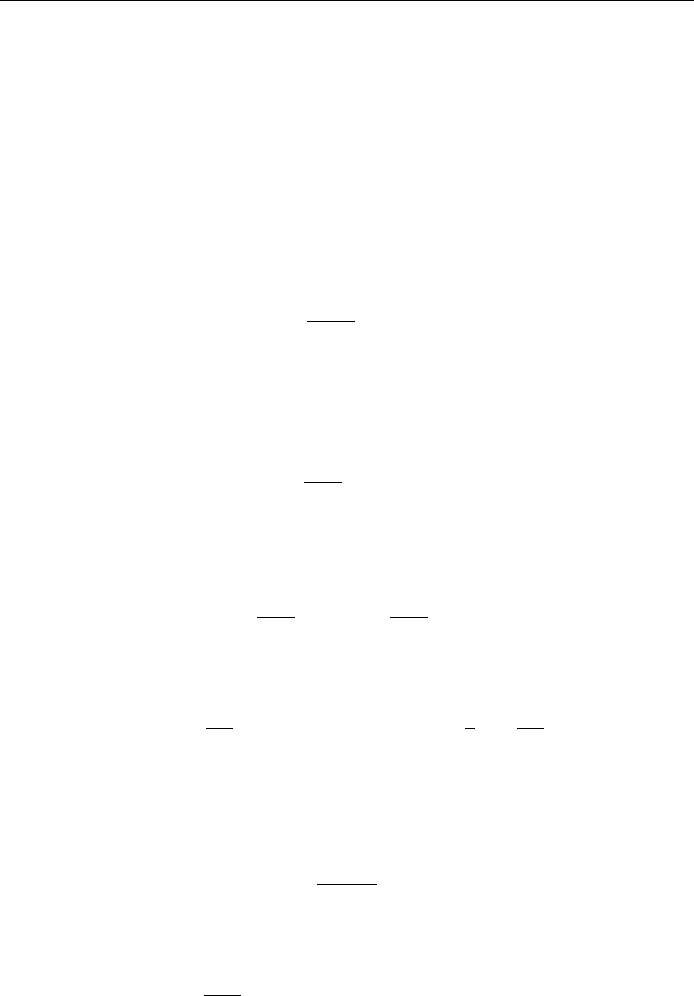
occur in experiments. Everyone believes in the Gaussian distribution: mathe-
maticians think that physicists have veri®ed it experimentally and physicists
think that mathematicians have proved it theoretically.
One of the main uses of the Gaussian distribution is to compute the probability
X
m
2
mm
1
f m
that the number of successes is between the given limits m
1
and m
2
. Eq. (14.31)
shows that the above sum may be approximated by a sum
X
1
2
p
e
ÿ
2
=2
2
14:32
over appropriate values of . Since m ÿ np, the diÿerence between successive
values of is 1, and hence if we let z =, the diÿerence between successive
values of z is z 1=. Thus Eq. (14.32) becomes the sum over z,
X
1
2
p
e
ÿz
2
=2
z: 14:33
As z ! 0, the expression (14.33) approaches an integral, which may be evalu-
ated in terms of the function
z
Z
z
0
1
2
p
e
ÿz
2
=2
dz
1
2
p
Z
z
0
e
ÿz
2
=2
dz: 14:34
The function z is related to the extensively tabulated error function, erf(z ):
erfz
2
p
Z
z
0
e
ÿz
2
dz; and z
1
2
erf
z
2
p
:
These considerations lead to the following important theorem, which we state
without proof: If m is the number of successes in n independent trials with con-
stant probability p, the probability of the inequality
z
1
m ÿ np
npq
p
z
2
14:35
approaches the limit
1
2
p
Z
z
2
z
1
e
ÿz
2
=2
dz z
2
ÿz
1
14:36
as n !1. This theorem is known as Laplace±de Moivre limit theorem.
To illustrate the use of the result (14.36), let us consider the simple example of a
die tossed 600 times, and ask what the probability is that the number of ones will
499
SPECIAL PROBABILITY DISTRIBUTIONS

be between 80 and 110. Now n 600, p 1=6, q 1 ÿ p 5=6, and m varies
from 80 to 110. Hence
z
1
80 ÿ 100
1005=6
p
ÿ2:19 and z
1
110 ÿ 100
1005=6
p
1:09:
The tabulated error function gives
z
2
1:090:362;
and
z
1
ÿ2:19ÿ2:19ÿ0:486;
where we have made use of the fact that ÿzÿz; you can check this with
Eq. (14.34). So the required probability is approximately given by
0:362 ÿÿ0 :4860:848:
Continuous distributions
So far we have discussed several discrete probability dist ributions: since measure-
ments are generally made only to a certain number of signi®cant ®gures, the
variables that arise as the result of an experiment are discrete. However, discrete
variables can be approximated by continuous ones within the experimental error.
Also, in some applications a discrete random variable is inappropri ate. We now
give a brief discussion of continuous variables that will be denoted by x. We shall
see that continuous variables are easier to handle analytically.
Suppose we want to choose a point randomly on the interval 0 x 1, how
shall we measure the probabilities associated with that event? Let us divide
this interval 0; 1 into a number of subintervals, each of length x 0:1 (Fig.
14.5), the point x is then equally likely to be in any of these subintervals. The
probability that 0:3 < x < 0:6, for example, is 0.3, as there are three favorable
cases. The probability that 0:32 < x < 0:64 is found to be 0:64 ÿ 0:32 0:32
when the interval is divided into 100 parts, and so on. From these we see that
the probability for x to be in a given subinterval of (0, 1) is the length of that
subinterval. Thus
Pa < x < bb ÿ a; 0 a b 1: 14:37
500
INTRODUCTION TO PROBABILITY THEORY
Figure 14.5.

The variable x is said to be uniformly distributed on the interval 0 x 1.
Expression (14.37) can be rewritten as
Pa < x < b
Z
b
a
dx
Z
b
a
1dx:
For a continuous variable it is customary to speak of the probability density,
which in the above case is unity. More generally, a variable may be distributed
with an arbitrary density f x. Then the expression
f zdz
measures approximately the probability that x is on the interval
z < x < z dz :
And the probability that x is on a given interval (a; b)is
Pa < x < b
Z
b
a
f xdx 14:38
as shown in Fig. 14.6.
The function f x is called the probability density function and has the proper-
ties:
(1) f x0; ÿ1 < x < 1;
(2)
Z
1
ÿ1
f xdx 1; a real-valued random variable must lie between 1.
The function
FxPX x
Z
x
ÿ1
f udu 14:39
de®nes the probability that the continuous rand om variable X is in the inter val
(ÿ1; x, and is called the cumulative distributive function. If f x is continuous,
then Eq. (14.39) gives
F
0
xf x
and we may speak of a probability diÿerential dFxf xdx:
501
CONTINUOUS DISTRIBUTIONS
Figure 14.6.

By analogy with those for discrete random variables the expected value or mean
and the variance of a continuous random variable X with probability
density function f x are de®ned, respectively, to be:
EX
Z
1
ÿ1
xf xdx; 14:40
VarX
2
EX ÿ
2
Z
1
ÿ1
x ÿ
2
f xdx: 14:41
The Gaussian (or normal) distribution
One of the most important examples of a continuous probability distribution is
the Gaussian (or normal) distribution. The density function for this distribution is
given by
f x
1
2
p
e
ÿxÿ
2
=2
2
; ÿ1< x < 1; 14:42
where and are the mean and standard deviation, respectively. The correspond-
ing distribution function is
FxP X x
1
2
p
Z
x
ÿ1
e
ÿuÿ
2
=2
2
du: 14:43
The standard normal distribution has mean zero 0 and standard devia-
tion ( 1)
f z
1
2
p
e
ÿz
2
=2
: 14:44
Any normal distribution can be `standardized' by considering the substitution
z x ÿ = in Eqs. (14.42) and (14.43). A graph of the density functi on (14.44),
known as the standard normal curve, is shown in Fig. 14.7. We have also indi-
cated the areas within 1, 2 and 3 standard deviations of the mean (that is between
z ÿ1 and 1, ÿ2 and 2, ÿ3and3):
Pÿ1 Z 1
1
2
p
Z
1
ÿ1
e
ÿz
2
=2
dz 0:6827;
Pÿ2 Z 2
1
2
p
Z
2
ÿ2
e
ÿz
2
=2
dz 0:9545;
Pÿ3 Z 3
1
2
p
Z
3
ÿ3
e
ÿz
2
=2
dz 0:9973:
502
INTRODUCTION TO PROBABILITY THEORY
The above three de®nite integrals can be evaluated by making numerical approx-
imations. A short table of the values of the integral
Fx
1
2
p
Z
x
0
e
ÿt
2
dt
1
2
1
2
p
Z
x
ÿx
e
ÿt
2
dt
is included in Appendix 3. A more complete table can be found in Tables of
Normal Probability Functions, National Bureau of Standards, Washington, DC,
1953.
The Maxwell±Boltzmann distribution
Another continuous distribution that is very important in physics is the Maxwell±
Boltzmann distribution
f x4a
a
r
x
2
e
ÿax
2
; 0 x < 1; a > 0; 14:45
where a m=2kT, m is the mass, T is the temperature (K), k is the Bol tzmann
constant, and x is the speed of a gas molecule.
Problems
14.1 If a pair of dice is rolled what is the probability that a total of 8 shows?
14.2 Four coins are tossed, and we are interested in the number of heads. What
is the probability that there is an odd number of heads? What is the prob-
ability that the third coin will land heads?
503
PROBLEMS
Figure 14.7.
14.3 Two coins are tossed. A reliable witness tells us `at least 1 coin showed
heads.' What eÿect does this have on the uniform sample space?
14.4 The tossing of two coins can be described by the following sampl e space:
Event no heads one head two head
Probability 1/4 1/2 1/4
What happens to this sample space if we know at least one coin showed
heads but have no other speci®c information?
14.5 Two dice are rolled. What are the elements of the sample space? What is the
probability that a total of 8 shows? What is the probability that at least one
5 shows?
14.6 A vessel contains 30 black balls and 20 white balls. Find the probability of
drawing a white ball and a black ball in succession from the vessel.
14.7 Find the number of diÿerent arrangements or permutations consisting of
three letters each which can be formed from the seven letters A, B, C, D, E,
F, G.
14.8 It is required to sit ®ve boys and four girls in a row so that the girls occupy
the even seats. How many such arrangements are possible?
14.9 A balanced coin is tossed ®ve times. What is the probability of obtaining
three heads and two tails?
14.10 How many diÿerent ®ve-card hands can be dealt from a shued deck of 52
cards? What is the probability that a hand de alt at random consists of ®ve
spades?
14.11 (a) Find the constant term in the expansion of (x
2
1=x
12
:
(b) Evaluate 50!.
14.12 A box contains six apples of which two a re spoiled. Apples are selected at
random without replacement until a spoiled one is found. Find the
probability distribution of the number of apples drawn from the box,
and present this distribution graphically.
14.13 A fair coin is tossed six times. What is the probability of getting exactly two
heads?
14.14 Suppose three dice are rolled simultaneou sly. What is the probability that
two 5s appear with the third face showing a diÿerent number?
14.15 Verify that
P
1
m0
PX m1 for the Poisson distribution.
14.16 Certain processors are known to have a failure rate of 1.2%. There are
shipped in batches of 150. What is the probability that a batch has exactly
one defective processor? What is the probability that it has two?
14.17 A Geiger counter is used to count the arrival of radioactive particles. Find:
(a) the probability that in time t no particles will be counted;
(b) the probability of exactly one count in time t.
504
INTRODUCTION TO PROBABILITY THEORY

14.18 Given the densit y function f x
f x
kx
2
0 < x < 3
0 otherwise
:
(
(a) ®nd the constant k;
(b) compute P1 < x < 2;
(c) ®nd the distribution function and use it to ®nd P1 < x 2:
505
PROBLEMS
