Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


The numbers (14.5) are often called binomial coecients because they arise in
the binomial expansion
x y
n
x
n
n
1
x
nÿ1
y
n
2
x
nÿ2
y
2
n
n
y
n
:
When n is very large a direct evaluation of n! is impractical. In such cases we use
Stirling's approximate formula
n!
2n
p
n
n
e
ÿn
:
The ratio of the left hand side to the right hand side approaches 1 as n !1. For
this reason the right hand side is often called an asymptotic expansion of the left
hand side.
Fundamental probability theorems
So far we have calculated probabilities by directly making use of the de®nitions; it
is doable but it is not always easy. Some important properties of probabilities will
help us to cut short our computation works. These important properties are often
described in the form of theorems. To present these important theorems, let us
consider an experiment, involving two events A and B, with N equally likely
outcomes and let
n
1
number of outcomes in which A occurs; but not B;
n
2
number of outcomes in which B occurs; but not A;
n
3
number of outcomes in which both A and B occur;
n
4
number of outcomes in which neither A nor B occurs:
This covers all pos sibilities, hence n
1
n
2
n
3
n
4
N:
The probabilities of A and B occurring are respectively given by
PA
n
1
n
3
N
; PB
n
2
n
3
N
; 14:6
the probability of either A or B (or both) occurring is
PA B
n
1
n
2
n
3
N
; 14:7
and the probability of both A and B occurring successively is
PAB
n
3
N
: 14:8
Let us rewrite PAB as
PAB
n
3
N
n
1
n
3
N
n
3
n
1
n
3
:
486
INTRODUCTION TO PROBABILITY THEORY

Now n
1
n
3
=N is PA by de®nition. After A has occurred, the only possible
cases are the n
1
n
3
cases favorable to A. Of these, there are n
3
cases favorable
to B, the quotient n
3
=n
1
n
3
represents the probability of B when it is known
that A occurred, PAB. Thus we have
PABPAP
A
B: 14:9
This is often known as the theorem of joint (or compound) probability. In words,
the joint probability (or the compound probability) of A and B is the product of
the probability that A will occur times the probability that B will occur if A does.
P
A
B is called the conditional probability of B given A (that is, given that A has
occurred).
To illustrate the theorem of joint probability (14.9), we consider the probability
of drawing two kings in succession from a shued deck of 52 playing cards. The
probability of drawing a king on the ®rst draw is 4/52. After the ®rst king has
been drawn, the probability of drawing another king from the remaining 51 cards
is 3/51, so that the probability of tw o kings is
4
52
3
51
1
221
:
If the events A and B are independent, that is, the information that A has
occurred does not in¯uence the probability of B, then P
A
BPB and the
joint probability takes the form
PABPAPB; for independent events: 14:10
As a simple example, let us toss a coin and a die, and let A be the event `head
shows' and B is the event `4 shows.' These events are independent, and hence the
probability that 4 and a head both show is
PABPAPB1=21=61=12:
Theorem (14.10) can be easily extended to any number of independent events
A; B; C; ...:
Besides the theorem of joint probability, there is a second fundamental relation-
ship, known as the theorem of total probability. To present this theorem, let us go
back to Eq. (14.4) and rewrite it in a slightly diÿerent form
PA B
n
1
n
2
n
3
N
n
1
n
2
2n
3
ÿ n
3
N
n
1
n
3
n
2
n
3
ÿn
3
N
n
1
n
3
N
n
2
n
3
N
ÿ
n
3
N
PAPBÿPAB;
PA BPAPBÿPAB : 14:11
487
FUNDAMENTAL PROBABILITY THEOREMS

This theorem can be represented diagrammatically by the intersecting points sets
A and B shown in Fig. 14.1. To illustrate this theorem, consider the simple
example of tossing two dice and ®nd the probability that at least one die gives
2. The probability that both give 2 is 1/36. The probability that the ®rst die gives 2
is 1/6, and similarly for the second die. So the probability that at least one gives 2
is
PA B1=6 1=6 ÿ 1=36 11=36:
For mutually exclusive events, that is, for events A, B which cannot both occur,
PAB0 and the theorem of total probability becomes
PA BPAPB ; for mutually exclusive events: 4:12
For example, in the toss of a die, `4 shows' (event A) and `5 shows' (event B)are
mutually exclusive, the probability of getting either 4 or 5 is
PA BPAPB1=6 1=6 1=3:
The theorems of total and joint probability for uniform sample spaces estab-
lished above are also valid for arbitrary sample spaces. Let us consider a ®nite
sample space, its events E
i
are so numbered that E
1
; E
2
; ...; E
j
are favorable to
A; E
j1
; ...; E
k
are favorable to both A and B, and E
k1
; ...; E
m
are favorable to B
only. If the associated probabilities are p
i
, then Eq. (14.11) is equivalent to the
identity
p
1
p
m
p
1
p
j
p
j1
p
k
p
j1
p
k
p
k1
p
m
ÿp
j1
p
m
:
The sums within the three parentheses on the right hand side represent, respec-
tively, PA PB; and PAB by de®nition. Similarly, we have
PABp
j1
p
k
p
1
p
k
p
j1
p
1
p
k
p
k
p
1
p
k
PAP
A
B;
which is Eq. (14.9).
488
INTRODUCTION TO PROBABILITY THEORY
Figure 14.1.

Random variables and probability distributions
As demonstrated above, simple probabilities can be computed from elem entary
considerations. We need more ecient ways to deal with probabilities of whol e
classes of events. For this purpose we now introduce the concepts of random
variables and a probability distribution.
Random variables
A process such as spinning a coin or tossing a die is called random since it is
impossible to predict the ®nal outcome from the initial state. The outcomes of a
random process are certain numerically valued variables that are often called
random variables. For example, suppose that three dimes are tossed at the
same time and we ask how many heads appear. The answer will be 0, 1, 2, or 3
heads, and the sampl e space S has 8 elements:
S fTTT; HTT; THT; TTH; HHT; HTH; THH; HHHg:
The random variable X in this case is the number of heads obtained and it
assumes the values
0; 1; 1; 1; 2; 2; 2; 3:
For instance, X 1 corresponds to each of the three outcomes:
HTT; THT; TTH. That is, the random variable X can be thought of as a function
of the number of heads appear.
A random variable that takes on a ®nite or countabl e in® nite number of values
(that is it has as many values as the natural numbers 1; 2; 3; ...) is called a discrete
random variable while one that takes on a non-countable in®nite number of
values is called a non-discrete or continuous random variable.
Probability distributions
A random variable, as illustrated by the simple example of tossing three dimes at
the same time, is a numerical-valued function de®ned on a sample space. In
symbols,
Xs
i
x
i
i 1; 2; ...; n ; 14:13
where s
i
are the elements of the sample space and x
i
are the values of the random
variable X. The set of numbers x
i
can be ®nite or in®nite.
In terms of a random variable we will write PX x
i
as the probability that
the random variable X takes the value x
i
, and PX < x
i
as the probability that
the random variable takes values less than x
i
, and so on. For simplicity, we often
write PX x
i
as p
i
. The pairs x
i
; p
i
for i 1; 2; 3; ... de®ne the probability
489
RANDOM VARIABLES AND PROBABILITY DISTRIBUTIONS

distribution or probability function for the random variable X. Evidently any
probability distribution p
i
for a discrete random variable must satisfy the follow-
ing conditions:
(i)0 p
i
1;
(ii) the sum of all the probabilities must be unity (certainty),
P
i
p
i
1:
Expectation and variance
The expectation or expected value or mean of a random variable is de®ned in
terms of a weighted average of outcomes, where the wei ghting is equal to the
probability p
i
with which x
i
occurs. That is, if X is a random variable that can take
the values x
1
; x
2
; ...; with probabilities p
1
; p
2
; ...; then the expectation or
expected value EX is de®ned by
EXp
1
x
1
p
2
x
2
X
i
p
i
x
i
: 14:14
Some authors prefer to use the symbol for the expectation value EX. For the
three dimes tossed at the same time, we have
x
i
01 2 3
p
i
1=83=83=81=8
and
EX
1
8
0
3
8
1
3
8
2
1
8
3
3
2
:
We often want to know how much the individual outcomes are scattered away
from the mean. A quantity measure of the spread is the diÿerence X ÿ EX and
this is called the deviation or residual. But the expecta tion value of the deviations
is always zero:
EX ÿ EX
X
i
x
i
ÿ EXp
i
X
i
x
i
p
i
ÿ EX
X
i
p
i
E XÿEX1 0:
This should not be particularly surprising; some of the deviations are positive, and
some are negative, and so the mean of the deviations is zero. This means that the
mean of the deviations is not very useful as a measure of spread. We get around
the problem of handling the negative deviations by squaring each deviation,
thereby obtaining a quantity that is always positive. Its expectation value is called
the variance of the set of observations and is denoted by
2
2
EX ÿ EX
2
EX ÿ
2
: 14:15
490
INTRODUCTION TO PROBABILITY THEORY

The square root of the variance, , is known as the standard deviation, and it is
always positive.
We now state some basic rules for expected values. The proofs can be found in
any standard textbook on probability and statistics. In the following c is a con-
stant, X and Y are random variables, and hX is a function of X:
(1) EcXcEX;
(2) EX YEXEY;
(3) EXYEXEY (provided X and Y are independent);
(4) EhX
P
i
hx
i
p
i
(for a ®nite distribution).
Special probability distributions
We now consider some special probability distributions in which we will use all
the things we have learned so far about probability.
The binomial distribution
Before we discuss the binomial distribution, let us introduce a term, the Bernoulli
trials. Consider an experiment such as spinning a coin or throw a die repeatedly.
Each spin or toss is called a trial. In any single trial there will be a probability p
associated with a particular event (or outcome). If p is constant throughout (that
is, does not change from one trial to the next), such trials are then said to be
independent and are known as Bernoulli trials.
Now suppose that we have n independent events of some kind (such as tossing a
coin or die), each of which has a probability p of success and probability of
q 1 ÿ p of failure. What is the probability that exactly m of the events will
succeed? If we select m events from n, the probability that these m will succeed and
all the rest n ÿ m will fail is p
m
q
nÿm
. We have considered only one particular
group or combination of m events. How many combinations of m events can be
chosen from n? It is the number of combinations of n things taken m at a time:
n
C
m
. Thus the probability that exactly m events will succeed from a group of n is
f mPX m
n
C
m
p
m
q
nÿm
n!
m!n ÿ m!
p
m
q
nÿm
: 14:16
This discrete probability function (14.16) is called the binomial distribution for X,
the random variable of the number of successes in the n trials. It gives the prob-
ability of exactly m successes in n independent trials with constant probability p.
Since many statistical studies involve repeated trials, the binomial distribution has
great practical importance.
491
SPECIAL PROBABILITY DISTRIBUTIONS
Why is the discrete probability function (14.16) called the binomial distribu-
tion? Since for m 0; 1; 2; ...; n it corresponds to successive terms in the binomial
expansion
q p
n
q
n
n
C
1
q
nÿ1
p
n
C
2
q
nÿ2
p
2
p
n
X
n
m0
n
C
m
p
m
q
nÿm
:
To illustrate the use of the binomial distribution (14.16), let us ®nd the prob-
ability that a one will appear exactly 4 times if a die is thrown 10 times. Here
n 10, m 4, p 1=6, and q 1 ÿ p5=6. Hence the probability is
f 4PX 4
10!
4!6!
1
6
4
5
6
6
0:0543:
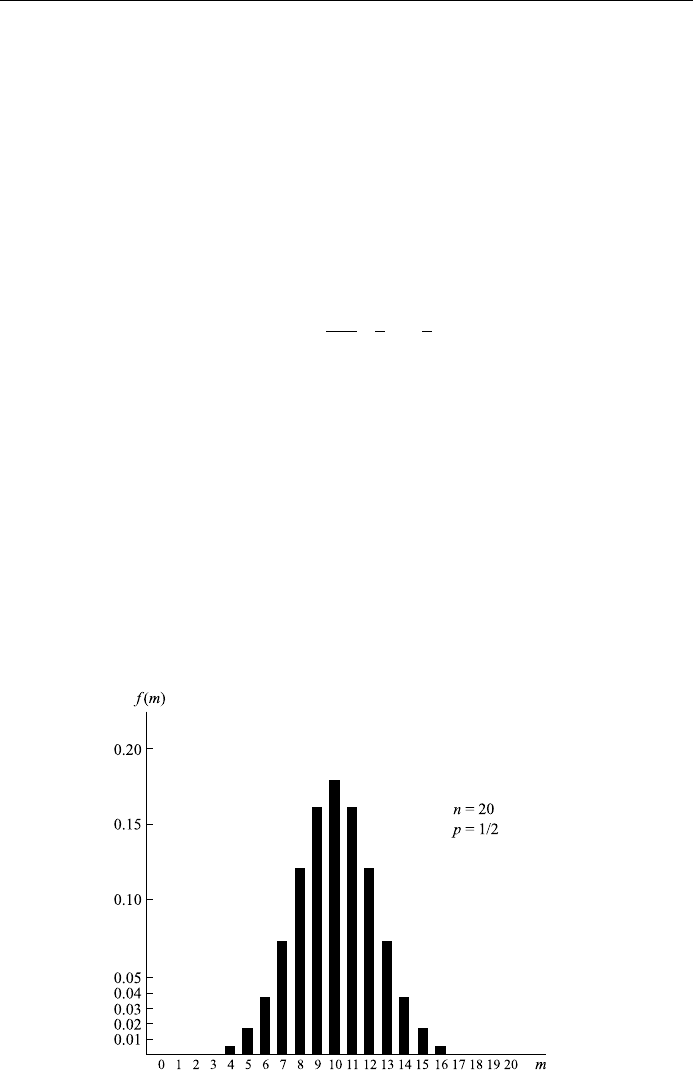
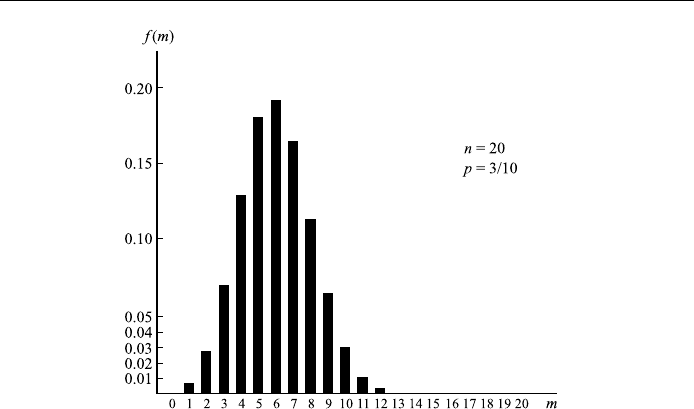
A few examples of binomial distributions, computed from Eq. (14.16), are
shown in Figs. 14.2, and 14.3 by means of histograms.
One of the key requirements for a probability distribution is that
X
n
mo
f m
X
n
mo
n
C
m
p
m
q
nÿm
1: 14:17
To show that this is in fact the case, we note that
X
n
mo
n
C
m
p
m
q
nÿm
492
INTRODUCTION TO PROBABILITY THEORY
Figure 14.2. The distribution is symmetric about m 10:
is exactly equal to the binomial expansion of q p
n
. But here q p 1, so
q p
n
1 and our proof is established.
The mean (or average) number of successes,
m, is given by
m
X
n
m0
m
n
C
m
p
m
1 ÿ p
nÿm
: 14:18
The sum ranges from m 0ton because in every one of the sets of trials the same
number of successes between 0 and n must occur. It is similar to Eq. (14.17); the
diÿerence is that the sum in Eq. (14.18) contains an extra facto r n. But we can
convert it into the form of the sum in Eq. (14.17). Diÿerentiating both sides of Eq.
(14.17) with respect to p, which is legitimate as the equation is true for all p
between 0 and 1, gives
X
n
C
m
mp
mÿ1
1 ÿ p
nÿm
ÿn ÿ mp
m
1 ÿ p
nÿmÿ1
0;
where we have dropped the limits on the sum, remem bering that m ranges from 0
to n. The last equation can be rewritten as
X
m
n
C
m
p
mÿ1
1 ÿ p
nÿm
X
n ÿ m
n
C
m
p
m
1 ÿ p
nÿmÿ1
n
X
n
C
m
p
m
1 ÿ p
nÿmÿ1
ÿ
X
m
n
C
m
p
m
1 ÿ p
nÿmÿ1
or
X
m
n
C
m
p
mÿ1
1 ÿ p
nÿm
p
m
1 ÿ p
nÿmÿ1
n
X
n
C
m
p
m
1 ÿ p
nÿmÿ1
:
493
SPECIAL PROBABILITY DISTRIBUTIONS
Figure 14.3. The distribution favors smaller value of m.

Now multiplying both sides by p1 ÿ p we get
X
m
n
C
m
1 ÿ pp
m
1 ÿ p
nÿm
p
m1
1 ÿ p
nÿm
np
X
n
C
m
p
m
1 ÿ p
nÿm
:
Combining the two terms on the left hand side, and using Eq. (14.17) in the right
hand side we have
X
m
n
C
m
p
m
1 ÿ p
nÿm
X
mf mnp: 14:19
Note that the left hand side is just our original expression for
m, Eq. (14.18). Thus
we conclude that
m np 14:20
for the binomial distribution.
The variance
2
is given by
2
X
m ÿ
m
2
f m
X
m ÿ np
2
f m; 14 :21
here we again drop the summation limits for convenience. To evaluate this sum
we ®rst rewrite Eq. (14.21) as
2
X
m
2
ÿ 2mnp n
2
p
2
f m
X
m
2
f mÿ2np
X
mf mn
2
p
2
X
f m:
This reduces to, with the help of Eqs. (14.17) and (14.19),
2
X
m
2
f mÿnp
2
: 14:22
To evaluate the ®rst term on the right hand side, we ®rst diÿerentiate Eq. (14.19):
X
m
n
C
m
mp
mÿ1
1 ÿ p
nÿm
ÿn ÿ mp
m
1 ÿ p
nÿmÿ1
p;
then multiplying by p1 ÿ p and rearr anging terms as before
X
m
2
n
C
m
p
m
1 ÿ p
nÿm
ÿ np
X
m
n
C
m
p
m
1 ÿ p
nÿm
np1 ÿ p:
By using Eq. (14.19) we can simplify the second term on the left hand side and
obtain
X
m
2
n
C
m
p
m
1 ÿ p
nÿm
np
2
np1 ÿ p
or
X
m
2
f mnp1 ÿ p np:
Inserting this result back into Eq. (14.22), we obtain
2
np1 ÿ p npÿnp
2
np1 ÿ pnpq; 14:23
494
INTRODUCTION TO PROBABILITY THEORY

and the standard deviation ;
npq
p
: 14:24
Two diÿerent limits of the binomial distribution for large n are of practical
importance: (1) n !1and p ! 0 in such a way that the product np remains
constant; (2) both n and pn are large. The ®rst case will result a new distribution,
the Poisson distribution, and the second cases gives us the Gaussian (or Laplace)
distribution.
The Poisson distribution
Now np ; so p =n. The binomial distribution (14.16) then becomes
f mPX m
n!
m!n ÿ m!
n
m
1 ÿ
n
nÿm
nn ÿ 1n ÿ 2n ÿ m 1
m!n
m
m
1 ÿ
n
nÿm
1 ÿ
1
n
1 ÿ
2
n
1 ÿ
m ÿ 1
n
m
m!
1 ÿ
n
nÿm
: 14:25
Now as n !1,
1 ÿ
1
n
1 ÿ
2
n
1 ÿ
m ÿ 1
n
! 1;
while
1 ÿ
n
nÿm
1 ÿ
n
n
1 ÿ
n
ÿm
! e
ÿ
ÿ
1e
ÿ
;
where we have made use of the result
lim
n!1
1
n
n
e
:
It follows that Eq. (14.25) becomes
f mPX m
m
e
ÿ
m!
: 14:26
This is known as the Poisson distribution. Note that
P
1
m0
PX m1; as it
should.
495
SPECIAL PROBABILITY DISTRIBUTIONS
