Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


We can express the transformation matrix in exponential form:
1 iþ
ÿiþ 1
þ!
10
01
þ
0 i
ÿi 0
~
I þ ~;
where
~
I
10
01
; ~
0 i
ÿi 0
:
Note that ~ is the negative of the Pauli spin matrix ~
2
. Now we have
x
0
1
x
0
4
þ!
~
I þ ~
x
1
x
4
þ!
:
We can generate a ®nite transformation by repeating the in®nitesimal transforma-
tion N times with Nþ :
x
0
1
x
0
4
~
I
~
N
N
x
1
x
4
:
In the limit as N !1,
lim
N!1
~
I
~
N
N
e
~
:
Now we can expand the expon ential in a Maclaurin series:
e
~
~
I ~ ~
2
=2! ~
3
=3!
and, noting that ~
2
1 and
sinh
3
=3!
5
=5!
7
=7! ;
cosh 1
2
=2!
4
=4!
6
=6! ;
we ®nally obtain
e
~
~
I cosh ~ sinh :
Our ®nite Lorentz transformation then takes the form:
x
0
1
x
0
2
cosh i sinh
ÿi sinh cosh
x
1
x
2
;
and ~ is the generator of the representations of our Lorentz transformation. The
transformation
cosh i sinh
ÿi sinh cosh
456
ELEMENTS OF GROUP THEORY

can be interpreted as the rotation matrix in the complex x
4
x
1
plane (Problem
12.16).
It is straightforward to g eneralize the above discussion to the general case
where the relative velocity is in an arbit rary direction. The transformation matrix
will be a 4 4 matrix, instead of a 2 2 matrix one. For this general case, we have
to take x
2
- and x
3
-axes into consideration.
Problems
12.1. Show that
(a) the unit element (the identity) in a group is unique, and
(b) the inverse of each group element is unique.
12.2. Show that the set of complex numbers 1; i; ÿ1, and ÿi form a group of
order four under multiplication.
12.3. Show that the set of all rational numbers, the set of all real numbers,
and the set of all complex numbers form in®nite Abelian groups under
addition.
12.4. Show that the four matrices
~
A
10
01
;
~
B
01
ÿ10
;
~
C
ÿ10
0 ÿ1
;
~
D
0 ÿ1
10
form an Abelian group of order four under multiplication.
12.5. Show that the set of all permutations of three objects
123; 231; 312; 132; 321; 213
forms a non-Abelian group of order six, with sequential performance as
the law of combinat ion.
12.6. Given two elements A and B subject to the relations A
2
B
2
E (the
identity), show that:
(a) AB 6 BA, and
(b) the set of six elements E; A; B; A
2
; AB; BA form a group.
12.7. Show that the set of elements 1; A; A
2
; ...; A
nÿ1
, A
n
1, where A e
2i=n
forms a cyclic group of order n under multiplication.
12.8. Consider the rotations of a line about the z-axis through the angles
=2;;3=2; and 2 in the xy plane. This is a ®nite set of four elements,
the four operations of rotating through =2;;3=2, and 2. Show that
this set of elements forms a group of order four under addition.
12.9. Construct the group multiplication table for the group of Problem 12.2.
12.10. Consider the possible rearrangement of two objects. The operation E
p
leaves each object in its place, and the operation I
p
interchanges the two
objects. Show that the two operations form a group that is isomorphic to
G
2
.
457
PROBLEMS
Next, we associate with the two operations two operator s
^
O
E
p
and
^
O
I
p
,
which act on the real or complex function f x
1
; y
1
; z
1
; x
2
; y
2
; z
2
with the
following eÿects:
^
O
E
p
f f ;
^
O
I
p
f x
1
; y
1
; z
1
; x
2
; y
2
; z
2
f x
2
; y
2
; z
2
; x
1
; y
1
; z
1
:
Show that the two operators form a group that is isomorphic to G
2
.
12.11. Verify that the multiplication table of S
3
has the form:
12.12. Show that an n n orthogonal matrix has nn ÿ 1=2 independent
elements.
12.13. Show that the 2 2 matrix
2
can be obtained from the rotation matrix
R by diÿerentiation at the identity of SO2, that is, 0.
12.14. Show that an n n unitary matr ix has n
2
ÿ 1 independent parameters.
12.15. Show that det e
~
A
e
Tr
~
A
where
~
A is any square matrix.
12.16. Show that the Lorentz transformation
x
0
1
ÿx
1
iþx
4
;
x
0
2
x
2
;
x
0
3
x
3
;
x
0
4
ÿx
4
ÿ iþx
1
corresponds to an imaginary rotation in the x
4
x
1
plane. (A detailed dis-
cussion of this can be found in the book Classical Mechanics, by Tai L.
Chow, John Wiley, 1995.)
458
ELEMENTS OF GROUP THEORY
P
1
P
2
P
3
P
4
P
5
P
6
P
1
P
1
P
2
P
3
P
4
P
5
P
6
P
2
P
2
P
1
P
6
P
5
P
6
P
4
P
3
P
3
P
4
P
5
P
6
P
2
P
1
P
4
P
4
P
5
P
3
P
1
P
6
P
2
P
5
P
5
P
3
P
4
P
2
P
1
P
6
P
6
P
6
P
2
P
1
P
3
P
4
P
5

13
Numerical methods
Very few of the mathematical problems which arise in physical sciences and
engineering can be solved analytically. Therefore, a simple, perhaps crude, tech-
nique giving the desired values within speci®ed limits of tolerance is often to be
preferred. We do not give a full coverage of numerical analysis in this chapter; but
some methods for numerically carrying out the processes of interpolation, ®nding
roots of equations, integration, and solving ordinary diÿerential equations will be
presented.
Interpolation
In the eighteenth century Euler was probably the ®rst person to use the interpola-
tion technique to construct planetary elliptical orbits from a set of observed
positions of the planets. We discuss here one of the most common interpolation
techniques: the polynomial interpolation. Suppose we have a set of observed or
measured data x
0
; y
0
, x
1
; y
1
; ...; x
n
; y
n
, how do we represent them by a
smooth curve of the form y f x? For analytical convenience, this smooth
curve is usually assumed to be polynomial:
f xa
0
a
1
x
1
a
2
x
2
a
n
x
n
13:1
and we use the given points to evaluate the coecients a
0
; a
1
; ...; a
n
:
f x
0
a
0
a
1
x
0
a
2
x
2
0
a
n
x
n
0
y
0
;
f x
1
a
0
a
1
x
1
a
2
x
2
1
a
n
x
n
1
y
1
;
.
.
.
f x
n
a
0
a
1
x
n
a
2
x
2
n
a
n
x
n
n
y
n
:
9
>
>
>
>
>
=
>
>
>
>
>
;
13:2
This provides n 1 equations to solve for the n 1 coecients a
0
; a
1
; ...; a
n
:
However, straightforward evaluation of coecients in the way outlined above
459

is rather tedious, as shown in Problem 13.1, hence many shortcuts have been
devised, though we will not discuss these here because of limited space.
Finding roots of equations
A solution of an equation f x0 is sometimes called a root, where f x is a real
continuous function. If f x is suciently complicated that a direct solution may
not be possible, we can seek approximate solutions. In this section we will sketch
some simple methods for determining the approximate solutions of algebraic and
transcendental equations. A polynomial equatio n is an algebraic equation. An
equation that is not reducible to an algebraic equation is c alled trans cendental.
Thus, tan x ÿ x 0ande
x
2cosx 0 are transcendental equations.
Graphical methods
The approximate solution of the equation
f x0 13:3
can be found by graphing the function y f x and reading from the graph the
values of x for which y 0. The graphing procedure can often be simpli®ed by
®rst rewriting Eq. (13.3) in the form
gxhx13:4
and then graphing y gx and y hx. The x values of the intersection points
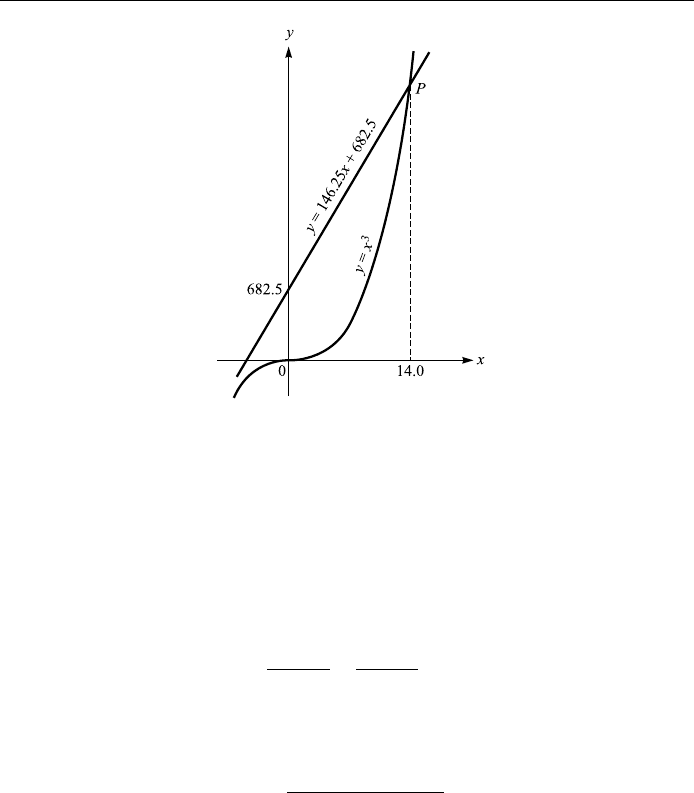
of the two curves gives the approximate values of the roots of Eq. (13.4). As an
example, consider the equation
f xx
3
ÿ 146:25x ÿ 682:5 0;
we can graph
y x
3
ÿ 146:25x ÿ 682:5
to ®nd its roots. But it is simpler to graph the two curves
y x
3
a cubic
and
y 146:25x 682:5 a straight line:
See Fig. 13.1.
There is one drawback of graphical methods: that is, they require plotting
curves on a large scale to obtain a high degree of accuracy. To avoid this, methods
of successive approximations (or simple iterative methods) have been devised, and
we shall sketch a couple of these in the following sections.
460
NUMERICAL METHODS
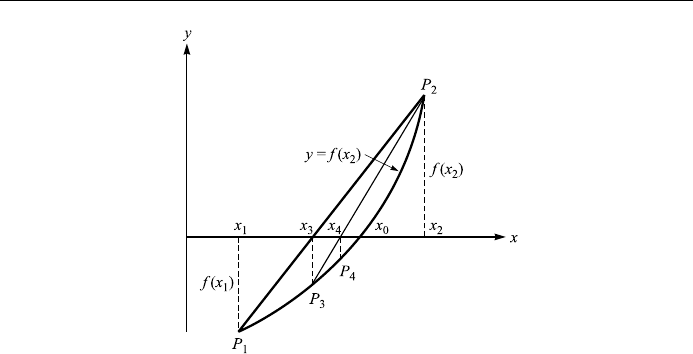
Method of linear interpolation (method of false position)
Make an initial guess of the root of Eq. (13.3), say x
0
, located between x
1
and x
2
,
and in the interval (x
1
; x
2
) the graph of y f x has the appearance as shown in
Fig. 13.2. The straight line connecting P
1
and P
2
cuts the x-axis at point x
3
; which
is usually closer to x
0
than either x
1
or x
2
. From similar triangles
x
3
ÿ x
1
ÿf x
1
x
2
ÿ x
1
f x
2
;
and solving for x
3
we get
x
3
x
1
f x
2
ÿx
2
f x
1
f x
2
ÿf x
1
:
Now the straight line connecting the points P
3
and P
2
intersects the x-axis at point
x
4
, which is a closer approximation to x
0
than x
3
. By repeating this process we
obtain a sequence of values x
3
; x
4
; ...; x
n
that generally converges to the root of
the equati on.
The iterative method described above can be simpli®ed if we rewrite Eq. (13.3)
in the form of Eq. (13.4). If the roots of
gxc 13:5
can be determined for every real c, then we can start the iterative process as
follows. Let x
1
be an approximate value of the root x
0
of Eq. (13.3) (and, of
461
METHOD OF LINEAR INTERPOLATION
Figure 13.1.
course, also equation 13.4). Now setting x x
1
on the right hand side of Eq.
(13.4) we obtain the equation
gxhx
1
; 13:6
which by hypothesis we can solve. If the solution is x
2
, we set x x
2
on the right
hand side of Eq. (13.4) and obtain
gxhx
2
: 13:7
By repeating this process, we obtain the nth approximation
gxhx
nÿ1
: 13:8
From geometric co nsiderations or interpretation of this procedure, we can see
that the sequence x
1
; x
2
; ...; x
n
converges to the root x 0 if, in the interval
2jx
1
ÿ x
0
j centered at x
0
, the following conditions are met:
1jg
0
xj > jh
0
xj; and
2 The derivatives are bounded:
)
13:9
Example 13.1
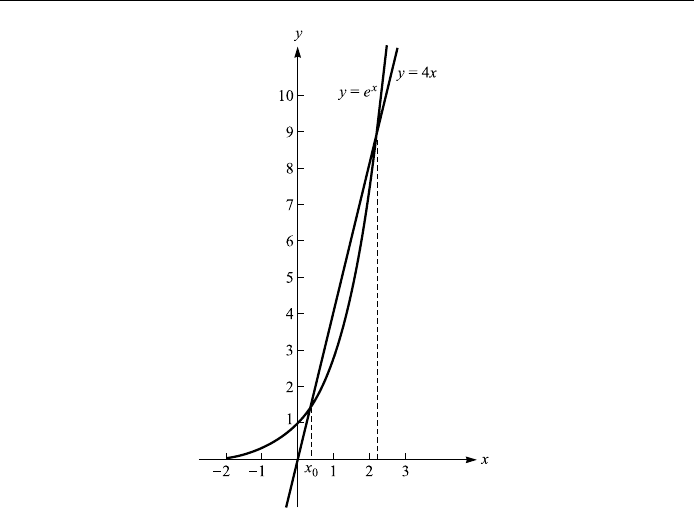
Find the approximate values of the real roots of the transcendental equation
e
x
ÿ 4x 0:
Solution: Let gxx and hxe
x
=4; so the original equation can be rewrit-
ten as
x e
x
=4:
462
NUMERICAL METHODS
Figure 13.2.
According to Eq. (13.8) we have
x
n1
e
x
n
=4; n 1; 2; 3; ...: 13:10
There are two roots (see Fig. 13.3), with one around x 0:3: If we take it as x
1
,
then we have, from Eq. (13.10)
x
2
e
x
1
=4 0:3374;
x
3
e
x
2
=4 0:3503;
x
4
e
x
3
=4 0:3540;
x
5
e
x
4
=4 0:3565;
x
6
e
x
5
=4 0:3571;
x
7
e
x
6
=4 0:3573:
The computations can be terminated at this point if only three-decimal-place
accuracy is required.
The second root lies between 2 and 3. As the slope of y 4x is less than that of
y e
x
, the ®rst condition of Eq. (13.9) cannot be met, so we rewrite the original
equation in the form
e
x
4x; or x log 4x
463
Figure 13.3.
METHOD OF LINEAR INTERPOLATION

and take gxx, hxlog 4x. We now have
x
n1
log 4x
n
; n 1; 2; ...:
If we take x
1
2:1, then
x
2
log 4x
1
2:12823;
x
3
log 4x
2
2:14158;
x
4
log 4x
3
2:14783;
x
5
log 4x
4
2:15075;
x
6
log 4x
5
2:15211;
x
7
log 4x
6
2:15303;
x
8
log 4x
7
2:15316;
and we see that the value of the root correct to three decimal places is 2.153.
Newton's method
In Newton's method, the successive terms in the sequence of approximate values
x
1
; x
2
; ...; x
n
that converges to the root is obtained by the intersection with the x-
axis of the tangent line to the curve y f x. Fig. 13.4 shows a por tion of the
graph of f x close to one of its roots, x
0
. We start with x
1
, an initial guess of the
value of the root x
0
. Now the equation of the tangent line to y f x at P
1
is
y ÿ f x
1
f
0
x
1
x ÿ x
1
: 13:11
This tangent line intersects the x-axis at x
2
that is a better approximation to the
root than x
1
. To ®nd x
2
, we set y 0 in Eq. (13.11) and ®nd
x
2
x
1
ÿ f x
1
=f
0
x
1
464
NUMERICAL METHODS
Figure 13.4.

provided f
0
x
1
60. The equation of the tangent line at P
2
is
y ÿ f x
2
f
0
x
2
x ÿ x
2
and it intersects the x-axis at x
3
:
x
3
x
2
ÿ f x
2
=f
0
x
2
:
This process is continued until we reach the desired level of accuracy. Thus , in
general
x
n1
x
n
ÿ
f x
n
f
0
x
n
; n 1; 2; ...: 13:12
Newton's method may fail if the function has a point of in¯ection, or other bad
behavior, near the root. To illustrate Newton's method, let us consider the follow-
ing trivial example.
Example 13.2
Solve, by Newton's method, x
3
ÿ 2 0.
Solution: Here we have y x
3
ÿ 2. If we take x
1
1:5 (note that 1 < 2
1=3
< 3,
then Eq. (13.12) gives
x
2
1:296296296;
x
3
1:260932225;
x
4
1:259921861;
x
5
1:25992105
x
6
1:25992105
)
repetition:
Thus, to eight-decimal-place accuracy, 2
1=3
1:25992105.
When applying Newton's method, it is often convenient to replace f
0
x
n
by
f x
n
ÿf x
n
;
with small. Usually 0:001 will give good accuracy. Eq. (13.12) then reads
x
n1
x
n
ÿ
f x
n
f x
n
ÿf x
n
; n 1; 2; ...: 13 :13
Example 13.3
Solve the equation x
2
ÿ 2 0.
465
METHOD OF LINEAR INTERPOLATION
