Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


Then using the relat ion
Z
t
a
Z
t
a
f ydydt
Z
t
a
t ÿ yf ydy;
we can rewrite the last equation as
xtÿ
Z
t
a
Ayt ÿ y ByÿA
0
y
ÿ
xydy
Z
t
a
t ÿ ygydy Aax
0
x
0
0
t ÿ ax
0
; 11:38
which can be put into the form of a Volterra equation of the second kind
xtf t
Z
t
a
Kt; yxydy ; 11:39
with
Kt; yy ÿ tBy ÿA
0
y ÿ Ay; 11:39a
f t
Z
t
0
t ÿ ygydy Aax
0
x
0
0
t ÿ ax
0
: 11:39b
Use of integral equations
We have learned how linear integral equations of the more common types may be
solved. We now show some uses of integral equations in physics; that is, we are
going to state some physical problems in integral equation form. In 1823, Abel
made one of the earliest applications of integral equations to a physical problem.
Let us take a brief look at this old problem in mechanics.
Abel's integral equation
Consider a particle of mass m falling along a smooth curve in a vertical plane, the
yz plane, under the in¯uence of gravity, which acts in the negative z direction.
Conservation of energy gives
1
2
m
_
z
2
_
y
2
mgz E;
where
_
z dz=dt; and
_
y dy=dt: If the shape of the curve is given by y Fz,we
can write
_
y dF=dz
_
z. Substituting this into the energy conservation equation
and solving for
_
z, we obtain
_
z
2E=mÿ2gz
p
1 dF=dz
2
q
E=mgÿz
p
uz
; 11:40
426
SIMPLE LINEAR INTEGRAL EQUATIONS

where
uz
1 dF=dz
2
=2g
q
:
If
_
z 0andz z
0
at t 0, then E=mg z
0
and Eq. (11.40) becomes
_
z
z
0
ÿ z
p
uz:
Solving for time t, we obtain
t ÿ
Z
z
0
z
uz
z
0
ÿ z
p
dz
Z
z
z
0
uz
z
0
ÿ z
p
dz;
where z is the height the particle reaches at time t.
Classical simple harmonic oscillator
Consider a linear oscillator
x !
2
x 0; with x00;
_
x01:
We can transform this diÿerential equation into an integral equation.
Comparing with Eq. (11.37), we have
At0; Bt!
2
; and gt0:
Substituting these into Eq. (11.38) (or (11.39), (11.39a), and (11.39b)), we obtain
the integral equation
xtt !
2
Z
t
0
y ÿ txydy;
which is equivalent to the original diÿerential equation plus the initial conditions.
Quantum simple harmonic oscillator
The Schro
È
dinger equation for the energy eigenstates of the one-dimensional
simple harmonic oscillat or is
ÿ
p
2
2m
d
2
þ
dx
2
1
2
m!
2
x
2
þ Eþ: 11:41
Changing to the dimensionless variable y
m!=p
p
x, Eq. (11.41) reduces to a
simpler form:
d
2
þ
dy
2
2
ÿ y
2
þ 0; 11:42
where
2E=p !
p
. Taking the Fourier transform of Eq. (11.42), we obtain
d
2
gk
dk
2
2
ÿ k
2
gk0; 11:43
427
USEOFINTEGRALEQUATIONS

where
gk
1
2
p
Z
1
ÿ1
þye
iky
dy 11:44
and we also assume that þ and þ
0
vanish as y !1.
Eq. (11.43) is formally identical to Eq. (11.42). Since quantities such as the total
probability and the expectation value of the potential energy must be remain ®nite
for ®nite E, we should expect gk; dgk=dk ! 0ask !1. Thus g and þ diÿer
at most by a normalization constant
gkcþk:
It follows that þ satis®es the integral equation
cþk
1
2
p
Z
1
ÿ1
þye
iky
dy: 11:45
The constant c may be determined by substituting cþ on the right hand side:
c
2
þk
1
2
Z
1
ÿ1
Z
1
ÿ1
þze
izy
e
iky
dzdy
Z
1
ÿ1
þzz kdz
þÿk:
Recall that þ may be simultaneously chosen to be a parity eigenstate
þÿxþx. We see that eigenstates of even parity require c
2
1, or
c 1; and for eigenstates of odd parit y we have c
2
ÿ1, or c i.
We shall leave the solution of Eq. (11.45), which can be approached in several
ways, as an exercise for the reader.
Problems
11.1 Solve the following integral equations:
(a) ux
1
2
ÿ x
Z
1
0
utdt;
(b) ux
Z
1
0
utdt;
(c) uxx
Z
1
0
utdt:
11.2 Solve the Fredholm equation of the second kind
f xux
Z
b
a
Kx; tu tdt;
where f xcosh x; Kx; txt.
428
SIMPLE LINEAR INTEGRAL EQUATIONS

11.3 The homogeneous Fredholm equation
ux
Z
=2
0
sin x sin tutdt
only has a solution for a particular value of . Find the value of and the
solution co rresponding to this value of .
11.4 Solve homogeneous Fredh olm equation ux
R
1
ÿ1
t xutdt. Find the
values of and the corresponding solutions.
11.5 Check the convergence of the Neumann series (11.14) by the Cauchy ratio
test.
11.6 Transform the follo wing diÿerential equations into integral equations:
a
dx
dt
ÿ x 0 with x 1 when t 0;
b
d
2
x
dt
2
dx
dt
x 1 with x 0;
dx
dt
1 when t 0 :
11.7 By using the Laplace transformation and the convolution theorem solve the
equation
uxx
Z
x
0
sinx ÿ tutdt:
11.8 Given the Fredholm integral equation
e
ÿx
2
Z
1
ÿ1
e
ÿxÿt
2
utdt;
apply the Fouurier convolution technique to solve it for ut.
11.9 Find the solution of the Fredholm equation
uxx
Z
1
0
x tutdt
by the Schmidt±Hilbert method for not equal to an eigenvalue. Show that
there are no solutions when is an eigenvalue.
429
PROBLEMS

12
Elements of group theory
Group theory did not ®nd a use in physics until the advent of modern quantum
mechanics in 1925. In recent years group theory has been applied to many
branches of physics and physica l chemistry, notably to problems of molecules,
atoms an d atomic nuclei. Mostly recently, group theory has been being applied in
the search for a pattern of `family' relationships between elementary particles.
Mathematicians are generally more interested in the abstract theory of groups,
but the representation theory of groups of direct use in a large variety of physical
problems is more useful to physicists. In this chapter, we shall give an elementary
introduction to the theory of groups, which will be need ed for understanding the
representation theory.
De®nition of a group (group axioms)
A group is a set of distinct elements for which a law of `combination' is well
de®ned. Hence, before we give `group' a formal de®nition, we must ®rst de®ne
what kind of `elements' do we mean. Any collection of objects, quantities or
operators form a set, and each individual object, quantity or operator is called
an element of the set.
A group is a set of elements A, B, C; ...; ®nite or in®nite in number, with a rule
for combining any two of them to form a `product', subject to the following four
conditions:
(1) The product of any two group elements must be a group element; that is, if
A and B are members of the group, then so is the product AB.
(2) The law of composition of the group elements is associative; that is, if A, B,
and C are members of the group, then ABC ABC.
(3) There exists a unit group element E, called the identity, such that
EA AE A for every member of the group.
430

(4) Every element has a unique inverse, A
ÿ1
, such that AA
ÿ1
A
ÿ1
A E.
The use of the word `product' in the above de®nition require s comment. The
law of combination is commonly referred as `multiplication', and so the result of a
combination of elements is referred to as a `product'. However, the law of com-
bination may be ordinary addition as in the group consisting of the set of all
integers (positive, negati ve, and zero). Here AB A B, `zero' is the identity, and
A
ÿ1
ÿA. The word `product' is meant to symbolize a broad meaning of
`multiplication' in group theory, as will become clearer from the examples below.
A group with a ®nite number of elements is called a ®nite group; and the
number of elements (in a ®nite group) is the order of the group.
A grou p containing an in®nite number of elements is call ed an in®nite group.
An in®nite group may be either discrete or continuous. If the number of the
elements in an in®nite group is denumerably in®nite, the group is discrete; if
the number of elements is non-denumerably in®nite, the group is continuous.
A group is called Abelian (or commutative) if for every pair of elements A, B in
the group, AB BA. In general, groups are not Abelian and so it is necessary to
preserve carefully the order of the factors in a group `product'.
A subgroup is any subset of the elements of a group that by themselves satisfy
the group axioms with the same law of combination.
Now let us consider some examples of groups.
Example 12.1
The real numbers 1 and ÿ1 form a group of order two, under multiplication. The
identity element is 1; and the inverse is 1=x, where x stands for 1 or ÿ1.
Example 12.2
The set of all integers (positive, negative, and zero) forms a discrete in®nite group
under addition. The identity element is zero; the inverse of each element is its
negative. The group axioms are satis®ed:
(1) is satis®ed because the sum of any two integers (including any integer with
itself) is always another integer.
(2) is satis®ed because the associative law of addition A B C
A BC is true for integers.
(3) is satis®ed because the addition of 0 to any integer does not alter it.
(4) is satis®ed because the addition of the inverse of an integer to the integer
itself alwa ys gives 0, the identity element of our group: A ÿA0.
Obviously, the group is Abelian since A B B A. We denote this group by
S
1
.
431
DEFINITION OF A GROUP (GROUP AXIOMS)

The same set of all integers does not form a group under multiplication. Why?
Because the inverses of integers are not integers and so they are not members of
the set.
Example 12.3
The set of all rational numbers (p=q, with q 6 0) forms a continuous in®nite group
under addition. It is an Abelian group, and we denote it by S
2
. The identity
element is 0; and the invers e of a given elem ent is its negative.
Example 12.4
The set of all complex numbers z x iy forms an in®nite group under
addition. It is an Abelian group and we denote it by S
3
. The identity element
is 0; and the inverse of a given element is its negative (that is, ÿz is the inverse
of z).
The set of elements in S
1
is a subset of elements in S
2
, and the set of elements in
S
2
is a subset of elements in S
3
. Furthermore, each of these sets forms a group
under addition, thus S
1
is a subgroup of S
2
,andS
2
a subgroup of S
3
. Obviously
S
1
is also a subgroup of S
3
.
Example 12.5
The three matrices
~
A
10
01
;
~
B
01
ÿ1 ÿ1
;
~
C
ÿ1 ÿ1
10
form an Abelian group of order three under matrix multiplication. The identity
element is the unit matrix, E
~
A. The inverse of a given matrix is the inverse
matrix of the given matrix:
~
A
ÿ1
10
01
~
A;
~
B
ÿ1
ÿ1 ÿ1
10
~
C;
~
C
ÿ1
01
ÿ1 ÿ1
~
B:
It is straightforward to check that all the four gro up axioms are satis®ed. We
leave this to the reader.
Example 12.6
The three permutation operations on three objects a; b; c
123; 231; 312
form an Abelian group of order three with sequential performance as the law of
combination.
The operation [1 2 3] means we put the object a ®rst, object b second, and object
c third. And two elements are multiplied by performing ®rst the operation on the
432
ELEMENTS OF GROUP THEORY

right, then the ope ration on the left. For example
231312abc 231cab abc:
Thus two operations performed sequentially are equivalent to the operation
[1 2 3]:
231312123:
similarly
312231abc 312bca abc;
that is,
312231123:
This law of combination is commutative. What is the identity element of this
group? And the inverse of a given element? We leave the reader to answer these
questions. The group illustrated by this example is known as a cyclic group of
order 3, C
3
.
It can be shown that the set of all permutations of three objects
123; 231; 312; 132; 321; 213
forms a non-Abelian group of order six denoted by S
3
. It is called the symmetric
group of three objects. Note that C
3
is a subgroup of S
3
.
Cyclic groups
We now revisit the cyclic groups. The elements of a cyclic group can be expressed
as power of a single element A, say, as A; A
2
; A
3
; ...; A
pÿ1
; A
p
E; p is the smal-
lest integer for which A
p
E and is the order of the group. The inverse of A
k
is
A
pÿk
, that is, an element of the set. It is straightforward to check that all group
axioms are satis®ed. We leave this to the reader. It is obvious that cyclic groups
are Abelian since A
k
A AA
k
k < p.
Example 12.7
The complex numbers 1, i; ÿ1; ÿi form a cyclic group of order 3. In this case,
A i and p 3: i
n
, n 0; 1; 2; 3. These group elements may be interpreted as
successive 908 rotations in the complex plane 0;=2;; and 3=2. Con-
sequently, they can be represented by four 2 2 matrices. We shall come back
to this later.
Example 12.8
We now consider a second example of cyclic groups: the group of rotations of an
equilateral triangle in its plane about an axis passing through its center that brings
433
CYCLIC GROUPS
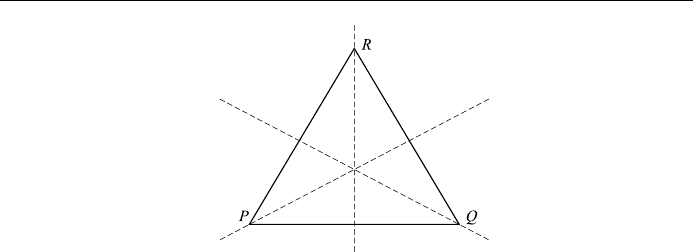
it onto itself. This group contains three elements (see Fig. 12.1):
E08: the identity; triangle is left alone;
A1208: the triangle is rotated through 1208 counterclockwise, which
sends P to Q, Q to R, and R to P;
B2408: the triangle is rotated through 2408 counterclockwise, which
sends P to R, R to Q, and Q to P;
C3608: the triangle is rotated through 3608 counterclockwise, which
sends P back to P, Q back to Q and R back to R.
Notice that C E. Thus there are only three elements represented by E, A, and B.
This set forms a group of order three under addition. The reader can check that
all four group axioms are satis®ed. It is also obvious that operation B is equiva-
lent to performing operation A twice (2408 1208 1208, and the operation C
corresponds to performing A three times. Thus the elements of the group may be
expressed as the power of the single element A as E, A, A
2
, A
3
E): that is, it is a
cyclic group of order three, an d is generated by the element A.
The cyclic group considered in Example 12.8 is a special case of groups of
transformations (rotations, re¯ection, translations, permutations, etc.), the
groups of particular interest to physicists. A transformation that leaves a physical
system invariant is called a symmetry transformation of the system. The set of all
symmetry transformations of a system is a group, as illustrated by this example.
Group multiplication table
A group of order n has n
2
products. Once the products of all ordered pairs of
elements are speci®ed the struc ture of a group is uniquely determined. It is some-
times convenient to arrange these products in a square array called a group multi-
plication table. Such a table is indicated schematically in Table 12.1. The element
that appears at the intersection of the row labeled A and the column labeled B is
the pro duct AB, (in the table A
2
means AA, etc). It should be noted that all the
434
ELEMENTS OF GROUP THEORY
Figure 12.1.
elements in each row or column of the group multiplication must be distinct: that
is, each element appears once and only once in each row or column. This can be
proved easily: if the same element appeared twice in a given row, the row labeled
A say, then there would be two distinct elements C and D such that AC AD.If
we multiply the equation by A
ÿ1
on the left, then we would have A
ÿ1
AC
A
ÿ1
AD,orEC ED. This cannot be true unless C D, in contradiction to
our hypothesis that C and D are distinct. Similarly, we can prove that all the
elements in any column must be distinct.
As a simple practice, consider the group C
3
of Example 12.6 and label the
elements as follows
123!E; 231!X; 312!Y:
If we label the columns of the table with the elements E, X, Y and the rows with
their respective inverses, E, X
ÿ1
, Y
ÿ1
, the group multiplication table then takes
the form shown in Table 12.2.
Isomorphic groups
Two groups are isomorphic to each other if the elements of one group can be put in
one-to-one correspondence with the elements of the other so that the corresponding
elements multiply in the same way. Thus if the elements A; B; C; ...of the group G
435
ISOMORPHIC GROUPS
Table 12.1. Group multiplication table
EA B C ...
EEABC...
AAA
2
AB AC ...
BBBAB
2
BC ...
C C CA CB C
2
...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Table 12.2.
EX Y
EEXY
X
ÿ1
X
ÿ1
E X
ÿ1
Y
Y
ÿ1
Y
ÿ1
Y
ÿ1
X E
