Chow T.L. Mathematical Methods for Physicists: A Concise Introduction

Подождите немного. Документ загружается.

to transform the second term on the right hand side of Eq. (10.62) and obtain

rÿ

Gr; r

r

dr



r

r

Gr; r

ÿGr; r

r

r

  dS

10:63

rÿ

Gr; r

r

dr





r



Gr; r

ÿGr; r



r





 dS

; 10:64

where n

is the outward normal to dS

. The Green's function Gr; r

 can be found

from Eq. (10.60) subject to the appropriate boundary conditions.

If the potential  vanishes on the surface S

or @=@n

vanishes, Eq. (10.64)

reduces to

rÿ

Gr; r

r

dr

: 10:65

On the other ha nd, if the surface S

encloses no charge, then Poisson's equation

reduces to Laplace's equation and Eq. (10.64) reduces to

r



r



Gr; r

ÿGr; r



r





 dS

: 10:66

The potential at a ®eld point r due to a point charge q located at the point r

r

4"

r ÿ r

Now

r ÿ r



ÿ4r ÿ r



(the proof is left as an exercise for the reader) and it follows that the Green's

function Gr; r

in this case is equal

Gr; r



4"

r ÿ r

If the medium is bounded, the Green's function can be obtained by direct solution

of Eq. (10.60) subject to the appropriate boundary conditions.

To illustrate the procedure of the Green's function technique, let us consider a

simple example that can easily be solved by other methods. Consider two

grounded parallel conducting plates of in®nite extent: if the electric charge density

 between the two plates is given, ®nd the electric potential distribution  between

406

PARTIAL DIFFERENTIAL EQUATIONS

the plates. The electric potential distribution  is described by solving Poisson's

equation

 ÿ="

subject to the boundary conditions

(1) 00;

(2) 10:

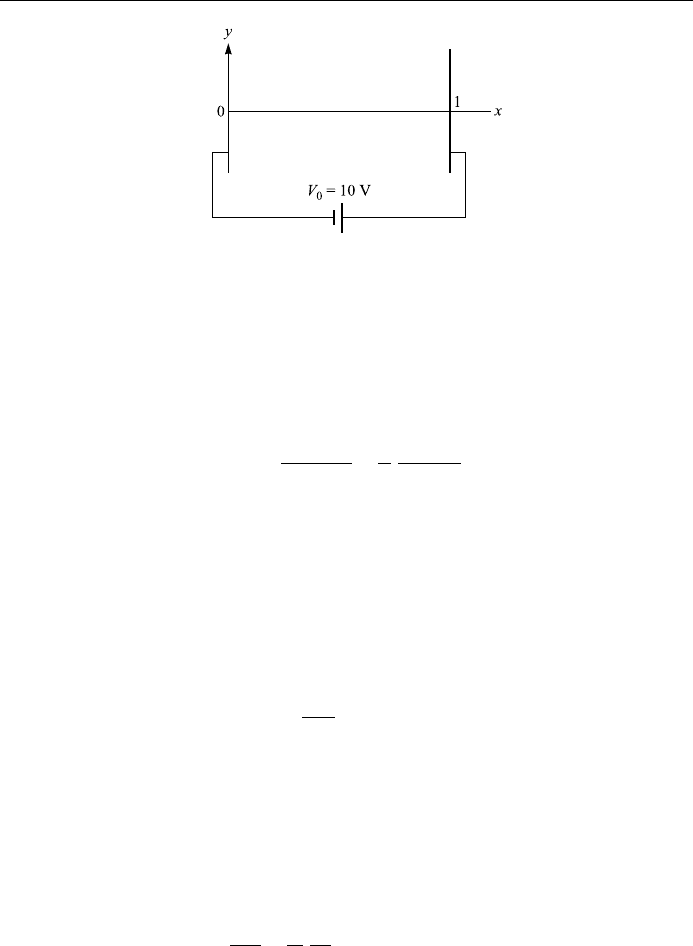
We take the coo rdinates shown in Fig. 10.3. Poisson' s equation reduces to the

simple form



ÿ



: 10:67

Instead of using the general result (10.64), it is more convenient to proceed

directly. Multiplying Eq. (10.67) by Gx; x

 and integrating, we obtain



dx ÿ

xG

dx: 10:68

Then using integration by parts gives



dx  Gx; x



dx

d

and using integration by parts again on the right hand side, we obtain



dx ÿGx; x



dx





 G0; x



d0

ÿ G1; x



d1



dx:

407

SOLUTIONS OF POISSON'S EQUATION

Figure 10.3.

Substituting this into Eq. (10.68) we obtain

G0; x



d0

ÿ G1; x



d1



dx 

Gx; x

x



dx  G1; x



d1

ÿ G0; x



d0

Gx; x

x

dx: 10:69

We must now choose a Green's function which satis®es the following equation

and the boundary cond itions:

ÿx ÿ x

; G0; x

G1; x

0: 10:70

Combining these with Eq. (10.69) we ®nd the solution to be

x



xGx; x

dx: 10:71

It remains to ®nd Gx; x

. By integration, we obtain from Eq. (10.70)

ÿ

 x ÿ x

dx  a ÿUx ÿ x

a;

where U is the unit step function and a is an integration constant to be determined

later. Integrating once we get

Gx; x

ÿ

Ux ÿ x

dx  ax  b ÿx ÿ x

Ux ÿ x

ax  b:

Imposing the boundary conditions on this general solution yields two equations:

G0; x

x

Uÿx

a  0  b  0  0  b  0;

G1; x

ÿ1 ÿ x

U1 ÿ x

a  b  0:

From these we ®nd

a 1 ÿ x

U1 ÿ x

; b  0

and the Green's function is

Gx; x

ÿx ÿ x

Ux ÿ x

1 ÿ x

x: 10:72

This gives the response at x

due to a unit source at x. Interchanging x and x

Eqs. (10.70) and (10.71) we ®nd the solut ion of Eq. (10.67) to be

x

x

Gx

; xdx



x

ÿx

ÿ xUx

ÿ x1 ÿ xx

dx

10:73

408

PARTIAL DIFFERENTIAL EQUATIONS

Note that the Green's function in the last equation can be written in the form

Gx; x



1 ÿ xxx< x

1 ÿ xx

x > x

(

Laplace transform solutions of boundary-value problems

Laplace and Fourier transforms are useful in solving a variety of partial diÿer-

ential equations, the choice of the appropriate transforms depends on the type of

boundary conditions imposed on the problem. To illustrate the use of the Lapace

transforms in solving boundary-value problems, we solve the following equation:

 2

; 10:74

u0; tu3; t0; u x; 010 sin 2x ÿ 6 sin 4x: 10:75

Taking the Laplace transform of Eq. (10.74) with respect to t gives



 2L

Now



 pL uÿux; 0

and



ÿpt

dt 

ÿpt

ux; tdt 

Lu:

Here @

=@x

and

dt are interchangeable because x and t are independent.

For convenience, let

U  Ux; pLux; t 

ÿpt

ux; tdt:

We then have

pU ÿ ux; 02

;

from which we obtain, on using the given condition (10.75),

pU  3 sin 4x ÿ 5 sin 2x: 10:76

409

BOUNDARY-VALUE PROBLEMS

Now think of this as a diÿerential equation in terms of x,withp as a parame ter.

Then taking the Laplace transform of the given conditions u0 ; tu3; t0,

we have

Lu0; t  0; Lu3; t  0

U0; p0; U3; p0:

These are the boundary con ditions on Ux; p. Solving Eq. (10.76) subject to these

conditions we ®nd

Ux; p

5 sin 2x

p  16

3 sin 4x

p  64

The solution to Eq. (10.74) can now be obtained by taking the inverse Laplace

transform

ux; tL

ÿ1

Ux; p  5e

ÿ16

sin 2x ÿ 3e

ÿ64

sin 4x:

The Fourier transform method was used in Chapter 4 for the solution of

ordinary linear ordinary diÿerential equations with constant coecients. It can

be extended to solve a variety of partial diÿerential equations. However, we shall

not discuss this here. Also, there are other methods for the solution of linear

partial diÿerential equations. In general, it is a dicult task to solve partial

diÿerential equations analytically, and very often a numerical method is the

best way of obtaining a solution that satis®es given boundary conditions.

Problems

10.1 (a) Show that yx; tF2x  5tG2x ÿ 5t is a general solution of

 25

(b) Find a particular solution satisfying the conditions

y0; ty; t0; yx; 0sin 2x; y

x; 00:

10.2. State the nature of each of the following equations (that is, whether elliptic,

parabolic, or hyperbolic)

a

 

 0; b x

 y

 3y

10.3 The electromagnetic wave equation: Classical electromagnetic theory was

worked out experimentally in bits and pieces by Coulomb, Oersted, Ampere,

Faraday and many others, but the man who put it all togeth er and built it

into the compact and consistent theory it is today was James Clerk Maxwell.

410

PARTIAL DIFFERENTIAL EQUATIONS

His work led to the understanding of electromagnetic radiation, of which

light is a special case.

Given the four Maxwell equations

rE  ="

; Gauss' law;

rB  

j  "

@E=@tAmpere's law;

rB  0 Gauss' law;

rE ÿ@B=@t Faraday's law;

where B is the magnetic induction, j  v is the current density, and 

is the

permeability of the medium, show that:

(a) the electric ®eld and the magnetic induction can be expressed as

E ÿr ÿ @A=@t; B rA;

where A is called the vector potential, and  the scalar potential. It

should be noted that E and B are invariant under the following trans-

formations:

 A r; 

  ÿ @=@t

in which  is an arbitrary real function. That is, both (A

;, and

;

) yield the same E and B. Any condition which, for computa tional

convenience, restricts the form of A and  is said to de®ne a gauge. Thus

the above transformation is called a gauge transformation and  is

called a gauge parameter.

(b) If we impose the so-called Lorentz gauge condition on A and :

rA  

@=@t0;

then both A and  satisfy the following wave equations:

A ÿ 

ÿ

 ÿ 



ÿ="

10.4 Given Gauss' law

E  ds  q=", ®nd the electric ®eld produced by a

charged plane of in®nite extension is given by E  =", where  is the charge

per unit area of the plane.

10.5 Consider an in®nitely long uncharged conducting cylinder of radius l placed

in an originally uniform electric ®eld E

directed at right angles to the axis of

the cylinder. Find the potential at a point > l from the axis of the cylin-

der. The boundary conditions are:

411

PROBLEMS

; '

ÿE

 cos ' ÿE

x for  !1;

0for  l;



where the x-axis has been taken in the direction of the uniform ®eld E

10.6 Obtain the solution of the heat conduction equation

ux; t





@ux; t

which satis®es the bounda ry conditions

(1) u0; tul; t0; t  0; (2) ux; 0f x; 0  x, where f x is a

given function and l is a constant.

10.7 If a battery is connected to the plates as shown in Fig. 10.4, and if the charge

density distribution between the two plates is still given by x, ®nd the

potential distribution between the plates.

10.8 Find the Green's function that satis®es the equation

 x ÿ x



and the boundary conditions G  0 when x  0 and G remains bounded

when x approaches in®nity. (This Green's function is the potential due to a

surface charge ÿ" per unit area on a plane of in®nite extent located at x  x

in a dielectric medium of permittivity " when a grounded conducting plane

of in®nite extent is located at x  0.)

10.9 Solve by Laplace transforms the boundary-value problem



for x > 0; t > 0;

given that u  u

(a constant) on x  0 for t > 0, and u  0 for x > 0; t  0.

412

PARTIAL DIFFERENTIAL EQUATIONS

Figure 10.4.

Simple linear integral equations

In previous chapters we have met equations in which the unknown functions

appear under an integral sign. Such equations are called integral equations.

Fourier and Laplace transforms are important integral equations, In Chapter 4,

by introducing the method of Green's function we were led in a natural way to

reformulate the problem in terms of integral equations. Integral equations have

become one of the very useful and sometimes indispensable mathematical tools of

theoretical physics and engineering.

Classi®cation of linear integral equations

In this chapter we shall con®ne our attention to linear integral equations. Linear

integral equations can be divided into two major groups:

(1) If the unknown function occurs only under the integral sign, the integral

equation is said to be of the ®rst kind. Integral equations having the

unknown function both inside and outside the integral sign are of the second

kind.

(2) If the limits of integration are constants, the equation is called a Fredholm

integral equation. If one limit is variable, it is a Volterra equation.

These four kinds of linear integral equations can be written as follows:

f x

Kx; tutdt Fredholm equation of the first kind; 11:1

uxf x

Kx; tutdt Fredholm equation of the second kind;

11:2

413

f x

Kx; tu t dt Volterra equation of the first kin d; 11:3

uxf x

Kx; tutdt Volterra equation of the second kind:

11:4

In each case ut is the unknown function, K x; t and f x are assumed to be

known. Kx; t is called the kernel or nucleus of the integral equation.  is a

parameter, which often plays the role of an eigenvalue. The equation is said to

be homogen eous if f x0.

If one or both of the limits of integration are in®nite, or the kernel Kx; t

becomes in®nite in the range of integration, the equation is said to be singular;

special techniques are required for its solut ion.

The general linear integral equation may be written as

hxuxf x

Kx; tutdt: 11:5

If hx0, we have a Fredholm equation of the ®rst kind; if hx1, we have a

Fredholm equation of the second kind. We have a Volterra equatio n when the

upper limit is x.

It is beyond the scope of this book to present the purely mathematical general

theory of these various types of equations. After a general discussion of a few

methods of solution, we will illustrate them with some simple examples. We will

then show with a few examples from physical problems how to convert diÿerential

equations into integral equations.

Some methods of solution

Separable kernel

When the two variables x and t which appear in the kernel Kx; t are separable,

the problem of solving a Fr edholm equation can be reduced to that of solving a

system of algebraic equations, a much easier task. When the kernel Kx; t can be

written as

Kx; t

i1

xh

t; 11:6

where gx is a function of x only and ht a function of t only, it is said to be

degenerate. Putting Eq. (11.6) into Eq. (11.2), we obtain

uxf x

i1

xh

tutdt:

414

SIMPLE LINEAR INTEGRAL EQUATIONS

Note that gx is a constant as far as the t integration is concerned, hence it may

be taken outside the integral sign and we have

uxf x

i1

x

tutdt: 11:7

Now

tutdt  C

 const:: 11:8

Substituting this into Eq. (11.7) and solving for ut, we obtain

utf xC

i1

x: 11:9

The value of C

may now be obtained by substituting Eq. (11.9) into Eq. (11.8).

The solution is only valid for certa in values of , and we call these the eigenvalues

of the integral equation. The homogeneous equation has non-trivial solutions

only if  is one of these eigenvalues; these solutions are called eigenf unctions of

the kernel (operator) K.

Example 11.1

As an example of this method, we consider the following equation:

uxx  

xt

 x

tutdt: 11:10

This is a Fredholm equation of the second kind, with f xx and

Kx; txt

 x

t. If we de®ne

 

utdt;ÿ

tutdt; 11:11

then Eq. (11.10) becomes

uxx  x  ÿx

: 11:12

To determine A and B, we put Eq. (11.12) back into Eq. (11.11) and obtain

 



 

ÿ; ÿ 



 

ÿ: 11:13

Solving this for  and ÿ we ®nd

 

60  

240 ÿ 120 ÿ 

;ÿ

240 ÿ 120 ÿ 

;

and the ®nal solution is

ut

240 ÿ 60x  80x

240 ÿ 120 ÿ 

415

SOME METHODS OF SOLUTION