Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


The ®rst equation is ready for integration. Do you recognize the
second equation in as Legendre's equation? (Compare it with Eq.
(7.30).) If you are unsure, try to simplify it by putting ÿ 2m=p;
2mþ=p
1=2
, and you will obtain
sin
d
d
sin
d
d
ÿ sin
2
ÿ
2
0
or
1
sin
d
d
sin
d
d
ÿ ÿ
2
sin
2
0;
which more closely resembles Eq. (7.30).
7.23 Consider the diÿerential equation
y
00
Rxy
0
QxPxy 0:
Show that it can be put into the form of the Sturm ±Liouville equation
(7.104) with
rxe
R
Rxdx
; qxQxe
R
Rxdx
; and pxPxe
R
Rxdx
:
7.24. (a) Show that the system y
00
y 0; y00; y10 is a Sturm±
Liouville system.
(b) Find the eigenvalues and eigenfunctions of the system.
(c) Prove that the eigenfunctions are orthogonal on the interval 0 x 1.
(d) Find the corresponding set of normalized eigenfunctions, and expand
the function f x1 in a series of these orthonormal functions.
346
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS

8
The calculus of variations
The calculus of variations, in its present form, provides a powerful method for the
treatment of variational principles in physics and has become increasingly impor-
tant in the development of modern physics. It is originated as a study of certain
extremum (maximum and minimum) problems not treatable by elementary
calculus. To see this more precisely let us consider the following integral whose
integrand is a function of x, y, and of the ®rst derivative y
0
xdy=dx:
I
Z
x
2
x
1
fyx; y
0
x; x
þ
dx; 8:1
where the semicolon in f separates the independent variable x from the dependent
variable yx and its deriva tive y
0
x. For what function yx is the value of the
integral I a maximum or a minimum? This is the basic problem of the calculus of
variations.
The quantity f depends on the functional form of the dependent variable yx
and is called the functional whi ch is considered as given, the limits of integration
are also given. It is also understood that y y
1
at x x
1
, y y
2
at x x
2
.In
contrast with the simple extreme-value problem of diÿerential calculus, the func-
tion yx is not known here, but is to be varied until an extreme value of the
integral I is found. By this we mean that if yx is a curve which gives to I a
minimum value, then any neighboring curve will make I increase.
We can make the de®nition of a neighboring curve clear by giving yx a
parametric representation:
y"; xy0; x"x; 8:2
where x is an arbitrary function which has a continuous ®rst derivative and " is
a small arbitrary parameter. In order for the curve (8.2) to pass through x
1
; y
1
and x
2
; y
2
, we require that x
1
x
2
0 (see Fig. 8.1). Now the integral I
347
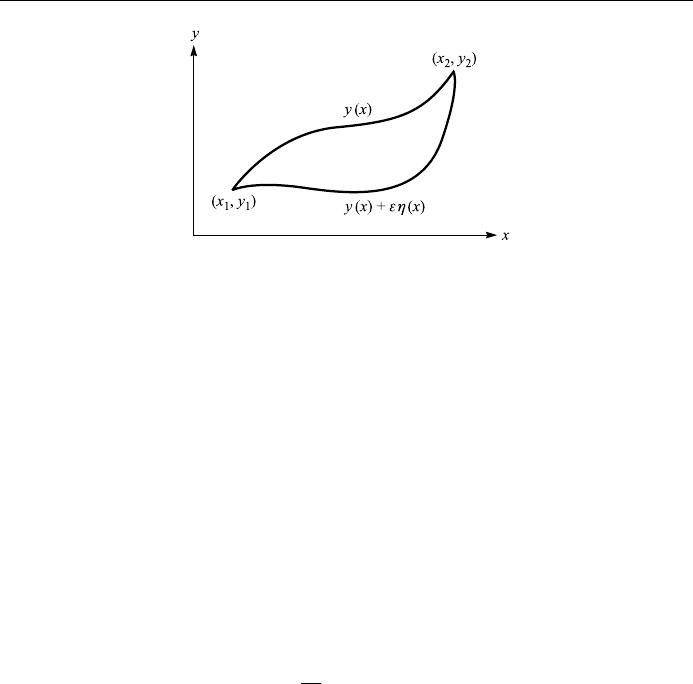
also becomes a function of the parameter "
I"
Z
x
2
x
1
f fy"; x; y
0
"; x; xgdx: 8:3
We then require that yxy0; x makes the integral I an extreme, that is, the
integral I" has an extreme value for " 0:
I"
Z
x
2
x
1
f fy"; x; y
0
"; x; xgdx extremum for " 0:
This gives us a very simple method of determining the extreme value of the
integral I. The necessary condition is
dI
d"
ý
ý
ý
ý
"0
0 8:4
for all functions x. The sucient conditions are quite involved and we shall
not pursue them. The interested reader is referred to mathematical texts on the
calculus of variations.
The problem of the extreme-value of an integral occurs very often in geometry
and physics. The simplest example is provided by the problem of determining the
shortest curve (or distance) between two given points. In a plane, this is the
straight line. But if the two given points lie on a given arbitrary surface, then
the analytic equation of this curve, which is called a geodesic, is found by solution
of the above extreme-value problem.
The Euler±Lagrange equation
In order to ®nd the required curve yx we carry out the indicated diÿerentiation
in the extremum condition (8.4):
348
THE CALCULUS OF VARIATIONS
Figure 8.1.

@I
@"
@
@"
Z
x
2
x
1
f fy"; x; y
0
"; x; xgdx
Z
x
2
x
1
@f
@y
@y
@"
@f
@y
0
@y
0
@"
dx; 8:5
where we have employed the fact that the limits of integration are ®xed, so the
diÿerential operation aÿects only the integrand. From Eq. (8.2) we have
@y
@"
x and
@y
0
@"
d
dx
:
Substituting these into Eq. (8.5) we obtain
@I
@"
Z
x
2
x
1
@f
@y
x
@f
@y
0
d
dx
dx: 8:6
Using integration by parts, the second term on the right hand side becomes
Z
x
2
x
1
@f
@y
0
d
dx
dx
@f
@y
0
x
ý
ý
ý
ý
x
2
x
1
ÿ
Z
x
2
x
1
d
dx
@f
@y
0
xdx:
The integrated term on the right hand side vanishes because x
1
x
2
0
and Eq. (8.6) becomes
@I
@"
Z
x
2
x
1
@f
@y
@y
@"
ÿ
d
dx
@f
@y
0
@y
@"
dx
Z
x
2
x
1
@f
@y
ÿ
d
dx
@f
@y
0
x dx: 8:7
Note that @f =@y and @f =@y
0
are still functions of ". However, when
" 0; y"; xyx and the dependence on " disappears.
Then @I=@"j
"0
vanishes, and since x is an arbitrary function, the inte-
grand in Eq. (8.7) must vanish for " 0:
d
dx
@f
@y
0
ÿ
@f
@y
0: 8:8
Eq. (8.8) is known as the Euler±Lagrange equation; it is a necessary but not
sucient condition that the integral I have an extreme value. Thus, the solution
of the Euler±Lagrange equation may not yield the minimizing curve. Ordinarily
we must verify whether or not this solution yields the curve that actually mini-
mizes the integral, but frequently physical or geometrical considerations enable us
to tell whether the curve so obtained makes the integ ral a minimum or a max-
imum. The Euler±Lagrange equation can be written in the form (Problem 8.2)
d
dx
f ÿ y
0
@f
@y
0
ÿ
@f
@x
0: 8:8a
349
THE EULER±LAGRANGE EQUATION
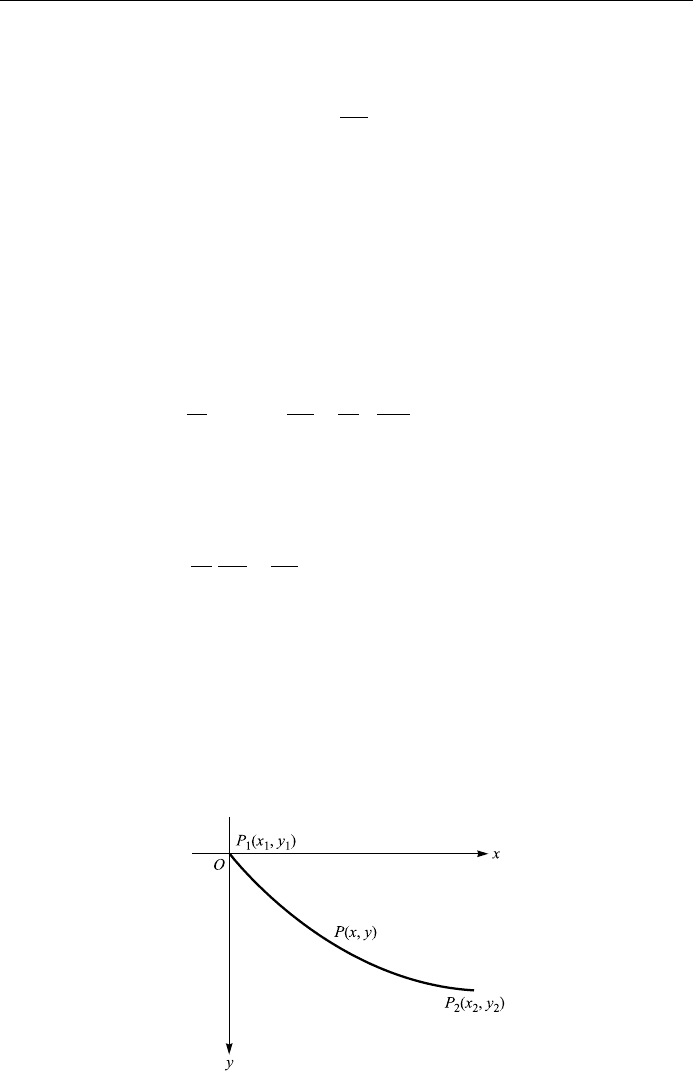
This is often called the second form of the Euler±Lag range equation. If f does not
involve x explicitly, it can be integrated to yield
f ÿ y
0
@f
@y
0
c; 8:8b
where c is an integration constant.
The Euler±Lagrange equati on can be extended to the case in which f is a
functional of several dependent variables:
f fy
1
x; y
0
1
x; y
2
x; y
0
2
x; ...;x
þ
:
Then, in analogy wi th Eq. (8.2), we now have
y
i
"; xy
i
0; x"
i
x; i 1; 2; ...; n:
The development proceeds in an exactly analogous manner, with the result
@I
@"
Z
x
2
x
1
@f
@y
i
ÿ
d
dx
@f
@y
i
0
i
xdx:
Since the individual variations, that is, the
i
x, are all independent, the vanish-
ing of the above equation when evaluated at " 0 requires the separate vanishing
of each expression in the brackets:
d
dx
@f
@y
0
i
ÿ
@f
@y
i
0; i 1; 2; ...; n: 8:9
Example 8.1
The brachistochrone problem: Historically, the brachistochrone problem was the
®rst to be treated by the method of the calculus of variations (®rst solved by
Johann Ber noulli in 1696). As shown in Fig. 8.2, a particle is constrained to
move in a gravitational ®eld starting at rest from some point P
1
to some lower
350
THE CALCULUS OF VARIATIONS
Figure 8.2

point P
2
. Find the shape of the path such that the particle goes from P
1
to P
2
in
the least time. (The word brachistochrone was derived from the Greek brachistos
(shortest) and chronos (time).)
Solution: If O and P are not very far apart, the gravitational ®eld is constant, and
if we ignore the possibility of friction, then the total energy of the particle is
conserved:
0 mgy
1
1
2
m
ds
dt
2
mgy
1
ÿ y;
where the left hand side is the sum of the kinetic energy and the potential energy
of the particle at point P
1
, and the right hand side refers to point Px; y. Solving
for ds=dt:
ds=dt
2gy
p
:
Thus the time required for the particle to move from P
1
to P
2
is
t
Z
P
2
P
1
dt
Z
P
2
P
1
ds
2gy
p
:
The line element ds can be expressed as
ds
dx
2
dy
2
q
1 y
02
q
dx; y
0
dy=dx;
thus, we have
t
Z
P
2
P
1
dt
Z
P
2
P
1
ds
2gy
p
1
2g
p
Z
x
2
0
1 y
02
p
y
p
dx:
We now ap ply the Euler±Lagrange equation to ®nd the shape of the path for
the particle to go from P
1
to P
2
in the least time. The con stant doe s not aÿect the
®nal equation and the functional f may be identi®ed as
f
1 y
02
q
=
y
p
;
which does not involve x explicitly. Using Problem 8.2(b), we ®nd
f ÿ y
0
@f
@y
0
1 y
02
p
y
p
ÿ y
0
y
0
1 y
02
p
y
p
"#
c;
which simpli®es to
1 y
02
q
y
p
1=c:
351
THE EULER±LAGRANGE EQUATION
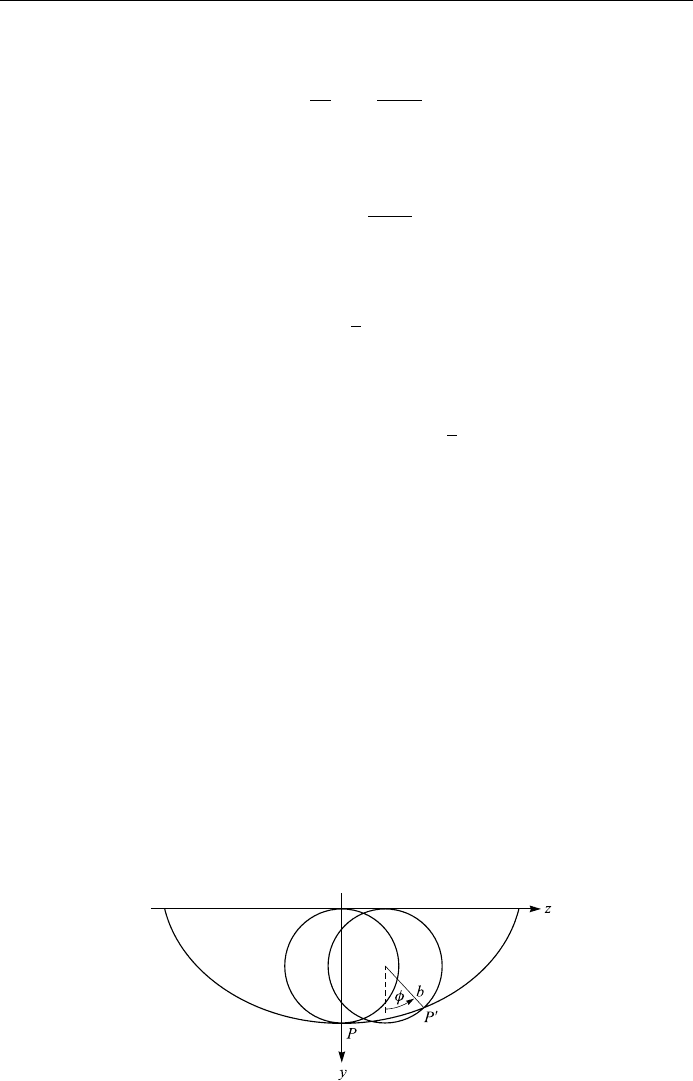
Letting 1=c
a
p
and solving for y
0
gives
y
0
dy
dx
a ÿ y
y
r
;
and solving for dx and integrating we obtain
Z
dx
Z
y
a ÿ y
r
dy:
We then let
y a sin
2
a
2
1 ÿ cos 2
which leads to
x 2a
Z
sin
2
d a
Z
1 ÿ cos 2d
a
2
2 ÿ sin 2k:
Thus the parametric equation of the path is given by
x b1 ÿ cos ; y b ÿ sin k;
where b a = 2; 2. The path passes through the origin so we have k 0 and
x b1 ÿ cos ; y b ÿ sin :
The constant b is determined from the condition that the particle passes through
P
2
x
2
; y
2
:
The required path is a cycloid and is the path of a ®xed point P
0
on a circle of
radius b as it rolls along the x-axis (Fig. 8.3).
A line that represents the shortest path between any two points on some surface
is called a geodesic. On a ¯at surface, the geodesic is a straight line. It is easy to
show that, on a sphere, the geodesic is a great circle; we leave this as an exercise
for the reader (Problem 8.3).
352
THE CALCULUS OF VARIATIONS
Figure 8.3.

Variational problems with constraints
In certain problems we seek a minimum or maximum value of the integ ral (8.1)
I
Z
x
2
x
1
fyx; y
0
x; x
þ
dx 8:1
subject to the condition that another integral
J
Z
x
2
x
1
gyx; y
0
x; x
þ
dx 8:10
has a known constant value. A simple problem of this sort is the problem of
determining the curve of a given perimeter which e ncloses the largest area, or
®nding the shape of a chain of ®xed length which minimizes the potential energy.
In this case we can use the method of Lagrange multipliers which is based on
the following theorem:
The problem of the stationary value of F(x, y) subject to the con-
dition Gx; yconst. is equivalent to the problem of stationa ry
values, without constraint, of F G for some constant , pro-
vided either @G =@x or @G=@y does not vanish at the critical point.
The constant is called a Lagrange multiplier and the method is known as the
method of Lagrange multipliers. To see the ideas behind this theorem, let us
assume that Gx; y 0 de®nes y as a unique function of x, say, y gx, having
a continuous derivative g
0
x. Then
Fx; yFx; gx
and its maximum or minimum can be found by setting the derivative with respect
to x equal to zero:
@F
@x
@F
@y
dy
dx
0orF
x
F
y
g
0
x0: 8:11
We also have
Gx; gx 0;
from which we ®nd
@G
@x
@G
@y
dy
dx
0orG
x
G
y
g
0
x0: 8:12
Eliminating g
0
x between Eq. (8.11) and Eq. (8.12) we obtain
F
x
ÿ F
y
=G
y
ÿ
G
x
0; 8:13
353
VARIATIONAL PROBLEMS WITH CONSTRAINTS

provided G
y
@G=@y 6 0. De®ning ÿF
y
=G
y
or
F
y
G
y
@F
@y
@G
@y
0; 8:14
Eq. (8.13) becomes
F
x
G
x
@F
@x
@G
@x
0: 8:15
If we de®ne
Hx; yFx; yGx; y;
then Eqs. (8.14) and (8.15) become
@Hx; y=@x 0; Hx; y=@y 0;
and this is the basic idea behind the method of Lagrange multipliers.
It is natural to attempt to solve the problem I minimum subject to the con-
dition J constant by the method of Lagrange multipliers. We construct the
integral
I J
Z
x
2
x
1
Fy; y
0
; xGy; y
0
; xdx
and consider its free extre mum. This implies that the function yx that makes the
value of the integral an extremum must satisfy the equation
d
dx
@F G
@y
0
@F G
@y
0 8:16
or
d
dx
@F
@y
0
ÿ
@F
@y
d
dx
@G
@y
0
ÿ
@G
@y
0: 8:16a
Example 8.2
Isoperimetric problem: Find that curve C having the given perimeter l that
encloses the largest area.
Solution: The area bounded by C can be expressed as
A
1
2
Z
C
xdy ÿ ydx
1
2
Z
C
xy
0
ÿ ydx
and the length of the curve C is
s
Z
C
1 y
02
q
dx l:
354
THE CALCULUS OF VARIATIONS
Then the function H is
H
Z
C
1
2
xy
0
ÿ y
1 y
02
p
dx
and the Euler±Lagrange equation gives
d
dx
1
2
x
y
0
1 y
02
p
ü!
1
2
0
or
y
0
1 y
02
p
ÿx c
1
:
Solving for y
0
, we get
y
0
dy
dx
x ÿ c
1
2
ÿx ÿ c
1
2
q
;
which on integrating gives
y ÿ c
2
2
ÿx ÿ c
1
2
q
or
x ÿ c
1
2
y ÿ c
2
2
2
; a circle:
Hamilton's principle and Lagrange's equation of motion
One of the most important applications of the calculus of variations is in classical
mechanics. In this case, the functional f in Eq. (8.1) is taken to be the Lagrangian
L of a dynamical system. For a conservative system, the Lagrangian L is de®ned
as the diÿerence of kinetic and potential energies of the system:
L T ÿ V;
where time t is the independent variable and the generalized coordinates q
i
t are
the dependent variables. What do we mean by generalized coordinates? Any
convenient set of parameters or quantities that can be used to specify the con®g-
uration (or state) of the system can be assumed to be generalized coordinates;
therefore they need not be geometrical quantities, such as distances or angles. In
suitable circumstances, for example, they could be electric currents.
Eq. (8.1) now takes the form that is known as the action (or the action integral)
I
Z
t
2
t
1
Lq
i
t;
_
q
i
t; tdt;
_
q dq=dt 8:17
355
HAMILTON'S PRINCIPLE
