Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


or
u
00
1
4x
2
1
x
1=2
y u
00
1
4x
2
1
u 0;
the solution of which is
u A cos x B sin x:
Thus the approximate solution to Bessel's equation for very large values of x is
y x
ÿ1=2
A cos x B sin xCx
ÿ1=2
cosx þ:
A more rigorous argument leads to the following asymptotic formula
J
n
x
2
x
1=2
cos x ÿ
4
ÿ
n
2
: 7:94
For very small values of x (that is, near 0), by examining the solution itself and
dropping all terms after the ®rst, we ®nd
J
n
x
x
n
2
n
ÿn 1
: 7:95
Orthogonality of Bessel functions
Bessel functions enjoy a property which is called orthogonality and is of general
importance in mathematical physics. If and are two diÿerent constants, we
can show that under certain conditions
Z
1
0
xJ
n
xJ
n
xdx 0:
Let us see what these conditions are. First, we can show that
Z
1
0
xJ
n
xJ
n
xdx
J
n
J
0
n
ÿJ
n
J
0
n
2
ÿ
2
: 7:96
To show this, let us go back to Bessel's equation (7.71) and change the indepen-
dent variable to x, where is a constant, then the resul ting equation is
x
2
y
00
xy
0
2
x
2
ÿ n
2
y 0
and its general solution is J
n
x. Now suppose we have two such equations, one
for y
1
with constant , and one for y
2
with constant :
x
2
y
00
1
xy
0
1
2
x
2
ÿ n
2
y
1
0; x
2
y
00
2
xy
0
2
2
x
2
ÿ n
2
y
2
0:
Now multiplying the ®rst equation by y
2
, the second by y
1
and subtracting, we get
x
2
y
2
y
00
1
ÿ y
1
y
00
2
xy
2
y
0
1
ÿ y
1
y
0
2
2
ÿ
2
x
2
y
1
y
2
:
336
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS

Dividing by x we obtain
x
d
dx
y
2
y
0
1
ÿ y
1
y
0
2
y
2
y
0
1
ÿ y
1
y
0
2
2
ÿ
2
xy
1
y
2
or
d
dx
fxy
2
y
0
1
ÿ y
1
y
0
2
g
2
ÿ
2
xy
1
y
2
and then integration gives
2
ÿ
2
Z
xy
1
y
2
dx xy
2
y
0
1
ÿ y
1
y
0
2
;
where we have omitted the constant of integration. Now y
1
J
n
x; y
2
J
n
x,
and if 6 we then have
Z
xJ
n
xJ
n
xdx
xJ
n
xJ
0
n
xÿJ
n
xJ
0
n
x
2
ÿ
2
:
Thus
Z
1
0
xJ
n
xJ
n
xdx
J
n
J
0
n
ÿJ
n
J
0
n
2
ÿ
2
q:e:d:
Now letting ! and using L'Hospi tal's rule, we obtain
Z
1
0
xJ
2
n
xdx lim
!
J
0
n
J
0
n
ÿJ
n
J
0
n
ÿJ
n
J
00
n
2
J
0
n
2
ÿJ
n
J
0
n
ÿJ
n
J
00
n
2
:
But
2
J
00
n
J
0
n
2
ÿ n
2
J
n
0:
Solving for J
00
n
and substituting, we obtain
Z
1
0
xJ
2
n
xdx
1
2
J
0
n
2
1 ÿ
n
2
2
ý!
J
2
n
x
"#
: 7:97
Furthermore, if and are any two diÿerent roots of the equation
RJ
n
xSxJ
0
n
x0, where R and S are constant, we then have
RJ
n
SJ
0
n
0; RJ
n
SJ
0
n
0;
from these two equations we ®nd, if R 6 0; S 6 0,
J
n
J
0
n
ÿJ
n
J
0
n
0
337
BESSEL'S EQUATION

and then from Eq. (7.96) we obtain
Z
1
0
xJ
n
xJ
n
xdx 0: 7:98
Thus, the two functions
x
p
J
n
x and
x
p
J
n
x are orthogonal in (0, 1). We can
also say that the two functions J
n
x and J
n
x are orthogonal with respect to
the weighted function x.
Eq. (7.98) is also easily proved if R 0 and S 6 0, or R 6 0 but S 0. In this
case, and can be any two diÿerent roots of J
n
x0orJ
0
n
x0.
Spherical Bessel functions
In physics we often meet the following equation
d
dr
r
2
dR
dr
k
2
r
2
ÿ ll 1R 0; l 0; 1; 2; ...: 7:99
In fact, this is the radial equatio n of the wave and the Helmholtz partial diÿer-
ential equation in the spherical coordinate system (see Problem 7.22). If we let
x kr and yxRr, then Eq. (7.99) be comes
x
2
y
00
2xy
0
x
2
ÿ ll 1y 0 l 0; 1; 2; ...; 7:100
where y
0
dy=dx. This equation almost matches Bessel's equation (7.71). Let us
make the further sub stitution
yxwx=
x
p
;
then we obtain
x
2
w
00
xw
0
x
2
ÿl
1
2
w 0 l 0; 1; 2; ...: 7:101
The reader should recognize this equation as Bessel's equation of order l
1
2
.It
follows that the solutions of Eq. (7.100) can be written in the form
yxA
J
l1=2
x
x
p
B
J
ÿlÿ1=2
x
x
p
:
This leads us to de®ne spherical Bessel functions j
l
xCJ
lE
x=
x
p
. The factor
C is usually chosen to be
=2
p
for a reason to be explained later:
j
l
x
=2x
p
J
l
Ex: 7:102
Similarly, we can de®ne
n
l
x
=2x
p
N
lE
x:
338
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS

We can express j
l
x in terms of j
0
x. To do this, let us go back to J
n
x and we
®nd that
d
dx
fx
ÿn
J
n
xg ÿx
ÿn
J
n1
x; or J
n1
xÿx
n
d
dx
fx
ÿn
J
n
xg:
The proof is simple and straightforward:
d
dx
fx
ÿn
J
n
xg
d
dx
X
1
k0
ÿ1
k
x
2k
2
n2k
k!ÿn k 1
x
ÿn
X
1
k0
ÿ1
k
x
n2kÿ1
2
n2kÿ1
k ÿ 1!ÿn k 1
x
ÿn
X
1
k0
ÿ1
k1
x
n2k1
2
n2k1
k!ÿn k 2g
ÿx
ÿn
J
n1
x:
Now if we set n l
1
2
and divide by x
l3=2
, we obtain
J
l3=2
x
x
l3=2
ÿ
1
x
d
dx
J
l1=2
x
x
l1=2
or
j
l1
x
x
l1
ÿ
1
x
d
dx
j
l
x
x
l
:
Starting with l 0 and applying this formula l times, we obtain
j
l
xx
l
ÿ
1
x
d
dx
l
j
0
xl 1 ; 2; 3; ...: 7:103
Once j
0
x has been chosen, all j
l
x are uniquely determined by Eq. (7.103).
Now let us go back to Eq. (7.102) and see why we chose the constant factor C to
be
=2
p
. If we set l 0 in Eq. (7.101), the resulting equation is
xy
00
2y
0
xy 0:
Solving this equation by the power series method, the reader will ®nd that func-
tions sin (x=x and cos (x=x are among the solutions. It is customary to de®ne
j
0
xsinx=x:
Now by using Eq. (7.76), we ®nd
J
1=2
x
X
1
k0
ÿ1
k
x=2
1=22k
k!ÿk 3=2
x=2
1=2
1=2
p
1 ÿ
x
2
3!
x
4
5!
ÿ
ý!
x=2
1=2
1=2
p
sin x
x
2
x
r
sin x:
Comparing this with j
0
x shows that j
0
x
=2x
p
J
1=2
x, and this explains the
factor
=2
p
chosen earlier.
339
SPHERICAL BESSEL FUNCTIONS

Sturm±Liouville systems
A boundary-value problem having the form
d
dx
rx
dy
dx
qxpxy 0; a x b 7:104
and satisfying boundary conditions of the form
k
1
yak
2
y
0
a0; l
1
ybl
2
y
0
b0 7:104a
is called a Sturm±Liouville boundary-value problem; Eq. (7.104) is known as the
Sturm±Liouville equation. Legendre's equation, Bessel's equation and many other
important equations can be written in the form of (7.104).
Legendre's equation (7.1) can be written as
1 ÿ x
2
y
0
0
y 0; 1;
we can then see it is a Sturm±Liouville equation with r 1 ÿ x
2
; q 0 and p 1.
Then, how do Bessel functions ®t into the Sturm±Liouville framework? Js
satis®es the Bessel equation (7.71)
s
2
J
n
s
_
J
n
s
2
ÿ n
2
J
n
0;
_
J
n
dJ
n
=ds: 7:71a
We assume n is a positive integer and setting s x, with a non-zero constant,
we have
ds
dx
;
_
J
n
dJ
n
dx
dx
ds
1
dJ
n
dx
;
J
n
d
dx
1
dJ
n
dx
dx
ds
1
2
d
2
J
n
dx
2
and Eq. (7.71a) becomes
x
2
J
00
n
xxJ
0
n
x
2
x
2
ÿ n
2
J
n
x0; J
0
n
dJ
n
=dx
or
xJ
00
n
xJ
0
n
x
2
x ÿ n
2
=xJ
n
x0;
which can be written as
xJ
0
n
x
0
ÿ
n
2
x
2
x
ý!
J
n
x0:
It is easy to see that for each ®xed n this is a Sturm±Liouville equation (7.104),
with rxx, qxÿn
2
=x; pxx, and with the parameter now written as
2
.
For the Sturm±Liouville system (7.104) and (7.104a), a non-trivial solution
exists in general only for a particular set of values of the parameter . These
values are called the eigenvalues of the system. If rx and qx are real, the
eigenvalues are real. The corresponding solutions are called eigenfunctions of
340
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS

the system. In general there is one eigenfunction to each eigenvalue. This is the
non-degenerate case. In the degenerate case, more than one eigenfunction may
correspond to the same eigenvalue. The eigenfunctions form an orthogonal set
with respect to the density function px which is generally 0.Thus by suitable
normalization the set of functions can be made an orthonormal set with respect to
px in a x b. We now proceed to prove these two general claims.
Property 1
If rx and qx are real, the eigenva lues of a Sturm±Liouville
system are real.
We start with the Sturm±Liouville equation (7.104) and the boundary condi-
tions (7.104a):
d
dx
rx
dy
dx
qxpx y 0; a x b;
k
1
yak
2
y
0
a0; l
1
ybl
2
y
0
b0;
and assume that rx; qx; px; k
1
; k
2
; l
1
,andl
2
are all real, but and y may be
complex. Now take the complex conjugates
d
dx
rx
d
y
dx
qx
px
y 0 ; 7:105
k
1
yak
2
y
0
a0; l
1
ybl
2
y
0
b0; 7:105a
where
y and
are the complex conjugates of y and , respectively.
Multiplying (7.1 04) by
y, (7.105) by y, and subtracting, we obtain after
simplifying
d
dx
rxy
y
0
ÿ
yy
0
ÿ
pxy
y:
Integrating from a to b, and using the boundary conditions (7.104a) a nd (7.105a),
we then obtain
ÿ
Z
b
a
px y
0
þ
þ
þ
þ
2
dx rxy
y
0
ÿ
yy
0
j
b
a
0:
Since px0ina x b, the integral on the left is positive and therefore
, that is, is real.
Property 2
The eigenfunctions corresponding to two diÿerent eigenvalues
are orthogonal with respect to px in a x b.
341
STURM±LIOUVILLE SYSTEMS

If y
1
and y
2
are eigenfunctions corresponding to the two diÿerent eigenvalues
1
;
2
, respectively,
d
dx
rx
dy
1
dx
qx
1
pxy
1
0; a x b; 7:106
k
1
y
1
ak
2
y
0
1
a0; l
1
y
1
bl
2
y
0
1
b0; 7:106a
d
dx
rx
dy
2
dx
qx
2
pxy
2
0; a x b; 7:107
k
1
y
2
ak
2
y
0
2
a0; l
1
y
2
bl
2
y
0
2
b0: 7:107a
Multiplying (7.106) by y
2
and (7.107) by y
1
, then subtracting, we obtain
d
dx
rxy
1
y
0
2
ÿ y
2
y
0
1
ÿ
pxy
1
y
2
:
Integrating from a to b, and using (7.10 6a) and (7.107a), we obtain
1
ÿ
2
Z
b
a
pxy
1
y
2
dx rxy
1
y
0
2
ÿ y
2
y
0
1
j
b
a
0:
Since
1
6
2
we have the required result; that is,
Z
b
a
pxy
1
y
2
dx 0 :
We can normalize these eigenfunctions to make them an orthonormal set, and
so we can expand a given function in a series of these orthonormal eigenfunctions.
We have shown that Legendre's equati on is a Sturm±Liouville equation with
rx1 ÿ x; q 0 and p 1. Since r 0 when x 1, no boundary conditions
are needed to form a Sturm ±Liouville problem on the interval ÿ1 x 1. The
numbers
n
nn 1 are eigenvalues with n 0; 1; 2; 3; .... The corresponding
eigenfunctions are y
n
P
n
x. Property 2 tells us that
Z
1
ÿ1
P
n
xP
m
xdx 0 n 6 m:
For Bessel functions we saw that
xJ
0
n
x
0
ÿ
n
2
x
2
x
ý!
J
n
x0
is a Sturm±Liouville equation (7.104), with r xx; q xÿn
2
=x; pxx, and
with the parameter now written as
2
. Typically, we want to solve this equation
342
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS

on an interval 0 x b sub ject to
J
n
b0:
which lim its the selection of . Property 2 then tells us that
Z
b
0
xJ
n
k
xJ
n
l
xdx 0; k 6 l:
Problems
7.1 Using Eq. (7.11), show that P
n
ÿxÿ1
n
P
n
x and P
n
0
ÿx
ÿ1
n1
P
0
n
x:
7.2 Find P
0
x; P
1
x; P
2
x; P
3
x, and P
4
x from Rodrigues' formula (7.12).
Compare yo ur results with Eq. (7.11).
7.3 Establish the recurrence formula (7.16b) by manipulating Rodrigues'
formula.
7.4 Prove that P
0
5
x9P
4
x5P
2
xP
0
x.
Hint: Use the recurrence relation (7.16d).
7.5 Let P and Q be two points in space (Fig. 7.6). Using Eq. (7.14), show that
1
r
1
r
2
1
r
2
2
ÿ 2r
1
r
2
cos
q
1
r
2
P
0
P
1
cos
r
1
r
2
P
2
cos
r
1
r
2
2
"#
:
7.6 What is P
n
1? What is P
n
ÿ1?
7.7 Obtain the associated Legendre functi ons: a P
1
2
x; b P
2
3
x; c P
3
2
x:
7.8 Verify that P
2
3
x is a solution of Legendre's associated equation (7.25) for
m 2, n 3.
7.9 Verify the orthogonality conditions (7.31) for the functions P
1
2
x and P
1
3
x.
343
PROBLEMS
Figure 7.6.
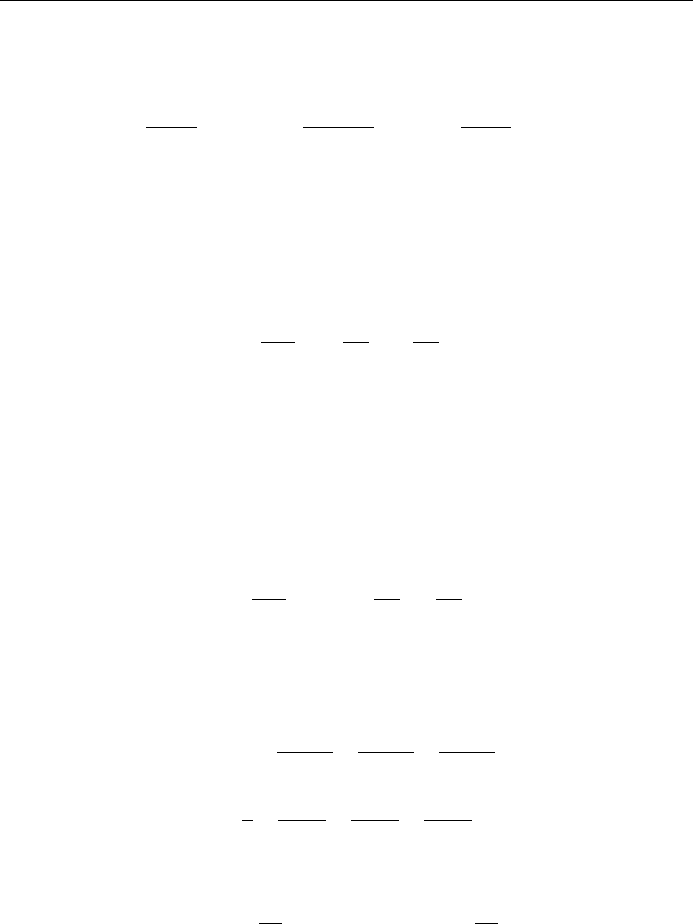
7.10 Verify Eq. (7.37) for the function P
1
2
x:
7.11 Show that
d
nÿm
dx
nÿm
x
2
ÿ 1
n
n ÿ m!
n m!
x
2
ÿ 1
m
d
nm
dx
nm
x
2
ÿ 1
m
Hint: Write x
2
ÿ 1
n
x ÿ 1
n
x 1
n
and ®nd the derivatives by
Leibnitz's rule.
7.12 Use the generating function for the Hermite polynomials to ®nd:
(a) H
0
x; (b) H
1
x;(c) H
2
x;(d)H
3
x.
7.13 Verify that the generating function satis®es the identity
@
2
@x
2
ÿ 2x
@
@x
2t
@
@t
0:
Show that the functions H
n
x in Eq. (7.47) satisfy Eq. (7.38).
7.14 Given the diÿerential equation y
00
" ÿ x
2
y 0, ®nd the possible values
of " (eigenvalues) such that the solution yx of the given diÿerential equa-
tion tends to zero as x !1. For these values of ", ®nd the eigenfunctions
yx.
7.15 In Eq. (7.58), write the series for the exponential and co llect powers of z to
verify the ®rst few terms of the series. Verify the identity
x
@
2
@x
2
1 ÿ x
@
@x
z
@
@z
0:
Substituting the series (7.58) into this identity, show that the functions L
n
x
in Eq. (7.58) satisfy Laguerre's equation.
7.16 Show that
J
0
x1 ÿ
x
2
2
2
1!
2
x
4
2
4
2!
2
ÿ
x
6
2
6
3!
2
ÿ;
J
1
x
x
2
ÿ
x
3
2
3
1!2!
x
5
2
5
2!3!
ÿ
x
7
2
7
3!4!
ÿ:
7.17 Show that
J
1=2
x
2
x
1=2
sin x; J
ÿ1=2
x
2
x
1=2
cos x:
7.18 If n is a positive integer, show that the formal expression for J
ÿn
x gives
J
ÿn
xÿ1
n
J
n
x.
7.19 Find the general solution to the modi®ed Bessel's equation
x
2
y
00
xy
0
x
2
s
2
ÿ
2
y 0
which diÿers from Bessel's equation only in that sx takes the place of x.
344
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS
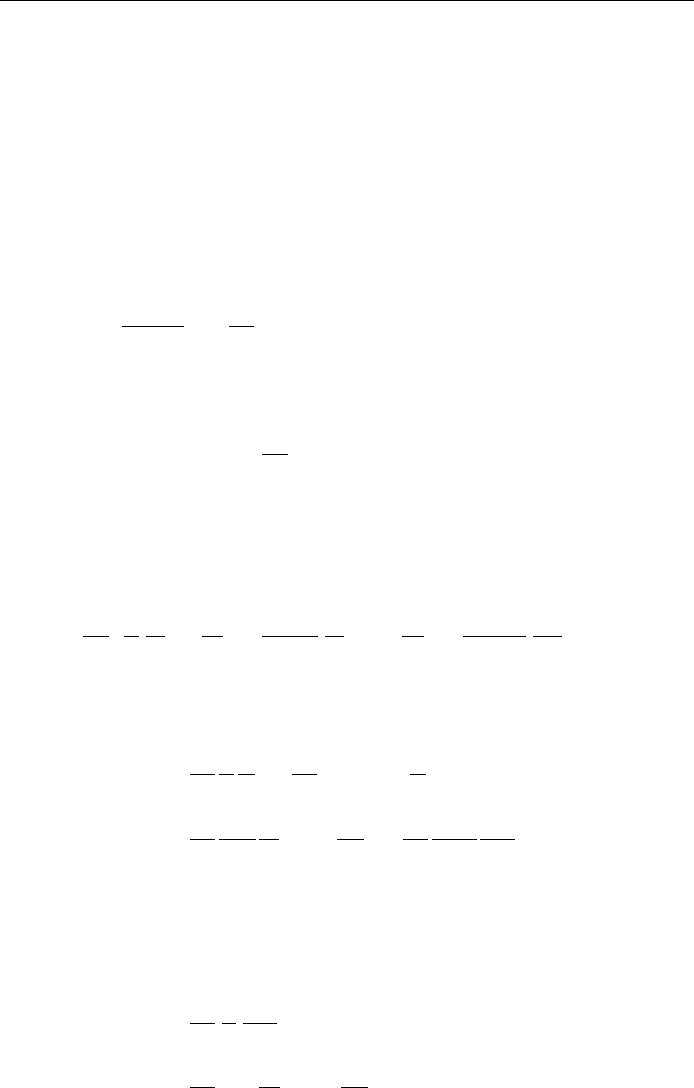
(Hint: Reduce the given equation to Bessel's equation ®rst.)
7.20 The lengthening simple pendulum: Consider a small mass m suspended by a
string of length l. If its length is increased at a steady rate r as it swings back
and forth freely in a vertical plane, ®nd the equation of motion and the
solution for small oscillations.
7.21 Evaluate the integrals:
a
Z
x
n
J
nÿ1
xdx; b
Z
x
ÿn
J
n1
xdx; c
Z
x
ÿ1
J
1
xdx:
7.22 In quantum mechanics, the three-dimensional Schro
È
dinger equation is
ip
@ýr; t
@t
ÿ
p
2
2m
r
2
ýr; tVýr; t; i
ÿ1
p
; p h=2:
(a) When the potential V is independ ent of time, we can write ýr; t
urTt. Show that in this case the Schro
È
dinger equation reduces to
ÿ
p
2
2m
r
2
urVurEur;
a time-independent equation along with Tte
ÿiEt=p
, where E is a
separation constant.
(b) Show that, in spherical coordinates, the time-independent Schro
È
dinger
equation takes the form
ÿ
p
2
2m
1
r
2
@
@r
r
2
@u
@r
1
r
2
sin
@
@
sin
@u
@
1
r
2
sin
2
@
2
u
@
"#
Vru Eu;
then use separation of variables, ur;;RrY; , to split it into
two equations, with as a new separation constant:
ÿ
p
2
2m
1
r
2
d
dr
r
2
dR
dr
V
r
2
R ER;
ÿ
p
2
2m
1
sin
@
@
sin
@Y
@
ÿ
p
2
2m
1
sin
2
@
2
Y
@
2
Y:
It is straightforward to see that the radial equation is in the form of Eq.
(7.99). Continuing the separation process by putting Y ; ,
the angular equation can be separated further into two equations, with
þ as separation constant:
ÿ
p
2
2m
1
d
2
d
2
þ;
ÿ
p
2
2m
sin
d
d
sin
d
d
ÿ sin
2
þ 0:
345
PROBLEMS
