Chow T.L. Mathematical Methods for Physicists: A Concise Introduction

Подождите немного. Документ загружается.

The action I may similarly be regarded as an explicit function of time, by

considering paths starting from a given point q

1 at a given instant t

, ending

at a given point q

2 at various times t

 t:

I  Iq

; t:

Then the total time derivative of I is









: 8:34

From the de®nition of the action, we have dI=dt  L. Substituting this into Eq.

(8.34), we obtain

 L ÿ

ÿH

 Hq

; p

; t0: 8:35

Replacing the momenta p

in the Hamiltonian H by @I=@q

as given by Eq. (8.33),

we obtain the Hamilton±Jacobi equation

Hq

;@I=@q

; t

 0: 8:36

For a conservative system with stationary constraints, the time is not contained

explicitly in Hamiltonian H,andH  E (the total energy of the system).

Consequently, according to Eq. (8.35), the dependence of action I on time t is

expressed by the term ÿEt. Therefore, the action breaks up into two terms, one of

which depends only on q

, and the other only on t:

Iq

; tI

q

ÿEt: 8:37

The function I

q

 is sometimes called the contracted action, and the Hamilton±

Jacobi equation (8.36) reduces to

Hq

;@I

=@q

E: 8:38

Example 8.8

To illustrate the method of Hamilton±Jacobi, let us consider the motion of an

electron of charge ÿe revolv ing about an atomic nucleus of charge Ze (Fig. 8.7).

As the mass M of the nucleus is much greater than the mass m of the electron, we

may consider the nucleus to remain stationary without making any very appreci-

able error. This is a cen tral force motion and so its motion lies entirely in one

plane (see Classical Mechanics, by Tai L. Chow, John Wiley, 1995). Employing

366

THE CALCULUS OF VARIATIONS

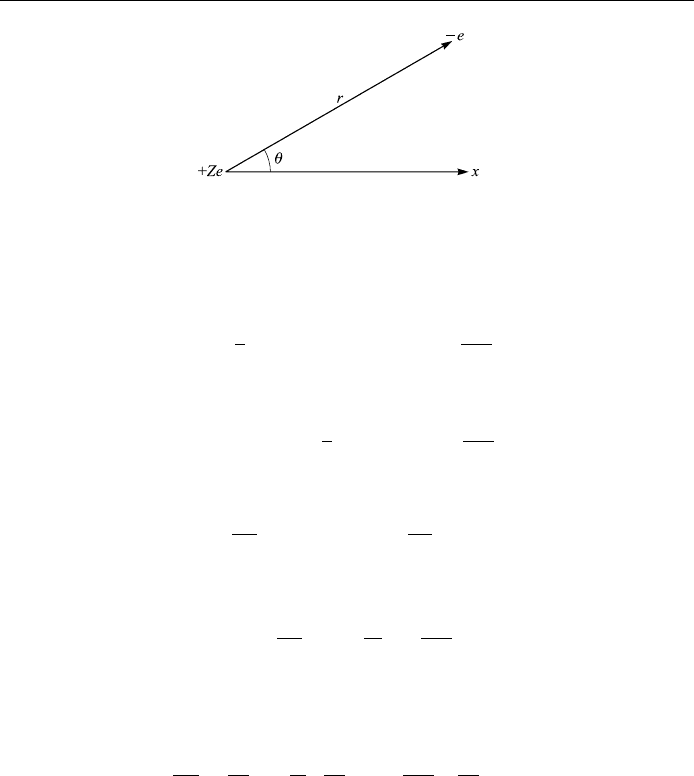
polar coordinates r and  in the plane of motion to specify the position of the

electron relative to the nucleus, the kinetic and potential energies are, respectively,

T 

m

 r



; V ÿ

Then

L  T ÿ V 

m

 r





and



 m







 mr

:

The Hamiltonian H is

H 





ü!

Replacing p

and p



in the Hamiltonian by @I=@r and @I=@, respectively, we

obtain, by Eq. (8.3 6), the Hamilton±Jacobi equation





@





 0:

Variational problems with several independent variables

The functional f in Eq. (8.1) contains only one independent variable, but very

often f may contain several independent variables. Let us now extend the theory

to this case of several independent variables:

I 

ZZZ

f fu; u

; u

; x; y; zdxdydz ; 8:39 

where V is assumed to be a bounded volume in space with prescribed values of

ux; y; z at its boundary S; u

 @u=@x, and so on. Now, the variational problem

367

VARIATIONAL PROBLEMS

Figure 8.7.

is to ®nd the function ux; y; z for which I is stationary with respect to small

changes in the functional form ux; y; z.

Generalizing Eq. (8.2), we now let

ux; y; z;"ux; y; z; 0"x; y; z; 8:40

where x; y; z is an arbitrary well-behaved (that is, diÿerentiable) function which

vanishes at the boundary S. Then we have, from Eq. (8.40),

x; y; z;"u

x; y; z; 0"

;

and similar expressions for u

; u

;and

"0



ZZZ

 













dxdydz  0:

We next integrate each of the terms @f =@u



using `integration by parts' and the

integrated terms vanish at the boundary as required. After some simpli®cations,

we ®nally obtain

ZZZ



x ; y; zdxdydz  0:

Again, since x; y; z is arbitrary, the term in the braces may be set equal to zero,

and we obtain the Euler±Lagrange equation:

 0: 8:41

Note that in Eq. (8.41) @=@x is a partial derivative, in that y and z are constant.

But @=@x is also a total derivative in that it acts on implicit x dependence and on

explicit x dependence:



@x@u



@u@u



: 8:42

Example 8.9

The Schro

dinger wave equation. The equations of motion of classical mechanics

are the Euler±Lagrange diÿerential equations of Hamilton's principle. Similarly,

the Schro

dinger equation, the basic equation of quantum mechanics, is also a

Euler±Lagrange diÿerential equation of a v ariational principle the form of which

is, in the case of a system of N particles, the following



Ld  0;  8 :43

368

THE CALCULUS OF VARIATIONS

with

L 

i1

@ÿ*

@ÿ



@ÿ*

@ÿ



@ÿ*

@ÿ



 Vÿ*ÿ 8:44

and the constraint

ÿ*ÿd  1 ; 8:45

where m

is the mass of particle I, V is the potential energy of the system, and d is

a volume element of the 3N-dimensional space.

Condition (8.45) can be taken into consideration by introducing a Lagrangian

multiplier ÿE:



L ÿ Eÿ*ÿd  0: 8:46

Performing the variation we obtain the Schro

dinger equation for a system of N

particles

i1

ÿ E ÿ Vÿ  0; 8:47

where r

is the Laplace operator relating to particle i. Can you see that E is the

energy parameter of the system? If we use the Hamiltonian operator

H, Eq. (8.47)

can be written as

Hÿ  Eÿ: 8:48

From this we obtain for E

E 

ÿ*Hÿd

ÿ*ÿd

: 8:49

Through partial integration we obtain

Ld 

ÿ*Hÿd

and thus the variational principle can be formulated in another way:



ÿ*H ÿ Eÿd  0.

Problems

8.1 As a simple practice of using varied paths and the extremum condition, we

consider the simple function yxx and the neighboring paths

369

PROBLEMS

y"; xx  " sin x. Draw these paths in the xy plane between the limits

x  0andx  2 for "  0 for two diÿerent non-vanishing values of ". If the

integral I" is given by

I"

2

dy=dx

dx;

show that the value of I" is always greater than I0, no matter what value

of " (positive or negative) is chosen. This is just condition (8.4).

8.2 (a) Show that the Euler±Lagrange equation can be written in the form

f ÿ y



 0:

This is often called the second form of the Euler±Lagrange equation.

(b)Iff does not involve x explicitly, show that the Euler±Lagrange equation

can be integrated to yield

f ÿ y

 c;

where c is an integration constant.

8.3 As shown in Fig. 8.8, a curve C joining points x

; y

 and x

; y

 is

revolved about the x-axis. Find the shape of the curve such that the surface

thus generated is a minimum.

8.4 A geodesic is a line that represents the shortest distance between two points.

Find the geodesic on the surface of a sphere.

8.5 Show that the geodesic on the surface of a right circular cylinder is a helix.

8.6 Find the shape of a heavy chain which minimizes the potential energy while

the length of the chain is constant.

8.7 A wedge of mass M and angle  slides freely on a horizontal plane. A

particle of mass m moves freely on the wedge. Dete rmine the motion of

the particle as well as that of the wedge (Fig. 8.9).

370

THE CALCULUS OF VARIATIONS

Figure 8.8.

8.8 Use the Rayleigh±Ritz method to analyze the forced oscillations of a har-

monic oscillation:



x  kx  F

sin !t:

8.9 A particle of mass m is attracted to a ®xed point O by an inverse square

force F

ÿk=r

(Fig. 8.10). Find the canonical equations of motion.

8.10 Set up the Hamilton±Jacobi equation for the simple harmonic oscillator.

371

PROBLEMS

Figure 8.9.

Figure 8.10.

The Laplace transformation

The Laplace transformation method is generally useful for obtaining solutions of

linear diÿ erential equations (both ordinary and partial). It enables us to reduce a

diÿerential equation to an algebraic equation, thus avoiding going to the trouble

of ®nding the general solution and then evaluating the arbitrary constants. This

procedure or technique can be extended to systems of equations and to integral

equations, and it often yields results more readily than other techniques. In this

chapter we shall ®rst de®ne the Laplace transformation, then evaluate the trans-

formation for some elementary functions, and ®nally apply it to solve some simple

physical problems.

De®nition of the Lap ace transform

The Laplac e transform Lf x of a function f x is de®ned by the integral

Lf x 

ÿpx

f xdx  Fp; 9:1

whenever this integral exists. The integral in Eq. (9.1) is a function of the para-

meter p and we denote it by Fp. The function Fp is called the Laplace trans-

form of f x. We may also look upon Eq. (9.1) as a de®nition of a Laplace

transform operator L which tranforms f x in to Fp. The operator L is linear,

since from Eq. (9.1) we have

Lc

f xc

gx 

ÿpx

f xc

gxgdx

 c

ÿpx

f xdx  c

ÿpx

gxdx

 c

Lf x  c

Lgx;

372

where c

and c

are arbitrary constants and gx is an arbitrary function de®ned

for x > 0.

The inverse Laplace transform of Fp is a function f x such that

Lf x  Fp. We denote the operati on of taking an inverse Laplace transform

by L

ÿ1

Fp   f x: 9:2

That is, we operate algebraically with the operators L and L

ÿ1

, bringing them

from one side of an equation to the other side just as we would in writing ax  b

implies x  a

ÿ1

b. To illustrate the calculation of a Laplace transform, let us

consider the following simple example.

Example 9.1

Find Le

, where a is a constant.

Solution: The transform is

Le



ÿpx

dx 

ÿpÿax

dx:

For p  a, the exponent on e is positive or zero and the integral diverges. For

p > a, the integral converges:

Le



ÿpx

dx 

ÿpÿax

dx 

ÿpÿax

ÿp ÿ a



p ÿ a

This example enables us to investigate the existence of Eq. (9.1) for a general

function f x.

Existence of Laplace transforms

We can prove that:

(1) if f x is piecewise continuous on every ®nite interval 0  x  X, and

(2) if we can ®nd constants M and a such that jf xj  Me

for x  X,

then Lf x exists for p > a. A function f x which satis®es condition (2) is said

to be of exponential order as x !1; this is mathematician's jargon!

These are sucient conditions on f x under which we can guarantee the

existence of Lf x. Under these conditions the integral converges for p > a:

f xe

ÿpx



f x

ÿpx

dx 

ÿpx

 M

ÿpÿax

dx 

p ÿ a

373

EXISTENCE OF LAPLACE TRANSFORMS

This establishes not only the convergence but the absolute convergence of the

integral de®ning Lf x. Note that M=p ÿ a tends to zero as p !1. This

shows that

lim

p!1

Fp0 9 :3

for all functions FpLf x such that f x satis®es the foregoi ng conditions

(1) and (2). It follows that if lim

p!1

Fp60, Fp cannot be the Laplace trans-

form of any function f x.

It is obvious that functions of exponential order play a dominant role in the use

of Laplace transforms. One simple way of determining whether or not a speci®ed

function is of exponential order is the following one: if a constant b exists such

that

lim

x!1

ÿbx

f x

9:4

exists, the function f x is of exponential order (of the order of e

ÿbx

. To see this,

let the value of the above limit be K 6 0. Then, when x is large enough, je

ÿbx

f xj

can be made as close to K as possible, so certainly

ÿbx

f xj < 2K:

Thus, for suciently large x,

jf xj < 2Ke

jf xj < Me

; with M  2K:

On the other hand, if

lim

x!1

e

ÿcx

f x

jj

1 9:5

for every ®xed c, the function f x is not of exponential order. To see this , let us

assume that b exists such that

jf xj < Me

for x  X

from which it follows that

ÿ2bx

f xj < Me

ÿbx

Then the choice of c  2b would give us je

ÿcx

f xj < Me

ÿbx

, and e

ÿcx

f x!0as

x !1which contradicts Eq. (9.5).

Example 9.2

Show that x

is of exponential order as x !1.

374

THE LAPLACE TRANSFORMATION

Solution: We have to check whether or not

lim

x!1

ÿbx



 lim

x!1

exists. Now if b > 0, then L'Hospital's rule gives

lim

x!1

ÿbx



 lim

x!1

 lim

x!1

 lim

x!1

 lim

x!1

 0:

Therefore x

is of exponential order as x !1.

Laplace transforms of some elementary functions

Using the de®nition (9.1) we now obtain the transform s of polynomials, expo-

nential and trigonometric functions.

(1) f x1 for x > 0.

By de®nition, we have

L1

ÿpx

dx 

; p > 0:

(2) f xx

, where n is a positive integer.

By de®nition, we have

Lx



ÿpx

dx:

Using integration by parts:

dx  uv ÿ

with

u  x

; dv  v

dx  e

ÿpx

dx ÿ1=pde

ÿpx

; v ÿ1=pe

ÿpx

;

we obtain

ÿpx

dx 

ÿx

ÿpx





ÿpx

nÿ1

dx:

For p > 0 and n > 0, the ®rst term on the right hand side of the above equation is

zero, and so we have

ÿpx

dx 

ÿpx

nÿ1

375

LAPLACE TRANSFORMS OF ELEMENTARY FUNCTIONS