Choudhry. Fixed Income Securities Derivatives Handbook

Подождите немного. Документ загружается.

322 Selected Market Trading Considerations

Treasury announced it was discontinuing. With the return to large budget

deﬁ cits during the Bush administration, however, issuance has resumed,

and the impact of low supply has abated.

Liquidity differences often produce yield differences among bonds

with similar durations. Institutional investors prefer to hold the bench-

mark bond—the current 2-, 5-, 10-, or 30-year issue—which both

increases its liquidity and depresses its yield. The converse is also true:

because more-liquid bonds are easier to convert into cash if necessary,

demand is higher for them, and their yields are thus lower. The effect

of liquidity on yield can be observed by comparing the market price of

a six-month bond with its theoretical value, derived by discounting its

cash ﬂ ow at the current 6-month T-bill rate. The market price—which

is equal to the present value of its cash ﬂ ow discounted at its yield—

is lower than the theoretical value, reﬂ ecting the fact that the T-bill yield

is lower than the bond yield, even though the two securities’ cash ﬂ ows

fall on the same day. The reason is liquidity: the T-bill is more readily

realizable into cash at any time.

A bond’s coupon and liquidity, as well as its duration, thus help

determine the yield at which it trades. Accordingly, analyses of relative

value among bonds consider these factors in conjunction with others.

FIGURE 17.4 Yields of Bonds with Similar Durations but

Different Coupons, Given an Inverted Curve

Duration (years)

Spread (bps)

High-coupon bonds

Low-coupon bonds

–4

–3

–2

–1

0.5

12 433571015

–5

Approaches to Trading 323

Characterizing the Complete Term Structure

As many readers undoubtedly have gathered, the traditional yield curve

illustrated in Figure 17.4 is inadequate for analyzing the market. This is

because it highlights only the curve’s general shape, which is not a suf-

ﬁ cient basis on which to make trading decisions. This section describes a

technique for gaining a more complete, and useful, picture.

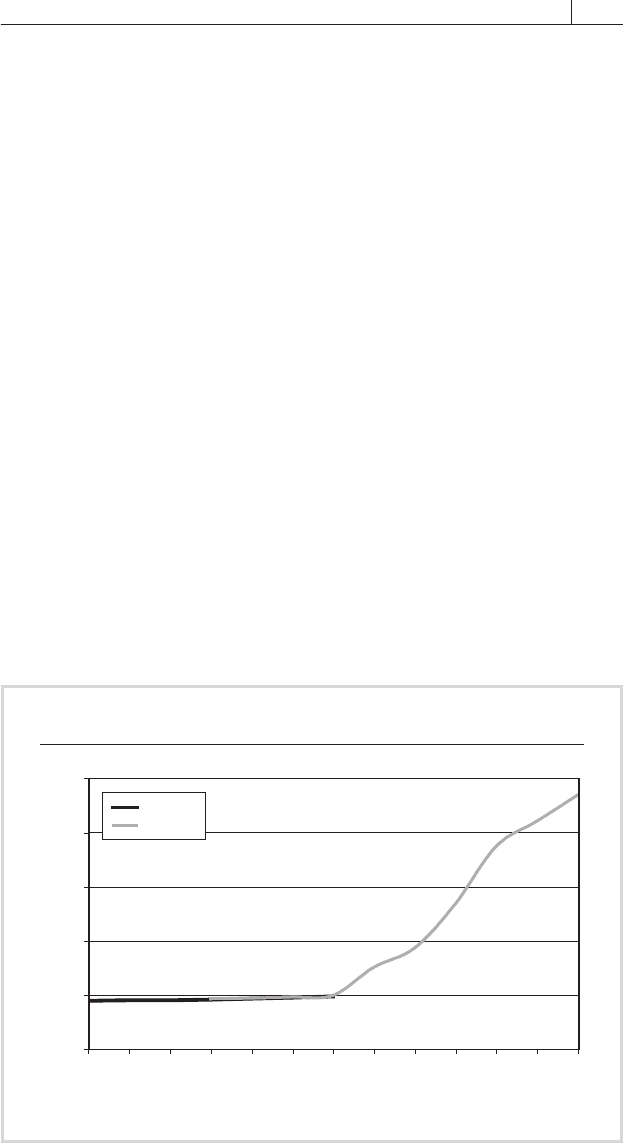
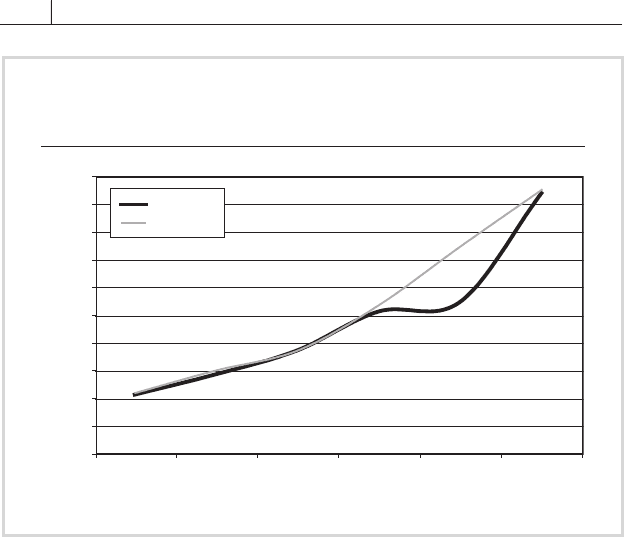
FIGURE 17.5 graphs the March 2004 bond par yield curve against the

T-bill yield curve for the same date. The two curves in

FIGURE 17.6 repre-

sent the low-coupon and high-coupon yield spreads—that is, the yield dif-

ferences between coupon bonds trading at par and, in the ﬁ rst case, bonds

with coupons 100 basis points below the par yield and, in the second case,

those with coupons 100 basis points above the par yield. By watching and

comparing the curves illustrated in the two ﬁ gures, investors can see the

impact of coupons on the shape of the par yield curve and on yields at

different maturity points.

Identifying Relative Value in Government Bonds

This section discusses the factors that must be assessed in analyzing the rel-

ative values of government bonds. Since these securities involve no credit

risk (unless they are emerging-market debt), credit spreads are not among

the considerations. The zero-coupon yield curve provides the framework

for all the analyses explored.

FIGURE 17.5 T-Bill and Par Yield Curves, March 2004

Term to maturity

Yield (%)

T-Bill

Treasuries

30 day 45 day 60 day 90 day 4M 5M 6M 2Y 3Y 5Y 10Y 20Y 30Y

Treasury curve includes interpolated yields.

Source: Bloomberg

324 Selected Market Trading Considerations

The objective of much bond analysis is to determine the relative values

of individual securities and thus identify which should be purchased and

which sold. Such decisions are, at the broadest level, a function of whether

one thinks interest rates are going to rise or fall. Analysis in this sense

identiﬁ es securities’ absolute value. More locally based analysis focuses on

speciﬁ c sectors of the yield curve and is aimed at determining whether

these will ﬂ atten or steepen, or whether bonds with similar durations are

trading at large enough spreads to warrant switching from one to another.

This type of analysis identiﬁ es relative value.

On rare occasions, assessing relative value is fairly straightforward. If the 3-

year yield were 5.75 percent, the 2-year 5.70 percent, and 4-year 6.15 percent,

for example, 3-year bonds would appear to be overpriced. Such situations,

however, do not occur often in real life. More realistically, the 3-year bond’s

value would have to be assessed relative to much shorter- or longer-dated in-

struments. Comparing a short-dated bond with other short-term securities is

considerably different from comparing, say, the 2-year bond to the 30-year.

Although, in a graph, the smooth curve linking 1-year to 5-year yields appears

to be repeated from the 5-year out to the 30-year, in reality the very short-

dated sector of the yield curve often behaves independently of the long end.

One method of identifying relative value is to quantify the effect

of coupon rates on bond yields. The relationship between the two is

expressed in equation (17.2).

FIGURE 17.6 Par and High- and Low-Coupon Yield Curves,

March 2004

Term to maturity (years)

Yield (%)

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

4.5

5.0

12351030

High coupon

Low coupon

Source: Bloomberg

Approaches to Trading 325

rm rm c C rm d C rm

PPDP PDP

=+× −

()

+× −

()

max , min ,00

(17.2)

where

rm = the yield of the bond being analyzed

= the yield of a par bond of speciﬁ ed duration

= the coupon of an arbitrary bond whose duration is similar to the

par bond’s

c = a coefﬁ cient representing the effect of a high coupon on a bond’s

yield

d = a coefﬁ cient representing the effect of a low coupon on a bond’s

yield

When the par bond yield is lower than the coupon of the bond having

a similar duration—that is, C

> rm

, (17.2) reduces to (17.3).

rm rm c C rm

PPDP

=+×−

()

(17.3)

Equation 17.3 expresses the yield spread between a high-coupon bond

and a par bond as a linear function of the spread between the ﬁ rst bond’s

coupon and the par bond’s yield and coupon. In reality, this relationship

may not be purely linear. The yield spread between the two bonds, for

instance, may widen more slowly when the gap between the coupons is

very large. Equation 17.3 thus approximates the effect of a high coupon

on yield more accurately for bonds trading close to par.

The same analysis can be applied to bonds with coupons lower than

the coupon of the par bond having the same duration.

A bond may be valued relative to comparable securities or against the

par or zero-coupon yield curve. The ﬁ rst method is more appropriate in

certain situations. It is suitable, for instance, when a low-coupon bond is

trading rich to the curve but fair compared with other low-coupon bonds.

This may indicate that the overpricing is a property not of the individual

bond but of all low-coupon bonds.

The comparative value analysis can be extended from the local struc-

ture of the yield curve to groups of similar bonds. This is an important

part of the analysis, because it is particularly informative to know the

cheapness or costliness of a single issue relative to the whole yield curve.

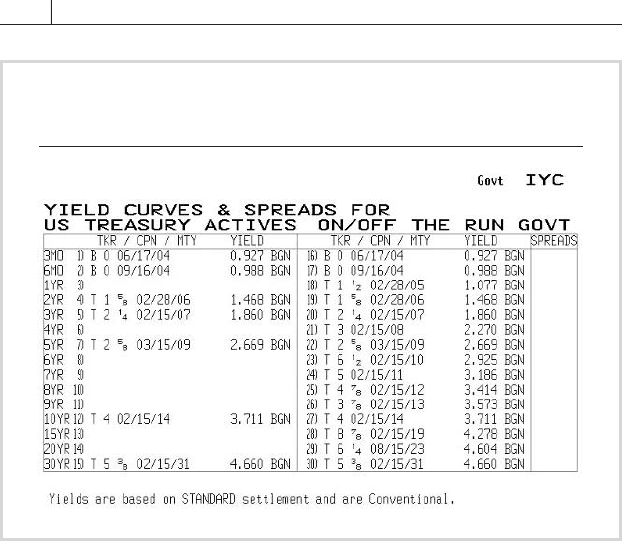
Traders may use the technique described above to identify excess positive

or negative yield spreads for all the bonds in the term structure, resulting in

a list like that in

FIGURE 17.7. From these, they might select two or more

bonds, some of which are cheap and others expensive relative to the curve,

then switch between them or put on a spread trade.

326 Selected Market Trading Considerations

The benchmark securities in the ﬁ gure are all expensive relative to

the par curve, and the less-liquid bonds are cheap. The 2

/8 percent 2009

appears cheap, but the 6

/2 percent 2010, which has a shorter duration,

offers a higher yield. This curious anomaly disappeared a few days later, so,

if not taken advantage of immediately, the proﬁ t opportunity was lost.

Hedging Bond Positions

A hedge is a position in a cash or off-balance-sheet instrument that removes

the market risk exposure of another position. For example, a long position

in 10-year bonds can be hedged with a short position in 20-year issues or

with futures contracts. The concept is straightforward. Implementing it

effectively, however, requires a precise calculation of the amount of the

hedge needed, and that can be complex.

Simple Hedging Approaches

Say an investor wishes to hedge a position in one of the bonds listed in

ﬁ gure 17.7 with a counterbalancing position in another of these issues. As

explained in chapter 2, it is possible to calculate the size of the position

required for a duration-weighted hedge using the ratio of the two bonds’

basis point values, or BPVs—that is, the change in their prices correspond-

ing to a 1–basis point change in yields. This approach is very common in

FIGURE 17.7 Yields and Excess Yield Spreads for Five Treasuries

and Less-Liquid Issues, March 24, 2004

Source: Bloomberg

Approaches to Trading 327

the market. It is based, however, on two assumptions that hinder its ef-

fectiveness: ﬁ rst, that the two bonds’ yields have comparable volatility and,

second, that changes in the yields of the two bonds are highly correlated.

This implies that the changes in yields are highly positively correlated.

Correlation refers to changes in direction, not absolute values. Highly cor-

related means that if Bond A increases from 10 to 12, and Bond B is at

79.25, its price will increase too. In situations where one or both of these

assumptions fails to hold, the hedge is compromised.

The assumption of comparable yield volatility becomes increasingly

unrealistic the more the bonds differ in terms of market risk and behavior.

Say the position to be hedged is a $1 million holding of the 5-year issue

in ﬁ gure 17.7 and the hedging instrument is the 5-year bond. A duration-

weighted hedge would consist of a short position in the 5-year. Even if the

two bonds’ yields are perfectly correlated, they might still change by differ-

ent amounts if the bonds have different yield volatilities. Say the 2-year is

twice as volatile as the 5-year. That means the 5-year yield moves only half

as far as the 2-year in the same situation. For instance, an event causing

the latter to rise 5 basis points would effect a mere 2.5-basis-point increase

in the former. So a hedge calculated according to the two bonds’ BPV and

assuming an equal change in yield for both bonds would be incorrect.

Speciﬁ cally, the short position in the 5-year bond would effectively hedge

only half the risk exposure of the 2-year position.

The assumption of perfectly correlated yield changes is similarly un-

realistic and so causes similar misweightings. Although bond yields across

the whole term structure are positively correlated most of the time, this is

not always the case. Returning to the example, assume that the 2-year and

5-year bonds possess identical yield volatilities but that changes in their

yields are uncorrelated. This means that a 1-basis-point fall or rise in the

2-year yield implies nothing about change in the 5-year yield. That, in

turn, means that the 5-year bonds cannot be used to hedge 2-year bonds,

at least not with any certainty.

Hedge Analysis

From the preceding discussion, it is clear that at least two factors beyond

BPV determine the effectiveness of a bond hedge: the bonds’ yield volatili-

ties and the extent to which changes in their yields are correlated.

FIGURE 17.8 shows the standard deviations—that is, volatilities—and

correlations of weekly yield changes for a set of Treasuries during the nine

months to March 2004. Note that, contrary to the assumptions inher-

ent in the BPV hedge calculation, volatilities are far from uniform, and

yield changes are imperfectly correlated. The standard deviation of weekly

yield changes is highest for the short-dated paper and declines throughout

328 Selected Market Trading Considerations

the period for longer-dated paper. Correlations, as might be expected,

are highest among bonds in the same maturity sectors and decline as

they move farther apart along the yield curve; for example, two-year

bond yields are more positively correlated with ﬁ ve-year yields than with

30-year ones.

Hedges can be made more accurate by adjusting their weightings

according to the standard relationship for correlations and the effect of

correlation. Consider two bonds with nominal values M

and M

. If the

bonds’ yields change by

∆r

and ∆r

, the net change in the position’s

value is given by equation (17.4)

∆∆∆PV M BPV r M BPV r=+

111 222

(17.4)

The change in net value of a two-bond position is a function of the two

securities’ nominal values, their volatilities, and the correlation between

their yield changes. The standard deviation of such a position may there-

fore be expressed by equation (17.5).

σσσ σσρ

pos

M BPV M BPV M M BPV BPV=++

12 1 212

2 (17.5)

FIGURE 17.8 Yield Volatilities and Correlations, Selected Bonds,

Nine Months to March 2004

SEGMENT

2-YEAR 3-YEAR 5-YEAR 10-YEAR 20-YEAR 30-YEAR

VOLATILITY (BP) 18.7 19.5 20.2 20.0 20.6 21.2

CORRELATION

2-year 1.000 0.973 0.949 0.919 0.887 0.879

3-year 0.973 1.000 0.961 0.935 0.901 0.889

5-year 0.949 0.961 1.000 0.968 0.951 0.945

10-year 0.919 0.935 0.968 1.000 0.981 0.983

20-year 0.887 0.901 0.951 0.981 1.000 0.987

30-year 0.879 0.889 0.945 0.983 0.987 1.000

Approaches to Trading 329

where

= the correlation between the yield volatilities of bonds 1 and 2

Equation (17.5) can be rearranged as shown in (17.6) to solve for the

optimum hedge value for any bond.

BPV

=−

ρσ

(17.6)

where

= the nominal value of the bond used to hedge nominal value M

of the ﬁ rst bond

The lower the correlation between the two bonds’ yields—and, thus,

the more independent changes in one are of changes in the other—

the smaller the optimal hedge position. If the two bonds’ yields exhibit

identical volatility and change in lockstep—a correlation of 1—equation

(17.6) reduces to equation (17.7), the traditional hedge calculation, based

solely on BPV.

BPV

(17.7)

Summary of the Derivation

of the Optimum-Hedge Equation

According to equation (17.5), the variance of a net change in the value of

a two-bond portfolio is given by equation (17.8), which can be rewritten

as (17.9), using the partial derivative of the variance σ

with respect to the

nominal value of the second bond.

σσσ σσρ

pos

M BPV M BPV M M BPV BPV

12 1 212

2=++ (17.8)

∂

σσσρ

11212

M BPV M BPV BPV (17.9)

Setting equation (17.5) to zero and solving for M

gives equation

(17.10), which is the hedge quantity for the second bond.

BPV

=−

ρσ

(17.10)

This page is intentionally blank

331

The Black-Scholes Model

in Microsoft Excel

APPENDIX

he ﬁ gure on the following page shows the spreadsheet formulas

required to build the Black-Scholes model in Microsoft Excel.

The Analysis Tool-Pak add-in must be available, otherwise some

of the function references may not work. Setting up the cells in the way

shown enables the fair value of a vanilla call or put option to be calcu-

lated. The latter calculation employs the put-call parity theorem.

Price of underlying 100

Volatility 0.0691

Option maturity 3 months

Strike price 99.5

Risk-free rate 5%