Чернов В.П. Операционный и производственный менеджмент

Подождите немного. Документ загружается.

123

Q – размер партии;

X – максимальный объем запаса на складе;

L – средние издержки в единицу времени без учета стоимости партии;

L – средние издержки в единицу времени с учетом стоимости партии.

Связи между характеристиками модели

T = Q/α, Q = αT, X = (β - α)T′,

′ = X/(β - α), X = αT′′, T′′ = X/α,

T = T

′ + T′′ = X/(β - α) + X/α = X/(α/(1 - α/β)),

Q =

αT = X + αT′ = X/(1 - α/β), X = Q(1 - α/β), X = Tα(1 - α/β),

L = (a + bXT/2)/T = (a + b

α(1 - α/β)T

/2)/T = a/T + bα(1 - α/β)T/2 = aα/Q

+ b(1 -

α/β)Q/2,

L = L + cα.

Характеристики оптимальной стратегии

Оптимальная стратегия определяется теми значениями характеристик

T* , T

′* , T′′* , Q* , X* , L* иL* , при которых издержки L становятся

минимальными. Достаточно найти одну из этих характеристик, остальные

определятся через нее однозначно на основе приведенных выше соотноше-

ний.

Оптимизационные формулы

T* = (2a/(αb(1 - α/β)))

0,5

T′* = (2aα/(β

b(1 - α/β)))

0,5

, T′′* = (2a (1 - α/β)/αb)

0,5

Q* = (2a

α/(b(1 - α/β)))

0,5

, X* = (2aα(1 - α/β)/b)

0,5

L* = (2a

αb(1 - α/β))

0,5

, L* = L* + cα = (2aαb(1 - α/β))

0,5

+ cα.

В оптимизационных формулах присутствует величина:

1 - α/β.

124

Отношение α/β сопоставляет интенсивность спроса с интенсивно-

стью поставки. Рост интенсивности поставки в пределе приводит к ситуа-

ции мгновенной поставки. Оптимизационные формулы для нашей модели

в пределе, при

α/β → 0, переходят в формулы для рассмотренной выше

простейшей модели с мгновенной поставкой. При этом, в частности, ста-

новится:

Q* = X*, T′′* = T, T′* = 0.

МОДЕЛЬ УПРАВЛЕНИЯ ЗАПАСАМИ С ДОПУЩЕНИЕМ

ДЕФИЦИТА

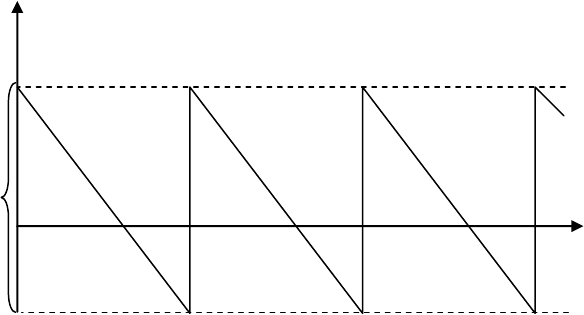
Рассмотрим детерминированную модель с мгновенной поставкой,

постоянной интенсивностью спроса и допущением дефицита – допущени-

ем отложенного спроса. График динамики запасов изображен на рис. 4.5.

Q T

0 T 2T 3T t

Рис. 4.5. Динамика складского запаса в модели с допущением дефицита

В течение промежутка времени T

спрос на продукцию удовлетво-

ряется за счет имеющегося запаса. Далее в течение промежутка T

запас

отсутствует, возникает ситуация дефицита, постепенно накапливается

долг величины S по неудовлетворенному спросу. Этот долг удовлетворя-

ется за счет части поступившей партии Q, после чего на складе остается

запас X, и все возобновляется по циклу. Длина цикла T = T

+ T

Штраф за дефицит исчисляется на основе коэффициента g – издер-

жек за единицу объема дефицита в единицу времени.

125

Параметры модели с мгновенной поставкой и допущением

дефицита

α – объем спроса в единицу времени (интенсивность спроса);

a – фиксированные издержки, связанные с актом пополнения запаса;

b – издержки по хранению единицы запаса в течение единицы времени;

g – величина издержек за единицу дефицита в течение единицы времени.

Характеристики модели

T – длина цикла управления запасами;

– интервал удовлетворения спроса (интервал наличия запаса и отсутст-

вия дефицита);

– интервал учета спроса (интервал отсутствия запаса и наличия дефицита);

Q – размер партии;

X – максимальный объем запаса на складе;

S – максимальный объем дефицита;

L – средние издержки в единицу времени без учета стоимости партии;

L – средние издержки в единицу времени с учетом стоимости партии.

Связи между характеристиками модели

T = T

+ T

, Q = X + S, Q = αT,

T = Q/α, T

= X/α, T

= S/α,

X = αT

, S = αT

L = (a + bXT

/2 + gST

/2)/T = (a + bαT

/2 + gαT

/2)/(T

+ T

L = L + cα.

Характеристики оптимальной стратегии

Оптимальная стратегия определяется теми значениями характеристик

T* , T

* , T

* , Q* , X* , S*, при которых издержки L становятся мини-

мальными. Достаточно найти дополняющую пару этих характеристик, на-

пример, T

* и T

* или, например, X* и S*, остальные определятся через

них однозначно на основе приведенных выше соотношений.

126

Оптимизационные формулы

T* = (2a(1 + b/g)/(αb))

0,5

* = (2a/(αb(1 + b/g)))

0,5

, T

* = (2ab/(αg

(1 + b/g)))

0,5

Q* = (2aα(1 + b/g)/b)

0,5

X* = (2aα/(b(1 + b/g)))

0,5

, S* = (2aαb/(g

(1 + b/g)))

0,5

bX* = gS*,

L* = (2aαb/(1 + b/g))

0,5

, L* = L* + cα = (2aαb/(1 + b/g))

0,5

+ cα.

В оптимизационных формулах присутствует величина 1 + b/g. Обратная

ей величина, 1 / (1 + b/g)), называется

плотностью убытков из-за дефицита.

Отношение b/g сопоставляет затраты по хранению и по дефициту.

Рост штрафа за дефицит в пределе приводит к запрету дефицита ввиду его

абсолютной невыгодности. Оптимизационные формулы для нашей моде-

ли в пределе, при b/g

→ 0, переходят в формулы для рассмотренной выше

простейшей модели без дефицита. При этом, в частности, становится:

Q* = X*, S* = 0, T

* = T, T

* = 0.

МОДЕЛЬ УПРАВЛЕНИЯ ЗАПАСАМИ С РАСТЯНУТОЙ

ПОСТАВКОЙ И ДОПУЩЕНИЕМ ДЕФИЦИТА

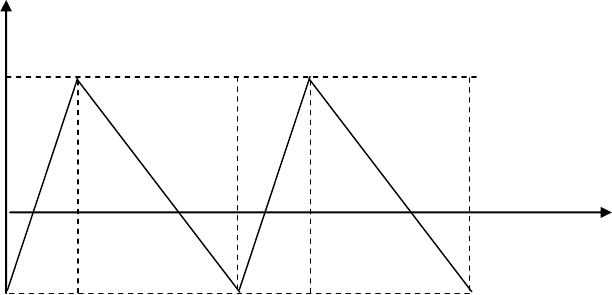
Рассмотрим теперь наиболее общую из детерминированных моде-

лей – модель с растянутой поставкой, постоянной интенсивностью спроса

и допущением дефицита. График динамики запаса изображен на рис. 4.6.

′ T

′′ T

′ T

′′

′ T

′′ T T

′ T

′′ 2T t

Рис. 4.6. Динамика запаса в модели с растянутой поставкой и допущением

дефицита

127

Цикл управления T разделяется на 4 части:

T = T

′ + T

′′ + T

′ + T

′′.

В течение T′ = T

′ + T

′ происходит одновременное пополнение и

расход запаса, в течение T

′′ = T

′′ + T

′′ идет чистый расход запаса.

Часть T

= T

′ + T

′′ соответствует наличию запаса, часть T

= T

′ +

′′ наличию дефицита.

Параметры модели с растянутой поставкой и допущением

дефицита

α – объем спроса в единицу времени (интенсивность спроса);

a – фиксированные издержки, связанные с актом пополнения запаса;

b – издержки по хранению единицы запаса в течение единицы времени;

g – величина издержек за единицу дефицита в течение единицы времени;

β – объем поставки в единицу времени (интенсивность поставки).

Характеристики модели

T – длина цикла управления запасами;

′ – интервал удовлетворения спроса (интервал наличия запаса и отсутст-

вия дефицита) в условиях осуществления поставки;

′′ – интервал удовлетворения спроса (интервал наличия запаса и отсут-

ствия дефицита) в условиях отсутствия поставки;

′ – интервал учета спроса (наличия дефицита и отсутствия запаса) в ус-

ловиях осуществления поставки;

′′ – интервал учета спроса (наличия дефицита и отсутствия запаса) в ус-

ловиях отсутствия поставки;

Q – размер партии;

X – максимальный объем запаса на складе;

S – максимальный объем дефицита;

L – средние издержки в единицу времени без учета стоимости партии;

L – средние издержки в единицу времени с учетом стоимости партии.

128

Связи между характеристиками модели

T = T

′ + T

′′ + T

′ + T

′′, Q = αT, T = Q/α,

X = αT

′′ = (β - α) T

′, T

′ = X/(β - α), T

′′ = X/α,

S = αT

′′ = (β - α) T

′, T

′ = S/(β - α), T

′′ = S/α,

T = (X + S)/(α(1 - α/β)), Q = X + S + α(T

′ + T

′ ), Q = β(T

′ + T

′ ),

L = (a + bX(T

′ + T

′′ )/2 + gS(T

′ + T

′′ )/2)/T =

= (a + (bX

/(α(1 - α/β)))/2 + (gS

/(α(1 - α/β)))/2)/((X + S)/(α(1 - α/β))),

L = L + cα.

Характеристики оптимальной стратегии

Оптимальная стратегия определяется теми значениями характери-

стик T* , T

′* , T

′′* , T

′* , T

′′* , Q* , X* , S* , при которых издержки

L становятся минимальными. Достаточно найти согласованную допол-

няющую пару этих характеристик, например, X* и S*, остальные опреде-

лятся через них однозначно на основе приведенных выше соотношений.

Оптимизационные формулы

T* = (2a(1 + b/g)/(αb(1 - α/β)))

0,5

′* = (2aα/(bβ(1 - α/β)(1 + b/g)))

0,5

′′* = (2a(1 - α/β)/(αb(1 + b/g)))

0,5

′* = (2aαb/(βg

(1 - α/β)(1 + b/g)))

0,5

′′* = (2ab(1 - α/β)/(αg

(1 + b/g)))

0,5

Q* = (2aα(1 + b/g)/(b(1 - α/β)))

0,5

X* = (2aα(1 - α/β)/(b(1 + b/g)))

0,5

S* = (2aαb(1 - α/β)/(g

(1 + b/g)))

0,5

bX* = gS*,

L* = (2aαb(1 - α/β)/(1 + b/g))

0,5

L* = L* + cα = (2aαb(1 - α/β)/(1 + b/g))

0,5

+ cα.

129

В оптимизационных формулах присутствуют величины 1 + b/g и

1 -

α/β. Рост штрафа за дефицит приводит в пределе к модели без дефицита,

а рост интенсивности поставки приводит к модели с мгновенной поставкой.

Оптимизационные формулы для нашей модели в пределе, при

b/g → 0 или при α/β → 0, переходят в формулы для рассмотренных выше

моделей.

МНОГОПРОДУКТОВЫЕ ЗАПАСЫ

На складе хранятся запасы продукции различных видов. Если они

не взаимодействуют (не конкурируют) между собой, то запасы каждого

вида можно оптимизировать отдельно, независимо от других.

Однако обычно между запасами возникает взаимодействие. Напри-

мер, хранение продукции одного вида может требовать таких условий ос-

вещенности, влажности, температуры, которые не согласуются с условия-

ми хранения других видов продукции. Продукты конкурируют за режим

хранения. Суммарная стоимость оптимальных партий может не вписы-

ваться в бюджет организации. Возникает конкуренция за ограниченный

объем затрат. Одновременно поступившие оптимальные партии разных

продуктов могут не помещаться на площади склада. Возникает конкурен-

ция за использование ограниченной площади. Совместно вывозимые пар-

тии разных продуктов могут не помещаться в одном контейнере. Возника-

ет конкуренция за объем контейнера.

В такого рода ситуациях индивидуальная оптимизация по каждому

виду продукции отдельно не дает эффекта, требуется совместная оптими-

зация. Решается задача поиска условного экстремума, в общем случае на

основе функции Лагранжа.

Модель с совмещением поставок

Предположим, что поставки на склад n товаров осуществляются из

одной географической точки, и поэтому они могут быть совмещены. Про-

анализируем возможность уменьшения затрат путем совмещения постав-

ки и экономии на транспортировке.

Пусть, как обычно,

a – постоянные затраты (одни и те же по любому виду товара);

– коэффициент переменных затрат по i-му товару;

– интенсивность спроса по i-му товару.

130

Мы будем исходить из того, что стратегия управления запасами яв-

ляется регулярной. Если поставки осуществляются совместно по всем n

продуктам, то периодичность поставок оказывается единой.

Обозначим соответствующий период (цикл управления запасами)

посредством T. Тогда размер партии i-го товара Q

определяется формулой:

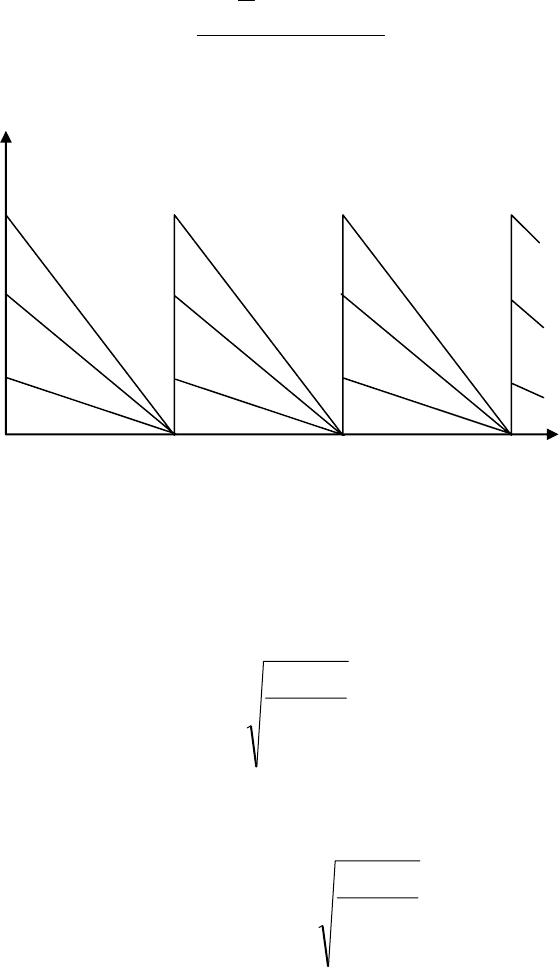
При таких объемах поставки запасы всех продуктов исчерпываются

одновременно, в конце периода T, в этот момент поступает новая партия,

и цикл возобновляется (рис. 4.7).

Затраты в единицу времени определяются формулой:

∑

α⋅+

0 T 2T 3T t

Рис. 4.7. Динамика трех видов запасов при согласованном цикле

Минимум затрат, определяемый так же, как и в выводе формул

Уилсона, достигается при величине цикла:

∑

и при этом размер партии k-го товара равен:

∑

⋅α=α=

131

а минимальные затраты по управлению запасами в единицу времени равны:

∑

α=

ba2L .

Если есть возможность совместить транспортировку различных то-

варов, то это следует сделать. Грузоподъемность транспортного средства

предполагается ограниченной некоторой величиной P. Рассчитанные оп-

тимальные размеры партии товаров, подготовленные к совместной транс-

портировке, могут превысить допустимую грузоподъемность P.

Для корректировки партии следует сравнить сумму оптимальных

величин

с грузоподъемностью. Обозначим посредством R сумму оп-

тимальных размеров партий:

∑

Если при этом P

≤ , то размер партии товаров следует сохранить

равным найденным выше значениям

Q. Если же это неравенство не вы-

полнено, то есть если

> , то значения

Q следует откорректировать до

новых величин

Эти новые величины должны по-прежнему соответствовать усло-

виям единого цикла управления запасами. Таким образом, необходимо от-

корректировать длину цикла. Обозначим новую длину посредством

Тогда:

α= ,

и при этом

∑

Отсюда получаем формулу для откорректированной длины цикла

∑

Новые, откорректированные размеры партии определяются по

формулам:

∑

⋅α=

Они полностью вписываются в грузоподъемность P:

132

∑

⋅α=

и соответствуют единому циклу управления запасами

Отметим, что новые размеры партий

и новая длина единого

цикла

пропорциональны прежним оптимальным величинам

Q и

T с

одним и тем же коэффициентом пропорциональности h, равным:

h =

Действительно, при P = R сумма оптимальных партий в точности

вмещается в транспортное средство, так что при этом условии мы должны

получить:

∑

Таким образом,

⋅=

∑

Аналогично,

QhThThT

⋅=⋅α⋅=⋅⋅α=α=

Новые размеры партии и длина цикла пропорциональны прежним

оптимальным величинам. Новые издержки

по управлению запасами в

единицу времени тоже пропорциональны прежним оптимальным издерж-

кам

L, но с другим коэффициентом пропорциональности H:

LHL

⋅

где

)

H += .

Минимальное значение этого коэффициента H равно 1. Оно дости-

гается только при h = 1, то есть при условии R = P. В этом случае откор-

ректированные величины длины цикла, размера партии и минимальных

издержек совпадают с оптимальными.