Chattaraj P.K. (Ed.) Quantum Trajectories

Подождите немного. Документ загружается.

84 Quantum Trajectories

where

is given by Equation 5.46 with θ replaced by α. In this representation the

wavefunction may be expanded in terms of a complete set of orthonormal spin

basis

functions Equation 5.7 for each k:

Ψ =



=1,2

(t)

(α

) (5.51)

where the product is antisymmetrized. To obtain the fermion ﬁeld dynamics we need

to choose special forms for the potentials, analogous to the oscillator potential in

the boson case. We choose A

= (0,

√

,0) = const., where B

= E

/ so

that A

√

(0,1,cosθ

), and V =−



. This implies a constant

“magnetic” ﬁeld B

= (0, 0, B

). With these assumptions, the rotator equation of

motion 5.49 becomes

∂ω

∂t



j,l

ijl

iI

Q (5.52)

and the Schrödinger Equation 5.50 is

i

∂Ψ

∂t



i,k

Ψ + B

Ψ. (5.53)

It is a simple matter to map this theory into more familiar language. We note that the

angular momentum operators obey the following commutation and anticommutation

relations:

[

]

−



iε

ijl

, [



]

−

= 0, [

]

= 2(/2)

, k = k



(5.54)

Making a Jordan–Wigner transformation [9, 10], these relations may be expressed

equivalently as an algebra of fermionic creation and annihilation operators. Thus,

deﬁning

= (1/)λ

(

− i

), a

†

= (1/)λ

(

+ i



(−2



/),

(5.55)

the new operators obey the anticommutation relations that deﬁne a fermion theory:

, a

†



]

= δ



, [a

, a



]

=[a

†

, a

†



]

= 0. (5.56)

The Hamiltonian in Equation 5.53 is given by Equation 5.39 and, using the deﬁnition

Equation 5.40 of the ﬁeld operator, the Hamiltonian takes the form Equation 5.42

but where the commutation relations Equation 5.41 are replaced by anticommutation

relations. This completes the derivation of the dynamics of a free quantum fermion

ﬁeld from the trajectory theory of a continuum of spin

Larmor rotators subject to

torques derived from the quantum potential.

Quantum Field Dynamics from Trajectories 85

5.6 CONCLUSION

We have established that quantized ﬁelds admit two complementary descriptions

which ﬁnd a natural interpretation in the language of hydrodynamics: an Eulerian

picture which corresponds to the Schrödinger picture of ﬁeld theory, and a Lagrangian

picture comprising a (continuously) many-“particle” system. In particular, we have

shown how the Eulerian notion of evolution (the history of ﬁelds at a space point) may

be derived from the Lagrangian one (the temporal sequence of ﬂuid elements passing

through that point). One may transform between the pictures using the Formulas 5.28

and 5.29 and their inverses. The dynamics of boson and fermion ﬁelds may be given

a common description based on a generalized Riemannian geometry.

This and similar investigations suggest that the deterministic trajectory may be

regarded as a foundational component of the quantum description and not merely

an optional element of interpretation. We may regard the approach as an alternative

method of “quantization,” characterized as follows: starting from a single particle,

pass to a continuum of particles and introduce an interparticle interaction (the second

term in brackets in Equation 5.15). Next, generalize to a Riemannian space with

external scalar and vector potentials. Finally, pass to an Eulerian description. The

method attributes a fundamental formal signiﬁcance to the quantum internal potential

energy (the interaction term), beyond its original purely interpretational aspect [6].

This formalism has a certain universal character in that its Lagrangian technique

of construction applies to a variety of quantum theories. Indeed, it may be applied

to other ﬁeld theories admitting representations in terms of conservation equations,

such as Maxwell’s equations [4]. A common feature in all these applications is the

appearance of the quadratic interaction term, the different cases being distinguished

by the choice of the conﬁguration space and the external potentials. This approach

thus brings to light a meaningful sense in which physical theories generally may be

said to exhibit “wave–particle duality.”

The spin

rotator model was proposed originally as a solution to the problem of

extending the de Broglie–Bohm theory to ﬁelds quantized according to fermion statis-

tics, a problem that had hitherto been regarded as unsolvable [11]. In that case, one

regards one set of angle variables θ

as preferential labels describing the actual state of

the system (we have explained elsewhere why the de Broglie–Bohm model, although

similar mathematically, should not be conﬂated with the constructive application of

trajectories [2]). Conceptually, the model follows the lead of Bohm’s treatment of the

electromagnetic ﬁeld in terms of oscillating normal coordinates (as described in the

second of his classic papers [12]), an elementary version of which has been presented

in Section 5.4. It thus has the beneﬁt of establishing a fermionic analog of the normal

mode decomposition of bosonic ﬁelds.

BIBLIOGRAPHY

1. R.E. Wyatt, Quantum Dynamics with Trajectories (Springer, New York, 2005).

2. P. Holland, Ann. Phys. (NY) 315, 505 (2005).

3. E. Madelung, Z. Phys. 40, 322 (1926).

86 Quantum Trajectories

4. P. Holland, Proc. R. Soc. A 461, 3659 (2005).

5. P. Holland, Found. Phys. 36, 369 (2006).

6. P.R. Holland, The Quantum Theory of Motion (Cambridge University Press, Cambridge,

1993).

7. P. Holland and C. Philippidis, Phys. Rev. A 67, 062105 (2003).

8. H. Lamb, Hydrodynamics, 6th edition (Cambridge University Press, Cambridge, 1932).

9. P. Jordan and E.P. Wigner, Z. Phys. 47, 631 (1928).

10. J.D. Bjorken and S.D. Drell, Relativistic Quantum Fields (McGraw-Hill, New York, 1966).

11. P.R. Holland, Phys. Lett. A 128, 9 (1988).

12. D. Bohm, Phys. Rev. 85, 180 (1952).

The Utility of Quantum

Forces

Gary E. Bowman

CONTENTS

6.1 Introduction.....................................................................................................87

6.2 From Schrödinger to Bohm.............................................................................88

6.3 Features of Quantum Force Mechanics ..........................................................89

6.3.1 General Remarks ................................................................................89

6.3.2 Quantum and Classical Forces............................................................90

6.3.3 Nature of the Quantum Force .............................................................90

6.4 States and Trajectories from Quantum Forces ................................................91

6.4.1 Uniform Forces...................................................................................91

6.4.2 On Gaussians ......................................................................................92

6.4.3 Linear Forces ......................................................................................92

6.5 Conclusion ......................................................................................................94

Acknowledgments....................................................................................................94

Bibliography ............................................................................................................94

6.1 INTRODUCTION

Utility:The condition, quality, or fact of being useful or beneﬁcial (The Shorter Oxford

English Dictionary)

Bohmian mechanics—the causal interpretation of quantum mechanics ﬁrst introduced

in completed form by David Bohm in 1952 [1,2]—is generally believed to be empiri-

cally equivalent to “standard” quantum mechanics. In principle, any result obtainable

in one should be obtainable in the other. It need not be true, however, that equivalent

results may be obtained with equivalent ease in the two interpretations, or that they

always render equally valuable physical insights.

Even within Bohmian mechanics there exist two formulations, utilizing different

tools and concepts: one in terms of Hamilton–Jacobi theory, the other in terms of

Newtonian classical mechanics. I will call these, respectively, the HJ (Hamilton–

Jacobi) and QF (quantum force) formulations of Bohmian mechanics. Both must lead

to equivalent physics, but—much like the contrast between Bohmian and standard

quantum mechanics—this need not imply that they offer equivalent calculational tools

or physical insights.

88 Quantum Trajectories

Herein I do not argue which interpretation of quantum mechanics offers the correct

picture of the world, nor do I advocate one formulation of Bohmian mechanics over

the other. My goal is less fundamental, more utilitarian: to illustrate that the QF

formulation of Bohmian mechanics offers distinct mathematical and conceptual tools

that are unavailable in either the HJ formulation or in standard quantum mechanics.

Thus, the goal is not to show that the QF formulation is inherently superior to the

HJ formulation, but to show that in some cases the former offers greater utility.

Section 6.2 shows how Bohmian mechanics arises from the Schrödinger equation.

Section 6.3 discusses general conceptual and mathematical features of the QF formu-

lation. Section 6.4 illustrates how the quantum force formulation may be applied to

trajectories and quantum states. Section 6.5 presents a brief summary and conclusions.

6.2 FROM SCHRÖDINGER TO BOHM

The starting point for single-particle, non-relativistic Bohmian mechanics is the time-

dependent Schrödinger equation:

i

∂Ψ(x, t)

∂t

−

∇

Ψ(x, t) + V Ψ(x, t). (6.1)

Since Ψ(x, t) is a complex function, it may be written in polar form, Ψ(x, t) =

R(x, t) exp(iS(x, t)/), where the modulus, R, and the phase, S/, are real functions.

Substituting this form into the Schrödinger equation, taking derivatives, and separat-

ing the real and imaginary parts, we obtain the following two coupled equations:

−

∂S

∂t

(∇S)

+ V −





∇



, (6.2)

∂





∂t

=−∇·





∇S



. (6.3)

Note that R

=|Ψ|

, the position probability distribution. Equation 6.3 is a continuity

equation for probability, while Equation 6.2 closely resembles the classical Hamilton–

Jacobi equation,

−

∂S

∂t

(

∇S

)

+ V , (6.4)

where S

denotes Hamilton’s principal function [3].

Only now is Bohm’s alternative interpretation introduced, by choosing to regard

Equation 6.2 as analogous to the classical Equation 6.4. In classical Hamilton–Jacobi

theory we obtain p

=∇S

, where p

is the momentum of a classical particle. In

Bohmian mechanics, then, we have the analogous guidance condition:

p =∇S. (6.5)

Here p describes the momentum of a particle on a Bohmian trajectory, and the quan-

tum dynamics describes an ensemble of possible trajectories, corresponding to an

The Utility of Quantum Forces 89

ensemble of possible initial conditions, of a real particle with continuously existing

and well-deﬁned dynamical properties. Equation 6.5 is the deﬁning equation of the

HJ formulation.

The last term in Equation 6.2, the analog of which does not appear in Equation 6.4,

is denoted Q,

Q =−





∇



. (6.6)

In Bohmian mechanics Q is often regarded as an additional potential energy, and

referred to as the quantum potential. We may then associate with Q a quantum force,

denoted F

=−∇Q. (6.7)

With Q and F

in hand, we may discuss Bohmian mechanics in terms of a Newtonian

formulation, with the total (classical plus quantum) force given by:

F = F

+ F

=−∇(V + Q). (6.8)

Equations 6.6, 6.7, and 6.8, along with Newton’s second law of motion (into which

F is substituted) form the basis for the QF formulation of Bohmian mechanics, or

simply QF mechanics.

Forces act on particles, and in the ensemble of Bohmian trajectories that comprise a

pure state, only one is occupied by an actual particle—although which one is unknown.

Nevertheless, a Bohmian ensemble must evolve as though every trajectory is occupied

by a particle subject to classical and quantum forces, evaluated at that trajectory. In

what follows, then, we can think of forces on, or the momenta of, trajectories.

Is one formulation “correct” and the other “wrong?” Leaving aside precisely what

such a question could even mean, the fact is that QF mechanics is acceptable as a means

of obtaining results. As Bohm himself said [1, p. 170]: “use of the Hamilton–Jacobi

equation in solving for the motion of the particle is only a matter of convenience . . .

in principle, we can always solve directly by using Newton’s laws of motion and the

correct boundary conditions.”

6.3 FEATURES OF QUANTUM FORCE MECHANICS

6.3.1 GENERAL REMARKS

In Bohmian mechanics, the quantum state of interest is typically calculated by

conventional means. The Bohm trajectory behavior may then be investigated: the

squared wavefunction (|ψ|

) is the position probability distribution, and thus the

Bohm trajectory position distribution; the momentum distribution is obtained through

Equation 6.5, the guidance condition. In this approach, QF mechanics plays a periph-

eral role, if any.

In some cases, however, QF mechanics may be used to obtain the time-dependent

behavior of the quantum state and the Bohm trajectories. And even when it cannot, it

90 Quantum Trajectories

can provide a means to think about quantum behavior in an approximate or qualitative

sense; QF mechanics offersa conceptual—not just abstract and mathematical—means

to understand a system’s behavior.

I believe, and hope to convince you, that acquiring some familiarity with key fea-

tures of QF mechanics can be worthwhile, quite apart from whether one’s loyalties

might otherwise lie with standard quantum mechanics or Bohm, with one form of

Bohmian mechanics or the other.

First a qualitative remark: QF mechanics is expressed in terms of Newton’s second

law of motion, that is, in terms of concepts, tools, and language that most of us have

been using since our earliest exposure to physics. These can be rather easily imported

for use in QF mechanics.

6.3.2 Q

UANTUM AND CLASSICAL FORCES

Even in standard quantum mechanics, time evolution may be thought of as occurring

due to both quantum-mechanical effects and the effects of the classical potential

(i.e., due to classical forces). But there may be no way to separate these effects.

Indeed, it is unclear what it could even mean to separate quantum and classical

effects in standard quantum mechanics, where concepts such as particle, trajectory,

and force—the fundamental stuff of classical mechanics—have no clear meaning.

It is a particular virtue of QF mechanics that we may disentangle classical and

quantum effects. A remarkable feature is apparent in Equation 6.8: evidently the

total force—which governs time evolution of the Bohm trajectories, and thus of

the state—is separable into quantum and classical contributions. Another notable

feature is evident in Equations 6.6 and 6.7: F

depends on the modulus, R, but not

the phase, S.

Yet both the separability of forces and F

’s phase independence hold only in a

limited sense. A complicated interplay exists between classical and quantum forces.

Over time, F

will alter the momentum distribution, and thus R,soF

at a given

trajectory will differ from what it would have been if F

= 0. In this sense F

does depend on F

, despite separability. Similarly, F

is formally independent of

the phase, but again, the momentum distribution (i.e., the phase) will alter R, and

thus F

, over time. (In Section 6.4 I consider cases where force separability and

phase independence prove useful despite these complications.)

6.3.3 N

ATURE OF THE QUANTUM FORCE

Newton’s second law is a second-order ordinary differential equation, but to imple-

ment it in QF mechanics we must obtain F

. From Equations 6.6 and 6.7, we have:



2mR



∇

R − R

−1

∇

R∇R



. (6.9)

Equation 6.6 may suggest that inspection of R’s curvature easily yields information

about F

. Equation 6.9 suggests otherwise: R may be a highly complicated function,

The Utility of Quantum Forces 91

and F

is proportional to ∇

R − R

−1

∇

R∇R. Thus, even qualitative statements

about F

’s strength, or indeed just its direction, will likely require careful analysis; a

cursory inspection of the wavefunction invites error.

In principle, QF mechanics offers one approach to numerical time evolution. But

even simple, low-order derivatives can lead to unreliable numerical results, and Equa-

tion 6.9 includes ∇R, ∇

R, and ∇

R. Thus, while QF mechanics remains one option

for numerical calculations, it does not seem a promising one.

6.4 STATES AND TRAJECTORIES FROM QUANTUM FORCES

For two simple potentials, QF mechanics easily leads to exact results. In what fol-

lows, these two cases will be presented in broad outline form. Detailed treatments

are available elsewhere; the primary goal here is to illustrate the features discussed

in Section 6.3.

6.4.1 U

NIFORM FORCES

Forces that are uniform in space, that is, that have no spatial dependence, are easily

treated using QF mechanics (for a full discussion, see Ref. [4]). In this case, F

imparts an identical momentum boost to each Bohmian trajectory.As a result, F

will

translate the modulus R, but it cannot alter the momenta of the Bohmian trajectories

relative to each other, and thus it cannot alter R’s shape. Because F

depends only on

R’s shape, and F

cannot alter that shape, F

must remain identical for corresponding

trajectories in the free and forced states.

The preceding argument relies only on the spatial uniformity of F

. Thus our

result still holds even if we introduce an arbitrary time dependence into our spatially

uniform F

. Thus, we can solve for the problem of an arbitrary initial state subject to

an arbitrarily time-dependent, spatially uniform force, by solving the corresponding

free-particle problem, and then simply “adding on” the classical translation and boost

that the uniform force imparts.

While the foregoing is qualitative, we can nevertheless construct the formal

expression for the state from the fact that in Bohmian mechanics the phase has a

straightforward interpretation in terms of the momentum distribution of the trajecto-

ries. In particular, if Ψ

(x, t) is the free-particle state obtained above, then the state

subject to our uniform force, denoted Ψ(x, t), is simply

Ψ(x, t) = Ψ

(x −∆x

(t), t) exp(i∆p

(t) · x/) exp(iS

/), (6.10)

where ∆x

and ∆p

are the classical displacement and momentum change, respec-

tively, due to F

. (The exponent S

/, which may depend on t but not x, may be

readily and explicitly calculated, as shown in Ref. [4].)

In sum, the only effects of an arbitrarily time-dependent, spatially uniform classical

force are to translate and boost the corresponding free-particle quantum state as it

would a classical particle.

92 Quantum Trajectories

6.4.2 ON GAUSSIANS

In Section 6.4.3 I focus on Gaussians subject to linear classical forces. Before doing

so, it’s worth considering Gaussians rather generally.

Consider a one-dimensional state with a Gaussian modulus centered at x = x

, i.e.,

Ψ(x) ∝ e

−β(x−x

)

. Here β characterizes the Gaussian’s width; for a time-dependent

width, β = β(t). The quantum force is

(x) =

4

(x −x

), (6.11)

From Equations 6.6 and 6.7, F

is determined only by the modulus, and depends on

position relative to the state itself, but not on its overall location, or its motion, or the

momentum distribution.

Gaussians often seem particularly well suited to quantum-mechanical calculations.

As one simple example, many introductory quantum textbooks solve exactly for the

time evolution of a free-particle Gaussian—but not for other initial states.

Why not? Probably because it’s hard, or impossible, to do so. And why is that?

Why are Gaussians so “nice” for the free-particle, and for other cases as well? I am

unaware of an answer—except in the context of QF mechanics, wherein we see that

Gaussians possess a very special property: their quantum force is linear. This special

property will play a crucial role in the next section.

6.4.3 L

INEAR FORCES

Now consider a time-independent, spatially linear classical restoring force (a simple

harmonic oscillator), and an initial state with a Gaussian modulus, and a phase at

most quadratic in x. In this case both F

and F

, and thus the total force, F , are

linear in x. As a result, our Gaussian will remain a Gaussian (as shown in Ref. [5]).

The Gaussian’s peak motion will be exactly classical. This can be shown through

explicit calculation or from Ehrenfest’s theorem [6]. It also arises quite simply in QF

mechanics.

Because our Gaussian remains a Gaussian, Equation 6.11 holds for all t, which in

turn implies that F

= 0 at the peak (x = x

) for all t . Thus the peak’s motion, and

therefore the state’s overall motion, is strictly classical—determined by F

alone.

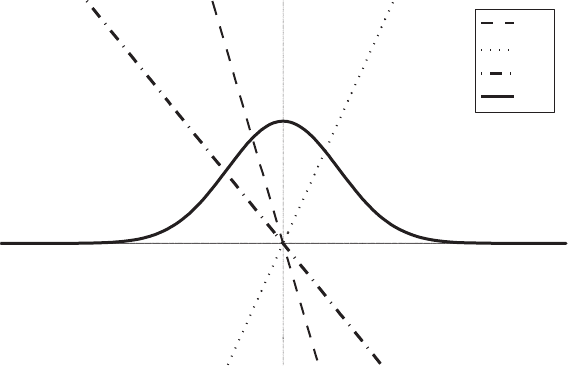
What of the Gaussian’s width? Figure 6.1 illustrates the situation in QF mechan-

ics. F

(dashed line) is a restoring force; from Equation 6.11, F

(dotted line) must

be linear and expansive, i.e., an anti-restoring force. If, as in Figure 6.1, the slope

of F (dotted-dashed line) is negative, then the Gaussian is subject to a net restoring

force; if positive, it is subject to a net anti-restoring force.

The dynamics of the Gaussian’s width depend on F , the total force, and thus (in

contrast to its overall motion) on F

and F

. In particular, the relative behavior of

two trajectories in the Gaussian is determined by the total force difference between

the trajectories, and thus by the slope of F .

In addition to F , the width dynamics will depend on the state’s initial (width)

conditions, so let us assume it is narrowing at t = 0. This narrowing has no effect

The Utility of Quantum Forces 93

|Ψ|

FIGURE 6.1 Classical, quantum, and total forces for a Gaussian centered at x = 0. Here the

classical force is linear and restoring.

on F

. But β (in Equation 6.11) increases, so F

’s slope, also, increases. As the

state narrows this process continues, and F eventually becomes an anti-restoring

force (its slope becomes positive). This eventually results in the state’s expansion,

with decreasing F

, until F once again becomes a restoring force. This, in turn,

eventually leads to the packet again narrowing—and so the process repeats itself. It

turns out that for the harmonic oscillator the width simply oscillates with half the

classical period [5]. Note that though the dynamics of the width involve both F

and F

, the problem is essentially classical.

Now let our linear F

be either restoring or anti-restoring, with arbitrary time

dependence (this case is discussed in Ref. [7]). Consider ﬁrst the overall motion.

F remains linear for all t, which is sufﬁcient to insure that a Gaussian remains a

Gaussian [5, 7]. Thus, Equation 6.11 still holds for all t, and F

= 0 at the peak for

all t. So the state’s overall motion is again classical—determined by F

alone (and

again in accord with Ehrenfest’s theorem).

As before, the width behavior is determined by the slope of F . Naturally, for

restoring or anti-restoring and with arbitrary time dependence, we cannot expect

simple behavior, as for the harmonic oscillator. Still, the basic method of solution,

along with the accompanying conceptual picture, remain valid.

Evidently QF mechanics has reduced our Gaussian’s time evolution to

• determination of the motion of the Gaussian’s peak,

• time evolution of the Gaussian’s width.

That is, we now have two independent, essentially classical problems.

In Ref. [7] we will show, through simple QF arguments, that the only effect of

adding a uniform classical force to a linear classical force is to change the state’s