Цейтлин М.Б., Кац А.М. Лампа с бегущей волной

Подождите немного. Документ загружается.

/Iли вычисления усиления необходимо найти связь

м* Фму I) и Ь\ при больших значениях параметра С. Она

цмжи! быть найдена из соотношений (ПГШа) и (111.43).

1ложный расчет дает

Щ ъ = 2ь

-У2Ь

-f Ь

су + 4b\q . (III.46)

111,4, МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ

Приближенный анализ взаимодействия электронного

Цвиокм с бегущей электромагнитной волной может быть

ЬиИФДен методом последовательных приближений. За-

1йн пулевое приближение для поля, можно проинтегри-

Кш гь уравнения движения электрона и определить его

Смещение в ВЧ поле. Используя закон сохранения заря-

flii, можно вычислить переменный ток, обусловленный

(цидоПствием на пучок поля волны. Этот ток в свою оче-

К|Д|| возбуждает в волноводной системе поле, которое

•Мнете с начальным полем дает первое приближение.

Продолжая этот процесс, можно получить второе при-

ближение для ВЧ поля, третье и т. д.

Вычислим усиление в ЛБВ методом последователь-

ных приближений, 'причем для простоты предположим,

•но

затухание в системе и силы кулоновского расталки-

млнии в пучке пренебрежимо малы [6].

11усть нулевому приближению соответствует поле не-

|м)1мущенной волны, амплитуда которого при z=0 рав-

lut ммплитуде входного сигнала:

| E

t) =

sm{<*>t

— $z). (III.47)

Подставим в правую часть уравнения движения элек-

трона

Щ-ШЯ

соотношение (III.47),'причем в качестве исходного выра-

жения для z возьмем выражение, соответствующее не-

мачмущенному движению электрона, z=Vo(t—to), где

U) - время влета электрона в систему. Тогда обозначая

Чфрез 5 высокочастотное смещение электрона (т. е. рас-

стояние от невозмущенного положения), получаем

Sin К +

(*ф -

)

{t if§, (III.48)

ИЗ

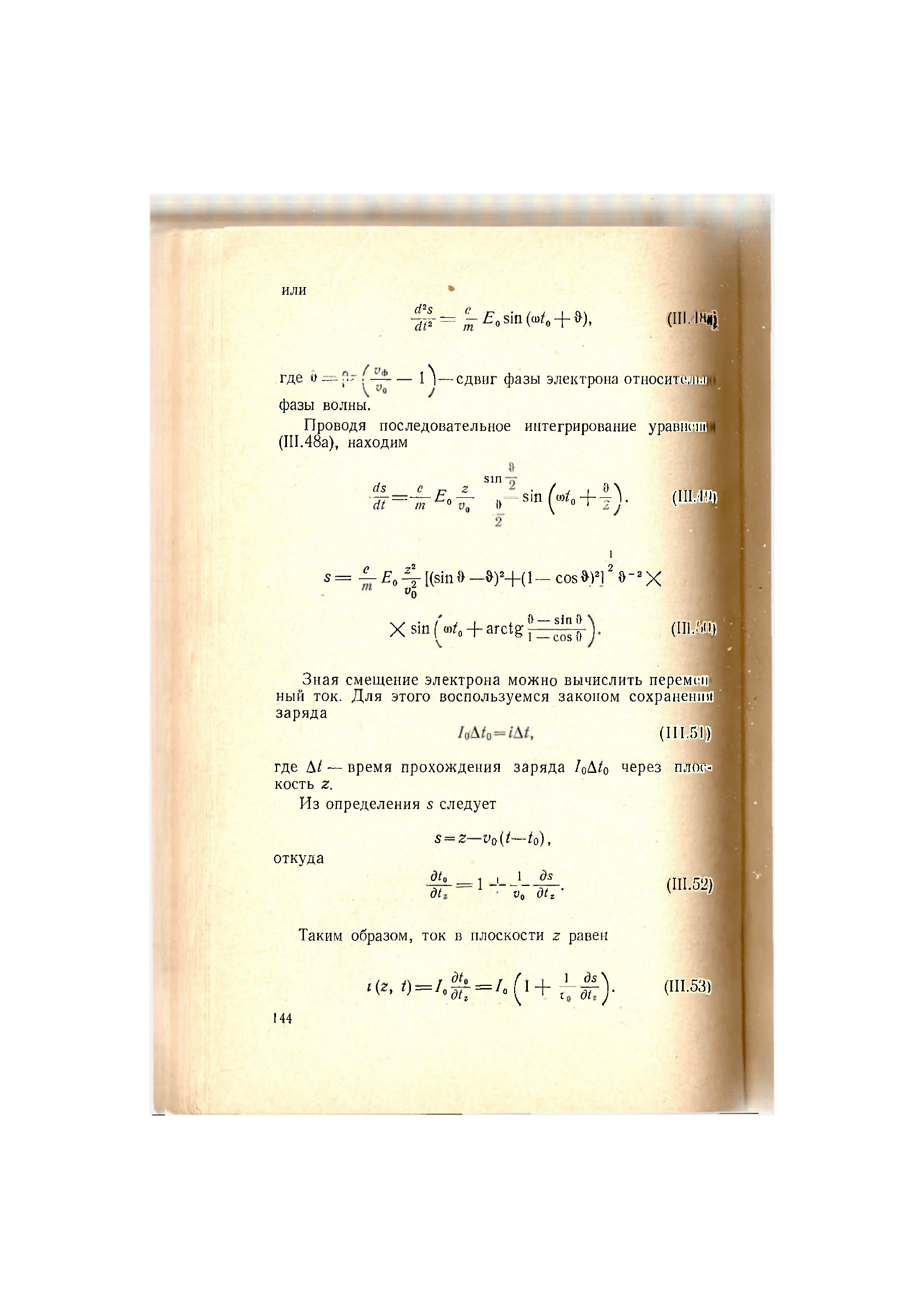
или

s е

sin « + &),

(III.IM*)

где — — О—сдвиг фазы электрона относителы

фазы волны.

Проводя последовательное интегрирование уравнеш

(III.48а), находим

е г? z

—

sin

dt — m

sin^o+Ж (111.4)1)

s=±-E

4- [(sin

-&)Ч-(1 - cos

& -

X sin ((o/

-f-arctg

0 — sin 0

1 — cos b

(III

50)

Зная смещение электрона можно вычислить перемен

ный ток. Для этого воспользуемся законом сохранения

заряда

(111.51)

где Д/ — время прохождения заряда IoAto через плосЛ

кость z.

Из определения 5 следует

откуда

s=z—v

(t—t

)

j , 1_ ds

(111.52)

Таким образом, ток в плоскости z равен

.144

1(г

, <>=/.£=/„ (

1 + 1

L|i).

(111,531

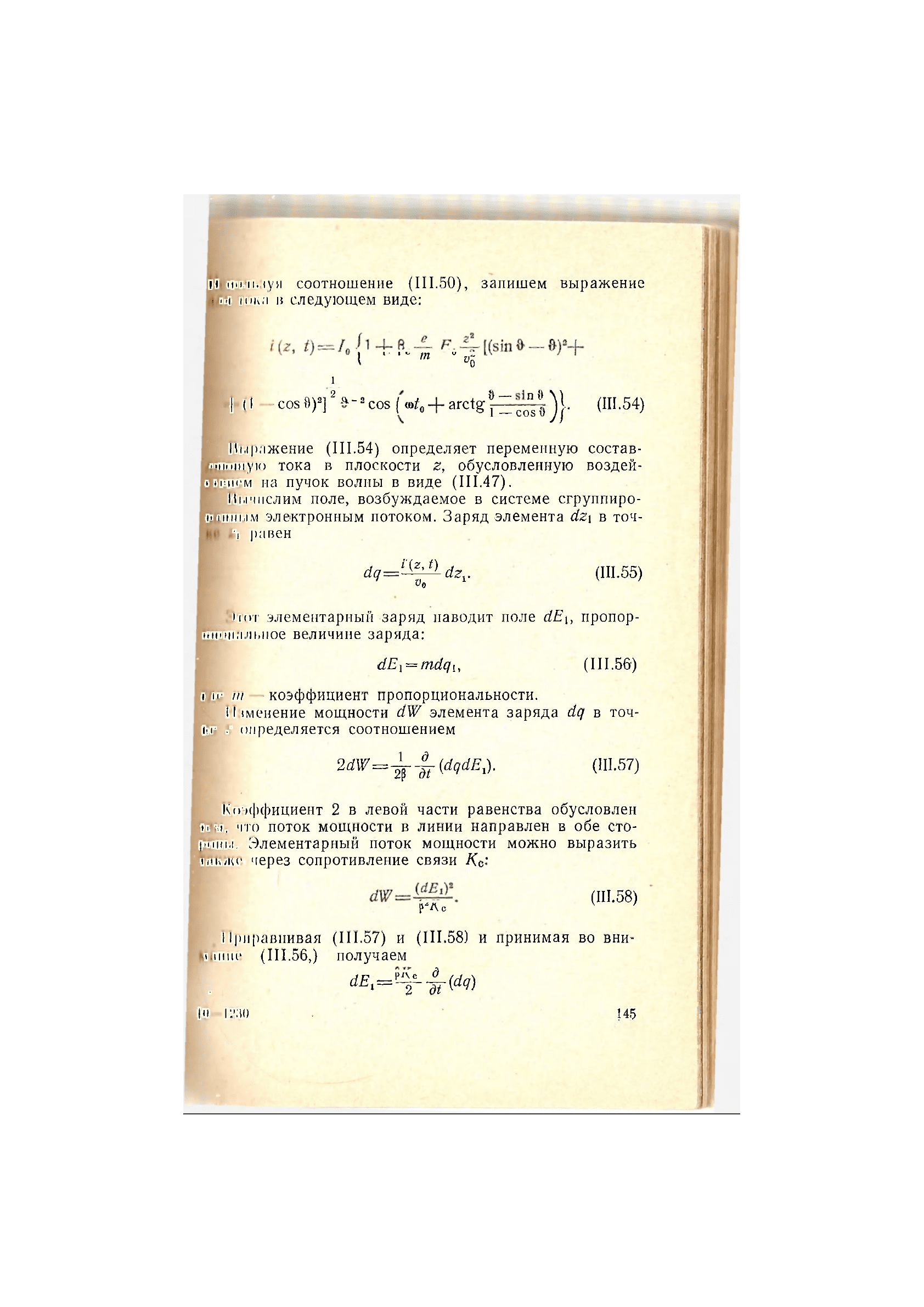
шцолизуя соотношение (III.50), запишем выражение

/Ни

юка в

следующем виде:

cos

f>)

]

cos

arctg ^Zco

t)}-

РЙ

Иыражение (III.54) определяет переменную состав-

'имищую тока

плоскости

обусловленную воздей-

ШИем

на

пучок волны

виде (111.47).

Исчислим поле, возбуждаемое

системе сгруппиро-

ЦнМНЫМ электронным потоком. Заряд элемента

dz\ в

точ-

fi равен

dq=

i^-dz

(III.55)

Этот элементарный заряд наводит поле

dE\,

пропор-

циональное величине заряда:

dEi

mdqu (111.56)

i mi

— коэффициент пропорциональности.

Изменение мощности

элемента заряда

dq в точ-

определяется соотношением

В i^iifti

(IIL57)

Коэффициент

2 в

левой части равенства обусловлен

и м,

что

поток мощности

линии направлен

в обе сто-

роны. Элементарный поток мощности можно выразить

мкже через сопротивление связи

Кс'

(111.58)

Р А с

Приравнивая (111.57)

(111.58)

принимая

во вни-

мание (111.56,) получаем

Г ррЩ

III

1230 145

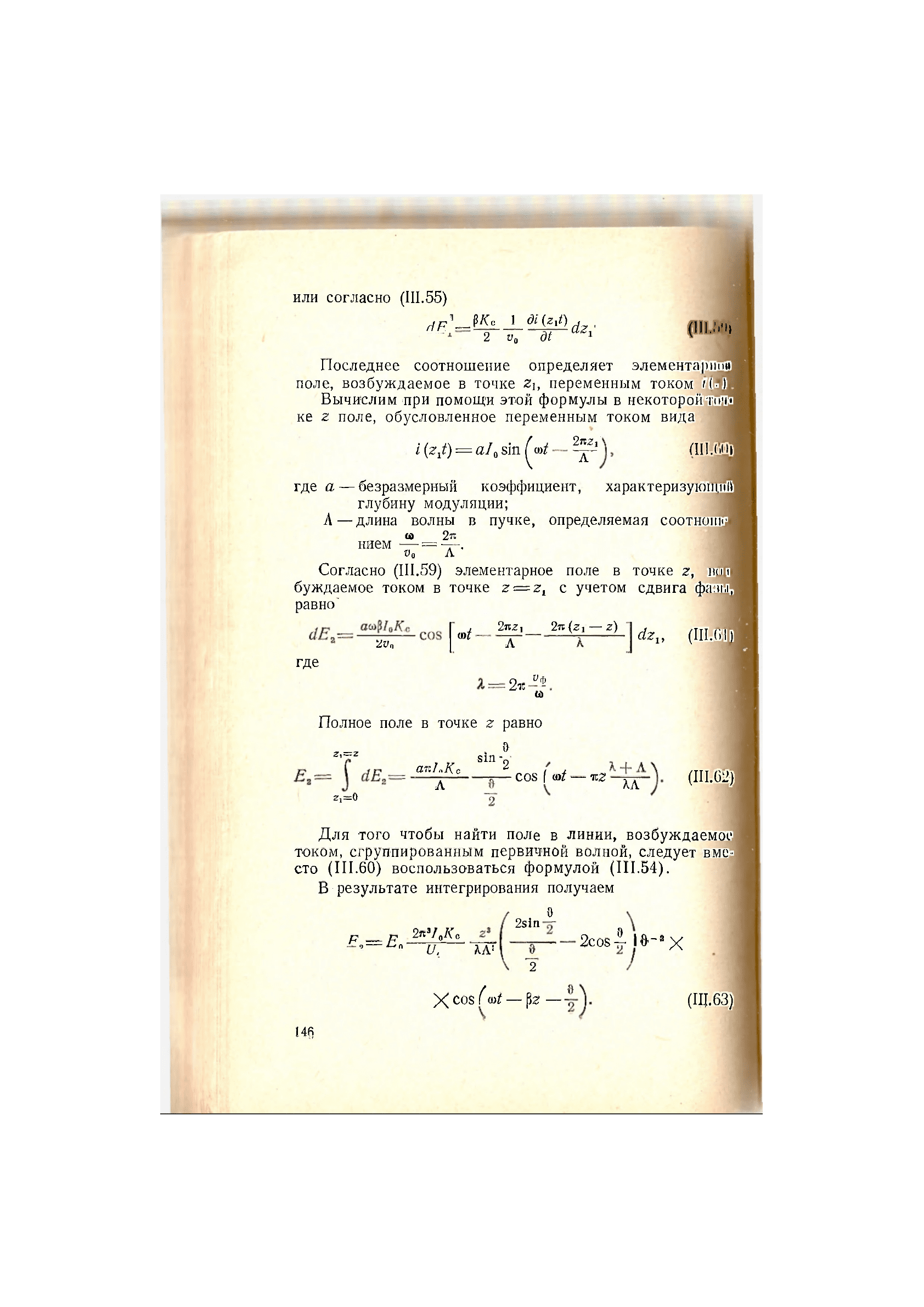
или согласно (III.55)

'^ШКс^ЩЖЩ

2 v

(Ш.ПЯ

Последнее соотношение определяет элементарно!

поле, возбуждаемое в точке z

переменным током pi/)

Вычислим при помощи этой формулы в некоторой ТОв

ке z поле, обусловленное переменным током вида

i (z

t) = а/

sin ^(о/

2 nzi

М(Юк

где a — безразмерный коэффициент, характеризующий

глубину модуляции;

А — длина волны в пучке, определяемая соотношм

со 2л

нием —=-т-.

Согласно (III.59) элементарное поле в точке z

вон*

буждаемое током в точке z = z

с учетом сдвига

фазы,

равно'

2nz

2n(zi—z)

ZVii

001

где

2it

(111.61)

Уф

со

Полное поле в точке г равно

2Г,=2

sin

anLKc *

COS ( ait —

7ZZ

лл

(111.62)

Для того чтобы найти поле в линии, возбуждаемое

током, сгруппированным первичной волной, следует вме-

сто (111.60) воспользоваться формулой (111.54).

В результате интегрирования получаем

р р 2я

/Сс

О П

Г 7

и,

ЛЛ

{

2sin

2cos~ &~

COS

f atf — $Z —

(11| 63}

на

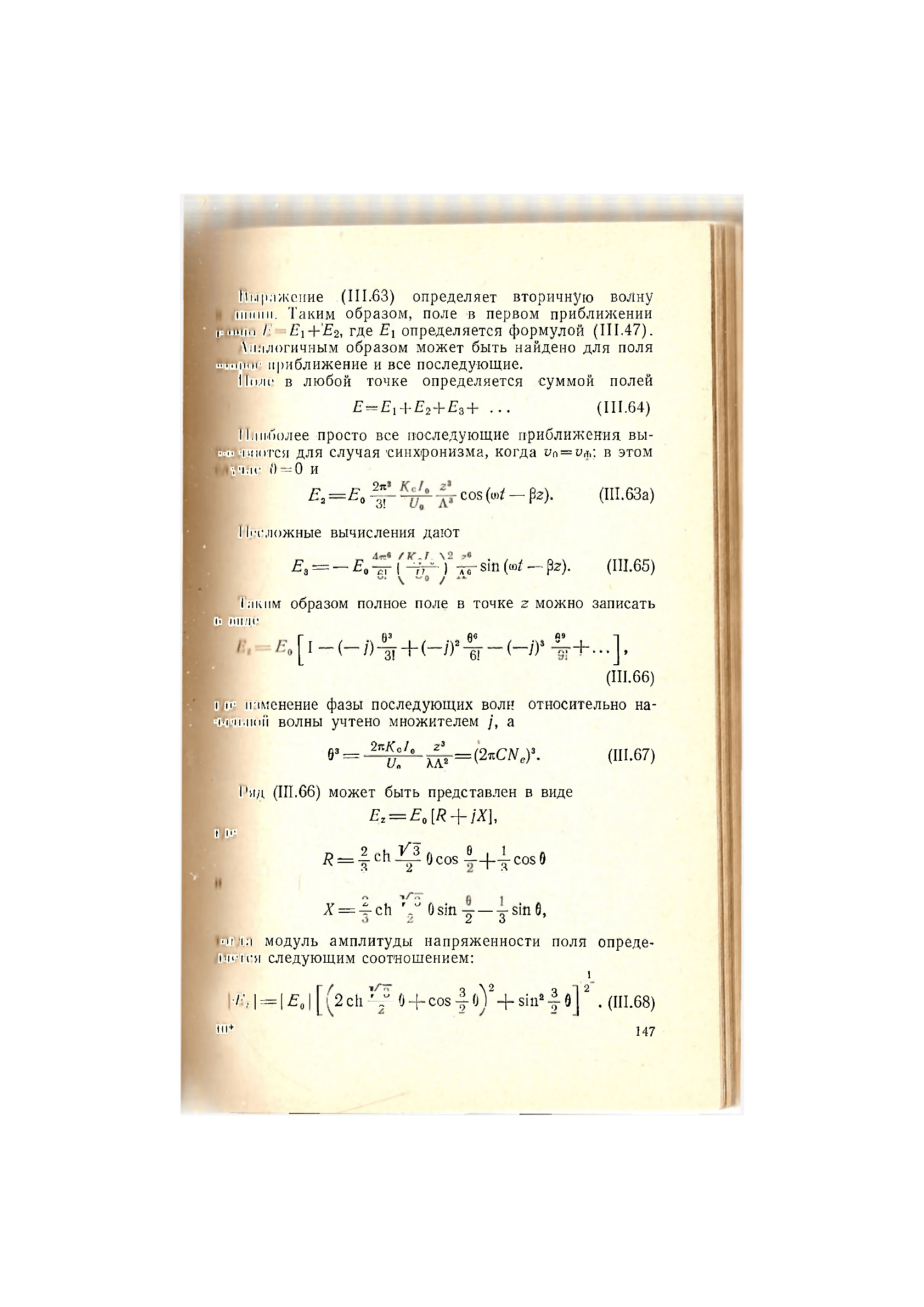
Выражение .(111.63) определяет вторичную волну

линии. Таким образом, поле в первом приближении

•яино /:'«=£'I+

2, где Е\ определяется формулой (111.47).

Аналогичным образом может быть найдено для поля

Мути* приближение и все последующие.

Моле в любой точке определяется суммой полей

Е=Е

+Е

+ ... (II 1.64)

Мшиболее просто все последующие приближения вы-

•Цглиются для случая 'синхронизма, когда В этом

учис 0=0 и

Щ Е

=Е.%COS (®t - pz). (III.63A)

^сложные вычисления дают

Н Е, = - Е

sin И - И- (IH.65)

Таким образом полное поле в точке z можно записать

и МИДе

[

A3 06 09 "I

1 - (-

^ + (-/)'^ ~ (-/)'

• • •

] '

Щ (Ш.66)

in' изменение фазы последующих волн относительно на-

Шьиой волны учтено множителем /, а

I в'= ^ =(2nCN

)\ (111.67)

Ряд (111.66) может быть представлен в виде

= E

[R + jX],

НАГ

Гз

|CHJ^0COS 1+4 COS 0

• Х = 0sin -J—jsin6,

О Г да модуль амплитуды напряженности поля опреде-

лится следующим соотношением:

•1Ц = \Е

2 ch

+ cos f вУ + sin

. (111.68)

Hi* 147

Выражение (1П.68) определяет зависимость усилении

ЛБВ от длины участка взаимодействия при v$=v

дли

пренебрежимо малого пространственного заряда и при

отсутствии затухания в 'системе. В работе [7] показано,

что решение задачи о взаимодействии электронного по

тока с бегущей волной постоянной амплитуды эквипи»

лентно первому приближению. Метод последовательный

приближений нашел широкое применение для аналим

различных типов взаимодействия электронного поток*

с электромагнитным полем в книге В. Н. Шевчика |Н),

ГЛАВА IV

IHИОННЫЕ УРАВНЕНИЯ НЕЛИНЕЙНОЙ ТЕОРИИ

1ДИМОДЕЙСТВИЯ ЭЛЕКТРОННОГО ПОТОКА

(! БЕГУЩЕЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНОЙ

IV.1, ВВЕДЕНИЕ

И предыдущих главах рассматривалась линейная тео-

|пн| ЛБВ, справедливая для режима малых амплитуд,

•оиущения, положенные в основу линейной теории, не

•livui справедливы в реальных приборах. Это особенно

Вносится к лампам средней и большой мощности. В этом

мумие амплитуды переменных составляющих скорости,

|o№t и плотности пространственного заряда сравнимы

not>твегствующими постоянными составляющими, и по-

«»му в уравнениях, описывающих электронный поток,

mii.

пренебрегать произведением переменных величин.

И режиме «больших амплитуд электроны под действием

высокочастотного поля сильно изменяют свою первона-

|й 'И.ную скорость, что приводит к обгону электронов. По-

Ному к такому электронному потоку не применимы урав-

•#МИЯ гидродинамики идеальной жидкости. В связи

I» итнм анализ работы ЛБВ в режиме больших ампли-

туд может б^ыть проведен только на основе нелинейной

Нории. Результаты нелинейной теории дают возмож-

Моп ъ определить максимальную выходную мощность

JIliB, а также зависимость коэффициента усиления от

Ьличины входного сигнала.

Впервые уравнения нелинейной теории ЛБВ были

сформулированы в [1]. При выводе этих уравнений не

учитывался пространственный заряд и задача решалась

1 приближении малых значений 'параметра усиления.

Дальнейшее обобщение уравнений -нелинейной теории

Проведено в работах [2—4], где учтены поле пространст-

.149

ВёМного Заряда и затухайие в линии. Ё работах (3, 1|,

кроме того, задача решена для больших значений парм

метра усиления. Подробный анализ этих работ дан щ

третьем параграфе настоящей главы.

Исходя из несколько других позиций, выведены об!

новиые уравнения в работе [5], в которой учтены прост*]

ранственный заряд и затухание в линии. Эти уравнении

выведены в предположении малых значений <парамеТ|>|П

усиления. Основные результаты расчета по этим урин»

нениям приведены в работах [6, 7].

IV.2. ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ. ЗАКОНЫ

СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ

В этом параграфе уравнения нелинейной теории Л'Б

И,

полученные в [5], обобщаются на случай больших значок

ни'й параметра усиления.

При выводе основных уравнений нелинейной теории

ЛБВ примем следующие допущения:

1) рассматриваются «гладкие» системы, т. е. такии

системы, неоднородности которых не сказываются ни

взаимодействии электромагнитной волны с электронным

потоком;

2) скорость электронов и плотность конвекционного

тока имеют только продольную составляющую;

3) скорость электронов намного меньше скорости cneJ

та, так что релятивистскими эффектами можно npeiioi

бречь;

4) замедляющая система идеально согласована ил

концах, так что отражение электромагнитной энергии от-

сутствует.

В режиме больших амплитуд конвекционный ток пуч-

ка является несинусоидальной (ню периодической) функ-

цией времени и, следовательно, содержит бесконечное

множество временных гармоник основной частоты. Тогда

конвекционный ток пучка может быть разложен в ряд

Фурье [б]

(IV

Л)

где /о — среднее за период значение тока;

ik — комплексная амплитуда k-и гармоники.

.150

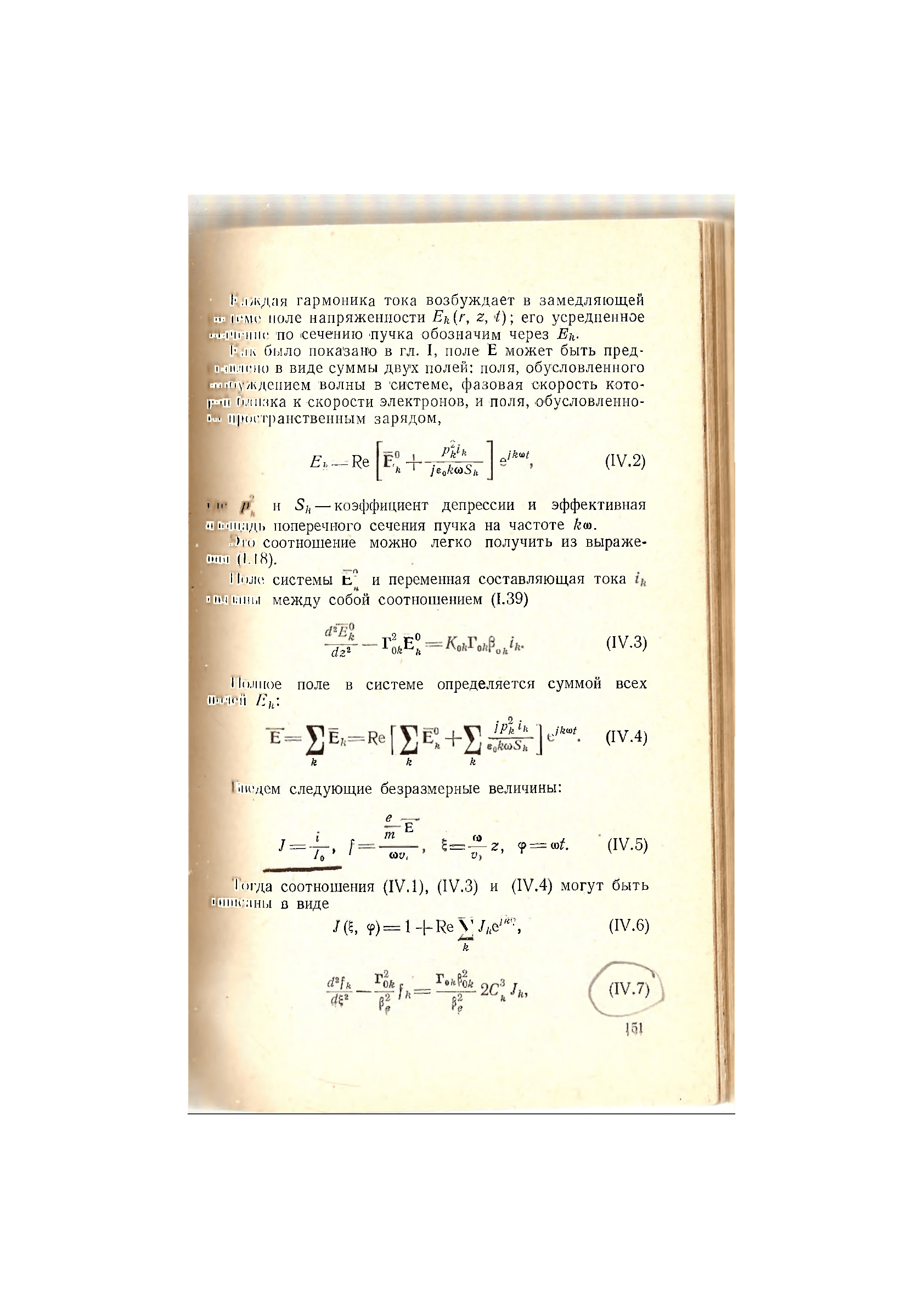
Каждая гармоника тока возбуждает в замедляющей

•ГГОМе поле напряженности Ek{r, z, i)\ его усредненное

•щоние 'по сечению пучка обозначим через Ей-

а к было пока'зано в гл. I, поле Е может быть пред-

•имено в виде суммы двух полей: поля, обусловленного

•Суждением волны в системе, фазовая скорость кото-

|hhi близка к скорости электронов, и поля, обусловленно-

fM пространственным зарядом,

Еъ — Re

'к

k(»>Sk

•jm

(IV. 2)

i itn p

и S

— коэффициент депрессии и эффективная

рищадь поперечного сечения пучка на частоте km.

Это соотношение можно легко получить из выраже-

нии (1.18).

11оле системы и переменная составляющая тока

1имшшы между собой соотношением (1.39)

2 рО

о kPh

(IV.3)

11олное поле в системе определяется суммой всех

ИШШЙ Е

\р\ i

k k k

Jktat

(IV.4)

^едем следующие безразмерные величины:

/=-f. f

(О

СОУг

=—г,

= wt.

(IV. 5)

Тогда соотношения (IV.l), (IV.3) и (IV.4) могут быть

Иниисаны в виде

/(?,

<f)

+ Re 7

(IV.6)

e _ о

-^PoS^ft

Jk<?

(IV,H)

Амплитуды гармоник конвекционного тока определи)

ются как коэффициенты ряда Фурье:

h=±\je->

4<p.

Уравнение движения электрона в безразмерных коор

динатах запишется в виде

= Re

h+i

k<a

=T~7I

ih 9

(IV.1I

•Очевидно, что безразмерная координата £ зависит

не только от текущей фазы ф, но и от момента влети

электрона в 'пространство взаимодействия. Это вр|м>1

определяется начальной фазой или фазой влета фо- Сло|

довательно,

= S(?, *•). (IV.10)

В режиме больших амплитуд имеет место обгон.

электронов, т. е. в данном сечении (£=const) одному

значению текущей фазы ф может соответствовать не!

сколько значений фазы влета щ. Та-ким образом, ф

яв-1

ляется неоднозначной функцией ф и

Запишем закон сохранения заряда

Jdq)=dq>o.

(IV.11)

Такая форма записи справедлива для односторон-

него движения электронов, которое, вообще говоря, нф,

всегда выполняется. В дальнейшем примем за независим

мые переменные безразмерное расстояние

и начальную

фазу влета электрона в пространство взаимодействия.

Поэтому соотношение (IV. 10)^ за пишем в виде

Ф=Ч>(£, Фо).

(IV.

12)

.152