Цейтлин М.Б., Кац А.М. Лампа с бегущей волной

Подождите немного. Документ загружается.

ШШШРяНI

Которое позволяет рассчитать электрическую длину на

первой обратной гармонике для любых параметров ЛБВ.

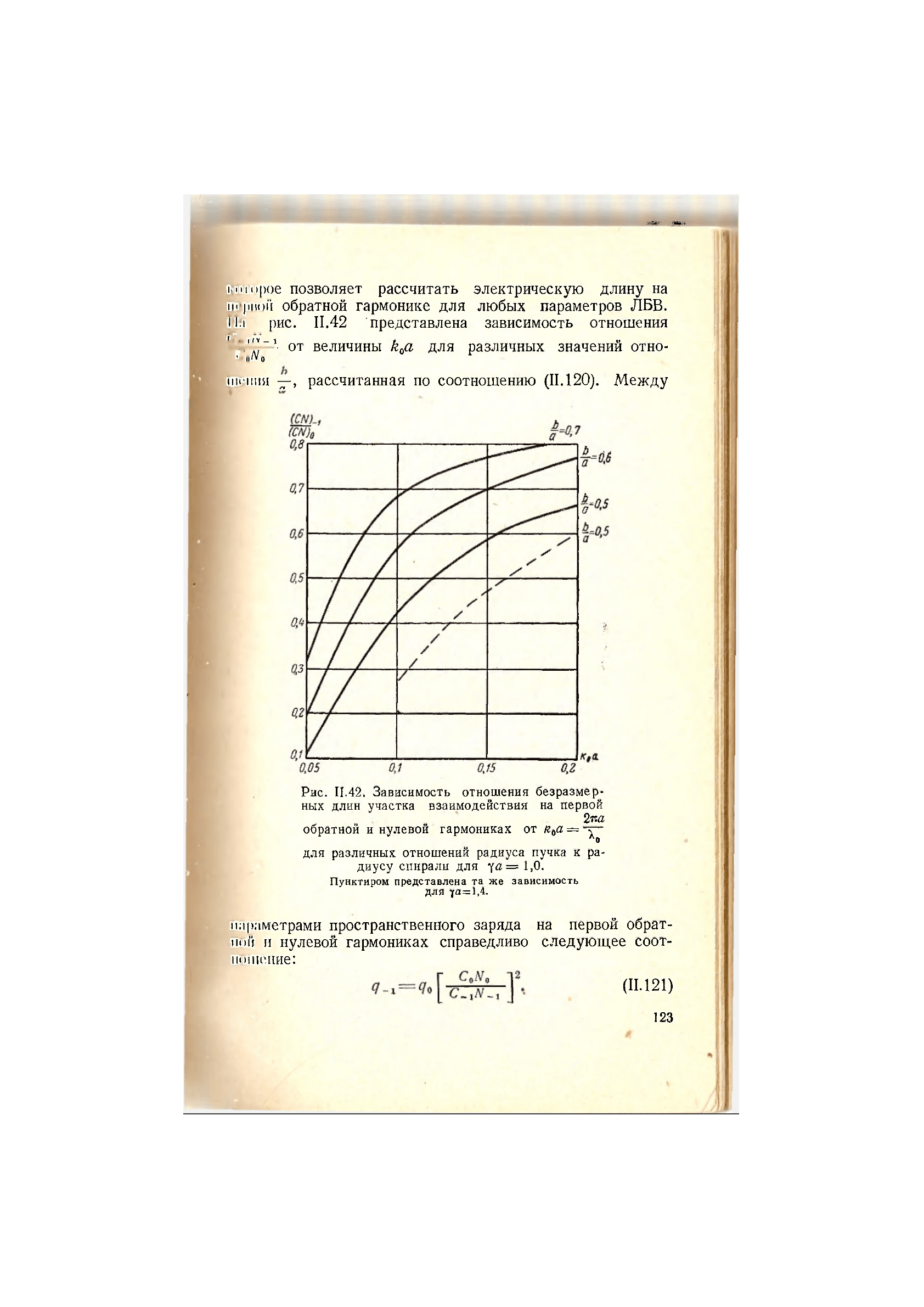
Ни рис. 11.42 представлена зависимость отношения

fcV""* от величины k

a для различных значений отно-

v о /V о

шеиия рассчитанная по соотношению (11.120). Между

Рис. 11.42. Зависимость отношения безразмер-

ных длин участка взаимодействия на первой

2 па

обратной и нулевой гармониках от я

а = -т—

для различных отношений радиуса пучка к ра-

диусу спирали для fa= 1,0.

Пунктиром представлена та же зависимость

для fa=l,4.

параметрами пространственного заряда

ной и нулевой гармониках справедливо

ношение:

на первой обрат-

следующее соот-

(11.121)

123

Так как отношение

л/

°— > 1, то параметр Прост-

ев

-\N -

ранственного заряда на первой обратной гармонике

больше параметра пространственного заряда на нулевой

гармонике. Если полученное значение C.jiV.j>(CiV)

cxl

рассчитанного для параметра пространственного заря-

да д_

, то возникает паразитная генерация. В работах

[25, 261 по соотношению, аналогичному выражению

(11.120), рассчитано отношение * и определена ма4

ксимальная электрическая длина ЛБВ на основной гар^

монике, при которой возбуждение на первой обратной

гармонике происходить не будет (при этом предполага-

лось, что затухание отсутствует). Анализ, проведенный

[25, 26], является недостаточным, так как следует так-j

же определить затухание, необходимое для стабильной

работы ЛБВ, если ее длина больше максимально допу-|

стимой (это иногда может иметь место).

Так как в ЛБВ обычно применяется локальный по-!

глотитель, то для этого необходимо определить пусковые

условия генератора обратной волны при наличии локаль-

ного затухания большой величины. Метод рядов, изло-<

женный выше, позволяет решить эту задачу. Результаты

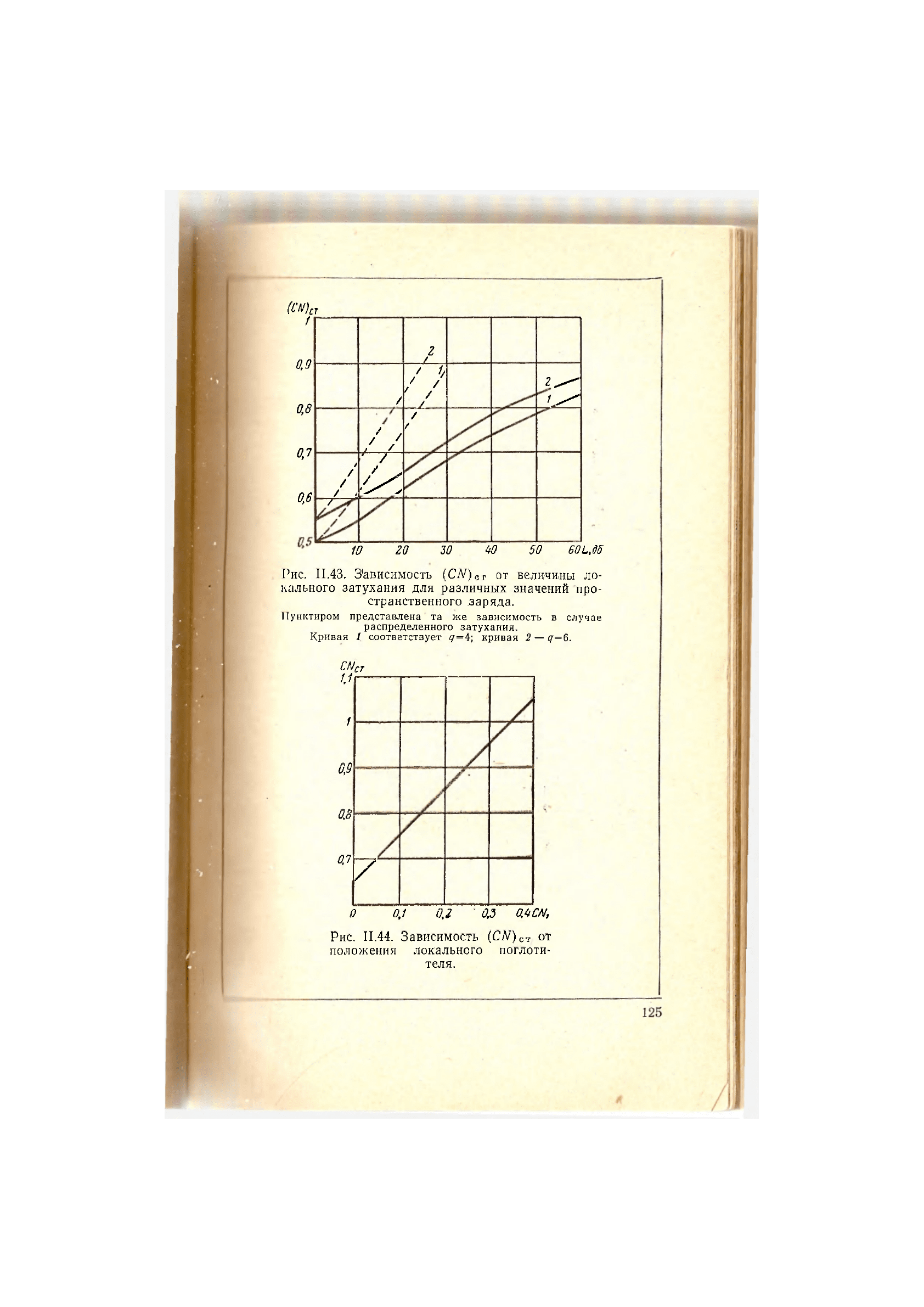
расчета представлены на рис. 11.43, где представлена за-

висимость величины (CN)

ст

от величины локального за--

тухания для двух значений параметра пространственно-

го заряда. При расчетах использовалась следующая

связь между параметрами затухания на первой обратной

и нулевой гармониках:

i —

o Со N

На рис. 11.44 показана зависимость величины (CAf)

от положения локального поглотителя. Полученные ре-

зультаты дают возможность определить величину ло-'j

кального затухания, необходимую для стабильной рабо-

ты ЛБВ, в зависимости от параметров прибора. На

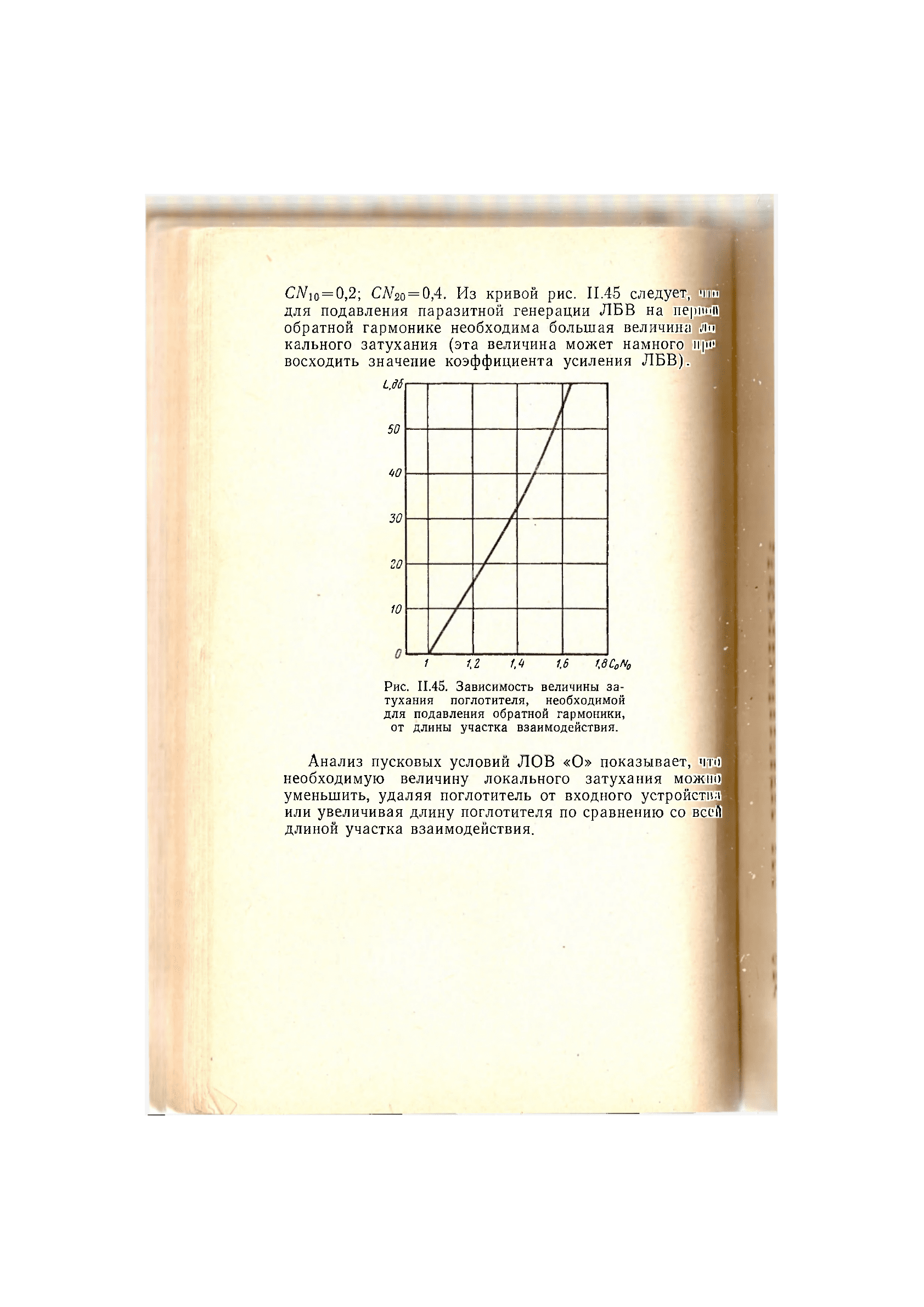
рис. 11.45 представлена зависимость величины ло-кально-j

го затухания, необходимого для подавления паразитной]

генерации ЛБВ на обратной гармонике, в зависимости

от параметра C

для значений —=0,5, k

a =

0,1

и для

Иг

Yofl —

1. 'При ЭТЙХ расчетах принято </о—1;

124

(СЮст

0,9

0,8

0,7

0,6

10 20 30 40 50 60L,d5

Рис. 11.43. Зависимость (CN)

от величины ло-

кального затухания для различных значений про-

странственного заряда.

Пунктиром представлена та же зависимость в случае

распределенного затухания.

Кривая 1. соответствует q=4; кривая 2 — q=6.

0,9

0,8

0,7

О 0,1 ОЛ 0,3 0,4 CN

Рис. 11.44. Зависимость (CN)

cт

. от

положения локального поглоти-

теля.

(

/ <!

/ .

/ У

' ^^ V

CjV

=0,2; CN

o=0,4. Из кривой рис. 11.45 следует, Mtfl

для подавления паразитной генерации ЛБВ на nepuu|

обратной гармонике необходима большая величина Щ

кального затухания (эта величина может намного iipfK

восходить значение коэффициента усиления ЛБВ|н

L,d6

1 1,2 1,4 1,6 UQC

Рис. 11.45. Зависимость величины за-

тухания поглотителя, необходимой

для подавления обратной гармоники,

от длины участка взаимодействия.

Анализ пусковых условий ЛОВ «О» показывает, что

необходимую величину локального затухания можно

уменьшить, удаляя поглотитель от входного устройств»

или увеличивая длину поглотителя по сравнению со всей

длиной участка взаимодействия.

ГЛАВА III

111"

ИI»Л И ЖЕ Н Н Ы Е МЕТОДЫ АНАЛИЗА РАБОТЫ

ЛАМПЫ БЕГУЩЕЙ ВОЛНЫ

III.1. ВВЕДЕНИЕ

Амйлиз, проведенный в предыдущей главе, показал,

М усиление ЛБВ является довольно сложной функцией

1|11М'й характеристического уравнения. Для нахождения

|1|мк<й в общем случае при наличии затухания и при

М'и.ших значениях параметра усиления следует решить

•имение четвертой степени с комплексными коэффи-

И^мIими. Это приводит к очень громоздким выкладкам

i< необходимости использования электронно-счетных

^Тройств. Поэтому наряду со строгим рассмотрением

Идл чп

о взаимодействии электронного потока с бегущей

Мной разработаны приближенные методы анализа, поз-

|Ш0Щие достаточно просто с тем или иным приближен

и|М рассчитать усиление ЛБВ. Мы не будем здесь рас-

Могривать приближенные математические методы, поз-

(МИЮЩие определить усиление через коэффициенты ха-

мим ристического уравнения, не решая самого уравне-

нн (один из этих методов рассмотрен в предыдущей

Л0по)•

И настоящее время наиболее широкое распростране-

нг из приближенных методов получили метод заданно-

0 ноля, приближенный энергетический метод и метод

им мсдовательных приближений.

III.2. МЕТОД ЗАДАННОГО ПОЛЯ

Метод заданного поля является наиболее простым

гочки зрения математического аппарата и поэтому поз-

влиет дать наглядную картину физических явлений.

Лггод заданного поля в применении к расчету усиления

.127

ЛБВ изложен в работах Лопухина, Коваленко [1], Ш||

чика [2] и Тагера.

При решении задачи о взаимодействии электрощит

потока с бегущей волной в ЛБВ в приближении зЬдлЯ

ного поля предполагают, что поле в линии может быщ

представлено одной волной с постоянной фазовой CKM

ростью, причем амплитуда напряженности электрически'

то поля изменяется вдоль линии по экспоненциальном®

закону.

Амплитудная постоянная распространения, а следе)!

вательно, и коэффициент усиления вычисляются из рйм

венства активных составляющих электронной мощности

и потока мощности в линии.

-Pea=~Y^ ^E(z).i*(z)dz = P

(III, I)

где

E(z)=E

-e ~

= £

(т

/р)

(1Щ

i(z)— конвекционный ток, возбуждаемый в пучке по*

лем E(z)\

— сопротивление связи;

8 = фазовая постоянная в системе с пучком;

— амплитудная постоянная, характеризующая yd;и|

ление.

При анализе предполагается, что потери в линии Дрм

небрежимо малы.

Введем параметр несинхронности для возмущенной

волны, определяемый по формуле

Тогда выражение для напряженности поля может]

быть записано следующим образом:

Е (г) Ц £

е*

(1+&

С) г

. (1П.2а)

Выражение для конвекционного тока можно полу-1

чить из дифференциального уравнения, выведенного,]

в первой главе (1.42):

.128

ч\ решение этого уравнения имеет вид

I (г =/

(х) ШЯж+

J [>qr

О -

(0) cos

^ - Щ (0)],

(III.5)

Ml' /(0) и v(0) —переменные составляющие тока и ско-

Rljt in о точке 2=0. Так как в ЛБВ обычно начальная мо-

|№Н1Ция отсутствует, то г*(0) =^(0) =0.

Подставляя в соотношение (III.5) значение Е(х) из

(III i) и интегрируя, получаем

•/ Щ* -toteE* е<Т-/*>* у

т—1

2Uo

• x[l — е™

(cos P,z + I^sinp^)], (III.6)

ъщще,

(Ш.7)

Миля конвекционный ток, можно определить актив-

Нут составляющую мощности взаимодействия электрон-

ами

о потока с полем бегущей волны:

I р

еа

= Re 1 [ ШШМ

\ (Y +№* + § ) Щ

• Х[е

(7+/

— cos^z — ^^sm^zjrfzl.

I In гсгрируя, получаем

__ /рДрРв

^-1) + 2|

[l—- e^ cos kl-

cos <yq-2nCN) — |

fi ,

k* j

Vq-2nCN J

ii 1230

129

Где

ШШ

TtCN = $

Cl; (III.H)

Допустим, что усиление велико, тогда е

>1. БэтоИ

случае

еа

IoE

+ b\Y + 2q (52 - b\) + q\

Приравнивая это выражение активной составляющей

ЕЬ^

потока мощности в линии: , получаем урав-

нение для определения амплитудной постоянной 8:

2Ь ' . ШЖ

(§2

ь\)

+ 2q

(52 _Щ +^2

—

(III. 9)

Наедем оптимальное значение параметра несин-

хронности для возмущенной волны, bi==b

0I£T

, при кото-'

ром усиление максимально. Для этого приравняем нулю

производную по b левой части выражения (III.9), в ре-

зультате получим

(С - ч) Щ£

• д+8&ОПХ

(С - q) -

Щ 0.

(III. 10)

Подставляя значение bi=b

из (III. 10) в (III.9),

найдем

= бмакс и коэффициент усиления:

макс

t = B

CN. (111.11)

Для пренебрежимо малого пространственного заряда

= 0 из (ШЛО) находим Ь

0пт

-^-

и соответственно

^макс 47,3. ^ч

В_случае большого пространственного заряда Ь

ШЬя

q, что дает

• Ямакс = 77,2 YVt+VW - Я• Щш

Этот же результат можно получить, если вместо

уравнения баланса активной мощности воспользоваться

130

Шнинием возбуждения линии, выведенным в первой

P«it« (1.39):

Н^ ^-г

^=_г

/с

ф), (ШЛЗ)

ЩР Г||-/РО — постоянная распространения волны в от-

II и

мне электронного потока.

Подставляя в это уравнение Е

из (111.2а) и i(z) из

(111(1) и сохраняя только члены, изменяющиеся с рас-

Шикнем по экспоненциальному закону, получаем

11риравнивая мнимые части и воспользовавшись (III.7),

(III Н), а также соотношениями J-г*

справедли-

вее Ре

}Мми для малых значений параметра усиления, получаем

урпнмеиие

26,

=][

IllMOpoe совпадает с (III.9).

II 1.3. ПРИБЛИЖЕННЫЙ ЭНЕРГЕТИЧЕСКИЙ МЕТОД

При решении задачи о взаимодействии электронного

Потока с электромагнитной волной в приближении за-

данного поля получается неплохое соответствие с резуль-

ими строгой теории для усиления в асимптотическом

режиме. Однако в таком приближении нельзя исследо-

ptnii поведение сигнала в начальном участке лампы,

честности, определить параметр начальных потерь.

Приближенный энергетический метод является даль-

нейшим обобщением метода заданного поля. Он состр-

MI н том, что закон изменения амплитуды £"1(2) напря*

Им*нкости ВЧ поля не задается заранее, а определяется

Н« уравнения баланса активной мощности, составленное

In для произвольной точки линии*. При этом, как и

И методе заданного поля, предполагается, что поле в ли-

нии, возникающее в результате взаимодействия волны

* Этот метод был впервые предложен 'В. Т. Овчаро-вьвм в 1947 г.

131

с пучком, может быть представлено одной волной с пи

стоянной фазовой скоростью.

Условие баланса активной мощности приводит к ни

тегральному уравнению, решение которого позволяв

найти распределение амплитуды напряженности ВЧ поД

вдоль линии. Это в свою очередь дает возможность риЫ

считать усиление ЛБВ с учетом начальных потерь, j

Предположим сначала, что линия не имеет потери!

Тогда уравнение баланса ВЧ мощности в любой точки

линии может быть записано в виде

EUZ) EUO) J

Pea (?) = Рл — Рвх = Чг-^

Т^

(ВД'

Kc 2f

Kc 1

где P

(z)=—2 Re J E(x)i*(x)dx. 1

Воспользовавшись формулой (III.5) для конв£кцион<]

ного тока при /(0)=а(0)=0, найдем выражение для ак«

тивной мощности взаимодействия

Щж

X [ Е(t)sin (х — t) еГ^

(Ш.15)|

Записывая выражение E{z) в виде

Е (z) = Е\ (г) е~

/рг

= E

(z)

{HblC) 2

(III. 16)

и воспользовавшись уравнением (III.14), получаем инте-

гральное уравнение для амплитуды поля Е\ (г):

Z X

J- J Е

рс) dx f Е

(it)

sin k{x — t) sin (x — t) dt= Щ

о 0

2m 2m ' Pill

где m = №

. . (111.18)

132