Celletti A. Stability and Chaos in Celestial Mechanics
Подождите немного. Документ загружается.

64 4 The three–body problem and the Lagrangian solutions
restricted three–body problem. In an inertial reference frame whose origin coincides
with the barycenter of the three bodies, let ξ
1
, ξ
2
, ξ
3
∈ R
2
be the corresponding
coordinates. From Newton’s gravitational law one obtains that the motion of P
1
and P
2
is described by the equations
d
2
ξ
1
dt
2
= G
m
2
(ξ
2
− ξ
1
)
|ξ
2
− ξ
1
|
3
+ G
m
3
(ξ
3
− ξ
1
)
|ξ
3
− ξ
1
|
3
,
d
2
ξ
2
dt
2
= −G
m
1
(ξ
2
− ξ
1
)
|ξ
2
− ξ
1
|
3
−G
m
3
(ξ
2
− ξ
3
)
|ξ
2
− ξ
3
|
3
.
Next we consider a (heliocentric) reference frame with origin coinciding with P
1
;
let r
2
≡ ξ
2
− ξ
1
, r
3
≡ ξ
3
− ξ
1
be the relative positions with ρ
2
≡|r
2
|, ρ
3
≡|r
3
|.
Then, one obtains
d
2
r
2
dt
2
= −
G(m
1
+ m
2
)r
2
ρ
3
2
−
Gm
3
r
3
ρ
3
3
+
Gm
3
(r
3
− r
2
)
|r
3
− r
2
|
3
.
Setting μ ≡G(m
1
+ m
2
)andε = Gm
3
, one has
d
2
r
2
dt
2
+
μr
2
ρ
3
2
= −ε
∂R
∂r
2
,
where the function R takes the form
R =
r
2
· r
3
ρ
3
3
−
1
|r
3
− r
2
|
. (4.1)
Notice that for ε = 0 the dynamics reduces to the two–body problem of the motion
of P
2
around P
1
. For this reason we shall refer to ε as the perturbing parameter
and to R as the perturbing function of the Keplerian motion. Recalling (3.36) we
can write the three–body Hamiltonian as
H
0
(L
0
,G
0
,
0
,g
0
)=−
μ
2
2L
2
0
+ εR(L
0
,G
0
,
0
,g
0
) , (4.2)
where R is given by (4.1) and the functions r
2
, r
3
must be expressed in terms
of the Delaunay variables. Since the motion of P
3
around P
1
is circular, normal-
izing the time so that the angular velocity of P
3
is equal to one, one obtains
r
3
=(ρ
3
cos t, ρ
3
sin t). Denoting by ϑ the longitude of P
2
and using r
2
· r
3
=
ρ
2
ρ
3
cos(ϑ − t), one obtains |r
3
− r
2
| =
ρ
2
2
+ ρ
2
3
− 2ρ
2
ρ
3
cos(ϑ − t). As a conse-
quence, the perturbing function takes the form
R =
ρ
2
cos(ϑ − t)
ρ
2
3
−
1
ρ
2
2
+ ρ
2
3
− 2ρ
2
ρ
3
cos(ϑ − t)
. (4.3)
We immediately remark that R depends upon the difference ϑ − t;beingϑ =
g
0
+ f, one obtains that R depends on the difference g
0
−t. Therefore we perform

4.1 The restricted three–body problem 65
the canonical change of variables from the Delaunay coordinates (L
0
,G
0
,
0
,g
0
)
introduced in Chapter 3 to a new set of variables (L, G, , g) defined as
=
0
,L= L
0
,
g = g
0
− t, G= G
0
.
The transformed Hamiltonian takes the form
H(L, G, , g)=−
μ
2
2L
2
− G
+ ε
ρ
2
cos(g + f )
ρ
2
3
−
ε
ρ
2
2
+ ρ
2
3
− 2ρ
2
ρ
3
cos(g + f )
,
where ρ
2
, f are intended to be expressed in terms of the mean anomaly.
4.1.2 Expansion of the perturbing function
The perturbing function (4.3) can be written in terms of the Delaunay variables.
Here we compute explicitly the first few coefficients of its Fourier–Taylor series
expansion and we refer to Appendix C (see also [61, 67, 68]) for general formulae
valid at any order.
Let us introduce the Legendre polynomials P
j
(x) defined through the recursive
relations
P
0
(x)=1
P
1
(x)=x
P
j+1
(x)=
(2j +1)P
j
(x)x − jP
j−1
(x)
j +1
for any j ≥ 1 .
Apart from a constant factor, the second term in (4.3) becomes
1
ρ
2
2
+ ρ
2
3
− 2ρ
2
ρ
3
cos(ϑ − t)
=
1
ρ
3
∞
j=0
P
j
(cos(ϑ − t))
ρ
2
ρ
3
j
,
from which we obtain
R = −
1
ρ
3
∞
j=2
P
j
(cos(ϑ − t))
ρ
2
ρ
3
j
. (4.4)
The inversion of Kepler’s equation (3.24) up to the second order in the eccentricity
yields
u = +esin +
e
2
2
sin(2)+O(e
3
) .
Using (3.23) one obtains
f = +2esin +
5
4
e
2
sin 2l + O(e
3
) ,
66 4 The three–body problem and the Lagrangian solutions
so that
ϑ − t = g + +2esin +
5
4
e
2
sin 2 + O(e
3
) . (4.5)
In a similar way, from ρ
2
= a(1 − ecosu)oneobtains:
ρ
2
= a
1+
1
2
e
2
− ecos −
1
2
e
2
cos 2
+ O(e
3
) . (4.6)
Recall that the ecccentricity is a function of the Delaunay variables through the
relation e =
1 −
G
2
L
2
.Thepowers(
ρ
2
a
)
j
for j =2, 3,... admit the following
expansions:
ρ
2
a
2
=1+
3
2
e
2
− 2e cos −
1
2
e
2
cos 2 + O(e
3
)
ρ
2
a
3
=1+3e
2
− 3e cos + O(e
3
)
ρ
2
a
4
=1+5e
2
− 4e cos +e
2
cos 2 + O(e
3
)
ρ
2
a
5
=1− 5e cos +e
2
15
2
+
5
2
cos 2
+ O(e
3
) ... .
From (4.4), one gets:
R = −
1
ρ
3
[P
2
(cos(ϑ − t)) (
ρ
2
a
)
2
(
a
ρ
3
)
2
+ P
3
(cos(ϑ − t)) (
ρ
2
a
)
3
(
a
ρ
3
)
3
+P
4
(cos(ϑ − t)) (
ρ
2
a
)
4
(
a
ρ
3
)
4
+ P
5
(cos(ϑ − t)) (
ρ
2
a
)
5
(
a
ρ
3
)
5
]+... .
Casting together (4.5), (4.6) and normalizing the unit of length so that ρ
3
=1,one
obtains the expansion
R = R
00
(L, G)+R
10
(L, G)cos + R
11
(L, G) cos( + g)
+ R
12
(L, G) cos( +2g)+R
22
(L, G)cos(2 +2g)
+ R
32
(L, G)cos(3 +2g)+R
33
(L, G)cos(3 +3g)
+ R
44
(L, G)cos(4 +4g)+R
55
(L, G)cos(5 +5g)+... , (4.7)
where the coefficients R
ij
are given by the following expressions:
R
00
= −
L
4
4
1+
9
16
L
4
+
3
2
e
2
+ ... , R
10
=
L
4
e
2
1+
9
8
L
4
+ ...
R
11
= −
3
8
L
6
1+
5
8
L
4
+ ... , R
12
=
L
4
e
4
(9 + 5L
4
)+...
R
22
= −
L
4
4
3+
5
4
L
4
+ ... , R
32
= −
3
4
L
4
e+...
R
33
= −
5
8
L
6
1+
7
16
L
4
+ ... , R
44
= −
35
64
L
8
+ ...
R
55
= −
63
128
L
10
+ ... (4.8)

4.1 The restricted three–body problem 67
4.1.3 The planar, elliptic, restricted three–body problem
If we assume that P
3
orbits around P
1
on an elliptic orbit with eccentricity e
,the
corresponding motion is described by a Hamiltonian function with three degrees of
freedom; if ψ denotes the longitude of P
3
and Ψ is the conjugated action variable,
the Hamiltonian of the elliptic case is given by
H(L, G, Ψ,,g,ψ)=−
1
2L
2
+Ψ+εR(L, G, , g, ψ;e
) ,
where R(L, G, , g, ψ;e
) depends parametrically on e
and, in normalized units, ε
is the primaries mass–ratio. Up to constants, the first few Fourier coefficients of
the series expansion of the perturbing function are the following:
R(L, G, , g, ψ)=
= −
L
4
4
5
2
+
9
16
L
4
−
3
2
G
2
L
2
+
3
2
e
2
+ L
4
e
2
1+
9
8
L
4
cos()
−
3
8
L
6
1+
5
8
L
4
cos( + g −ψ)+
L
4
4
e(9 + 5L
4
) cos( +2g − 2ψ)
−
L
4
4
3+
5
4
L
4
cos(2 +2g − 2ψ) −
3
4
L
4
ecos(3 +2g − 2ψ)
−
5
8
L
6
1+
7
16
L
4
cos(3 +3g − 3ψ) −
35
64
L
8
cos(4 +4g − 4ψ)
−
63
128
L
10
cos(5 +5g − 5ψ) −L
4
3
4
e
+
45
64
L
4
e
cos(ψ)
−L
4
21
8
e
+
45
32
e
L
4
cos(2 +2g − 3ψ)
−L
4
−
3
8
e
+
5
32
e
L
4
cos(2 +2g − ψ)+...
4.1.4 The inclined, circular, restricted three–body problem
We assume that the motion of P
3
around P
1
is circular, but we let the planes of
the orbits of P
2
and P
3
have a non–zero mutual inclination i. Using the spatial
Delaunay variables (L, G, H, , g, h) introduced in Chapter 3, denoting with ψ the
longitude of P
3
, the Hamiltonian function takes the form:
H(L, G, H, , g, h, ψ)=−
1
2L
2
− H + εR(L, G, H, , g, h, ψ) ,
where, setting γ =
1
2
−
H
2G
, up to constants the first few terms of the Fourier
expansion of the perturbing function are given by

68 4 The three–body problem and the Lagrangian solutions
R(L, G, H, , g, h, ψ)=−L
4
1
4
+
3
8
e
2
+
9
64
L
4
−
3
2
γ
2
−
3
4
−
3
2
γ
2
+
5
16
L
4
cos(2 +2g +2h − 2ψ)
−
−
1
2
e+3γ
2
e −
9
16
eL
4
cos() −
3
4
e −
3
2
γ
2
e
cos(3 +2g +2h − 2ψ)
−
−
9
4
e+
9
2
γ
2
e −
5
4
eL
4
cos( +2g +2h − 2ψ) −
3
2
γ
2
cos(2 +2g)
−
3
2
γ
2
cos(2h − 2ψ) −
3
2
γ
2
ecos(3 +2g)
+
9
2
γ
2
e cos( +2g)+
3
2
γ
2
e cos( +2h − 2ψ)
+
3
2
γ
2
e cos( − 2h +2ψ) − L
6
3
8
+
15
64
L
4
cos( + g + h − ψ)
−
5
8
+
35
128
L
4
L
6
cos(3 +3g +3h − 3ψ)
−
35
64
L
8
cos(4 +4g +4h − 4ψ) −
63
128
L
10
cos(5 +5g +5h − 5ψ)+...
4.2 The circular, restricted Lagrangian solutions
In the framework of the restricted, planar, circular three–body problem, Euler
and Lagrange proved that in a rotating reference frame the equations of motion
admit the existence of equilibrium solutions, known as the collinear and triangular
equilibrium points. A concrete example is provided by the Trojan and Greek groups
of asteroids, which (approximately) form an equilateral triangle with Jupiter and
the Sun.
The mathematical derivation of such equilibrium solutions is the following. Con-
sider a sidereal reference frame (O,ξ,η,ζ), where O coincides with the barycenter
of the three bodies, the ξ axis lies along the direction joining the bodies with masses
m
1
and m
3
at time t =0,η is orthogonal to ξ and belongs to the orbital plane,
while ζ is perpendicular to the orbital plane. Let (ξ
i
,η
i
,ζ
i
), i =1, 3, be the coordi-
nates of the primaries P
1
and P
3
. We normalize the units of measure so that the
distance between the primaries is unity and that G(m
1
+ m
3
) = 1. Without loss of
generality we assume that m
1
>m
3
and let
μ ≡
m
3
m
1
+ m
3
,
so that μ
1
≡Gm
1
=1− μ, μ
3
≡Gm
3
= μ. The equations of motion of P
2
with
coordinates (ξ,η,ζ) can be written as
4.2 The circular, restricted Lagrangian solutions 69
¨
ξ = μ
1
ξ
1
− ξ
r
3
1
+ μ
3
ξ
3
− ξ
r
3
3
¨η = μ
1
η
1
− η
r
3
1
+ μ
3
η
3
− η
r
3
3
¨
ζ = μ
1
ζ
1
− ζ
r
3
1
+ μ
3
ζ
3
− ζ
r
3
3
, (4.9)
where r
1
and r
3
denote the distances from the primaries:
r
1
=
(ξ
1
− ξ)
2
+(η
1
− η)
2
+(ζ
1
− ζ)
2
,
r
3
=
(ξ
3
− ξ)
2
+(η
3
− η)
2
+(ζ
3
− ζ)
2
.
Let us introduce a synodic reference frame (O,x,y,z), rotating with the angular
velocity n of the primaries, where n has been normalized to one, due to the choice
of the units of measure. Let us fix the axes so that the coordinates of the primaries
become (x
1
,y
1
,z
1
)=(−μ
3
, 0, 0), (x
3
,y
3
,z
3
)=(μ
1
, 0, 0). The link between the
synodic and the sidereal reference frames is
ξ = cos(t)x − sin(t)y
η =sin(t)x + cos(t)y
ζ = z, (4.10)
while the distances of P
2
from the primaries are now given by
r
1
=
(x + μ
3
)
2
+ y
2
+ z
2
,r
3
=
(x − μ
1
)
2
+ y
2
+ z
2
. (4.11)
Computing the second derivative of (4.10) with respect to time and inserting the
result in (4.9) one obtains the equations of motion in the synodic frame:
¨x − 2˙y =
∂U
∂x
¨y +2˙x =
∂U
∂y
¨z =
∂U
∂z
, (4.12)
where the function U is defined as
U = U (x, y, z) ≡
1
2
(x
2
+ y
2
)+
μ
1
r
1
+
μ
3
r
3
. (4.13)
Multiplying (4.12) by ˙x,˙y,˙z and adding the results, one obtains:
˙x¨x +˙y¨y +˙z¨z =
∂U
∂x
˙x +
∂U
∂y
˙y +
∂U
∂z
˙z ; (4.14)
notice that the left–hand side of (4.14) is equal to
1
2
d
dt
(˙x
2
+˙y
2
+˙z
2
), while the
right–hand side is equal to
dU
dt
. Therefore, integrating with respect to time one gets
˙x
2
+˙y
2
+˙z
2
=2U − C
J
, (4.15)

70 4 The three–body problem and the Lagrangian solutions
where C
J
is a constant of integration, called the Jacobi integral. Using (4.13) one
obtains
C
J
= x
2
+ y
2
+2
μ
1
r
1
+2
μ
3
r
3
− (˙x
2
+˙y
2
+˙z
2
) . (4.16)
Notice that (4.15) implies 2U − C
J
≥ 0. The curves of zero velocity are defined
through the expression C
J
=2U ; such a relation defines a boundary, called Hill’s
surface, which separates regions where motion is allowed or forbidden. An example
of Hill’s region is given in Figure 4.1.
Fig. 4.1. The triangular and collinear equilibrium points with an example of Hill’s sur-
faces.
Let us now turn to the determination of the position of the equilibrium points
in the planar case with z = 0 [142], since we assumed that the motion of the three
bodies takes place on the same plane. Recalling (4.11) and using μ
1
+ μ
3
= 1 one
has:
μ
1
r
2
1
+ μ
3
r
2
3
= x
2
+ y
2
+ μ
1
μ
3
.
Inserting such an expression in U one has
U = μ
1
r
2
1
2
+
1
r
1
+ μ
3
r
2
3
2
+
1
r
3
−
1
2
μ
1
μ
3
.
The equilibrium points are the solutions of the system obtained imposing that the
partial derivatives of (4.13) with respect to x and y are zero:
∂U
∂x
=
∂U
∂r
1
∂r
1
∂x
+
∂U
∂r
3
∂r
3
∂x
= μ
1
r
1
−
1
r
2
1
x + μ
3
r
1
+ μ
3
r
3
−
1
r
2
3
x − μ
1
r
3
=0
∂U
∂y
=
∂U
∂r
1
∂r
1
∂y
+
∂U
∂r
3
∂r
3
∂y
= μ
1
r
1
−
1
r
2
1
y
r
1
+ μ
3
r
3
−
1
r
2
3
y
r
3
=0. (4.17)

4.2 The circular, restricted Lagrangian solutions 71
A solution of (4.17) is obtained by solving the equations
r
1
−
1
r
2
1
=0,r
3
−
1
r
2
3
=0,
from which one obtains r
1
= r
3
= 1, namely
(x + μ
3
)
2
+ y
2
=1, (x − μ
1
)
2
+ y
2
=1.
Solving these equations, one finds the equilibrium solutions
1
2
− μ
3
,
√
3
2
,
1
2
− μ
3
, −
√
3
2
,
whichcorrespondtothetriangular Lagrangian solutions, usually denoted as L
4
and L
5
(see Figure 4.1).
Other solutions are obtained observing that y = 0 solves the second of (4.17);
in particular, there exist three col linear equilibrium solutions usually denoted as
L
1
, L
2
, L
3
,whereL
1
is located between the primaries, while L
2
and L
3
are outside
the primaries. We derive in detail the location of L
1
; the same procedure can be
straightforwardly extended to L
2
and L
3
.
At L
1
we have y = 0 and r
1
= x + μ
3
, r
3
= −x + μ
1
,sothatr
1
+ r
3
=1;
moreover,
∂r
1
∂x
= −
∂r
3
∂x
= 1. Replacing in
∂U
∂x
= 0, one obtains
μ
1
1 − r
3
−
1
(1 − r
3
)
2
− μ
3
r
3
−
1
r
2
3
=0,
from which one gets
μ
3
3μ
1
= r
3
3
1 − r
3
+
r
2
3
3
(1 + r
3
+ r
2
3
)(1 − r
3
)
3
.
Define α ≡ (
μ
3
3μ
1
)
1/3
; developing α in Taylor series, one finds
α = r
3
+
1
3
r
2
3
+
1
3
r
3
3
+
53
81
r
4
3
+ ...
Inverting such relation, for example using the Lagrange inversion method [142], one
has
r
3
= α −
1
3
α
2
−
1
9
α
3
−
23
81
α
4
+ ... (4.18)
Since r
3
represents the distance along the x–axis from the body with mass m
3
,the
solution (4.18) provides the location of the equilibrium point L
1
as a function of the
mass ratio α. Similar computations can be performed for L
2
such that r
1
= x + μ
3
and r
3
= x−μ
1
with r
1
−r
3
= 1, and for L
3
such that r
1
= −x−μ
3
and r
3
= −x+μ
1
with r
3
− r
1
=1.
To give a concrete example, in the Moon–Earth system the location of the
equilibrium points is the following: L
1
lies at 3.26 · 10
5
km from the Earth, L
2
is
72 4 The three–body problem and the Lagrangian solutions
at 4.49 ·10
5
km, L
3
is about 3.82 ·10
5
km from the Earth, while L
4
and L
5
are the
triangular positions at 3.84 · 10
5
km, being located on the Moon’s orbit.
We conclude with a discussion on the linear stability of the equilibrium positions
(see [142]). Let us denote by (x
,y
) one of the five stationary solutions (L
1
,...,L
5
);
let (δ
x
,δ
y
) be a small displacement from the equilibrium and let (x, y) ≡ (x
+
δ
x
,y
+ δ
y
). Let us insert such coordinates in (4.12) and expand the derivatives of
U in a neighborhood of the equilibrium solution. Using the notation
U
xx
=
∂
2
U(x
,y
)
∂x
2
,U
xy
=
∂
2
U(x
,y
)
∂x∂y
,U
yy
=
∂
2
U(x
,y
)
∂y
2
,
the equations for the variations (δ
x
,δ
y
) can be written as
⎛
⎜
⎜
⎝
˙
δ
x
˙
δ
y
¨
δ
x
¨
δ
y
⎞
⎟
⎟
⎠
= A
⎛
⎜
⎜
⎝
δ
x
δ
y
˙
δ
x
˙
δ
y
⎞
⎟
⎟
⎠
,
where
A ≡
⎛
⎜
⎜
⎝
0010
0001
U
xx
U
xy
02
U
xy
U
yy
−20
⎞
⎟
⎟
⎠
.
The eigenvalues of A are the solutions of the secular equation det(A − λI
4
)=0
(where I
4
is the 4 × 4 identity matrix), namely
λ
4
+(4− U
xx
− U
yy
)λ
2
+(U
xx
U
yy
− U
2
xy
)=0.
This equation admits four roots:
λ
1,2
= ±
1
2
(U
xx
+ U
yy
− 4) −
1
2
[(4 − U
xx
− U
yy
)
2
− 4(U
xx
U
yy
− U
2
xy
)]
1
2
1
2
λ
3,4
= ±
1
2
(U
xx
+ U
yy
− 4) +
1
2
[(4 − U
xx
− U
yy
)
2
− 4(U
xx
U
yy
− U
2
xy
)]
1
2
1
2
.
The equilibrium solution is stable, if the eigenvalues are purely imaginary.
For the collinear equilibrium position L
1
, one has y
=0,r
1
= x
+ μ
3
,
r
3
= −x
+ μ
1
; defining M ≡
μ
1
r
3
1
+
μ
3
r
3
3
, the characteristic equation becomes
λ
4
+(2− M)λ
2
+(1+M − 2M
2
)=0.
Therefore the product of the four eigenvalues amounts to 1 + M − 2M
2
,withthe
constraints λ
1
= −λ
2
, λ
3
= −λ
4
. The eigenvalues are purely imaginary provided
that λ
2
1
= λ
2
2
< 0andλ
2
3
= λ
2
4
< 0, which imply that 1 + M − 2M
2
> 0, namely
−
1
2
<M<1. These inequalities would guarantee the stability of the equilibrium
point; however, computing M at the collinear point L
1
one finds that M>1. In
fact, in the case of L
1
we know that r
1
< 1andr
3
< 1, so that M>μ
1
+ μ
3
=1.
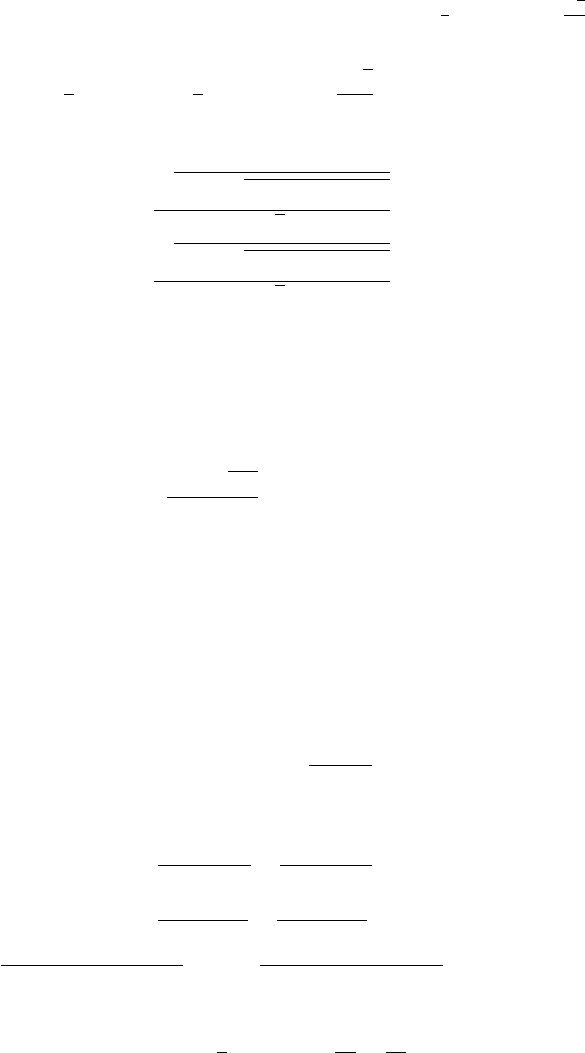
4.3 The elliptic, restricted Lagrangian solutions 73
We conclude that the collinear point L
1
is unstable for any value of the masses.
The same conclusion holds for L
2
and L
3
.
Concerning the triangular equilibrium positions one has x
=
1
2
−μ
3
, y
= ±
√
3
2
,
r
1
= r
3
= 1. Computing the derivatives of U at the equilibria, one obtains
U
xx
=
3
4
,U
yy
=
9
4
,U
xy
= ±
3
√
3
4
(1 − 2μ
3
) .
The eigenvalues become
λ
1,2
= ±
−1 −
1 − 27(1 − μ
3
)μ
3
√
2
,
λ
3,4
= ±
−1+
1 − 27(1 − μ
3
)μ
3
√
2
.
The eigenvalues are purely imaginary provided
1 − 27(1 − μ
3
)μ
3
≥ 0 ; (4.19)
recalling that we assumed m
1
>m
3
,sothatμ
1
>μ
3
with μ
1
+ μ
3
= 1, taking into
account the inequality (4.19) one obtains
μ
3
≤
27 −
√
621
54
0.0385 . (4.20)
In conclusion, if the masses verify (4.20), then the triangular equilibrium solutions
are linearly stable.
4.3 The elliptic, restricted Lagrangian solutions
Consider the planar motion of a body P
2
(x, y) of mass μ
2
in the gravitational field of
two primaries, P
1
(x
1
,y
1
)andP
3
(x
3
,y
3
) with masses μ
1
and μ
3
, which are assumed
to move on elliptic orbits around their common center of mass O;letf denote the
true anomaly of the common ellipse and let r =
a(1−e
2
)
1+e cos f
be the distance between
P
1
and P
3
. In an inertial barycentric reference frame, the cartesian equations of
the motion of P
2
are given by
¨x = −
μ
1
(x − x
1
)
r
3
1
−
μ
3
(x − x
3
)
r
3
3
¨y = −
μ
1
(y − y
1
)
r
3
1
−
μ
3
(y − y
3
)
r
3
3
,
where r
1
=
(x − x
1
)
2
+(y − y
1
)
2
, r
3
=
(x − x
3
)
2
+(y − y
3
)
2
; the above equa-
tions are associated to the Lagrangian function
L(˙x, ˙y, x,y, r, f)=
1
2
(˙x
2
+˙y
2
)+
μ
1
r
1
+
μ
3
r
3
,
