Celletti A. Stability and Chaos in Celestial Mechanics
Подождите немного. Документ загружается.

94 5 Rotational dynamics
Considering the series expansion (5.18) up to the order 4 in the eccentricity,
one obtains
¨x + ε
e
4
24
sin(2x +2t)+
e
3
48
sin(2x + t)+
−
e
2
+
e
3
16
sin(2x − t)+
+
1 −
5
2
e
2
+
13
16
e
4
sin(2x − 2t)+
7
2
e −
123
16
e
3
sin(2x − 3t)+
+
17
2
e
2
−
115
6
e
4
sin(2x − 4t)+
845
48
e
3
sin(2x − 5t)+
+
533
16
e
4
sin(2x − 6t)
=0, (5.19)
which can be written in the form
¨x + εV (x, t)=0,
for a suitable periodic function V = V (x, t). Such an equation corresponds to that
of a pendulum subject to a forcing term, depending periodically upon the time.
5.5.2 The averaged equation
For a given resonance of order p : 2, let us define the resonant angle γ ≡ x −
p
2
t;in
terms of γ equation (5.18) becomes
¨γ + εW
p
2
, e
sin 2γ + ε
+∞
m=0,p, m=−∞
W
m
2
, e
sin(2γ +(p − m)t)=0.
Averaging over the time one obtains the pendulum equation
¨γ + εW
p
2
, e
sin 2γ =0,
which admits the energy integral
1
2
˙γ
2
−
ε
2
W
p
2
, e
cos 2γ = E,
being E the total mechanical energy. The equilibrium points correspond to γ =0
and γ =
π
2
(modulus π). If W (
p
2
, e) > 0thenγ = 0 is stable, while γ =
π
2
is unstable.
The maximum width η
p
(e) of the resonant region around the stable point amounts
to η
p
(e) ≡ 2
εW (
p
2
, e). For example, taking into account the expressions provided
in Table 5.1, one has
η
2
(0.0549) = 0.037 ,η
3
(0.0549) = 0.016 ,
η
2
(0.2056) = 0.023 ,η
3
(0.2056) = 0.020 ,
where p = 2 corresponds to the 1:1 resonance, p = 3 to the 3:2 resonance, e = 0.0549
is the eccentricity of the Moon and e = 0.2056 is that of Mercury; we have assumed
ε =3.45 · 10
−4
for the Moon and ε =1.5 · 10
−4
for Mercury (see also [33]).

5.5 The spin–orbit problem 95
5.5.3 The dissipative spin–orbit problem
In writing equation (5.16) we have explicitly neglected the dissipative effects; among
these terms, the most important contribution is typically due to the internal non–
rigidity of the body and it can be described by a model of tidal torque [78,79,123,
147]). Within the different expressions existing in the literature, we quote a tidal
torque depending linearly on the relative angular velocity as [147]
T (˙x; t)=−K
d
L(e,t)˙x − N(e,t)
,
where
L(e,t)=
a
6
r
6
,N(e,t)=
a
6
r
6
˙
f.
Moreover, the coefficient K
d
is named the dissipative constant; it depends on the
physical and orbital features of the body. More precisely, K
d
takes the form
K
d
≡ 3n
k
2
ξQ
R
e
a
3
M
m
,
where n is the mean motion, k
2
is the Love number (depending on the structure
of the body), Q is the so–called quality factor (which compares the frequency of
oscillation of the system to the rate of dissipation of energy), ξ is a structure
constant such that I
3
= ξmR
2
e
and, as before, R
e
is the equatorial radius, M is
themassofthecentralbodyP, m isthemassofS. Astronomical observations
suggest that for bodies like the Moon or Mercury the dissipative constant K
d
is of
the order of 10
−8
.
The expression for the tidal torque can be simplified by assuming (as in [50])
that the dynamics is essentially ruled by the averages of L(e,t)andN(e,t)over
one orbital period:
¯
T≡
¯
T (˙x)=−K
d
¯
L(e) ˙x −
¯
N(e)
(5.20)
where (compare with [147])
¯
L(e) ≡
1
(1 − e
2
)
9/2
1+3e
2
+
3
8
e
4
¯
N(e) ≡
1
(1 − e
2
)
6
1+
15
2
e
2
+
45
8
e
4
+
5
16
e
6
.
Thus, we are led to consider the following equation of motion for the dissipative
spin–orbit problem:
¨x + ε
a
r
3
sin(2x − 2f)=−K
d
¯
L(e) ˙x −
¯
N(e)
. (5.21)
Due to (5.20) the tidal torque vanishes provided
˙x ≡
¯
N(e)
¯
L(e)
=
1+
15
2
e
2
+
45
8
e
4
+
5
16
e
6
(1 − e
2
)
3
2
(1 + 3e
2
+
3
8
e
4
)
.

96 5 Rotational dynamics
It is readily shown that for circular orbits the angular velocity of rotation cor-
responds to the synchronous resonance, being ˙x = 1. For Mercury’s eccentricity
e=0.2056, it turns out that ˙x =1.256. We refer the reader to [9, 97, 144] for a
discussion on the problem of the capture into resonance under the effect of the
dissipation.
5.5.4 The discrete spin–orbit problem
Let us introduce the resonant angle of order p : 2 defined by the relation γ ≡ x−
p
2
t;
averaging also the conservative contribution over one orbital period, up to constants
one obtains
¨γ + εW
p
2
, e
sin 2γ = −K
d
¯
L(e) ˙γ −
¯
N(e)
,
which can be written as
˙γ =Γ
˙
Γ=−εW
p
2
, e
sin 2γ − K
d
¯
L(e)Γ −
¯
N(e)
. (5.22)
Integrating (5.22) through Euler’s symplectic method, one obtains
Γ
=Γ+h
− εW
p
2
, e
sin 2γ − K
d
¯
L(e)Γ −
¯
N(e)
γ
= γ + hΓ
t
= t + h, (5.23)
where h denotes the integration step and (Γ
,γ
) is the solution at time t + h.Let
us write (5.23) as
Γ
=
1 − hK
d
¯
L(e)
Γ+hK
d
¯
N(e) − hεW
p
2
, e
sin 2γ
γ
= γ + hΓ
t
= t + h ; (5.24)
notice that the determinant of the Jacobian of (5.24) is equal to 1 −hK
d
¯
L(e). The
quantity 1 −hK
d
¯
L(e) is positive for typical values of the parameters; for example,
if h =2π and K
d
=10
−3
, then the Jacobian is positive for any value of the
eccentricity less than 0.767.
In (5.24) take the integration step as h =2π and define b ≡ 1 − 2πK
d
¯
L(e),
c
0
≡ 2πK
d
¯
N(e), g(γ) ≡−2πW(
p
2
, e) sin 2γ. Then, considering the first two equa-
tions of (5.24) one obtains the following map at times 2π:
Γ
= bΓ+c
0
+ εg(γ)
γ
= γ +2πΓ
.
Performing the change of variables ξ = γ, η =2πΓ, we obtain the dissipative
standard map (see Section 1.7):
5.6 Motion around an oblate primary 97
η
= bη + c + εf (ξ)
ξ
= ξ + η
,
where c ≡ 2πc
0
and f(ξ)=2πg(ξ).
Remarks.
(a) Notice that the parameter c depends on
¯
N(e), which represents the average over
an orbital period of
a
6
r
6
˙
f. Therefore
¯
N(e) is zero whenever
˙
f =0,namelywhenthe
true anomaly is constant.
(b) Let us focus on the case when the dissipation is zero, namely
¯
L(e)Γ −
¯
N(e) = 0.
As far as Γ = 1 (corresponding to the synchronous resonance) one has that
¯
L(e) −
¯
N(e) = 0, which is satisfied only if e = 0; for Γ = 1.5 (corresponding to the 3:2
resonance) one has 1.5
¯
L(e) −
¯
N(e) = 0 which admits the solution e = 0.285.
5.6 Motion around an oblate primary
Let P be a body of finite dimensions with principal moments of inertia I
1
, I
2
,
I
3
and let S be a point–mass satellite orbiting under the gravitational influence
of P. The potential of this model is the same as in (5.10), (5.11) and therefore
we just limit ourselves to quoting the main formulae, which allow us to write the
equations of motion. Let M and m be the masses of P and S, respectively. Denote
by (O,x,y,z) a reference frame with origin in the center of mass O of P;letQ be a
generic point of P with coordinates (x
,y
,z
)andletS have coordinates (x, y, z).
If δ(x
,y
,z
) denotes the density of P, then the potential energy acting on S takes
the form
U(x, y, z)=G
|P|
δ(x
,y
,z
)
Δ
dx
dy
dz
,
where |P| represents the volume of P and Δ is the distance between Q and S:
Δ ≡
(x − x
)
2
+(y − y
)
2
+(z − z
)
2
.
The equations of motion are given by
¨x =
∂U
∂x
, ¨y =
∂U
∂y
, ¨z =
∂U
∂z
.
If r denotes the distance between S and O, ρ is the distance OQ and α is the angle
formed by OS and OQ,thenΔ
2
= r
2
+ ρ
2
− 2rρ cos α. Therefore, we can expand
1
Δ
using the Legendre polynomials P
n
and we can write the potential function as
U ≡
∞
n=0
U
n
=
G
r
|P|
δ(x
,y
,z
)
∞
n=0
ρ
r
n
P
n
(cos α) dx
dy
dz
. (5.25)
98 5 Rotational dynamics
Explicit computations for the first few terms provide
U
0
=
GM
r
U
1
=0
U
2
=
G
r
3
1
2
(I
1
+ I
2
+ I
3
) −
3
2r
2
(I
1
x
2
+ I
2
y
2
+ I
3
z
2
)
.
Introducing the polar coordinates (r, φ, θ), where (φ, θ) are the satellite’s longitude
and latitude, defined through the relations
x = r cos φ cos θ
y = r sin φ cos θ
z = r sin θ,
one finds
U
2
=
G
r
3
I
3
−
I
1
+ I
2
2
1
2
−
3
2
sin
2
θ
−
3
4
(I
1
− I
2
)cos
2
θ cos 2φ
. (5.26)
In the gyroscopic case I
1
= I
2
, the potential (5.26) reduces to
U
2
=
GMR
2
e
r
3
J
2
1
2
−
3
2
sin
2
θ
, (5.27)
where
J
2
≡
I
3
− I
1
MR
2
e
and R
e
is the equatorial’s radius of P.
For a body with spherical symmetry I
1
= I
2
= I
3
, one finds
U =
GM
r
.
In general, for a body symmetric with respect to the equatorial plane, the odd
terms of the development (5.25) are zero and one can write the potential energy as
U =
GM
r
1 −
∞
n=1
R
e
r
2n
J
2n
P
2n
(sin θ)
for suitable coefficients J
2n
, called the zonal coefficients [103].
5.7 Interaction between two bodies of finite dimensions
Let P and P
be two bodies of finite dimensions with masses M, M
and centers
of mass O, O
.Let(O,x,y,z) be a reference frame centered in O with the x–axis
along the direction OO
.Letr be the distance between O and O
.IfdM represents
an element of mass of P with coordinates (x
M
,y
M
,z
M
) with respect to (O,x,y,z)

5.8 The tether satellite 99
and dM
is an element of mass of P
with coordinates (x
M
,y
M
,z
M
) with respect
to (O
,x,y,z), then the potential energy can be written as
U = G
P
P
dMdM
Δ
,
where Δ denotes the distance between dM and dM
, namely
Δ=
(r + x
M
− x
M
)
2
+(y
M
− y
M
)
2
+(z
M
− z
M
)
2
.
Introducing the quantities
ρ =
1
r
(x
M
− x
M
)
2
+(y
M
− y
M
)
2
+(z
M
− z
M
)
2
,α=
x
M
− x
M
rρ
,
we obtain
Δ=r
1 − 2αρ + ρ
2
.
Finally, using Legendre polynomials one can expand the potential energy as
U = G
P
P
dMdM
r
∞
n=0
P
n
(α)ρ
n
. (5.28)
If (a, b, c)and(a
,b
,c
) denote the direction cosines of OO
relative to the principal
axes of, respectively, P and P
, then the first few terms of (5.28) can be written as
U
0
=
GMM
r
U
1
=0
U
2
=
GM
r
3
1
2
(I
1
+ I
2
+ I
3
) −
3
2
(I
1
a
2
+ I
2
b
2
+ I
3
c
2
)
+
GM
r
3
1
2
(I
1
+ I
2
+ I
3
) −
3
2
(I
1
a
2
+ I
2
b
2
+ I
3
c
2
)
,
where (I
1
,I
2
,I
3
) are the principal moments of inertia of P, while (I
1
,I
2
,I
3
) refer
to P
. Higher–order terms can be constructed in a similar way.
5.8 The tether satellite
The tether satellite is formed by two points P
1
and P
2
with masses m
1
and m
2
connected by an extensible, massless tether (see [161] and references by the same
author); the center of mass O of P
1
and P
2
is supposed to move under the grav-
itational attraction of a body P with mass M. The average distance R between
O and P is much larger then the maximal distance d between m
1
and m
2
.We
assume that O moves on a Keplerian orbit with eccentricity e and semimajor axis
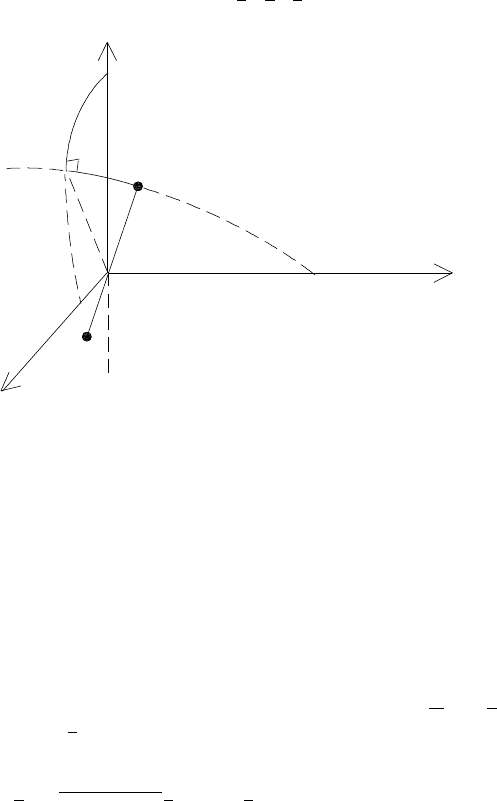
a; its position on the ellipse is characterized by the true anomaly f.Let(O,x,y,z)
be the orbital reference frame oriented as in Figure 5.5 and let e
x
,e
y
,e
z
be the

100 5 Rotational dynamics
O
z
#
'
m
2
m
1
y
x
Fig. 5.5. The orbital reference frame (O,x,y,z) of the tether satellite.
corresponding unit vectors. If d
0
is the maximal length of the tether, we denote by
ξ the relative extension defined as
ξ =
d
d
0
− 1 ,
where we assume that ξ>0. Moreover, let ϑ be the angle formed by the z–axis
with the projection of the tether on the orbital plane xz and let ϕ be the angle
formed by the direction of the tether with this plane.
The expressions for the kinetic and potential energy of the attitude dynamics
can be obtained as follows (see, e.g., [41]). Let us write the potential energy as
Π=Π
g
+Π
e
,
where Π
g
is the gravitational contribution, while Π
e
is due to the elastic energy
caused by the tether extension. Let R
= Re
z
be the radius vector OP and r
i
,
i =1, 2, be the radius vector joining the mass m
i
with O:
r
i
=
(−1)
i
m
3−i
d
0
m
1
+ m
2
(1 + ξ)e
d
,e
d
=
⎛
⎝
cos ϕ sin ϑ
−sin ϕ
cos ϕ cos ϑ
⎞
⎠
. (5.29)
We can write Π
g
as the sum of the contributions due to m
1
and m
2
:
Π
g
=Π
g
1
+Π
g
2
,
where
Π
g
i
= −
GMm
i
|R + r
i
|
i =1, 2 ,

5.8 The tether satellite 101
which can be expanded as
Π
g
i
= −
GMm
i
R
1 −
e
z
· r
i
R
−
1
2R
2
[r
2
i
− 3(e
z
· r
i
)
2
]+...
,i=1, 2 .
Let us write the gravitational energy Π
g
as the sum
Π
g
=Π
g
0
+Π
g
r
,
where Π
g
0
is independent of the tether orientation and extension, namely
Π
g
0
= −
GM(m
1
+ m
2
)
R
,
while Π
g
r
is given by
Π
g
r
=
GMm
0
d
2
0
2R
3
(1 + ξ)
2
1 − (e
z
· e
d
)
2
+ ... , (5.30)
where m
0
is the reduced mass:
m
0
=
m
1
m
2
m
1
+ m
2
.
Notice that the following Keplerian relation holds:
GM
R
3
= n
2
a
R
3
=
n
2
(1 + e cos f )
3
(1 − e
2
)
3
,
where n is the mean motion and f is the true anomaly of the Keplerian orbit of
O with respect to P. According to Hooke’s law, the contribution due to the elastic
deformation is given by
Π
e
=
cd
2
0
ξ
2
2
,
where c denotes the stiffness of the tether.
The kinetic energy T is given by the sum of the contributions due to m
1
and
m
2
, namely
T = T
1
+ T
2
, where T
i
=
m
i
V
2
i
2
,i=1, 2 .
We denote by V
i
= |V
i
| the modulus of the velocity vector
V
i
= V
0
+ v
i
,
where V
0
represents the velocity of the barycenter and v
i
is the velocity of the mass
m
i
with respect to O.LetΩ=Ω(f) denote the angular velocity of the Keplerian
motion:
Ω
=Ω(f)e
y
, where Ω(f)=
n(1 + e cos f )
2
(1 − e
2
)
3/2
.

102 5 Rotational dynamics
Then v
i
can be written as
v
i
=
d
∗
r
i
dt
+Ω
∧ r
i
,
where the operator d
∗
/dt denotes differentiation in the non–inertial orbital reference
frame (O,x,y,z). Using (5.29) we obtain
d
∗
r
i
dt
=
(−1)
i
m
3−i
d
0
m
1
+ m
2
˙
ξe
d
+(1+ξ)
d
∗
e
d
dt
,
where
d
∗
e
d
dt
=
⎛
⎝
− ˙ϕ sin ϕ sin ϑ +
˙
ϑ cos ϕ cos ϑ
− ˙ϕ cos ϕ
− ˙ϕ sin ϕ cos ϑ −
˙
ϑ cos ϕ sin ϑ
⎞
⎠
.
Finally, the kinetic energy can be expressed as the sum (see [41])
T = T
0
+ T
r
,
where
T
0
=
(m
1
+ m
2
)V
2
0
2
and
T
r
=
m
0
d
2
0
2
˙
ξ
2
+(1+ξ)
2
˙ϕ
2
+(
˙
ϑ +Ω(f))
2
cos
2
ϕ
.
The Lagrangian function describing the tether’s attitude dynamics
3
is given by
L = T
r
− (Π
g
r
+Π
e
) , (5.31)
where the terms T
0
and Π
g
0
have been omitted, since they do not depend on the
attitude variables. It is convenient to adopt the true anomaly f as the independent
variable. Let us denote by p
ϑ
, p
ϕ
, p
ξ
the canonical momenta conjugated to ϑ,
ϕ, ξ. Retaining only the lowest–order terms in (5.30), the Hamiltonian function
associated to (5.31) takes the form
H(p
ϑ
,p
ϕ
,p
ξ
,ϑ,ϕ,ξ,f)=
1
2(1 + e cos f)
2
(1 + ξ)
2
(p
ϑ
+1)
2
cos
2
ϕ
+ p
2
ϕ
+(1+ξ)
2
p
2
ξ
− p
ϑ
+
1
2
(1 + ξ)
2
(1 + e cos f )(1 − 3cos
2
ϑ cos
2
ϕ)
+
(1 − e
2
)
3
2β(1 + e cos f)
2
ξ
2
, (5.32)
where the dimensionless parameter β in (5.32) denotes the relative stiffness of the
tether, namely
β =
m
0
n
2
c
.
3
By attitude dynamics we intend the study of the orientation of the satellite in a given
reference frame.
5.9 The dumbbell satellite 103
5.9 The dumbbell satellite
A particular case of tether dynamics is obtained whenever β goes to zero, thus
yielding a dumbbell satellite composed by two points P
1
and P
2
with masses m
1
and m
2
connected by a non–extensible, massless rod of length d (see, e.g., [41] for
full details). The center of mass O of P
1
and P
2
is assumed to move under the
influence of the gravitational attraction of a body P with mass M.LetR be the
average distance between O and P, which is taken to be much larger than d.We
assume that O moves on a Keplerian orbit with eccentricity e and semimajor axis
a.Let(O,x,y,z) be a reference frame with the z–axis oriented along the local
vertical, the y–axis perpendicular to the orbital plane and the x–axis forming an
oriented frame (see Figure 5.6). Denote by e
x
,e
y
,e
z
the corresponding unit vectors.
O
#
'
m
2
m
1
x
y
z
Fig. 5.6. The definition of the orbital reference frame (O,x,y,z).
In order to study the attitude dynamics of the dumbbell satellite, we introduce
the angle ϕ formed by the direction of the rod with the xz–plane and the angle ϑ
formed by the z–axis with the projection of the rod on the orbital plane (Figure 5.7).
As usual, let f be the true anomaly of the Keplerian orbit.
The Lagrangian function describing the motion of the dumbbell satellite is the
difference between the kinetic energy and the potential energy, which are defined
as follows [41]. Let us write the potential energy as the sum
Π=Π
1
+Π
2
, (5.33)
where Π
1
and Π
2
are the contributions due to m
1
and m
2
.SetR
= Re
z
equal to
the radius vector OP, r
i
as the radius vector of the mass m
i
with respect to O:
r
i
=
(−1)
i
m
3−i
d
m
1
+ m
2
e
d
,e
d
=
⎛
⎝
cos ϕ sin ϑ
−sin ϕ
cos ϕ cos ϑ
⎞
⎠
;
