Celletti A. Stability and Chaos in Celestial Mechanics

Подождите немного. Документ загружается.

84 5 Rotational dynamics

Fig. 5.1. Euler angles.

In the body reference frame the components (ω

,ω

) of the angular velocity

of rotation are derived as follows. Since

ϑ has the same direction as n

, while ˙ϕ is

aligned with K

and

ψ with k, their projections on the body reference frame are

given by:

ϑ cos ψ ˙ϕ

=˙ϕ sin ϑ sin ψ

= −

ϑ sin ψ ˙ϕ

=˙ϕ sin ϑ cos ψ

=0 ˙ϕ

=˙ϕ cos ϑ

ψ.

Therefore we get:

=˙ϕ sin ϑ sin ψ +

ϑ cos ψ

=˙ϕ sin ϑ cos ψ −

ϑ sin ψ

=˙ϕ cos ϑ +

ψ. (5.1)

Let I

, I

be the principal moments of inertia of the rigid body S, which is as-

sumed to be subject to a force with potential energy V (ϕ, ψ, ϑ) [5]. The Lagrangian

function describing the motion is given by

ϑ, ˙ϕ,

ψ, ϑ,ϕ, ψ)=

+ I

) − V (ϕ, ψ, ϑ)

(˙ϕ sin ϑ sin ψ +

ϑ cos ψ)

(˙ϕ sin ϑ cos ψ −

ϑ sin ψ)

(˙ϕ cos ϑ +

ψ)

− V (ϕ, ψ, ϑ) .

It is readily seen that the energy is preserved. The rigid body is said to have a

gyroscopic structure whenever two moments of inertia coincide, say I

= I

with

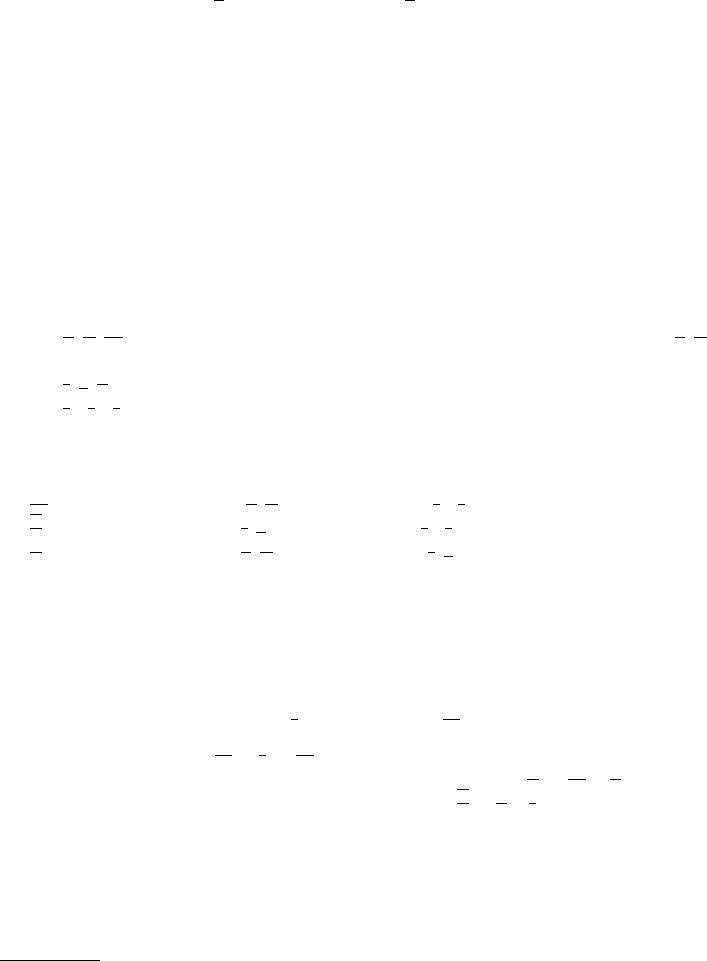
5.2 Andoyer–Deprit variables 85

= I

; in this case the Lagrangian function takes the form

ϑ, ˙ϕ,

ψ, ϕ,ψ, ϑ)=

(

+˙ϕ

sin

ϑ)+

(˙ϕ cos ϑ +

ψ)

− V (ϕ, ψ, ϑ) .

For the free rigid body motion the momenta conjugated to ϕ and ψ are constants,

since the kinetic part depends only on the angle ϑ.

5.2 Andoyer–Deprit variables

The rigid body dynamics can be conveniently described through a set of action–

angle coordinates, known as Andoyer–Deprit variables [55]. In the general case in

which the rotation axis does not necessarily coincide with a principal direction, we

introduce three reference frames with the same origin O located at the center of

mass:

– (O,I

,J,K)isaninertial reference frame, for example with the plane (I,J)

coinciding with the ecliptic plane (or the Laplace plane

) at some epoch;

– (O,i

,j,k)isabody frame, with the axes coinciding with the principal axes;

– (O,i

)isaspin frame, with the vertical axis aligned with the angular

momentum.

We introduce the following lines of nodes:

– m

is the intersection of (I,J) with the plane (i

);

–

n is the intersection of (i,j) with the plane (i

);

– n

is the intersection of (I,J) with the plane (i,j).

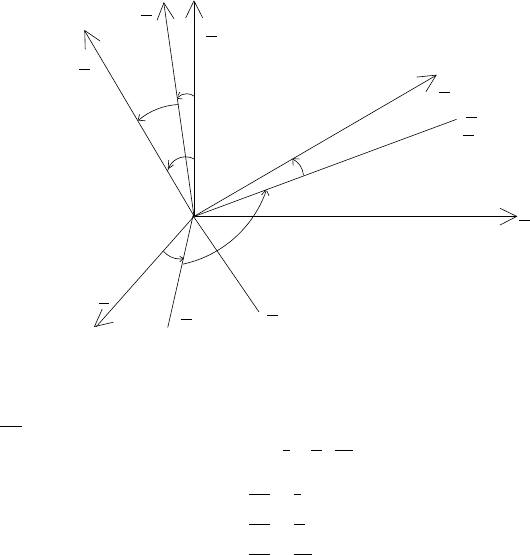
The angles ϕ, ψ, ϑ, g, , h, J, K are deﬁned as follows (see also Figure 5.2):

– (ϑ, ϕ, ψ) are the Euler angles of the body frame with respect to the inertial

frame;

– (J, g, ) are the Euler angles of the body frame with respect to the spin frame;

– (K, h, 0) are the Euler angles of the inertial frame with respect to the spin

frame, where we assume that i

coincides with m.

We also remark that m

≡ i

∧K denotes the line of nodes between the inertial

plane and the plane orthogonal to the angular momentum; n

≡ K ∧ k is the line

of nodes between the inertial and equatorial planes;

n ≡ k ∧i

is the line of nodes

between the equatorial plane and the plane orthogonal to the angular momentum;

the angle g provides the motion of the equatorial axis with respect to the inertial

frame; the angle  gives the motion of the angular momentum with respect to the

body frame; the angle h provides the motion of the angular momentum with respect

to the inertial frame; the angle ϑ is formed by the direction of the vertical principal

axis of the ellipsoid with the vertical axis of the inertial frame.

The Laplace plane can be deﬁned as the plane with respect to which the orbital incli-

nation has a constant value.

86 5 Rotational dynamics

Fig. 5.2. Andoyer–Deprit angles.

If M

denotes the angular momentum, we introduce the following variables

deﬁned as the projections on the axes i

, k, K:

G ≡ M

· i

= M

L ≡ M

· k = G cos J

H ≡ M

· K = G cos K, (5.2)

where J is the so–called non–principal rotation angle formed by the vertical axes

of the spin and body frames, while K is the so–called obliquity angle formed by the

vertical axes of the spin and inertial frames. We denote by

(G, g), (L, ), (H, h)

the Andoyer–Deprit variables. Let p

, p

be the momenta conjugated to the

Euler angles. Their relations with the Andoyer–Deprit variables are the following:

= H

= L

= G sin J sin( − ψ) . (5.3)

Proposition. The transformation from (p

,ϕ,ψ,ϑ) to (G, L, H, g, , h) is

canonical.

Proof. To prove the canonicity of the transformation we need to show that (see,

e.g. [5])

Gdg + Ld + Hdh = p

dϕ + p

dψ + p

dϑ . (5.4)

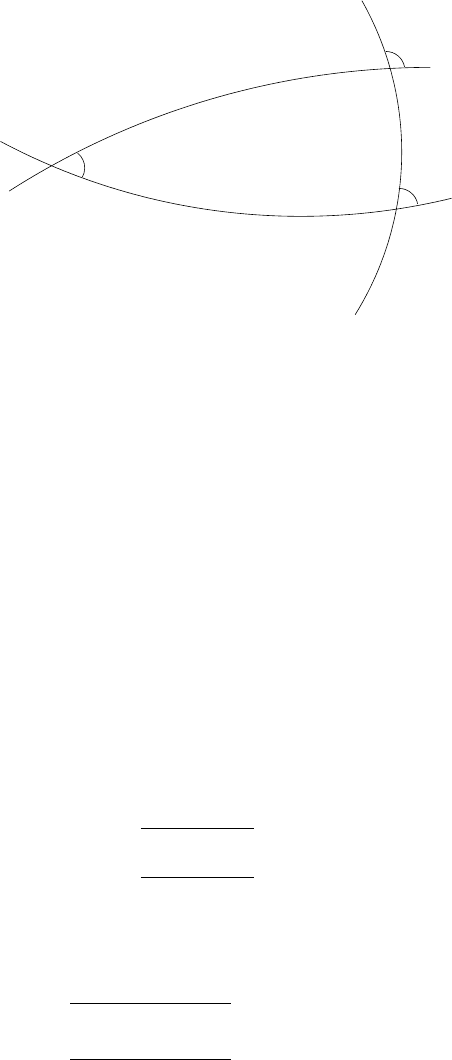
5.3 Free rigid body motion 87

Ã –`

' –`

Fig. 5.3. A spherical triangle.

From properties of spherical trigonometry applied to the spherical triangle of Fig-

ure 5.3, one obtains:

dg = −sin J sin(ψ − )dϑ +cosKd(ϕ − h)+cosJd(ψ − ) .

Using (5.3) it is readily proved that (5.4) holds. 

5.3 Free rigid body motion

Taking into account the relations (5.1) we can express the momenta conjugated to

the Euler angles as

=(I

sin ψ + I

cos ψ)sinϑ + I

cos ϑ

= I

cos ψ − I

sin ψ

= I

. (5.5)

Inverting (5.5) one obtains

− p

cos ϑ

sin ϑ

sin ψ + p

cos ψ

− p

cos ϑ

sin ϑ

cos ψ − p

sin ψ

= p

. (5.6)

Using the relations (5.2), (5.3) and (5.6) one ﬁnds:

= G



cos K −cos J cos ϑ

sin ϑ

sin ψ +sinJ sin( − ψ)cosψ



= G



cos K −cos J cos ϑ

sin ϑ

cos ψ − sin J sin( − ψ)sinψ



= L. (5.7)

88 5 Rotational dynamics

From elementary properties of spherical trigonometry applied to the triangle of

Figure 5.3, one ﬁnds

cos K =cosJ cos ϑ +sinJ sin ϑ cos(ψ − );

together with (5.7) this relation provides

= G sin J sin 

= G sin J cos 

= L.

Finally, we can write the Hamiltonian of a free rigid body motion as

H(G, L, H, g, , h)=

− L

)



sin



cos





which does not depend on H as well as on the angles g and h. Notice that in the

gyroscopic case I

= I

the Hamiltonian function becomes:

H(G, L, H, g, , h)=

− L

, (5.8)

which does not depend on H as well as on the angles g,  and h. Therefore, the

associated Hamilton’s equations provide that the actions (G, L, H) are constants.

As for the angles, one has

˙g =

 =



−



h =0,

which means that the rigid body rotates around the symmetry axis with constant

velocity and that it precedes with uniform velocity.

Remark. The Andoyer–Deprit variables are not well–deﬁned if K =0orJ =0;

in these situations one can introduce a transformation to non–singular variables

deﬁned as

=  + g + hΛ

= G

= −Λ

= G − L = G(1 − cos J)

= −hΛ

= G − H = G(1 − cos K) . (5.9)

The corresponding Hamiltonian is given by

H(Λ

,Λ

,λ

(Λ

− Λ

)



−(Λ

−Λ

)



sin

cos



Consider a spherical triangle with angles A, B, C and opposite sides a, b, c; then:

cos A = −cos B cos C +sinB sin C cos a.

5.4 Perturbed rigid body motion 89

5.4 Perturbed rigid body motion

Let the rigid body S of mass m be subject to the gravitational attraction of a

perturber point–mass body P with mass M. We assume that the rigid body moves

on a Keplerian orbit with instantaneous orbital radius vector r

, joining P with the

barycenter of S; denoting by |S| thevolumeofS and by x

the position vector with

respect to the barycenter of a generic point of the rigid body, the potential takes

the form

V ≡−



GMm

|r + x|

|S|

. (5.10)

The development of

V in spherical harmonics is given by (see [57, 103, 112])

V = −GM

∞



i=0



j=0

i+1

(sin θ)(C

cos jφ + S

sin jφ) ,

where (r, φ, θ) are, respectively, the modulus of r

, the longitude φ and the latitude

θ measured eastward in a reference frame with origin in the barycenter of the

rigid body, C

and S

are the potential coeﬃcients whichdependonthedensity

distribution of the rigid body, P

are the Legendre associated functions deﬁned by

the set of equations

(sin θ) ≡ cos



k=0

ijk

sin

i−j−2k

θ, n=



i − j



ijk

≡

(−1)

(2i − 2k)!

k!(i − k)!(i − j − 2k)!

The lowest signiﬁcative order of the development of the potential, say

,isgiven

= −

GMm







(sin θ)+C

(sin θ) cos 2φ



, (5.11)

where R

is the body’s equatorial radius and P

(sin θ) is the Legendre polynomial

of second order; the spherical harmonic terms C

, C

are given by

≡

+ I

− 2I

) ,C

≡

− I

) .

Let us denote by (˜x, ˜y, ˜z) the coordinates of the unitary vector oriented toward P

in the body frame, namely

˜x =cosφ cos θ

˜y =sinφ cos θ

˜z =sinθ.

90 5 Rotational dynamics

Then, we can write an expression for P

(sin θ), P

(sin θ) cos 2φ in terms of (˜x, ˜y, ˜z)

(sin θ)=

2˜z

− ˜x

− ˜y

(sin θ) cos 2φ =3(˜x

− ˜y

) .

In order to express (˜x, ˜y, ˜z) with respect to the inertial frame we need to deﬁne

the matrices R

(α), R

(α) as the rotations of angle α with the subscript

denoting the rotation axis. Denoting by f thetrueanomalyofS along its Keplerian

orbit, we obtain:

⎛

⎝

˜x

˜y

˜z

⎞

⎠

= R

()R

(J)R

(g)R

(K)R

(h)

⎛

⎝

cos f

sin f

⎞

⎠

. (5.12)

In the general case, encompassing also J and K close to zero, one introduces non–

singular angles as in (5.9) by deﬁning λ

=  + g + h, in terms of which we provide

the following deﬁnition of spin–orbit resonance.

Deﬁnition. A spin–orbit resonance of order p : q,forp, q ∈ Z with q = 0, occurs

whenever the ratio of the rates of variation of λ

and of the mean anomaly 

equal to p/q, namely



. (5.13)

The relation (5.13) means that during q revolutions around P, the body S makes

p rotations about its spin–axis. The associated resonant angle is equal to

σ ≡

qλ

− p

The synchronous resonance is characterized by p = q = 1, which implies that the

body always points the same face toward the perturber, since the period of rotation

around the spin–axis coincides with the period of revolution about P. This is the

case of the Moon–Earth system, where astronomical data provide that the period

of revolution of the Moon around the Earth and the period of rotation about the

spin–axis are equal to 27.322 days.

At the end of the 17th century G.D. Cassini formulated three laws about the motion

of the Moon around the Earth. Observing that an equilibrium state is provided by

J = K = 0 and by σ =  = h = 0, the Cassini laws can be expressed as follows:

(1) the Moon rotates around a principal axis in a synchronous resonance;

(2) the spin–axis and the orbit normal form a constant angle (which means that

K is constant);

(3) the spin–axis, the orbit normal and the ecliptic normal lie in the same plane.

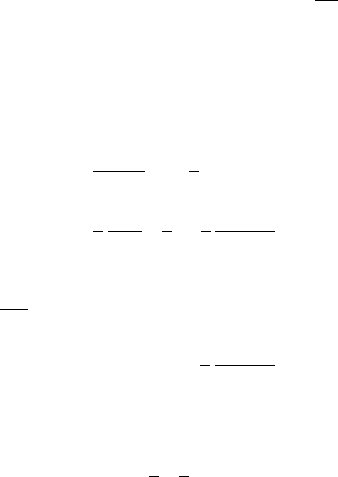
5.5 The spin–orbit problem 91

5.5 The spin–orbit problem

A simple paradigmatic model of rotational dynamics is provided by the spin–orbit

problem (see, e.g., [23,172]) obtained by setting to zero the non–principal rotation

angle as well as the obliquity: J = K =0.InthiscaseG = L = H, namely

= Λ

= 0, while the kinetic part reduces to

. Also the potential energy

simpliﬁes, since for J = K = 0, taking into account (5.12), we obtain

˜x = cos(f − λ

) , ˜y =sin(f − λ

) , ˜z =0.

The above relations imply that the non–trivial term in

is provided by

= −

GMm







(˜x

− ˜y

)



= −





− I

cos(2λ

− 2f) .

We adopt the units of measure such that the mean motion, which by Kepler’s law

coincides with

, is equal to one. We deﬁne the equatorial ellipticity as

ε ≡

− I

;

as a consequence, the potential can be written as:

= −





cos(2λ

− 2f) .

We will specify two diﬀerent spin–orbit models: the ﬁrst one is subject only to

the gravitational attraction of the perturber, while the second model takes into

account a dissipative contribution due to the internal non–rigidity of the body.

The two models will be referred to as the conservative and dissipative spin–orbit

problems.

5.5.1 The conservative spin–orbit problem

Consider the motion of a rigid body S with triaxial structure, under the gravita-

tional inﬂuence of a point–mass perturber P. We assume that

(i) S moves on an elliptic Keplerian orbit with semimajor axis a and eccentricity

e (namely, the perturbations due to other bodies are neglected);

(ii) the spin–axis coincides with the smallest physical axis of the ellipsoid (namely,

with the largest principal axis of inertia so that J =0);

(iii) the spin–axis is perpendicular to the orbital plane (namely, the obliquity K is

zero);

(iv) dissipative eﬀects are neglected.

92 5 Rotational dynamics

Under such assumptions the Hamiltonian governing the dynamics is given by

(Λ

,λ

,t)=

−





cos(2λ

− 2f) , (5.14)

where it is intended that the Hamiltonian depends upon the time through the

quantities r and f . Making the change of variables y =

, x = λ

, then (5.14)

reduces to

H(y, x, t)=

−





cos(2x − 2f) .

The corresponding Hamilton’s equations are

˙y = −ε





sin(2x − 2f)

˙x = y, (5.15)

which are equivalent to

¨x + ε





sin(2x − 2f)=0. (5.16)

In the spin–orbit problem the quantity x denotes the angle formed by the direction

of the largest physical axis (which by assumptions (ii)and(iii) belongs to the

orbital plane) with a reference axis, say the perihelion line (see Figure 5.4).

Fig. 5.4. The geometry of the spin–orbit problem.

Remarks.

(a) The Moon, as well as most of the evolved satellites of the solar system, are

observed to move in a synchronous resonance; the only exception is provided by

Mercury [48], which moves in a 3:2 spin–orbit resonance, since the orbital period is

equal to the rotational period within an error of the order of 10

−4

. It means that,

almost exactly, during two orbital revolutions around the Sun, Mercury makes three

rotations about its spin–axis.

(b) The parameter ε =

−I

is zero in the case of equatorial symmetry I

= I

.In

this case the equation of motion is trivially integrable. For regular bodies like the

5.5 The spin–orbit problem 93

Moon or Mercury, the parameter ε is of the order of 10

−4

and the corresponding

dynamical system is nearly–integrable.

determined through the Keplerian relations:

r = a(1 − ecosu)

f = 2 arctan



1+e

1 − e

tan

, (5.17)

where u is related to the mean anomaly 

by means of Kepler’s equation



= u − esinu.

(d) The orbital radius and the true anomaly depend on the eccentricity e; for e = 0

one has r = a, f = t + t

for a suitable constant t

; henceforth, for circular orbits

(5.16) reduces to the integrable equation ¨x + ε sin(2x − 2t − 2t

)=0.

(e) Considering the lift of the angle x on R, we interpret a p : q spin–orbit resonance

for p, q ∈ Z with q>0 as a periodic solution for (5.16), say t ∈ R → x = x(t) ∈ R,

such that

x(t +2πq)=x(t)+2πp for any t ∈ R .

Expanding (5.17) in power series of the orbital eccentricity, equation (5.16) can

be developed in Fourier series as

¨x + ε

+∞



m=0,m=−∞



, e



sin(2x − mt)=0, (5.18)

where the expressions of the ﬁrst few coeﬃcients W (

, e) are reported in Table 5.1;

the coeﬃcients have been expanded in power series of the orbital eccentricity as

W (

, e) ≡ W

(e) + W

(e) + ...,beingW

(e) = O(e

Table 5.1. Expansion in powers of the orbital eccentricity of the coeﬃcients W (

, e)

appearing in (5.18).

(e) W

(e)

−1

240

−

11e

768

313e

30720

−

384

−

143e

18432

1 1 −

13e

−

35e

288

−

123e

489e

128

−

1763e

2048

17e

−

115e

601e

845e

−

32525e

768

208225e

6144

533e

−

13827e

160