Celletti A. Stability and Chaos in Celestial Mechanics
Подождите немного. Документ загружается.


234 A Basics of Hamiltonian dynamics
then, one has:
˙
I
=
∂h(I
)
∂ϕ
=0
˙ϕ =
∂h(I
)
∂I
= ω(I) .
Therefore the action I
is constant along the motion, namely I = I
0
, while the
second equation provides the variation of the angle ϕ
as a function of the time:
ϕ
= ω(I
0
)t + ϕ
0
,where(I
0
,ϕ
0
) denote the initial conditions.
In action–angle variables a system is nearly–integrable if it can be written as
H(I
,ϕ)=h(I)+εf(I,ϕ) ,
where h(I
) represents the integrable part, εf(I,ϕ) is the perturbing function and ε
is the perturbing parameter measuring a small variation from the integrable case.
In the three–body problem, the integrable part coincides with the Keplerian two–
body interaction, while the perturbing function provides the gravitational attrac-
tion with the third body and the perturbing parameter is the mass ratio of the
primaries.
Example. Let us determine the action–angle variables for the harmonic oscillator
described by the Hamiltonian
H(p, q)=
1
2m
(p
2
+ ω
2
q
2
) .
Setting H(p, q)=E, one has
p
2
=2mE − ω
2
q
2
and the corresponding action variable is:
I =
)
pdq =
)
2mE − ω
2
q
2
dq .
Let q =
2mE
ω
2
sin ϑ; then, one has:
I =
2π
0
2mE − 2mE sin
2
ϑ
2mE
ω
2
cos ϑdϑ
=
2mE
ω
2π
0
cos
2
ϑdϑ =
2πmE
ω
.
The Hamiltonian in action–angle variables becomes:
E = H(I)=
ω
2πm
I.

A.4 Action–angle variables 235
The associated Hamilton’s equations are
˙
I =0
˙ϕ =
ω
2πm
,
whose solution is found to be
I(t)=I(0)
ϕ(t)=
ω
2πm
t + ϕ(0) .
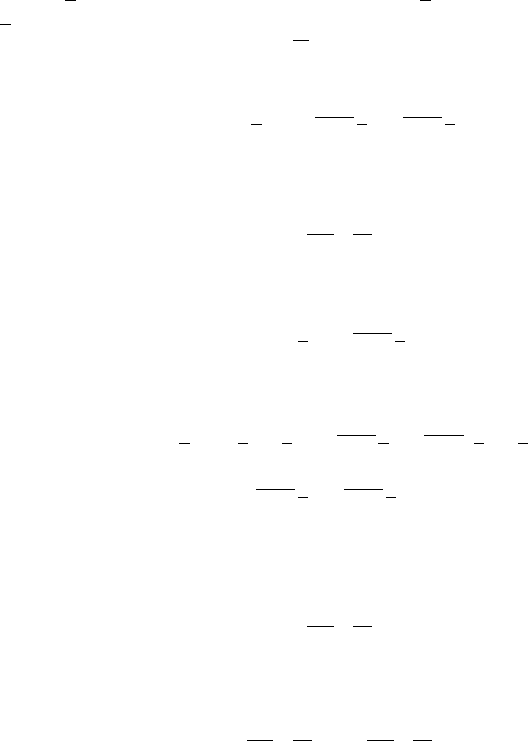
B The sphere of influence
Assume that a small body P
2
of negligible mass moves under the influence of two
point–mass bodies P
1
and P
3
with masses, respectively, m
1
and m
3
. An estimate
of the region where the motion is dominated by the influence of P
1
or that of P
3
,
namely the respective sphere of influence, is obtained as follows.
Let d
1
be the distance vector from P
2
to P
1
, d
3
that joining P
2
and P
3
,andlet
d
be the distance vector between P
1
and P
3
.Letd
1
, d
3
, d be their norms; if P
2
is
close to P
3
, we can assume that
d
3
d
is small, so that d
1
d. The motion of P
2
is
governed by the equations:
¨
d
1
= −
Gm
1
d
3
1
d
1
−
Gm
3
d
3
3
d
3
and the ratio of the gravitational attraction exerted by P
3
to that exerted by P
1
is given by the term
m
3
m
1
d
d
3
2
.
The motion of P
3
is ruled by the equation
¨
d
= −
Gm
1
d
3
d .
Therefore, one obtains:
¨
d
3
=
¨
d
1
−
¨
d = −
Gm
3
d
3
3
d
3
−
Gm
1
d
3
(d
1
− d)
= −
Gm
3
d
3
3
d
3
−
Gm
1
d
3
d
3
.
As a consequence, the ratio of the gravitational attraction exerted by P
1
to that
exerted by P
3
is given by the term
m
1
m
3
d
3
d
3
.
Finally, we can conclude that the influence of P
3
is dominant whenever
m
1
m
3
d
3
d
3
<
m
3
m
1
d
d
3
2
,

238 B The sphere of influence
which leads to define the sphere of influence around P
3
of radius r given by
r ≡
m
3
m
1
2
5
d.
As a concrete example, we identify P
1
with the Sun and P
3
with the Earth. Then,
m
1
=2·10
30
kg, m
3
=5.97 ·10
24
kg, d =1.5 ·10
8
km, so that the Earth’s sphere of
influence has a radius approximately equal to r =9.25 ·10
5
km, which amounts to
about 2.4 times the Earth–Moon distance. As for Jupiter, taking m
3
=1.9·10
27
kg
and d =7.8 · 10
8
km, one finds that r =4.82 · 10
7
km, amounting to more than
125 times the Earth–Moon distance.
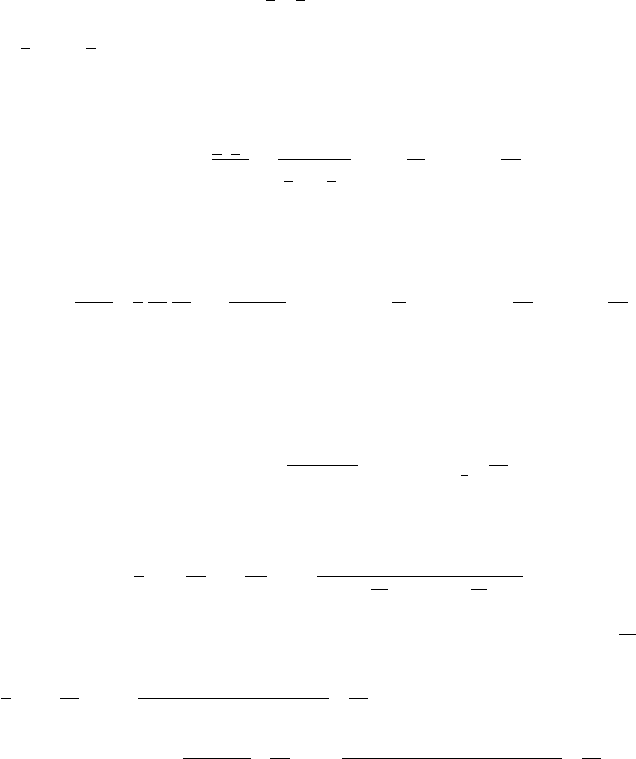
C Expansion of the perturbing function
Let P
1
, P
2
, P
3
be three point–mass bodies with masses, respectively, m
1
, m
2
, m
3
.
In the framework of the three–body problem, we investigate the motion of P
2
under
the influence of P
1
and P
3
.Letr
2
, r
3
be the radius vectors associated to P
1
P
2
and
to P
1
P
3
,andletr
2
, r
3
be their sizes with r
2
<r
3
.Letψ be the angle formed
by r
2
and r
3
. Denote by f
2
, f
3
the true anomalies of the osculating orbits of P
2
,
P
3
around P
1
and let g
2
, g
3
be their arguments of perihelion. Let ϑ
2
= f
2
+ g
2
,
ϑ
3
= f
3
+ g
3
and define γ =cosψ − cos(ϑ
2
− ϑ
3
). If ε is the m
1
/m
3
mass ratio,
then the perturbing function associated to P
2
can be written as
R = −ε
r
1
r
3
r
3
3
+
ε
|r
1
− r
3
|
= −ε
r
1
r
2
3
cos ψ +
ε
a
3
R
,
wherewedenotebya
2
, a
3
the semimajor axes of P
2
, P
3
and we expand R
as (see
[61])
R
=
∞
i=0
(2i)!
(i!)
2
1
2
r
2
a
2
r
3
a
3
γ
i
a
i
2
a
i+1
3
2
∞
j=−∞
"
∞
=0
1
!
k=0
k
r
2
a
2
− 1
k
r
3
a
3
− 1
−k
Γ
i,j,k,−k
cos((ϑ
2
− ϑ
3
)j)
#
,
with
Γ
i,j,m,n
≡ a
m
2
a
n
3
∂
m+n
∂a
m
2
∂a
n
3
a
−2i−1
3
b
(j)
i+
1
2
a
2
a
3
,
where the Laplace coefficients b
(j)
s
are defined as
1
2
b
(j)
s
(
a
2
a
3
)=
1
2π
2π
0
cos(jϕ)
(1 − 2
a
2
a
3
cos ϕ +(
a
2
a
3
)
2
)
s
dϕ .
Notice that the Laplace coefficients can be expanded in power series of
a
2
a
3
as
1
2
b
(j)
s
a
2
a
3
=
s(s +1)...(s + j − 1)
1 · 2 · 3 ·····j
a
2
a
3
j
·
1+
s(s + j)
j +1
a
2
a
3
2
+
s(s +1)(s + j)(s + j +1)
2(j +1)(j +2)
a
2
a
3
4
+ ...
.

D Floquet theory and Lyapunov exponents
Floquet theory provides a tool for investigating the regular or chaotic behavior of a
dynamical system and it allows us to introduce the Lyapunov exponents. Referring
to the specialized literature for an exhaustive treatment of the topic, we briefly
introduce as follows the elementary notions related to Floquet theory.
Consider the dynamical system described by the differential equations
˙x
= A(t)x ,x∈ R
n
, (D.1)
where A = A(t)isann × n periodic matrix with period T . Floquet theory [93]
provides a transformation of coordinates, such that the analysis of (D.1) is reduced
to the study of a differential system with constant real coefficients.
Let Φ(t)betheprincipal monodromy or fundamental matrix, whose columns
are linear independent solutions of (D.1) and such that Φ(0) is the identity matrix.
After a period T one has
Φ(t + T )=Φ(t)Φ
−1
(0)Φ(T ) .
By the Floquet theorem [93], there exists a constant matrix B and a periodic
symplectic matrix C(t)suchthatatanytimet one has
Φ(t)=e
Bt
C(t) .
After the transformation y
= C
−1
(t)x, the system (D.1) is reduced to the following
differential equation with real constant coefficients:
˙y
= By .
The eigenvalues of Φ(T) are called the characteristic multipliers; they measure
the rate of expansion or contraction of a solution. A characteristic exponent is
aquantity such that e
T
is a characteristic multiplier. The real parts of the
characteristic exponents are the so–called Lyapunov exponents. When all Lyapunov
exponents are negative, the solution is asymptotically stable; when the Lyapunov
exponents are positive, the solution is unstable.
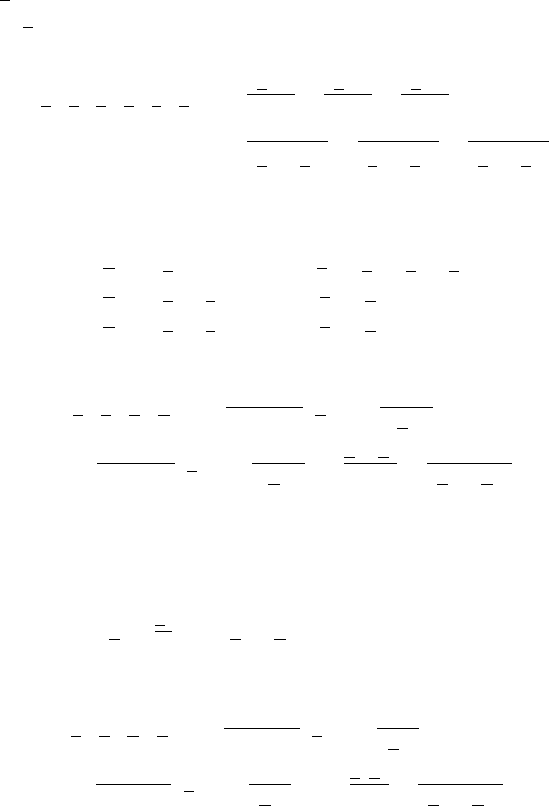
E The planetary problem
Consider three bodies P
1
, P
2
, P
3
of masses m
1
, m
2
, m
3
subject to the mutual
gravitational attraction. Assume that the three bodies move on the same plane
and let q
i
∈ R
2
, i =1, 2, 3, be their coordinates in an inertial reference frame;
denote by p
i
∈ R
2
, i =1, 2, 3, the conjugated momenta. Then, the Hamiltonian
function is given by
H
1
(p
1
,p
2
,p
3
,q
1
,q
2
,q
3
)=
p
1
2
2m
1
+
p
2
2
2m
2
+
p
3
2
2m
3
−
m
1
m
2
q
2
− q
1
−
m
1
m
3
q
3
− q
1
−
m
2
m
3
q
3
− q
2
.
We introduce heliocentric coordinates centered in P
1
by means of the change of
variables:
u
1
= q
1
,v
1
= p
1
+ p
2
+ p
3
u
2
= q
2
− q
1
,v
2
= p
2
u
3
= q
3
− q
1
,v
3
= p
3
.
The new Hamiltonian becomes:
H
2
(v
2
,v
3
,u
2
,u
3
)=
m
1
+ m
2
2m
1
m
2
v
2
2
−
m
1
m
2
u
2
+
m
1
+ m
3
2m
1
m
3
v
3
2
−
m
1
m
3
u
3
+
v
2
· v
3
m
1
−
m
2
m
3
u
2
− u
3
.
As in a planetary model, we assume that one mass (say, the star) is much larger
than the two others (say, the planets); as a consequence we rescale the masses as
m
1
= μ
1
, m
2
= εμ
2
, m
3
= εμ
3
,whereε is a small quantity and μ
i
, i =1, 2, 3, are
of order one. Applying the change of variables
˜v
i
=
v
i
ε
, ˜u
i
= u
i
,i=2, 3 ,
the new Hamiltonian is given by
H
3
(˜v
2
, ˜v
3
, ˜u
2
, ˜u
3
)=
μ
1
+ εμ
2
2μ
1
μ
2
˜v
2
2
−
μ
1
μ
2
˜u
2
+
μ
1
+ εμ
3
2μ
1
μ
3
˜v
3
2
−
μ
1
μ
3
˜u
3
+ ε
˜v
2
˜v
3
μ
1
−
μ
2
μ
3
˜u
2
− ˜u
3
,
