Casing/Tubing design manual october 2005 Chevron
Подождите немного. Документ загружается.


9.2 Stretch in a Vertical Wellbore, Single
String
Consider a tubular string run in a vertical wellbore. From its horizontal position on
the rack to a vertical position hanging in the wellbore, the tubular undergoes
several environmental changes that lead to change in length. These length
changes include:
9.2.1 Temperature
The length change due to temperature is:
(
)
δαδ
LLT
te ave
=
(9-1)
If the surface temperature is
and the gradient with true vertical depth, , is T
s
z
γ
T
, the average temperature change of a tubular string run between depths,
and
is,
z
1
z
2
(
)
[]
(
)
δγ
TT zz T zz
ave s T s T
=+ + −= +05 05
12 12
..
γ
(9-2)
and the temperature length change is,
(
)
δαγ
Lz
te T
=−05
2
2
1
2
. z
(9-3)
Note that the stretch because of temperature is not a function of the ambient
surface temperature.
9.2.2 Ballooning
The length change due to ballooning is:
(
)
(
)
δ
µ
δδ
L
E
pr pr
rr
L
pr
i
ave
io
ave
o
oi
=−
−
−
2
22
22
(9-4)
Assuming the surface pressures to be zero, and assuming the same fluid density
inside and out, the average pressure change of a tubular string run between
depths
and is, z
1
z
2
(
)
fave
zzp
γ
δ
21
5.0
+
=
(9-5)
and the ballooning length change is,
(
δ
µ
γ
L
E
zz
pr f
=−
2
2
1
2
)
(9-6)
Casing/Tubing Design Manual 9-3
October 2005

9.2.3 Weight (Gravity)
Because of its own (air) weight, the tube will stretch axially. This stretch
component can be calculated by noting that any differential element will be
subjected to a stress due to the weight of tube hanging below,
(
σγγγ
zs
z
z
s
z
z
s
A
Adz dz z z===
∫∫
1
22
2
)
−
(9-7)
so that the strain due to suspended tube below is,
(
ε
)
γ
z
s
E
zz=−
2
(9-8)
and the total stretch of the tube due to its own weight is,
() (
δ
γγ
L
E
zzdz
E
zz
wt
s
z
z
s
=−=−
∫
22
2
1
2
2
)
1
A
(9-9)
9.2.4 End Load
A hydrostatic force of magnitude
Fz
zf
=
−
γ
2
at the lower end of the tube
results in an axial stretch (equation 6-1, Chapter 6 – Tube Loads),
δ
δ
L
FL
EA
sh
z
= (9-10)
or
(
)
δ
γ
L
zz z
E
sh
f
=−
−
22 1
(9-11)
9.2.5 Net Stretch
The net stretch of a tubular string from its horizontal position at the surface to its
position suspended in a wellbore is the sum of the above factors,
()
() (
δαγ
µγ
γ
γ
L
E
zz
E
zz
E
zz z
T
f
s
f
=+
⎛
⎝
⎜
⎞
⎠
⎟
−+ − − −05
2
2
2
1
2
21
2
22 1
.
)
(9-12)
Note that the stretch is not a function of either the outside diameter or wall
thickness of the tube.
9-4 Casing/Tubing Design Manual
October 2005
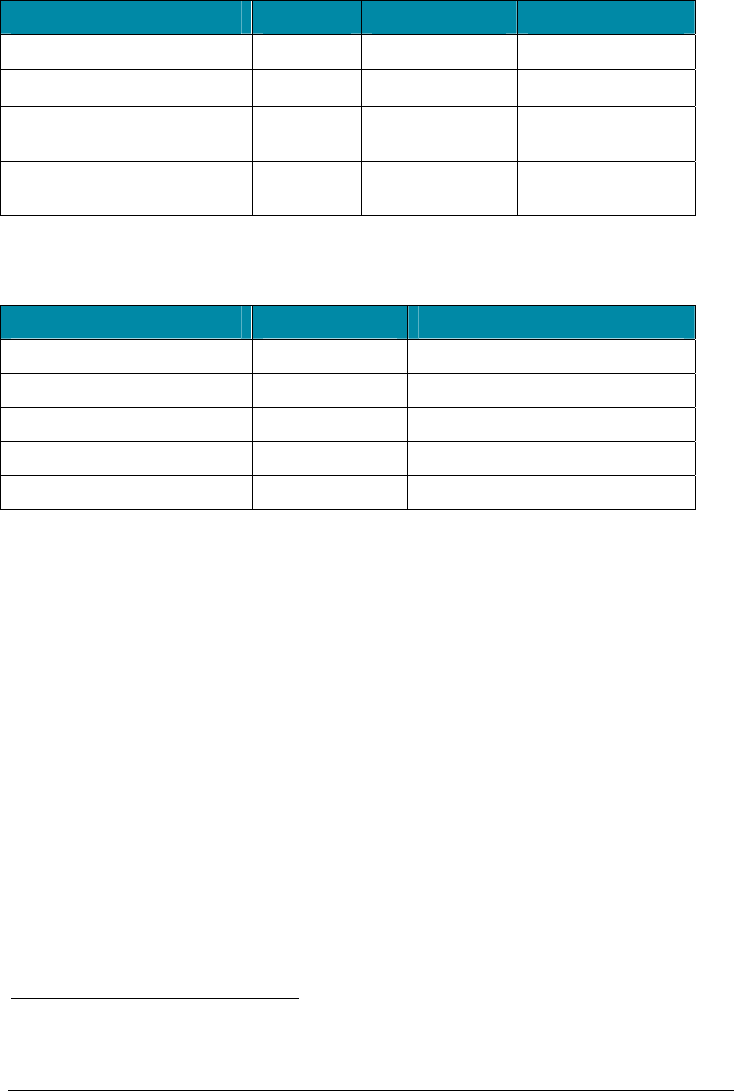
9.2.6 Example Calculation
A steel tubular 1,524-m (5,000 ft.) long, with the material constants shown in
Table 9-2 is run in a wellbore to a depth (
) of 4,542 m (15,000 ft.) as a liner.
The wellbore is full of 1,917-kg/m
z
2
3
(16-ppg) fluid, and has a geothermal gradient
of 2.0°C/100 m (1.1°F/100 ft.).
Table 9-2. Material Constants for Example Stretch Calculation
Constant Symbol Metric English
Young’s modulus
E
2.068x105 MPa 30x106 psi
Poisson’s ratio
µ
0.3 0.3
Coefficient of linear thermal
expansion
α
1.24x10-5 1/°C 6.9x10-6 1/°F
Weight density
γ
s
7842 kgf/m3 or
76,900 N/m3
0.2833 lb/in3
The stretch of the tubular is shown in Table 9-3
1
.
Table 9-3. Results of Example Stretch Calculation
Effect Metric (m) English (ft)
Temperature 1.41 4.74
Ballooning 0.31 1.04
Self weight 0.43 1.42
Hydrostatic end load -0.63 -2.08
Net stretch 1.52 5.12
Note the following:
• The significant contribution from temperature, which is often ignored in
stretch calculations.
• Only the contribution from hydrostatic end load varies with depth.
1
The metric and English calculations will be close, but not identical due to round off in
setting constants and the input variables for the problem.
Casing/Tubing Design Manual 9-5
October 2005

9.3 Stretch in a Vertical Wellbore,
Tapered String
If the tubular string consists of more than one outside diameter or wall thickness,
the procedure for a single string outlined above must be modified slightly.
9.3.1 Lower Segment
Stretch of the lower segment is calculated in a manner identical to that described
in the previous section.
9.3.2 Upper Segment
For the upper segment, the stretch because of temperature, ballooning, and
weight follow from the previous section. The stretch because of end load must be
altered, however. The lower end of the upper segment is subjected to an axial
force consisting of the following contributions:
• The hydrostatic force acting at the lower end of the lower segment. This force
is transmitted through the lower segment and acts at the bottom of the upper
segment.
• The weight of the lower segment.
• A shoulder force generated by hydrostatic pressure acting on the exposed
shoulder at the crossover between the upper and lower segments of the
tubular string. The shoulder may be due to differences in outside diameter,
inside diameter, or both.
Consider the upper segment to be run in the interval
to . Let and be
the outside diameter and wall thickness of the upper segment, respectively. Let
and be the corresponding measures for the lower segment. The shoulder
areas at the crossover are
z
0
z
1
D
u
t
u
D
l
t
l
2
:
()
ADD
so l u
=−
π
4
22
(9-13)
()(
ADtDt
si u u l l
=−−−
⎡
⎣
⎢
⎤
⎦
⎥
π
4
22
22
)
(9-14)
2
Note that both areas are defined such that a positive value for the area produces a tensile
force on the upper segment.
9-6 Casing/Tubing Design Manual
October 2005

Therefore, the hydrostatic force at the crossover is,
(
)
()
[
]
FztDttDt zAA
zfl luuu fl
=−−−
⎡
⎣
⎢
⎤
⎦
⎥
=−
πγ γ
11u
(9-15)
where
and are the cross-sectional areas of the upper and lower
segments, respectively. The total axial force at the bottom of the upper segment
is,
A
u
A
l
(
)
(
)
()
()
FzAzzAzz
zA z z A
zA BFw z z
zfus lf
fus
f
s
l
fu l
=− + − − −
=− + −
⎛
⎝
⎜
⎞
⎠
⎟
−
=− + ⋅ −
γγ γ
γγ
γ
γ
γ
121 21
121
121
1
A
l
(9-16)
where
is the buoyancy factor and is the weight per length of the lower
segment. In other words, the axial force at the lower end of the upper segment
may be rearranged as a hydrostatic force at the bottom of the upper segment as
if the lower segment were absent and the buoyed weight of the lower segment.
The stretch due to this force is:
BF
w
l
()
[
]
(
δγ
L
E
zBFwzzAzz
sh f l u
=− +⋅ − −
1
1211
/
)
0
(9-17)
9.3.3 Example Calculation
Continuing the example from the single-string stretch calculation, assume that
the lower segment is run as part of a tapered long string. The upper segment is
273 mm, 26.7 mm wall (10.750 in., 1.05 in. wall) and the lower segment is 244
mm, 13.8 mm wall (9.625 in., 0.545 in. wall). Assuming the upper segment to
extend from the surface to 3,048 m (10,000 ft.), the stretch calculations for the
lower segment are given by the example for the single string. For the upper
segment, the stretch of the tubular is shown in Table 9-4.
Table 9-4. Results of Stretch Calculation for Tapered String
Effect Metric
(m)
English
(ft)
Temperature 1.15 3.80
Ballooning 0.25 0.83
Self weight 1.73 5.67
Hydrostatic end load -0.21 -0.69
Net stretch 2.92 9.61
Therefore, the total stretch of the tapered string is 1.52 m + 2.92 m = 4.44 m
(5.12 ft + 9.61 ft = 14.73 ft).
Casing/Tubing Design Manual 9-7
October 2005

9.4 Tubing Movement
Consider a tubing string as described in Table 9-5
3
. The tubing is set in a packer
having a bore of 82.55 mm (3.25 in).
The tubing is installed in a completion fluid having a density of 1019 kg/m3 (8.5
ppg). Subsequent operations include a hydraulic fracturing treatment where the
anticipated surface pressure is 34.47 MPa (5,000 psi) with a fracturing fluid
density of 1,378 kg/m3 (11.5 ppg). The temperature of the tubing (assumed to be
the geothermal gradient is 21.1°C (70°F) at the surface with a gradient of
2.19°C/100 m (1.2°F/100 ft). During the fracturing treatment the temperature is
assumed to drop to 10.0°C (50°F) at the surface and 15.6°C (60°F) bottom hole.
3
Notice that the only difference between segments 2 and 3 is the radial clearance change
in the 177.80 mm (7 in.) production casing at 2,156 m (7,000 ft) from 43.16 kg/m (29
ppf) to 47.62 (32 ppf).
9-8 Casing/Tubing Design Manual
October 2005

Table 9-5. Example Tubing String (Top to Bottom)
Segment Attribute Symbol Metric English
1 Length
L
609.6 m 2,000 ft
Outside Diameter
D
88.90 mm 3.5 in
Wall Thickness
t
6.45 mm 0.254 in
Grade (Minimum
Yield Strength)
σ
y
551.6 MPa 80,000 psi
Weight with
Connection
w
s
13.69 kg/m 9.2 lb/ft
Connection Joint
Efficiency
100% 100%
Radial Clearance
r
c
34.09 mm 1.342 in
2 Length
L
1,524.0 m 5,000 ft
Outside Diameter
D
73.03 mm 2.875 in
Wall Thickness
t
5.51 mm 0.217 in
Grade (Minimum
Yield Strength)
σ
y
379.2 MPa 55,000 psi
Weight with
Connection
w
s
9.67 kg/m 6.5 lb/ft
Connection Joint
Efficiency
100% 100%
Radial Clearance
r
c
42.02 mm 1.654 in
3 Length
L
304.8 m 1,000 ft
Outside Diameter
D
73.03 mm 2.875 in
Wall Thickness
t
5.51 mm 0.217 in
Grade (Minimum
Yield Strength)
σ
y
379.2 MPa 55,000 psi
Weight with
Connection
w
s
9.67 kg/m 6.5 lb/ft
Connection Joint
Efficiency
100% 100%
Radial Clearance
r
c
40.88 mm 1.610 in
Determine what length of seals will be necessary to accommodate tubing
movement during the fracturing treatment.
Casing/Tubing Design Manual 9-9
October 2005

9.4.1 Initial Conditions
The initial state of the tubing, immediately following setting of the packer is
summarized in Table 9-6. In completing the table, the following formulas, listed in
the order in which they were used, were applied.
Table 9-6. Conditions Immediately Following Installation
Segment Attribute Symbol Metric English
1 Internal area
A
i
4,536 mm
2
7.031 in
2
External area
A
o
6207 mm
2
9.621 in
2
Moment of inertia
I
1.483x10
6
mm
4
3.432 in
4
Axial force at
bottom
F
z
141.9 kN 31913 lb
Effective force at
bottom
F
e
152.1 kN 34200 lb
Internal pressure
at bottom
p
i
6.092 MPa 883.1 psi
External pressure
at bottom
p
o
6.092 MPa 883.1 psi
Effective weight
w
e
11.99 kg/m 8.06 lb/ft
Average
temperature
T
ave
27.8°C 82°F
2 Internal area
A
i
3,020 mm
2
4.680 in
2
External area
A
o
4,189 mm
2
6.492 in
2
Moment of inertia
I
6.705x10
5
mm
4
1.611 in
4
Axial force at
bottom
F
z
0.415 kN 100 lb
Effective force at
bottom
F
e
25.33 kN 5,701 lb
Internal pressure
at bottom
p
i
21.32 MPa 3,091 psi
External pressure
at bottom
p
o
21.32 MPa 3,091 psi
Effective weight
w
e
8.48 kg/m 5.70 lb/ft
Average
temperature
T
ave
51.1°C 124°F
3 Internal area
A
i
3,020 mm
2
4.680 in
2
External area
A
o
4,189 mm
2
6.492 in
2
Moment of inertia
I
6.705x10
5
mm
4
1.611 in
4
Axial force at
bottom
F
z
-28.49 kN -6,400 lb
9-10 Casing/Tubing Design Manual
October 2005

Segment Attribute Symbol Metric English
Effective force at
bottom
F
e
0 MN 0 lb
Internal pressure
at bottom
p
i
24.37 MPa 3,532 psi
External pressure
at bottom
p
o
24.37 MPa 3,532 psi
Effective weight
w
e
8.48 kg/m 5.7 lb/ft
Average
temperature
T
ave
71.2°C 160°F
In completing Table 9-6, the following formulas, listed in the order in which they
were used, were applied.
9.4.1.1 Internal Area
(
ADt
i
=−
)
π
4
2
2
(9-18)
9.4.1.2 External Area
AD
o
=
π
4
2
(9-19)
9.4.1.3 Moment of Inertia
()
[
]
IDDt=−−
π
64
2
4
4
(9-20)
9.4.1.4 Area of Packer Cross Section
()
APacBor
p
= e
π
4
2
ker
(9-21)
9.4.1.5 Total Length of String
LLLL
TOT i
i
==++L
∑
123
(9-22)
Casing/Tubing Design Manual 9-11
October 2005

9.4.1.6 Internal Pressure at Bottom of Section
k
() () ()
pp
i
k
i
surf
i
j
l
j
k
=+
=
∑
γ
1
L
(9-23)
For the current example the calculation for Section 2 in metric units is:
()
()
px
MN
kg
MPa
i
f
2
6
0 980665 10 1019 6096 1019 1524 2132=+ ⋅ + ⋅ =
−
...
and in English units it is:
()
()
p
psi ft
ppg
psi
i
2
0 0051948 85 2000 85 5000 3091=+ ⋅ + ⋅ =.
/
..
9.4.1.7 External Pressure at Bottom of Section
k
() () ()
pp
o
k
o
surf
o
j
l
j
k
=+
=
∑
γ
1
L
(9-24)
9.4.1.8 Axial Force at Bottom of the Bottom Section
() ()
(
)
(
)
FpAApA
z
TD
i
TD
pi o
TD
po
=− − + −() A
(9-25)
For this example:
()
(
)
(
)
(
)
pppp
i
TD
io
TD
o
==
33
, (9-26)
9.4.1.9 Axial Force at Bottom of the Section
() () ( ) ()() ()
()() ()
FF wL pAA
pA A
z
i
z
j
s
j
i
j
i
j
i
j
o
j
o
j
o
j
=+ + −
⎛
⎝
⎜
⎞
⎠
⎟
−−
⎛
⎝
⎜
⎞
⎠
⎟
++
+
11
1
+1
(9-27)
where
is the section below section
j +1
j
.
For the current example, the calculation for Section 1 in metric units is,
()
()
()
F
N
kg
N
z
f
1
415 980665 9 67 1524 6092 4536 3020
6092 6207 4189 141879
=+ ⋅⋅ + −
−−=−
...
.
and in English units is,
()
(
)
()
F
lb
z
1
10 65 5000 8831 7 031 4 68
8831 9 621 6492 13913
=+⋅ + −
−−=−
...
.. .
.
9-12 Casing/Tubing Design Manual
October 2005
